The Spacetime Surrounding Superconducting Cosmic Strings

Extract

In 1981, A. Vilenkin derived the stress tensor for a straight nonconducting cosmic string of linear mass density μ oriented in the z-direction; it is given by T_μ^ν = μdiag(1,0,0,1) δ (x) δ (y). He also showed that in linear approximation the resulting exterior spacetime is flat but conical, with deficit angle 8πGμ. Subsequently it was shown that even the exact spacetime is flat but conical. Recently E. Copeland, M. Hindmarsh, and N. Turok have derived the stress tensor 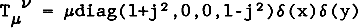for a straight current-carrying string, where j is proportional to the current. We have used this stress tensor, together with the stress tensor of the external electromagnetic field caused by the current, to find the external spacetime of a conducting string in linear approximation. In cylindrical coordinates, the metric may be written 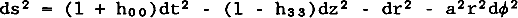where h₀₀ = 4GI²ln²r/r₀ + 8Gμj²lnr/r₀ = h₃₃ + 8GI²lnr/r₀, and a = 1–4Gμ–2GI². Here r₀ is the string radius and I is the electric current, related to j as described in reference 4. The linear approximation is valid as long as h_{0 0} and h_{3 3} are small compared with unity, which restricts the range of r. The (r, φ) subspace is flat but conical, with deficit angle 8πG(μ + I²/2). The spacetime reduces to that found by Vilenkin if j and I go to zero. Efforts are currently underway to find an exact exterior solution, which would apply for arbitrary values of r.