Article contents
Seismic Detection of Boundaries of Stellar Convective Regions
Published online by Cambridge University Press: 08 February 2017
Extract
The edge of a convective region inside a star gives rise to a characteristic periodic signal in the frequencies of its global p-modes (e.g. [1], [4]), such that the frequencies ω are then essentially a smooth function of the mode order n plus a periodic component 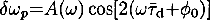 . Here the amplitude is
. Here the amplitude is 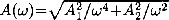 , with A1 and A2 being values that depend weakly on frequency ω: A1 is always present in general, but A2 will be non-zero only if there is overshoot;
, with A1 and A2 being values that depend weakly on frequency ω: A1 is always present in general, but A2 will be non-zero only if there is overshoot; 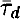 is essentially the acoustical depth τ (i.e. the sound travel time) of the edge of the convection zone measured from the surface of the star; and Φ0 is a constant related to the phase of the eigenfunctions. To facilitate the comparison between different stars, we consider the amplitude evaluated at a fiducial frequency by defining
is essentially the acoustical depth τ (i.e. the sound travel time) of the edge of the convection zone measured from the surface of the star; and Φ0 is a constant related to the phase of the eigenfunctions. To facilitate the comparison between different stars, we consider the amplitude evaluated at a fiducial frequency by defining 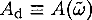 . For the Sun, we chose as the reference frequency
. For the Sun, we chose as the reference frequency 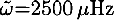 . If we take this value and scale it for other stars (using just a standard homology scaling for frequencies), we find
. If we take this value and scale it for other stars (using just a standard homology scaling for frequencies), we find 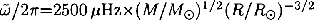 .
.
- Type
- V. Asteroseismology I
- Information
- Symposium - International Astronomical Union , Volume 185: New Eyes to See Inside the Sun and Stars , 1998 , pp. 315 - 316
- Copyright
- Copyright © Kluwer 1998
References
- 1
- Cited by


