Reduction of Sound Speed during Cosmological First Order Phase Transition

Extract

The degree of sound speed reduction is estimated during the coexistence epoch of quark-gluon and hadron phases in the first-order QCD phase transition[1]. The sound speed in a mixture is obtained by simply replacing the energy density with the mean value in the usual formula[2]. Since the adiabatic condition is nothing but the second law of thermodynamics which is useless for the purpose of calculating the sound speed qualitatively, we adopt the conservation of the quality which is the energy fraction of the high-energy phase[2]. This is appropriate because the transition of the phases through bubble nucleation is totally suppressed at the coexistence temperature and the expansion speed of bubbles is so small that energy transfer through bubble expansion or contraction is also expected to be negligible during sound-wave propagation. Using the bag model, the numerical value of the minimum sound speed can be calculated as 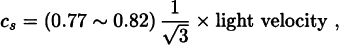where the uncertainty comes from the selection of the number of relativistic quark species. Thus we can say that the quark-hadron phase transition has no drastic effect on the development of cosmological density perturbations.