No CrossRef data available.
Article contents
Origin of Universal Correlation between Temperature and Emision Measure for Solar/Stellar Flares
Published online by Cambridge University Press: 13 May 2016
Extract
We study the reconnection and the chromospheric evaporation in flares using the numerical code including nonlinear anisotropic heat conduction effect (Yokoyama & Shibata 1998; 2001). The two-dimensional, nonlinear, timedependent, resistive, compressible MHD equations are solved. The evolution from the rise phase to (the early part of) the decay phase of a solar flare is qualitatively reproduced in this simulation. Based on the results, we obtained a relationship between the flare temperature and the coronal magnetic field strength. If we assume that the input of energy to a loop balances with the conduction cooling rate, the temperature at the loop apex is TA ≈ (2QL2/κ0)2/7 where Q is the volumetric heating rate, L is the half-length of the loop, and κ0 = 10−6 eGS is the Spitzer's thermal conductivity constant. In our simulations, the heating mechanism is magnetic reconnection so that the heating rate is described as Q = B2/(4π) · Vin/L · 1/sin θ, where B is the coronal magnetic field strength, Vin is the inflow velocity (≈ 0.1VA from our result and also from Petschek's theory), and θ is the angle between the slow-mode MHD shock and the loop and is approximately given by sin θ ≈ Vin/VA. By manipulating the equations, we find
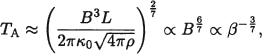 where ρ is the mass density of the corona. The simulation results show very good agreement with this scaling law.
where ρ is the mass density of the corona. The simulation results show very good agreement with this scaling law.
- Type
- Session III: Active Region Structure and Dynamics
- Information
- Copyright
- Copyright © Astronomical Society of the Pacific 2001


