On rotating ring orbits in galaxies

Extract

If ω is the angular velocity of circular motions in a stellar system depending on the distance R from the centre, and κ is the frequency of oscillation in the radius vector for an orbit in the equatorial plane which differs slightly from a circular orbit, we may show that in a coordinate system of angular speed 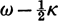the orbit in question is a closed oval, in the first approximation an ellipse, with two opposite vertices and with its centre in the centre of the system. The conditions are illustrated in Fig. 1, when AA is the apsidal line of an orbit. The expression for κ is 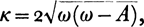where A is Oort's constant of differential rotation. If the distribution of matter in the stellar system may be approximated by a sum of concentric spheroids with one and the same plane of symmetry, the density increasing with decreasing dimensions of the spheroids, we should expect κ = 2ω close to the centre, whereas in the outermost regions we must expect that κ approaches to ω. It is therefore likely that ω – ½κ does not change appreciably within the system. Fig. 2 gives the run of κ, ω, and ω – ½κ for the galactic system according to the values of ω given by Kwee, Muller, and Westerhout [2]. In this case ω – ½κ changes very slowly with R. A relative orbit has a quite important property, if ω – ½κ is constant in the interval of R covered by the orbit. In this case, if the centre of gravity of a cloud of free particles follows the orbit, and if the velocity dispersion is small, the particles will pursue orbits which differ only slightly from each other and from the central orbit, but on the other hand there will in general be considerable differential motions along the central orbit. This orbit is therefore the curve in space along which a cloud of free particles tends to disperse. The process is similar to the dispersion of the meteoric particles of a comet along its orbit.