Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T04:48:51.307Z Has data issue: false hasContentIssue false
  • English
  • Français

Determinations of Distances to Radio Sources with VLBI

Published online by Cambridge University Press:  03 August 2017

Norbert Bartel
Norbert Bartel*
Affiliation:
Harvard-Smithsonian Center for Astrophysics

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The most direct method of determining distances to galactic sources outside the Solar System is the measurement of annual parallaxes. Using as an example astrometric observations of the quasars 3C345 and NRAO512 which are separated by ∼ 0°.5 at the sky, we show that under certain conditions, annual parallaxes of galactic radio sources can be determined with VLBI with an accuracy of 50 μas (standard error). This accuracy is about tenfold higher than any annual parallax accuracy ever obtained with optical astrometry.

The, so far, most direct method of determining distances to extragalactic sources combines VLBI measurements of a supernova's angular expansion velocity with optical spectroscopic measurements of the supernova's radial expansion velocity. We have estimated the distance to SN1979C in M100 in the Virgo cluster to be 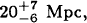a lower bound on the distance to SN1980K in NGC6946 to be 5 Mpc, and H0 to be 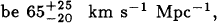with the uncertainties intended to represent standard errors.

Type
Extragalactic
Information
Symposium - International Astronomical Union , Volume 129: The Impact of VLBI on Astrophysics and Geophysics , 1988 , pp. 175 - 184
Copyright
Copyright © Reidel 1988 

References

Aaronson, M. et al. 1982, Ap. J. Suppl., 50, 241.CrossRefGoogle Scholar
Allen, R. J., Baldwin, J. E. and Sancisi, R. 1978, Astr. Ap., 62, 397.Google Scholar
Bartel, N. 1985, in Supernovae as Distance Indicators, Lecture Notes in Physics , ed. Bartel, N. (Springer-Verlag, Berlin), 224, 107.Google Scholar
Bartel, N. 1986, in Highlights of Astronomy, ed. Swings, J. P., 7, 655.Google Scholar
Bartel, N., Herring, T. A., Ratner, M. I., Shapiro, I. I., and Corey, B. E. 1986, Nature, 319, 733.Google Scholar
Bartel, N., Rogers, A. E. E., Shapiro, I. I., Gorenstein, M. V., Gwinn, C. R., Marcaide, J. M., and Weiler, R. W. 1985, Nature, 318, 25.Google Scholar
Bartel, N., Rupen, M., and Shapiro, I. 1987, IAU Circ. 4292.Google Scholar
Branch, D., Falk, S. W., McCall, M. L., Rybski, P., Uomoto, A., and Wills, B. J. 1981, Ap. J., 244, 780.CrossRefGoogle Scholar
de Vaucouleurs, G. 1979, Ap. J., 227, 380.CrossRefGoogle Scholar
de Vaucouleurs, G. 1982, Ap. J., 253, 520.CrossRefGoogle Scholar
Green, D. A. 1984, M. N. R. A. S., 209, 449.Google Scholar
Gwinn, C. R., Taylor, J. H., Weisberg, J. M., and Rawley, L. A. 1986, A. J., 91, 338.CrossRefGoogle Scholar
Lestrade, J.- F. 1988, this volume.Google Scholar
Marscher, A. P. 1985, in Supernovae as Distance Indicators, Lecture Notes in Physics , ed. Bartel, N. (Springer-Verlag, Berlin), 224, 130.Google Scholar
Monet, D. G., Dahn, C. C., Harris, H. C., Ables, H. D., Luginbuhl, C. B., Pier, J. R., and Vrba, F. J. 1987, Bull. AAS, 19, 79.09.Google Scholar
Reid, M. J. 1988, this volume.Google Scholar
Rupen, M. P., van Gorkom, J. H., Knapp, G. R., Gunn, J. E., and Schneider, D. P. 1987 A. J., 94, 61.Google Scholar
Sandage, A., and Tammann, G. H. 1974, Ap. J., 194, 559.Google Scholar
Sandage, A., and Tammann, G. H. 1985, in Supernovae as Distance Indicators, Lecture Notes in Physics, ed. Bartel, N. (Springer-Verlag, Berlin), 224, 1.Google Scholar
Shapiro, I. I. et al. 1979, A. J., 84, 1459.Google Scholar
Shapiro, I. I. et al. 1988, this volume.Google Scholar
Uomoto, A., and Kirshner, R. P. 1986, Ap. J., 308, 685.Google Scholar
Weiler, K. W., Sramek, R. A., Panagia, N., van der Hulst, J. M., and Salvati, M. 1986, Ap. J., 301, 790.Google Scholar
Wittels, J. J. et al. 1976, A. J., 81, 933.Google Scholar