Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-13T00:59:41.973Z Has data issue: false hasContentIssue false
  • English
  • Français

Convection and its Stability in the Equatorial Regions of the Convection Zone

Published online by Cambridge University Press:  08 February 2017

A.V. Klyachkin
A.V. Klyachkin*
Affiliation:
Ioffe Physical- Technical Institute Academy of Sciences Ul. Politechnicheskaya 26 194021, Leningrad, USSR

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The problem of the existence, evolution, and stability of spatial structures in convection is of considerable importance to astrophysics as well as to geophysical hydrodynamics. The Boussinesq approximation will be used because the considered motions in stars are sufficiently slow. The system of hydrodynamic equations describing convection in a rotating inhomogeneous medium has the form: 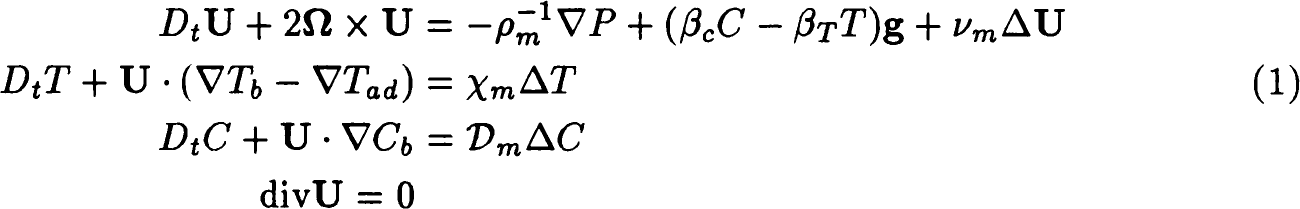Here Dt is the total time derivative, U the velocity, P, T, and C the deviations of the pressure, temperature, and helium abundance (by mass) from the basic equilibrium values, ρm, νm, χm, and Dm the values averaged over the considered layer of the density, viscosity, thermal and helium diffusivities, βT and βc the averaged coefficients of the thermal and helium expansions, g and Ω the gravitational acceleration and angular velocity, ∇Tb, and ∇Cb the values of the basic equilibrium temperature and helium gradients, and ñTad the adiabatic temperature gradient.

Type
V. Large-scale Structure and Dynamics
Information
Symposium - International Astronomical Union , Volume 138: Solar Photosphere: Structure, Convection and Magnetic Fields , 1990 , pp. 325 - 328
Copyright
Copyright © Kluwer 1990 

References

DiPrima, R.C., Eckhaus, W., and Segel, L.A. (1971) ‘Non-linear wave-number interaction in near-critical two-dimensional flows’, J. Fluid Mech. 49, 705–744.CrossRefGoogle Scholar
Doering, C.R., Gibbon, J.D., Holm, D.D., and Nicolaenko, B. (1988) ‘Low-dimensional behaviour in the complex Ginzburg-Landau equation’, Nonlinearity 1, 279–309.CrossRefGoogle Scholar
Dolginov, A.Z. and Klyachkin, A.V. (1987) ‘The influence of the helium abundance on the convection threshold in surface layers of rotating stars’, Piz'ma v Astronomicheskii Zhurnal 13, 764–772.Google Scholar
Dolginov, A.Z. and Klyachkin, A.V. (1988) ‘Influence of the chemical composition on the convection, meridional circulation and differential stellar rotation’, in Glagolevsky, Yu.V. and Kopylov, J.M. (eds.), Magnetic Stars , “Nauka”, Leningrad, pp. 264–280.Google Scholar
Dolginov, A.Z. and Klyachkin, A.V. (1989) ‘Convection in the equatorial region of a rotating chemically nonuniform star’, Piz'ma v Astronomicheskii Zhurnal 15, 33–41.Google Scholar
Durney, B. (1970) ‘Nonaxisymmetrical convection in a rotating spherical shell’, Astrophys. J. 161, 353–367.CrossRefGoogle Scholar
Klyachkin, A.V. (1989) ‘The modulation of the autowave convective structures on the rotating chemically nonuniform stars’, Preprint No. 1338, Physical-Technical Ioffe Institute, Leningrad.Google Scholar
Landau, L.D. and Lifshits, E.M. (1986) Gidrodinamika , “Nauka”, Moscow.Google Scholar