Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-12-04T09:58:45.577Z Has data issue: false hasContentIssue false
  • English
  • Français

Sample size for detecting and estimating the proportion of transgenic plants with narrow confidence intervals

Published online by Cambridge University Press:  03 March 2010

Osval Antonio Montesinos López ,
Abelardo Montesinos López ,
José Crossa ,
Kent Eskridge  and
Carlos Moises Hernández Suárez
Osval Antonio Montesinos López
Affiliation:
Facultad de Telemática, Universidad de Colima, Bernal Díaz del Castillo No. 340 Col. Villa de San Sebastián, C.P. 28045Colima, Colima, México
Abelardo Montesinos López
Affiliation:
Departamento de Estadística. División de Ciencias Forestales, Universidad Autónoma Chapingo, Texcoco, Estado de México, México
José Crossa*
Affiliation:
Biometrics and Statistics Unit of the Crop Research Informatics Laboratory (CRIL) of the Maize and Wheat Improvement Center (CIMMYT), Apdo. Postal 6-641, México DF, México
Kent Eskridge
Affiliation:
Department of Statistics, University of Nebraska, Lincoln, Nebraska, USA
Carlos Moises Hernández Suárez
Affiliation:
Facultad de Ciencias, Universidad de Colima, Bernal Díaz del Castillo No. 340 Col. Villa de San Sebastián, C.P. 28045Colima, Colima, México
*
*Correspondence Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Detecting the presence of genetically modified plants (adventitious presence of unwanted transgenic plants, AP) from outcrossing species such as maize requires a method that lowers laboratory costs without losing precision. Group testing is a procedure in which groups that contain several units (plants) are analysed without having to inspect individual plants, with the purpose of estimating the prevalence of AP in a population at a low cost without losing precision. When pool (group) testing is used to estimate the prevalence of AP (p), there are sampling procedures for calculating a confidence interval (CI); however, they usually do not ensure precision in the estimation of p. This research proposes a method to determine the number of pools (g), given a pool size (k), that ensures precision in the estimated proportion of AP (that is, it ensures a narrow CI). In addition, the study computes the maximum likelihood estimator of p under pool testing and its exact CI, considering the detection limit of the laboratory, d, and the concentration of AP per unit (c). The proposed sample procedure involves two steps: (1) obtain a sample size that guarantees that the mean width of the CI (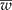) is narrower than the desired width (ω); and (2) iteratively increase the sample size until 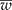is smaller than the desired width (ω) with a specified degree of certainty (γ). Simulated data were created and tables are presented showing the different possible scenarios that a researcher may encounter. An R program is given and explained that will reproduce the results and make it easy for the researcher to create other scenarios.

Keywords

adventitious presence of transgenic plantsconfidence intervalconfidence interval widthpool sampling
Type
Research Article
Information
Seed Science Research , Volume 20 , Issue 2 , June 2010 , pp. 123 - 136
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bhattacharyya, G.K., Karandinos, M.G. and DeFoliart, G.R. (1979) Point estimates and CIs for infection rates using pooled organisms in epidemiologic studies. American Journal of Epidemiology 109, 124–131.CrossRefGoogle Scholar
Bilder, C.R. (2007) Human or Cylon? Group testing on the Battlestar Galactica, Invited seminar, 5 October 2007, Department of Statistics, University of Missouri, Columbia, Missouri.Google Scholar
Burrows, P.M. (1987) Improved estimation of pathogen transmission rates by group testing. Phytopathology 77, 363–365.CrossRefGoogle Scholar
Cesana, B.M., Reina, G.E. and Marubini, E. (2001) Sample size for testing a proportion in clinical trials: a ‘two-step’ procedure combining power and CI expected width. The American Statistician 55, 288–292.Google Scholar
Chiang, C.L. and Reeves, W.C. (1962) Statistical estimation of virus infection rates in mosquito vector populations. American Journal of Hygiene 75, 377–391.Google Scholar
Christianson, J., McPherson, M., Topinka, D., Hall, L. and Good, A.G. (2008) Detecting and quantifying the adventitious presence of transgenic seeds in safflower, Carthamus tinctorius L. Journal of Agricultural and Food Chemistry 56, 5506–5513.Google Scholar
Cleveland, D.A., Soleri, D., Aragón-Cuevas, F., Crossa, J. and Gepts, P. (2005) Detecting (trans)gene flow to landraces in centers of crop origin: lessons from the case of maize in Mexico. Environmental Biosafety Research 4, 197–208.Google Scholar
Cohen, J. (1988) Statistical power analysis for the behavioral sciences (2nd edition). Hillsdale, New Jersey, Erlbaum.Google Scholar
Cohen, J. (1994) The earth is round (p < 0.05). American Psychologist 49, 997–1003.CrossRefGoogle Scholar
Dorfman, R. (1943) The detection of defective members of large populations. The Annals of Mathematical Statistics 14, 436–440.Google Scholar
Dyer, G.A., Serratos-Hernández, J.A., Perales, H.R., Gepts, P., Piñeyro-Nelson, A., Chavez, A., Salinas-Arreortua, N., Yúnez-Naude, A., Taylor, J.E. and Alvarez-Buylla, E.R. (2009) Dispersal of transgenes through maize seed systems in Mexico. PLoS ONE 4, e5734.Google Scholar
Federer, W. (1991) Statistics and society. Data collection and interpretation. New York, Marcel and Dekker.Google Scholar
Feller, W. (1957) An introduction to probability theory and its applications, Vol. 1 (2nd edition). New York, Wiley.Google Scholar
Hahn, G. and Meeker, W. (1991) Statistical intervals: a guide for practitioners. New York, Wiley.Google Scholar
Hepworth, G. (1996) Exact CIs for proportions estimated by group testing. Biometrics 52, 1134–1146.Google Scholar
Hernández-Suárez, C.M., Montesinos-López, O.A., McLaren, G. and Crossa, J. (2008) Probability models for detecting transgenic plants. Seed Science Research 18, 77–89.Google Scholar
Hughes, G. and Gottwald, T.R. (1998) Survey methods for assessment of citrus tristeza virus incidence. Phytopathology 88, 715–723.Google Scholar
Katholi, C.R. and Unnasch, T.R. (2006) Important experimental parameters for determining infection rates in arthropod vectors using pool screening approaches. American Journal of Tropical Medical Hygiene 74, 779–785.Google Scholar
Kelley, K. (2007a) Sample size planning for the coefficient of variation from the accuracy in parameter estimation approach. Behavior Research Methods 39, 755–766.Google Scholar
Kelley, K. (2007b) Methods for the Behavioral, Educational and Social Sciences (MBESS) [computer software and manual]. Available atwww.cran.r-project.org/ (accessed 1 February 2010).Google Scholar
Kelley, K. (2007c) CIs for standardized effect sizes: theory, application and implementation. Journal of Statistical Software 20, 1–24.Google Scholar
Kelley, K. and Maxwell, S.E. (2003) Sample size for multiple regression: obtaining regression coefficients that are accurate, not simply significant. Psychological Methods 8, 305–321.Google Scholar
Kelley, K. and Rausch, J.R. (2006) Sample size planning for the standardized mean difference: accuracy in parameter estimation via narrow confidence intervals. Psychological Methods 11, 363–385.Google Scholar
Kelley, K., Maxwell, S.E. and Rausch, J.R. (2003) Obtaining power or obtaining precision: Delineating methods of sample size planning. Evaluation & the Health Professions 26, 258–287.Google Scholar
Kendziorski, C., Irizarry, R.A., Chen, K.S., Haag, J.D. and Gould, M.N. (2005) On the utility of pooling biological samples in microarray experiments. Proceedings of the National Academy of Sciences, USA 102, 4252–4257.CrossRefGoogle ScholarPubMed
Kline, R.L., Brothers, T.A., Brookmayer, R., Zeger, S. and Quinn, T.C. (1989) Evaluation of human immunodeficiency virus seroprevalence surveys using pooled sera. Journal of Clinical Microbiology 27, 1449–1452.Google Scholar
Kraemer, H.C.andThiemann, S. (1987) How many subjects? Statistical power analysis in research. Newbury Park, California, Sage.Google Scholar
Kupper, L.L.andHafner, K.B. (1989) How appropriate are popular sample size formulas? The American Statistician 43, 101–105.Google Scholar
Laffont, J.L., Remund, K., Wright, D., Simpson, R.D. and Gregoire, S. (2005) Testing for adventitious presence of transgenic material in conventional seed or grain lots using quantitative laboratory methods: statistical procedures and their implementation. Seed Science Research 15, 197–204.CrossRefGoogle Scholar
Lindan, C., Mathur, M., Kumta, S., Jerajani, H., Gogate, A., Schachter, J. and Moncada, J. (2005) Utility of pooled urine specimens for detection of Chlamydia trachomatis and Neisseria gonorrhoeae in men attending public sexually transmitted infection clinics in Mumbai, India, by PCR. Journal of Clinical Microbiology 43, 1674–1677.CrossRefGoogle ScholarPubMed
Lipsey, M.W. (1990) Design sensitivity: statistical power for experimental research. Newbury Park, California, Sage.Google Scholar
Mace, A.E. (1964) Sample size determination. New York, Reinhold.Google Scholar
Montgomery, D.C. (1997) Introduction to statistical quality control (3rd edition). New York, John Wiley.Google Scholar
Murphy, K.R. and Myors, B. (1998) Statistical power analysis: a simple and general model for traditional and modern hypothesis tests. Mahwah, New Jersey, Erlbaum.Google Scholar
Newcombe, R.G. (1998) Two-sided CIs for the single proportion: comparison of seven methods. Statistics in Medicine 17, 857–872.Google Scholar
Ortiz-García, S., Ezcurra, E., Schoel, B., Acevedo, F., Soberón, J. and Snow, A.A. (2005a) Absence of detectable transgenes in local landraces of maize in Oaxaca, Mexico (2003–2004). Proceedings of the National Academy of Sciences, USA 102, 12338–12343.Google Scholar
Ortiz-García, S., Ezcurra, E., Schoel, B., Acevedo, F., Soberón, J. and Snow, A.A. (2005b) Correction. Proceedings of the National Academy of Sciences, USA 102, 18242.Google Scholar
Ortiz-García, S., Ezcurra, E., Schoel, B., Acevedo, F., Soberón, J. and Snow, A.A. (2005c) Reply to Cleveland et al.'s ‘Detecting (trans)gene flow to landraces in centers of crop origin: lessons from the case of maize in Mexico’. Environmental and Biosafety Research 4, 209–215.Google Scholar
Piñeyro-Nelson, A., van Heerwaarden, J., Perales, H.R., Serratos-Hernández, J.A., Rangel, A., Hufford, M.B., Gepts, P., Garay-Arroyo, A., Rivera-Bustamante, R. and Álvarez-Buylla, E.R. (2009) Transgenes in Mexican maize: molecular evidence and methodological considerations for GMO detection in landrace populations. MolecularEcology 18, 750–761.Google Scholar
Quist, D. and Chapela, I.H. (2001) Transgenic DNA introgressed into traditional maize landraces in Oaxaca, Mexico. Nature 414, 541–543.Google Scholar
Quist, D. and Chapela, I.H. (2002) Quist and Chapela reply. Nature 416, 602.Google Scholar
R Development Core Team (2007) R: A language and environment for statistical computing [computer software and manual]. R Foundation for Statistical Computing. Available atwww.r-project.org (accessed 1 February 2010).Google Scholar
Remund, K.M., Dixon, D.A., Wright, D.L. and Holden, L.R. (2001) Statistical considerations in seed purity testing for transgenic traits. Seed Science Research 11, 101–120.Google Scholar
Romanow, L.R., Moyer, J.W. and Kennedy, G.G. (1986) Alteration of efficiencies of acquisition and inoculation of watermelon mosaic virus 2 by plant resistance to the virus and to an aphid vector. Phytopathology 76, 1276–1281.CrossRefGoogle Scholar
Shah, D.A., Dillard, H.R. and Nault, B.A. (2005) Sampling for the incidence of aphid-transmitted viruses in snap bean. Phytopathology 95, 1405–1411.Google Scholar
Swallow, W.H. (1985) Group testing for estimating infection rates and probabilities of disease transmission. Phytopathology 75, 882–889.Google Scholar
Swallow, W.H. (1987) Relative mean squared error and cost considerations in choosing group size for group testing to estimate infection rates and probabilities of disease transmission. Phytopathology 77, 1376–1381.Google Scholar
Tebbs, J.M. and Bilder, C.R. (2004) Confidence intervals procedures for probability of disease transmission in Multiple-Vector-Transfer designs. Journal of Agricultural, Biological, and Environmental Statistics 9, 79–90.CrossRefGoogle Scholar
Thompson, K.H. (1962) Estimation of the proportion of vectors in a natural population of insects. Biometrics 18, 568–578.Google Scholar
Vollset, S.E. (1993) CIs for a binomial proportion. Statistics in Medicine 12, 809–824.Google Scholar
Watson, M.A. (1936) Factors affecting the amount of infection obtained by aphis transmission of the virus Hy. III. Philosophical Transactions of the Royal Society of London, Series B 226, 457–489.Google Scholar
Williams, C.J. and Moffitt, C.M. (2001) A critique of methods of sampling and reporting pathogens in populations of fish. Journal of Aquatic Animal Health 13, 300–309.2.0.CO;2>CrossRefGoogle Scholar
Yamamura, K. and Hino, A. (2007) Estimation of the proportion of defective units by using group testing under the existence of a threshold of detection. Communications in Statistics – Simulation and Computation 36, 949–957.Google Scholar
Zenios, S.A. and Wein, L.M. (1998) Pooled testing for HIV prevalence estimation: exploiting the dilution effect. Statistics in Medicine 17, 1447–1467.3.0.CO;2-K>CrossRefGoogle ScholarPubMed