Information, meaning and physics: The intellectual evolution of the English School of Information Theory during 1946-1956

Argument

In this comparative historical analysis, we will analyze the intellectual tendency that emerged between 1946 and 1956 to take advantage of the popularity of communication theory to develop a kind of informational epistemology of statistical mechanics. We will argue that this tendency results from a historical confluence in the early 1950s of certain theoretical claims of the so-called English School of Information Theory, championed by authors such as Gabor (1956) or MacKay (1969), and from the attempt to extend the profound success of Shannon’s ([1948] 1993) technical theory of sign transmission to the field of statistical thermal physics. As a paradigmatic example of this tendency, we will evaluate the intellectual work of Léon Brillouin (1956), who, in the mid-fifties, developed an information theoretical approach to statistical mechanical physics based on a concept of information linked to the knowledge of the observer.

1. Introduction

When we talk about information theory, we usually assume that we are referring to the famous Shannon theory. However, prior to the popularization of the theory of signal transmission developed by this American engineer-mathematician in the early 1950s, several scientists in England, such as Nobel Laureate Dennis Gabor (1946), had already independently developed information theories, all of which focused on interdisciplinary analysis of how scientists acquired knowledge through various practices, in contrast to Shannon’s theory which focused technically on signal transmission. In the words of Colin Chery: “This wider field, which has been studied in particular by MacKay, Gabor, and Brillouin, as an aspect of scientific method, is referred to, at least in Britain, as information theory, a term which is unfortunately used elsewhere synonymously with communication theory” (Cherry 1957, 216). This intellectual tendency shaped what McCulloch called the “English School” or what Bar-Hillel called the “European School” of information theory, a current of scientific thought long neglected in the history of science (with some exceptions, see Kline [2015]) and undoubtedly deeply forgotten by the philosophy of physics, in spite of its key role in the formation of this trend of thought in the 1950s. ¹

In this paper we present a comparative analysis of how the so-called English school of information theory evolved, from its emergence in the 1940s to its covert assimilation into the intellectual realm of Shannon’s communication theory during the 1950s. Using an interdisciplinary historiographical and philosophical methodology (what is known in the literature as “history and philosophy of science,” or “HPS”), we will assess how the main goals and theoretical concepts of each school of information theory evolved in contact with the others, defending how the English school ended up subsumed into Shannon’s bandwagon during the years following the publication of his theory. Our central thesis will not be historiographical but properly conceptual: namely, that the constitutive intellectual pretensions of the English school (mainly, clarifying scientific measurement) did not disappear during the 1950s, but changed their conceptual vehicles. As an example of this intellectual trend, we will analyze in detail the conceptual foundation of the information-theoretic proposal that the physicists Jerome Rothstein (1951) and Léon Brillouin (1956) developed in the 1950s, focusing philosophically on the plausible relationship between the notion of information and scientific measurement. In this direction, our argument aims to complement the historical-conceptual analysis of informational trends in twentieth century physics proposed by Jerome Segal in his monumental work “Le zero et le un” (Segal 2003), by focusing exhaustively on the assessment of how the English School was intellectually transformed during the 1950s.

The plan for this paper is the following. In the next section, we will analyze the so-called English school of information theory, which was highly creative and focused on illuminating scientific practices. Section 3 is devoted to describing the basic elements of Shannon’s famous mathematical theory of communication ([1948] 1993). We will then explore the socio-historical context (the so-called London Symposium on Information Theory) in which the English school came into contact in the early 1950s with the sphere of influence of Shannon’s theory. In Section 5 we will evaluate how, in this era, the tendency to apply communication theory to explain the epistemic dynamics of scientific measurement emerged, as was the case with Rothstein (1951). Finally, we will analyze in detail the intellectual work of Brillouin (1956) in his work Science and Information Theory, which represents a paradigmatic example of how the fundamental aims of the English intellectual tradition ended up being historically assimilated by the bandwagon of Shannon’s theory.

2. The English school of information theory

Before the publication of the all-pervasive paper in which Shannon’s mathematical theory of communication was first presented in 1948, on the other side of the Atlantic (specifically in England) there were already several theoretical proposals dealing with certain notions of information. One of the oldest was developed by the British statistician Ronal Fisher, who proposed, in his “Probability, Likelihood and Quantity of Information in the Logic of Uncertain Inference” (Fisher 1934), a measure of the amount of information that a random observable variable X possesses on a parameter O as the reciprocal value of the variance of X with respect to O. Therefore, for Fisher, this statistical technical measure would be called “information” (although the author is not explicit on this point) because of its similarity with the ordinary sense of the term, so that O would provide information about X.

Another theory was put forth by the Hungarian-British physicist Dennis Gabor, from Imperial College, London (winner of the Nobel Prize in 1971 for his invention of holography). In his 1946 paper entitled “Theory of Communication” (anticipating by several years the classical works of Shannon and Wiener), Gabor developed a pioneering information theory closely based on the mathematical apparatus used in physical practices, such as waveform analysis or Fourier-transform theory. Instead of starting from the statistical analysis of signal transmission processes à la Shannon, Gabor starts from the context of communication engineering and the strictly physical domain of the analysis of the frequency-time of the signals that make up the waves. The singularity of his proposal is that not only the communicative processes but also the scientific practices (i.e. measurement or observation activities) could be understood as processes of information acquisition about the analyzed physical phenomena. Assuming these premises, Gabor interpreted as the minimum unit of information (which he called a “logon”) transmitted by a wave signal the amount ΔfΔt = ½, which is the diagonal of the elementary area in the wave’s phase space ΔfΔt.

These preliminary information theoretical works by Fisher (1934) and Gabor (1946), although significantly different from one another, were assimilated in the late 1940s by the young King’s College researcher Donald MacKay, who would then in the 1950s go on to promote what would later become known as the English School of Information Theory. From his early interest in the problem of the limits of scientific measurement, arguing that “the art of physical measurement seemed to be ultimately a matter of compromise, of choosing between reciprocally related uncertainties” (MacKay 1969, 1), this author would evolve intellectually towards the arena of how we should quantify and understand information as it appears naturally in the context of scientific measurement practices. In this way, MacKay’s information theory would not be detached from particular physical theories as in the case of Shannon’s proposal, but would emerge naturally from (or be already incorporated in) from the physical theory itself employed by the agent-observer to obtain significant knowledge through scientific measurement processes.

As in the case of Gabor, scientific measurements themselves are assumed to be contexts for obtaining and processing information about target phenomena. Therefore, we argue at this point that the theoretical pretension of using informational concepts to clarify scientific measurement processes constitutes precisely the defining positive feature of the English school as opposed to the American school, which focused instead on statistically assessing signal-transmission processes. Interestingly, this intellectual tradition of formally evaluating scientific measurements (i) goes back before the English school to the representational theory of measurement developed by Helmholtz in the 19th century, and (ii) tracks forward subsequently through the Bayesian and model-theoretic analyses of the last third of the twentieth century ² (Diez 1997).

First presented at the first London Symposium on Information Theory in 1950, MacKay’s ambitious theory incorporated (i) Fisher’s concept of statistical information encoded by a variable or “metric information” (under the new name of “metron”), and (ii) Gabor’s concept of structural or physical information based on minimum units of phase-frequency-time volume or “logon”. Both information measures encompass what MacKay called “scientific information” due to their role in being used by observers or scientific agents to describe the phenomena observed through certain measurement processes (see Figure 1). Therefore, MacKay argued that all these informational concepts possess, unlike Shannon’s ([1948] 1993) statistical notion, a semantic character derived from the intentionality of these agent-observers: “It appears from our investigations that the theory of information has a natural, precise and objectively definable place for the concept of meaning” (MacKay 1969, 93).

Figure 1. MacKay’s (1969) “scientific information” is defined within a representational space. This representational space could correspond to a volume (grey-colored) in phase space, representing information about the position (P) and velocity (Q) of a molecular system. This vector-description of a molecular encodes MacKay’s “scientific information” (or equivalently, Gabor’s “structural information”), and its vector-orientation its meaning. According to the procedural rules of vector calculus, the meaning of the vector-description* (its semantic information) after performing a scientific measurement on the molecular system would be the opposite of meaning of the previous vector-description. This, as MacKay argued, precisely means that the meaningful information that an agent has about the molecular system increases after that measurement (MacKay 1969, 93).

In addition to integrating Fisher and Gabor’s two English proto-information theories his unifying proposal ³ , MacKay also sought to include the statistical concept of information developed by Shannon, reformulating it as a measure of “selective information”. Therefore, MacKay’s (1969) general definition of information is nothing but a manifold combination of Fisher’s, Gabor’s and Shannon’s definitions, all qualitatively interpreted from the ordinary (semantic and agent-based) sense of information. In this direction, MacKay sought to develop an extremely ambitious unified theory of information based on the scientific practices and theoretical-descriptive resources of the physical sciences, which would encompass not only the proposals of his compatriots Fisher and Gabor, but also Shannon’s popular proposal. Unfortunately, his information theory was at first eclipsed by Shannon’s, and later forgotten by the scientific community in the 1950s, until finally being published two decades later in his 1969 book Information, Mechanism and Meaning.

The last of the main members of the English school of information theory was the electrical engineer Colin Cherry, who would be remembered later for both his theoretical-communicative analysis of the so-called “cocktail party problem” and his 1957 “On Human Communication”. The cocktail party problem refers to the ability of an agent to discriminate a conversation within a noisy room, concluding that the physical properties of the conversation (e.g., the volume at which it was broadcast) were more decisive than its possible semantic characteristics (e.g., the meaning of the phrases it contained) for the assimilation of that conversation. However, his main contribution was undoubtedly the formation of an international community of information scientists through the organization of several symposia during the 1950s, which centered around Shannon’s information theory, but also showcase the existence of alternative theoretical proposals. In this sense, Cherry distinguished between information theories focused on the problem of scientific measurement, emphasized by the English school of Gabor (1946) and MacKay (1969), and those focused on communication engineering, championed on the other hand by Hartley (1928) and Shannon ([1948] 1993). Henceforth, we will use the expression “English school” not to classify the different proposals geographically, but to conceptually identify proposals (British or otherwise) that are determined by their intellectual objective of clarifying the epistemic dynamics underlying scientific measurements.

3. Shannon’s theory and the American school

As is well known, the founding event of information theory (both in general and for the American school in particular) was the publication of “A Mathematical Theory of Information” by Bell Labs worker Claude Shannon ([1948] 1993). In this article, Shannon first set out the foundations of his theoretical proposal (developed technically and conceptually throughout the 1940s) about the information generated during the transmission of signals within communicative contexts made up of (i) a source, which selects the message or sequence of signs within the set of possible messages that can be constructed from a particular alphabet; (ii) a transmitter that encodes the message, converting it into a signal that can be transmitted through a communicative channel with or without noise; (iii) a receiver that decodes the signal (made up of the message and the noise) in order to transfer the message to the destination (see Figure 2).

Figure 2. Shannon’s ([1948] 1993) diagram of a communication model of signal transmission.

One of Shannon’s most popular achievements within the information theoretical community was his Fundamental Theorem for a Discrete Noise Channel. This theorem establishes that the most optimal message coding for transmitting signals over noisy communication channels with “an arbitrarily small frequency of errors” (Shannon [1948] 1993, 411) would be that which corresponds to a code of binary digits or “bits” (a term originally coined by John Turkey, as Shannon himself acknowledges). Indeed, this coding has been adopted as the informational unit par excellence ever since. His proposal is fundamentally based on the H measure of information known as “entropy”, which measures the degree of improbability (also usually interpreted in epistemic terms as “degree of uncertainty” or “unpredictability”) of each of the symbols that make up a message:

$${\rm{H}}({\rm{S}}) = - \sum {\rm{p}}({{\rm{s}}_{\rm{i}}})\log \,{\rm{p}}({{\rm{s}}_{\rm{i}}})$$

For example, the message “XVXWY” will have a higher entropy than the message “HELLO” if we consider the frequency of the English letters as the source. Therefore, Shannon defines his entropy concept of information as a measure of the “improbability” or “uncertainty” generated in the selection of a particular message or sequence of symbols by the information source, so that the enormous improbability of the occurrence of a sequence of signs such as “XVXWY” would translate into a large amount of information generated. Thus, this measure of information cannot be defined based only on a particular message, but on a message with respect to the distribution of probability, defined over the source or space of possible messages constructible by a certain alphabet of symbols. Another of the main characteristics of Shannon entropy is its disregard for the semantic content of the message i.e., the irrelevance of the reference of “HELLO”, in evaluating how improbable it is in a particular communicative scenario: “Frequently, the messages have meaning; that is they refer to or are correlated according to some systems with certain physical or conceptual entities. These semantic aspects of communication are irrelevant to the engineering problem” (Shannon [1948] 1993, 3. Italics in original). Therefore, Shannon’s communication theory would be postulated as a measure of the amount of information from sources, and in no case as a concept relating to the semantic information content of a particular message.

Another important aspect of this measure of entropy “H” is its formal similarity (based on the use of probability distributions and the use of the logarithmic function for its pragmatic virtues) with Boltzmann and Gibbs’ measure of statistical mechanical entropy: “the form of H will be recognized as that of entropy as defined in certain formulations of statistical mechanics” (ibid., 12). These formulations measure (roughly) the probability that the exact microscopic state of the physical system is in a cell or region of the space of possible molecular values or phase space. This mathematical similarity might lead to the choice of the term “entropy”—originally belonging to the field of statistical physics—to designate a measure of quantity of information. Tribus and McIving (1971) reported (from an interview with Shannon) that it was John von Neumann who suggested that he use that term, in order to exploit its profound misunderstanding within the scientific community. ⁴

As Shannon himself recognized, his proposal is presented as a highly sophisticated development that starts from Hartley’s (1928) analysis (where the latter’s measure of “information” is mathematically identical to Shannon’s entropy in the case of a uniform probability distribution over the symbols), which was not well known beyond the walls of the Bell Laboratories ⁵ . Unlike these pioneers, Shannon developed, throughout the 1940s (culminating in his 1948 paper), an extensive technical proposal on how to statistically evaluate and subsequently optimize the transmission of discrete and continuous messages in both noiseless and noisy channels, modeling this communicative process as a Markov chain. In short, we must emphasize once again that Shannon information is intrinsically independent of the meaning and physical character of the informational elements: “Shannon’s theory is a quantitative theory whose elements have no semantic dimension…. Moreover, Shannon’s theory is not tied to a particular physical theory but is independent of its physical interpretation” (Lombardi et al. 2016, 2000).

The director of the Division of Natural Sciences at the Rockefeller Foundation, Warren Weaver, immediately appreciated the possibilities of Shannon’s theory not only within the field of communication but also in other scientific domains. His role in the enormous immediate impact that the theory had within the scientific community was decisive, being that of popularizing Shannon’s technical proposal for the general public through an introductory commentary in the reprint of the original article in the famous book by Shannon and Weaver (1949). ⁶ Moreover, one of his main objectives (more or less implicit) was to elevate Shannon’s intellectual work to the Olympus of American science alongside authors like the physicist Gibbs and to generate a historical narrative (supported by certain comments of von Neumann, see our footnote 4) in which Shannon’s theory was the culmination of the statistical mechanics that started from Boltzmann: “Dr. Shannon’s work roots back, as von Neumann has pointed out, to Boltzmann’s observation, in some of his work on statistical physics (1984) that entropy is related to “missing information”, inasmuch as it is related to the number of alternatives which remain possible to a physical system after all the macroscopically observable information concerning it has been recorded” (Shannon & Weaver 1949, Note 1).

But Shannon’s communication theory was not the only information theory that became enormously popular in the scientific community of the United States in the late 1940s. Remarkably, mathematician Norbert Wiener independently developed the other great information theoretical proposal of the time, which he called “cybernetics” (Wiener 1948), and presented in a book of the same name, published in the same year as Shannon’s paper and based closely on the notion of self-regulating systems and feed-back communication. Interestingly, his statistical concept of information interpreted as “negative entropy of the observed system” was formally identical to that developed by Shannon, except for the difference in its sign. Although Weaver defended the contribution of cybernetics to Shannon’s theory “Dr. Shannon has himself emphasized that communication theory owes a great debt to Professor Norbert Wiener for much of its basic philosophy”. (Shannon & Weaver 1949, Footnote 1), the truth is that there are notable differences in substance between the two. Illustratively, while Shannon’s communication theory is a profoundly domain-specific treatise and far from any speculation beyond its technical content, Wiener’s cybernetics tended towards philosophical speculation and sought to become a broadly interdisciplinary theory: “In Wiener’s view, information was not just a string of bits to be transmitted or a succession of signals with or without meaning, but a measure of the degree of organization in a system” (Conway & Siegelman 2005, 132).

4. English vs. American information theory: The London Symposia in the 1950s

Having delimited the basic elements of both the English and the American school of what we currently known as “information theory”, in this section we will explore the main fundamental differences between the two since their initial socio-historical encounter in the early 1950s. ⁷ This meeting of the two information theories during this decade took place mainly in the context of the London Symposium of Information Theory, which was a series of conferences dedicated to the popularization (and also confrontation) of the advances in this field of research at an international and interdisciplinary level. ⁸

Shannon’s so-called communication theory (and in parallel also Wiener’s cybernetics) reached great heights of popularity in a very short time after its re-publication in the book co-authored with Weaver (Shannon & Weaver 1949). As Kline (2015, 110) points out, it was precisely in his early contact with the English information theoretical field at the first London Symposium on Information Theory in 1950 that Shannon’s theory became popularly known as “information theory” in the United States. However, in the intellectual context of the United Kingdom, certain authors such as Gabor, MacKay or Cherry were already using the expression “information theory” to refer to a disciplinary field substantially different from the statistical analysis of the communicative transmission of signals, namely: scientific methodology and practice (specifically measurement). As the empiricist-logical philosopher Yehoshua Bar-Hillel pointed out, “the British usage of this term [theory of information] moved away from Communication and brought it into close contact with general scientific methodology” (Bar-Hillel 1955, 97, 104). It was Bar-Hillel who grouped the theoretical work of Gabor, MacKay and Cherry under the umbrella term “European School of Information Theory” (ibid., 105), later redefined by McCulloch as the “English School”.

Information theory was not at all something that the American and English schools had in common during the 1950s, and its own object changed significantly depending on whether one was in the intellectual environment of the Bell Labs or that of Kings College. For the English school, the information-theoretical research program à la Gabor (1946) or MacKay (1969) was intended to be a general and interdisciplinary proposal about how physicists obtained information about their respective phenomena through their scientific descriptions. The American program, on the other hand, was restricted to the specific field of the statistical study of signal transmission. This comment by Gabor is a clear example of this:

The concept of Information has wider technical applications than in the field of communication engineering. Science in general is a system of collecting and connecting information about nature, a part of which is not even statistically predictable. Communication theory, thought largely independent in origin, thus fits logically into a larger physico-philosophical framework, which has been given the title of “Information Theory.” (Gabor 1953, 2-4; also Kline, 2015, 59-60)

As Gabor pointed out, information theory in the English sense defended by MacKay (1969) intended to encompass the celebrated communication theory of Shannon, although certain members of the American school resisted this assumption. This was the case of the American information scientist Robert Fano, who explicitly contradicted MacKay a letter to Colin Chery in early 1953, noting that the expression “information theory” encompassed four fields that were impossible to integrate into a single field of rigorous scientific study: (i) Shannon’s communication theory (1948); (ii) Gabor’s wave form analysis (1946); (iii) Fisher’s classical statistics (1934); and (iv) “miscellaneous speculations” that cannot be determined precisely and in a mathematically rigorous way (see Kline 2015, 112).

Of course, in this last point of Fano’s distinction lies an implicit critique from an American information-theoretical program (which adopted Shannon’s technically precise and not at all speculative theory as a paradigm) to the intellectually ambitious proposal of the young MacKay. However, as the 1950s passed, Shannon’s particular way of conceiving information theory began to gain followers among those who belonged to the intellectual sphere of influence of the English school, or even of Wiener’s cybernetics (1948). In this direction, Gabor (pioneer of the English school) manifested on several occasions a certain fear towards the theoretical foundations and philosophical claims of MacKay’s (1969) unified information theory, precisely because the latter’s use of his vaguely defined concept of information was significantly close to its ordinary semantic-epistemic sense as a synonym of “knowledge provider”. In this way, MacKay intended to convert his information theory into a sort of “naturalized” (or scientifically based) epistemology of scientific practices, analyzing how scientists acquired information about observed physical phenomena through practices such as measurement. This pseudo-philosophical aspiration repelled the most faithful followers of Shannon’s strictly technical paradigm, such as Fano or Peter Elias of MIT, due to Shannon’s own warnings against confusing his concept with the ordinary sense of it, which is closely connected with the semantic notion of “meaning”.

Undoubtedly, one of the fundamental differences between the American school of Shannon ([1948] 1993) and the English school of MacKay (1969) is that, while the former develops a concept of information independent of the semantic content of the messages “these semantic aspects of communication are irrelevant to the engineering problem” (Shannon [1948] 1993, 3), the latter is directly opposed to defending a concept of semantic information where “the theory of information has a natural, precise and objectively definable place for the concept of meaning” (MacKay 1969, 93). On the one hand, the concept of meaning included by MacKay in his informational proposal was but the consequence of appealing to the intentional capacity of the agents to refer (by means of a parameter O à la Fisher [1934] or an element of the phase space à la Gabor [1946]) to physical properties of the observed systems. On the other hand, the reception of a technical concept of information disconnected from its intuitive semantic sense was difficult to assimilate for the general public or for scientists dedicated to other disciplinary fields, as the anthropologist Margared Meid reproached Shannon at the eighth Macy Conference on Cybernetics in 1951 (Gleick 2010). In fact, the general tendency in the early 1950s (although we could also find similar tendencies today) was to implicitly reinterpret Shannon’s concept of information as a measure somehow sensitive to certain semantic properties of the objects considered. As the philosophers Carnap and Bar-Hillel pointed out:

Prevailing theory of communication (or transmission of information) deliberately neglects the semantic aspects of communication. … It has, however, often been noticed that this [semantic] asceticism is not always adhered to in practice and that sometimes semantically important conclusions are drawn from officially semantics-free assumptions. In addition, it seems that at least some of the proponents of communication theory have tried to establish (or to reestablish) the semantic connections which have been deliberately dissevered by others. (Carnap & Bar-Hillel 1952, 1)

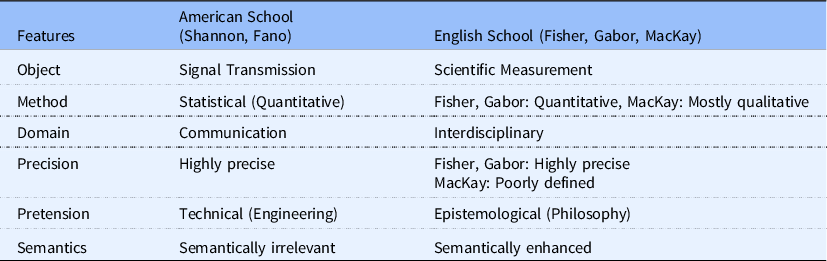
We would emphasize at this point that it was Carnap and Bar-Hillel who developed the first explicitly semantic quantitative and statistical theory of information in their “An Outline of a Semantic Information Theory” (Carnap & Bar-Hillel, 1952; see also Bar-Hillel & Carnap, 1952), developing a systematic-robust (though debatable) theoretical connection between a technical concept of information and a well-defined concept of meaning. Unlike MacKay’s (1969) proposal of descriptive metric or structural information, where its semantic character lies indefinitely in the intentionality of scientists to refer to phenomena by means of these informational tools, the well-defined technical measurement of “informational content” by Carnap and Bar-Hillel (1952) acquires semantic sensitivity by the capacity of the content of a particular proposition (e.g. resulting from a measurement) to eliminate possible alternative events. Beyond this proposition, not until the work of Fred Dretske (1981) would we see the first systematic theory of semantic information built on technical-theoretical resources coming directly from Shannon’s non-semantic information theory ([1948] 1993). Let us gather at this point the main differences (see table 1 below) that we have been outlining during this section between the American and English schools of information theories in the early 1950s, represented paradigmatically in the intellectual work of Shannon ([1948] 1993) and MacKay (1969), respectively.

Table 1. Comparative analysis of the American vs. English school of information theory

5. Understanding scientific measurement from a Shannonian perspective

In the previous section, we defined the clear differences that existed between the two schools in the early 1950s. However, the boundaries between them would progressively blur as the popularity and the various applications of Shannon’s theory grew within the scientific community. Shannon himself referred to this growing popularity as a “bandwagon” 1956, in reference to the exploitation of his mathematical theory of signal transmission by a vast plurality of disparate scientific fields such as molecular biology, statistical thermal physics or even social sciences: “Information theory has, in the last few years, become something of a scientific bandwagon…. Our fellow scientists in many different fields, attracted by the fanfare and by the new avenues opened to scientific analysis are using these ideas in their own problems” (Shannon [1956] 1993, 3).

Contrary to what it might seem, this uncontrolled climbing on Shannon’s “bandwagon” not represent an advance of what we have previously called the “American school”, at least in terms of the propagation of the fundamental elements of this information-theoretical school: its highly technical character and restricted domain, its statistical nature, or its lack of sensitivity to semantic content. Quite the contrary. Part of the scientific community began to take advantage of the disproportionate success of Shannon’s theory to theoretically confront prima facie problems completely removed from the communicative transmission of signals, as was the paradigmatic case (on which we will focus from now on) of understanding how scientific agents acquire knowledge about its target phenomena through measurement practices. That is, with the success of Shannon’s proposal, certain authors attempted to carry out the intellectual objectives of the English school (e.g. scientific measurement) under a certain Shannonian flavor, but with their own conceptual resources. Up to this point, we can formulate our main idea in this paper, namely that the central intellectual claim of the English school (i.e. to understand the epistemic dynamics underlying scientific measurement processes through informational concepts) went from being articulated through non-Shannonian informational notions in the late forties to being conceptually derived from Shannon’s theory in the mid-fifties, taking advantage of its overflowing popularity.

The central intellectual claim of the English school (i.e. to understand the epistemic dynamics underlying scientific measurement processes through informational concepts) went from being articulated through non-Shannonian informational notions in the late forties to being conceptually derived from Shannon’s theory in the mid-fifties, taking advantage of its overflowing popularity.

One of the most illustrative examples of this tendency is found in the article “Information, Measurement, and Quantum Mechanics” published by the American physicist Jerome Rothstein in 1951. In it, he proposes to understand the phenomenon of scientific measurement as a process of communication between the observer (or meter) and the observed physical system. To this end, Rothstein develops a detailed analogy between the different elements of a scientific measurement procedure and the elements of a communication process, as shown by the enormous similarity between the diagram used by Rothstein (see Figure 3, below) and the famous diagram used by Shannon in his 1948 founding article, see Figure 3. In his analogical argument, (i) the system of interest (e.g. one gram of Helium) represents the information source, from which is taken a property of interest (e.g. temperature), (ii) a measuring device (e.g. thermometer) represents the communicating transmitter which encodes said physical property in signals (e.g. 189º degrees Kelvin) to be transmitted by the media-communicative channel, and (iii) an indicator (e.g. scale on the thermometer), which decodes said measured value to be obtained by the destination (e.g. the observer agent carrying out the measurement).

Figure 3. Rothstein’s (1951) communication model of scientific measurement.

Therefore, in this proposal, Rothstein (1951) inherited the core theoretical aim of the English information-theory school (i.e., to provide an informational understanding of scientific measurement) by capitalizing certain conceptual tools of the American school, mainly its signal transmission communication model, see Figure 3 However, in carrying out this task, this physicist implicitly renounced the defining parameters of Shannon’s proposal (as noted above in Table 1). First, Rothstein develops a mainly qualitative account (against Shannon’s quantitative measure) of the information that an agent acquires about a physical system through measurement. By measuring the temperature of one gram of Helium, the observing agent acquires information that its temperature value is 189º. However, the fact that the measurement analogically constitutes a communicative process does not fix at all the amount of thermometric information that the observer acquires on that substance, while the Shannon entropy applicable to the information source is not sensitive to the number of thermometric values that would be thermophysically significant in a particular case. Furthermore, being strict with the communication theory when measuring the temperature of a gas, we would not obtain information about the current temperature value of that system (e.g. 189º) but about all possible temperature values that could be measured thermometrically, which is completely irrelevant for any observer in a scientific practice.

Secondly, the Rothstein analogy also implicitly rejects the fundamental dogma (on which the American school is based) that Shannon information is not semantic. By positing measurement procedures as communication processes, the information that the observer obtains at the end of the process has a semantic character that is inseparable from the model in which it is inserted. As we can see, the temperature value “189º K” as a sequence of signs that the observer receives after the measurement-communication (see figure 3) refers by default to a property of the observed system (i.e., it has the characteristic aboutness of all types of semantic information, see Dretske [1981, Section 2]), thus acquiring meaning. According to Rothstein’s proposal (1951), the amount of “thermometric” information that the observer would receive does not depend on the frequency of the signs that make up messages such as “189ºK” (assuming that the signs “1”, “8”, “9”, “º”, “K” belong to the alphabet of the information source) as proposed by Shannon’s theory but would essentially depend on their content. Note that this analogical approach makes no sense, since being precise and obtaining a highly infrequent thermometric value-message like “928ºK” would transmit to the observer much more Shannon information-entropy about one gram of Helium than a highly frequent thermometric value like “189ºK”.

Although Rothstein was part of that generation of North American scientists of the early fifties enormously influenced by the American school (in his 1951 paper he cites Hartley [1928] and Shannon [[1948] 1993] as references), and without apparent causal influence with the English school, his theoretical proposal could be classified (at least in a conceptual and not historiographical sense) within the latter precisely because of his intellectual pretension to give an informational account of the processes of scientific measurement and not to statistically analyze the optimal way of encoding messages. In Brillouin’s (1951) proposal, the subordination of tools and concepts proper to Shannon’s theory (as opposed to other informational notions available) to the objective of illuminating the processes of scientific measurement is a clear example of the intellectual process that we intend to evaluate here.

6. Confluence of the English-American School: Leon Brillouin

We have just presented Rothstein’s analogy in 1951 as a particular example of the intellectual trend that ended up imposing itself in his time, where the intellectual aims of the English school came to be assimilated within the bandwagon of Shannon’s theory. However, one of the paradigmatic cases of this tendency can be found in the intellectual work developed by the French-American physicist Léon Brillouin ⁹ (1889-1969) during the first half of the 1950s. Born in Sèvres, Brillouin belonged to a long line of French physicists, including his father, the pioneer of statistical mechanics in France Marcel Brillouin ¹⁰ , and his grandfather, Éleuthère Mascart. Trained under the supervision of Paul Langevin in quantum solid theory, Brillouin developed part of his career in French scientific institutions such as the Collège de France or the Institut Henri Poincaré. However, due to the war, he began to work in the United States (from the University of Wisconsin-Madison in 1942 to Harvard University during 1947-1949), where he developed a significant part of his scientific career, even becoming an American citizen in 1949. In the 1950s, Brillouin began working for IBM and Columbia. Brillouin would go down in history for his advances in solid state physics, in wave physics (in parallel with the information theorist Gabor) and of course for the systematic introduction of informational considerations into statistical thermal physics.

In spite of the relevance of his prolific scientific work and the great impact of his theoretical proposal (as we will try to demonstrate during this section), the intellectual work of Léon Brillouin in the ‘informationalization’ of the thermal physics of the fifties has been unjustly disregarded within the literature, except for particular cases, namely Leff and Rex (1990) or Earman and Norton (1999, 8). Undoubtedly, the chapter entitled “Leon Brillouin et la theorie de l’information” that Segal (2003) devotes to this author constitutes one of the most exhaustive analyses of Brillouin’s intellectual evolution to be found in the literature. Although he is usually cited for his proposal of a solution to Maxwell’s problem, the truth is that the theoretical and conceptual foundations underlying this proposal have not been properly evaluated either from either a historiographic or a philosophy of physics perspective: this will be precisely our task, showing Brillouin as the maximum exponent of the intellectual drift of what we have called “the English (or European) information-theory school” within the bandwagon of Shannon’s theory in the 1950s. Although his intellectual evolution in this particular field can be traced through several publications from the beginning of this decade (for example, his popular 1951 “Maxwell’s Demon Cannot Operate: Information and Entropy”.), to defend this thesis we will focus on the argument deployed in his famous book Science and Information Theory (Brillouin 1956), in which he concludes his development of an information theory applicable to the field of thermal physics.

In the Preface to the first edition of this book, Brillouin notes the rapid popularization of recent information theory, stating that “a new scientific theory has been born during the last few years, the theory of Information. It immediately attracted a great deal of interest and has expanded very rapidly” (Brillouin 1956, vii). But in what sense is the expression “information theory” used here?, In the broad way in which MacKay referred to a reflection on the obtaining of knowledge through scientific practices (English school)? Or in the specific way in which Fano referred to the statistical study of signal transmission? Without going any further, Brillouin seems to claim the latter meaning, linked to the theory proposed by Shannon ([1948] 1993). He notes that “this new theory was initially the result of a very practical and utilitarian discussion of certain basic problems: How is it possible to define the quantity of information contained in a message or telegram to be transmitted” (ibid). However, immediately afterwards, he claims to use his theoretical and technical resources in a particular way to carry out the central aim of the English information-theory school, noting that: “Once stated in a precise way, it can be used for many fundamental scientific discussions” (Ibid). This tension between: (i) claiming the Shannonian pedigree of his proposal, and (ii) developing a general theory of scientific information in the English way, will continue to permeate the entirety of this book.

At first sight, we could divide Science and Information Theory (Brillouin 1956) into two significantly different parts, tied together by a bridging chapter. In the first part of the book, from Chapter 1 “The Definition of Information” to Chapter 7 “Applications to Some Special Problems”, we find a detailed exposition of Shannon’s statistical theory and the communicative transmission of signs, without entering into physical considerations alien to the theory itself. In Chapter 8, entitled “The Analysis of Signals: Fourier Method and Sampling Procedures”, Brillouin addresses the physical character of continuous communicative signals, focusing on the information theory developed by Gabor (1946) based on the concept of “information cells” in the phase space of the waves that transmit the signals. The second part of the book (from Chapter 9 onwards) is devoted to a detailed exposition of his informational approach to the field of statistical thermal physics.

Interestingly, Brillouin states as early as Chapter 1 that the concept of information that he will use throughout the book will be the Shannon measure of entropy, emphasizing from the first moment its difference from the ordinary sense of the term “information” as synonymous with knowledge: “we define “information” as distinct from “knowledge”, for which we have no numerical measure…. Our definition of information is, nevertheless, extremely useful and very practical. It corresponds exactly to the problem of a communications engineer who must be able to transmit all the information contained in a given telegram” (Brillouin 1956, 9-10). With this defense of the technical concept of information, Brillouin seemed to be buying a first-class ticket on the 1950s Shannon bandwagon. But contrary to what the French-American physicist promised in this first chapter, in the second part of Science and Information Theory (in particular from Chapter 12 “The Negentropy Principle of Information”) he would start to implicitly employ a notion of information substantially different from Shannon’s (see Section 3), which would start to be predominant in all of concept of entropy (specifically in his famous Boltzmann formulation, i.e. S = k _B log W) as a measure of information: “A more precise statement is that entropy measures the lack of information about the actual structure of the system. This lack of information introduces the possibility of a great variety of microscopically distinct structures, which we are, in practice, unable to distinguish from one another” (Brillouin 1956, 160).

Before continuing with the analysis of Brillouin’s proposal, we must introduce some theoretically important clarifications. First, the Boltzmann entropy of a physical system is defined by the logarithm of the number of microscopic configurations W, compatible with a set of observable macroscopic values (temperature, pressure, volume, etc.) of the system at a given time, multiplied by Boltzmann’s constant k. Second, each microscopic (or technically “micro-state”) configuration of the system is determined by the position and speed of all the molecules that compose it, which are macroscopically indistinguishable and comparable to a set of configurations (or technically “macro-state”) compatible with the observational capacity of the agent-observer (Frigg 2008). Therefore, the statistical mechanical entropy of a system at a particular time will be proportional to the number of micro-states (or equivalently to the “volume of the phase space”) indistinguishable to the observer: the easier it is to distinguish the current micro-state, the lower the entropy of the system. Hence, Brillouin states that entropy measures the lack of “information” that an agent possesses with respect to the current microscopic configuration of the system, concluding that the information in this sense would be technically defined as differences or negative values of entropy -dS, which he called “negentropy”.

However, we have good reason to argue that this negentropic concept of information used by Brillouin does not correspond, for various reasons, to that technically defined by Shannon, but to its ordinary meaning (Brillouin 1956, 160), as a semantically-sensitive synonym of “knowledge” and relative to an agent (Floridi 2011). First, for this information to properly reflect Shannon’s entropic measure, it should be selected from an information source by means of an encoding process, analogous to how a message is selected from the source. Unlike Rothstein (1951), Brillouin does not establish a precise analogy between communication and measurement to specify these components, since entropy values (on which their negentropic information is defined) are not extracted directly by measurement, unlike, for example, temperature. Secondly, the Brillouinian concept of information is, unlike the Shannonian, explicitly semantic. This is clearly reflected in the “aboutness” (or referentiality, or what Dretske [1981] called “information that”) of the information or lack of information that an agent possesses “about” a microscopic configuration of the observed system, where a Brillouinian-negentropic information value refers directly to the microstates of the system about which the observer has information.

Thirdly, this negentropic information that we find in Science and Information Theory appeals in an evident way to the ordinary sense of the term “information” precisely because it refers in some way to the observational and macroscopic knowledge that a scientific agent-observer possesses about the inaccessible microscopic configuration of a molecular system. As Earman and Norton (1999) pointed out in their analysis of the Brillouinian information-theoretical proposal: “Brillouin’s labeling of the quantity as ‘information’ is intended, of course, to suggest our everyday notion of information as knowledge of a system” (Earman & Norton 1999, 8). It is here where it is shown that the main objective of Brillouin’s concept of information is similar to that of the members of the English information-theory school, namely: to understand from a scientific framework (i.e., naturalized) how scientific agents obtain knowledge about objective phenomena through various procedures such as observation, measurement or experimentation. This point is clearly seen in the statement that “any experiment by which information is obtained about a physical system produces, on the average, an increase of entropy in the system or in its surroundings” (Brillouin 1956, 184). Note that the term “information” that Brillouin employs in this quotation is (contrary to what he stated at the beginning, i.e. “information” as distinct from “knowledge” [Ibid., 9]) completely interchangeable with the basic epistemic concept of “knowledge” or similar, without changing at all its meaning, namely: “any experiment by which knowledge is obtained about a physical system”. In fact, the intrinsically epistemic character of his negentropic information serves Brillouin to carry out the main achievement by which he will go down in history: to solve Maxwell’s demon problem by stating that the acquisition of knowledge would necessarily entail an entropy increase in the system.

Briefly, Maxwell’s demon problem states in general terms that an agent that could manipulate the microscopic properties of systems could decrease their entropy, and thus violate the Second Law of Thermodynamics (Leff & Rex 1990). In his famous paper, Leo Szilard (1929) proposed a solution to Maxwell’s demon problem by stating that the acquisition of knowledge by the agent of the molecular components of the system implied an increase in the entropy of the system which would compensate for a plausible decrease in entropy, thus saving the Second Law of Thermodynamics. Brillouin (1951) sought to reformulate Szilard’s argument in theoretical and informational terms by substituting the term “knowledge” for the then-fashionable concept of “information”: “In other words [epistemic] information must always be paid for in negentropy, the price paid being larger than (or equal to) the amount of information received. An observation [acquisition of information] is always accompanied by an increase in entropy, and this involves an [entropy-generating] irreversible process” (Brillouin 1956, 184).

In this direction, scientific procedures such as observation or measurement are assimilated from Brillouin’s theoretical proposal as processes of information acquisition (semantic, epistemic) in the English sense (Gabor, 1946; MacKay, 1950) or as communicative processes à la Rothstein (1951). In fact, if we were to strictly employ the concept of Shannon entropy based on the possible microstates of the system, when a measurement is made on the system the information encoded in the microstatistical data would not increase (as predicted by Brillouin) but would decrease, precisely because the number of microstates compatible with the knowledge acquired after the measurement decreases. Thus, Brillouin’s choice of the particular information concept implicitly employed in his theoretical proposal is not a mere linguistic decision, but has epistemic consequences (i.e., when explaining or predicting) diametrically opposed to those we could obtain from the Shannon information concept he promised to use during his proposal. As we have shown, although Brillouin immediately climbs onto Shannon’s bandwagon as early as Chapter 1, he ends up at the end of the day developing a theory of scientific information that has nothing to do with it either theoretically (since Shannon’s [1948] 1993, communication model plays no role) or conceptually (since in Chapter 8 he already stops employing the notion from communication theory).

From the analysis we have made so far, we may conclude that however much Brillouin may claim that he has adopted Shannon’s communication theory, in the end he implicitly uses the ordinary sense of this term to give a new, fashionable and highly suggestive name to the already existing quantity of Boltzmann entropy. But as Earman and Norton pointed out, this new name adds nothing significantly new to the description of thermodynamic processes: “All that matters for the explanation is that the quantity I is an oddly labelled quantity of entropy and such quantities of entropy are governed by the Second Law of thermodynamics. The anthropomorphic connotations of human knowledge play no further role” (Earman & Norton 1999, 8). Going a step further than these two authors, one might also argue that this conceptual and terminological decision can illuminate how scientific agents obtain knowledge about their objective phenomena through common practices such as measurement or observation. Even if we can epistemically interpret the mechanical statistical concept as “lack of information”, this does not help us to understand in a robust way how the physically significant values of this measurement change depending on the behavior of the systems analyzed (Frigg 2008).

We would claim at this point that it is precisely in the Brillouinian concept of negentropic information where this author manifests himself (although he himself does not claim to do so) as one of the greatest exponents of the English school during the Shannonian hegemony in science in the 1950s. As we have just indicated, the value of the Brillouinian information that an agent possesses on a system is directly proportional to the volume of the space of phase W (or number of micro-states) of the macro state that represents the observational knowledge of this agent. This proposal is extremely close to the concept of “information” defined by Gabor (1946), who argued that the information transmitted by a wave signal is proportional to the number of elemental cells (sets in which the microstates of a system can be grouped) into which the volume of the phase associated with said wave signal can be divided. Gabor’s proposal was cited by Brillouin in section 8.8 of his book, entitled “Gabor’s Information Cells” (Brillouin 1956, Section 8.8)

After Gabor, MacKay (1969) also associated the information that an agent possesses about a system with the number of physical events (in this case, “microstates”) that are distinguishable with respect to the observational capacity of this agent, applying it to the paradigmatic case of scientific measurement: “A measurement could be thought as a process in which elementary physical events, each of some prescribed minimal significance, are grouped into conceptually distinguishable categories so as to delineate a certain form … with a given degree of precision … The ‘informational efficiency’ of a given measurement could be estimated by the proportion of those elementary events” (MacKay 1969, 3). Note that both MacKay in this quotation and Brillouin (1956) explain the measurement procedure in statistical mechanics in the same informational terms (although the latter claims to be dependent on the Shannonian program and the former does not). Namely, both claim that all measurement reduces the domain of events compatible with the pre-technical knowledge of the agent. In this direction, Figure 1 could be equivalently used to illustrate both Gabor-MacKay’s (1969) and Brillouin’s (1956) informational descriptions of scientific measurement procedures, except for the fact that the latter author used phase-volume-descriptions instead of Gaborian vector-descriptions.

Why, then, did Brillouin not claim himself as part of the English tradition but of the American-Shannonian one, even though (as we have defended in detail) his proposal is evidently closer to the first than to the second? The most plausible answer to this question belongs to the sociology of scientific knowledge. While the English information-theoretical school not only failed to consolidate itself disciplinarily and institutionally, but also became progressively discredited by the radical speculative proposal of MacKay (1969) (Section 4), Shannon’s theory was quickly consolidated among the scientific community of the 1950s. In this sense, if a proposal such as that of Rothstein (1951) or Brillouin (1956) were shown to be an intellectual member of the English school, it would enjoy immediate acceptance or faster assimilation due to the historical momentum of Shannon’s bandwagon. Moreover, Shannon’s bandwagon would serve as an excellent disciplinary vehicle to transmit certain ideas alien to the communicative transmission of signals within the fervor for this theory.

Of course, this strategy did not go unnoticed by those members of the community most critical of the informationalist drift acquired by the science of this era. Colin Cherry himself, a member of and critic of the English school, recognized the intellectual work of Brillouin (1956) as a more or less concealed manifestation of the English information-theory school (Section 2), which was prone to the evaluation of science: “this wider [than Shannon’s communication theory] field, which has been studied in particular by MacKay, Gabor, and Brillouin, as an aspect of scientific method, is referred to, at least in Britain, as information theory” (Cherry 1957, Italics are originals). In short, regardless of the historiographic possibility of establishing the intellectual influence of the English school on Brillouin (or its inclusion for geographical reasons), the interests of his proposal, centered on scientific measurements and not on the transmission of signals, place it immediately in the intellectual line of MacKay or Gabor.

7. Conclusion

Our main objective in this paper has been to comparatively analyze the intellectual evolution of the English information-theory school (originated in the work of Fisher [1934] and Gabor [1946], and radicalized in MacKay’s [1969] unifying proposal) in relation to Shannon’s communication theory ([1948] 1993), from before its publication until the entangled confluence of both theoretical programs in the early 1950s. After carrying out a thorough analysis of the reasons why the objectives and concepts of the English and the American schools (characterized by their intellectual aims, scientific measurements and signal-transmissions, respectively) were transformed during the period from 1946 to 1956, we will conclude by arguing that the English school did not simply disappear under the Shannonian tsunami of the 1950s, as could be derived from recent historiographical analyses such as Kline’s (2015). On the contrary, as the case of the scientific work of Léon Brillouin (1956) in his Science and Information Theory shows, the intellectual aim of the English school (i.e., to informationally explain the epistemic dynamics of scientific measurements) was carried on since the mid-fifties by capitalizing on the conceptual tools of Shannon’s communication theory.