Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Avis, David
Gum, Teren
and
Toussaint, Godfried
1986.
Visibility between two edges of a simple polygon.
The Visual Computer,
Vol. 2,
Issue. 6,
p.
342.
Sack, Jörg-Rüdiger
and
Toussaint, Godfried T.
1987.
Separability of pairs of polygons through single translations.
Robotica,
Vol. 5,
Issue. 1,
p.
55.
Dehne, Frank
and
Sack, Jörg-Rüdiger
1987.
Graph-Theoretic Concepts in Computer Science.
Vol. 246,
Issue. ,
p.
237.
Dehne, Frank
and
Sack, Jörg-Rüdiger
1987.
Translation separability of sets of polygons.
The Visual Computer,
Vol. 3,
Issue. 4,
p.
227.
Woo, Tony C.
1987.
Automatic Disassembly.
Vol. 1,
Issue. ,
Toussaint, Godfried T.
1988.
Pattern Recognition and Artificial Intelligence - Towards an Integration.
Vol. 7,
Issue. ,
p.
103.
Natarajan, B. K.
1989.
An analysis of assembly.
The Visual Computer,
Vol. 5,
Issue. 5,
p.
316.
Toussaint, G.
1989.
On separating two simple polygons by a single translation.
Discrete & Computational Geometry,
Vol. 4,
Issue. 3,
p.
265.
Houle, Michael E.
and
Toussaint, Godfried T.
2016.
Quadrangles which cannot be separated with two hands.
Vol. 1738,
Issue. ,
p.
480021.
Houle, Michael E.
and
Toussaint, Godfried T.
2017.
On the separability of quadrilaterals in the plane by translations and rotations.
Beiträge zur Algebra und Geometrie / Contributions to Algebra and Geometry,
Vol. 58,
Issue. 2,
p.
267.
Toussaint, Godfried
2018.
Moving a Chair through a Door: A Tutorial on Local Spatial Reasoning in Algorithmic Robotics.
IOP Conference Series: Materials Science and Engineering,
Vol. 435,
Issue. ,
p.
012043.
Toussaint, Godfried T.
2018.
Motion Planning Problems with Boxes: An Introduction for Undergraduate Courses in Discrete Mathematics.
p.
73.
Toussaint, Godfried T.
2019.
Information Systems and Technologies to Support Learning.
Vol. 111,
Issue. ,
p.
580.


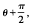 ,
,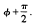 . Furthermore, a direction for carrying out such a translation can be determined in O(
. Furthermore, a direction for carrying out such a translation can be determined in O(