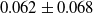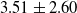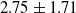1. Introduction
Continuum robots could easily change their configurations due to external contact, which will affect the robot motion and eventually alter the control efforts [Reference Chen, Wang, Galloway, Godage, Simaan and Barth1, Reference Xiao, Musa, Godage, Su and Chen2]. The contact force is of great significance especially in medical settings such as cardiac ablation surgery, where the ablation area of the tissue largely depends on the contact force [Reference Kesner and Howe3]. Many work has been done to estimate the contact forces. Contact force can be directly measured by embedding miniature force sensors on the robot body [Reference Mitsuishi, Sugita and Pitakwatchara4, Reference Valdastri, Harada, Menciassi, Beccai, Stefanini, Fujie and Dario5]. However, these methods are only effective when the contact occurs at the sensor location, for instance at the tip of the robot. Also, the strict dimension constraints also limit the wide application of these approaches in needle-sized continuum robots, especially in the minimally invasive surgical tools where the tool tip often equipped with multiple treatment or diagnosis units [Reference Alipour, Meyer, Dumoulin, Watkins, Elahi, Loew, Schweitzer, Olson and Chen6, Reference Gunderman, Schmidt, Viswanathan, Halperin, Tokuda, Seethamraju and Chen7]. Alternatively, continuum robot task-space contact force can be estimated based on joint-space sensor measurement. For example, Bajo et al. [Reference Bajo and Simaan8, Reference Bajo and Simaan9] proposed a method for tendon-driven continuum robot contact force sensing, but this requires a dedicated force cell at the actuation unit. The joint-space force cells may not be available for some continuum devices such as concentric tubes [Reference Chen, Poorman, Comber, Pitt, Liu, Godage, Yu, Grissom, Barth and Webster10], steerable needles [Reference Chen, Godage, Sengupta, Liu, Weaver and Barth11], or in MR-guided interventions [Reference Chen, Howard, Godage and Sengupta12–Reference Kwok, Lee, Chen, Wang, Hu, Chow, Zhang, Stevenson, Kwong, Luk and Schmidt15] where the MRI-conditional force sensor is not readily available.1
Alternatively, force can be estimated implicitly based on the measurements of continuum robot configuration change. This is applicable since the intrinsic compliant nature of continuum robots allows the robot configuration to be changed with the contact forces [Reference Webster and Jones16]. Many models have been proposed to predict the continuum robot shape based on contact force, including beam-based method [Reference Stilli, Kolokotronis, Fraś, Ataka, Althoefer and Wurdemann17], calibration method [Reference Wang and Simaan18], variable curvature method [Reference Mahl, Hildebrandt and Sawodny19], and Cosserat rod theory [Reference Rucker, Jones and Webster20]. Contact forces, in turn, can be estimated by matching the measured shape with model shape.
Related works have been published to estimate the contact force using shape-based method, which compares the difference between measured shape and model shape in the point cloud. Qiao [Reference Qiao, Borghesan, De Schutter and Poorten21] proposed a shape-based method to estimate contact forces by minimizing the difference between the measured shape and model shape with Kalman filters. However, the estimation error is relatively large, with force mean error of 30.59% and locations mean error of 17.20%. Aloi [Reference Aloi and Rucker22] proposed a shape-based method using Fourier transformation. This method will estimate the force in a distributed fashion and can detect the force location by observing the "peaks” of the distributed force profile. However, it cannot provide useful information on the exact force magnitude and location if it is point contact.
Aside from shape-based method, curvatures can provide more robust information for force estimation. This is because the curvatures remain invariant for any translations or rotations the continuum robot undergoes. The curvatures along the continuum robot can be measured using multicore fiber Bragg grating (FBG) sensors [Reference Gouveia, Jorge, Baptista and Frazao23, Reference Xu, Yurkewich and Patel24] or intraoperative images with curvature estimation algorithms [Reference Frette, Virnovsky and Silin25–Reference Pottmann, Wallner, Yang, Lai and Hu29]. Several curvature-based methods have been investigated for force estimation. Qiao [Reference Qiao, Willems, Borghesan, Ourak, De Schutter and Poorten30] utilized FBGS to measure the curvatures along the manipulator and calculated the force (mean error of 9.8% error) and locations (mean error of 3.6% error) directly using constitutive law. Al-Ahmad [Reference Al-Ahmad, Ourak, Vlekken and Poorten31] utilized an unscented Kalman filter to the measured curvatures, which achieved 7.3% error of force magnitude and 4.6% error of location. However, the estimated location error is still large because these methods cannot solve subnode accuracy and require expensive FBG sensors embedded in the instrument.
In this paper, we present a curvature-based force estimation method that enables force estimation in a subnode accuracy. We also illustrate curvature-based method has advantages over shape-based method regarding the loss map convexity. Moreover, a local frame representation of Cosserat rod theory is derived to achieve faster curvature computation, which avoids the time-consuming integration of rotation matrix. Aside from obtaining the curvature feedback from FBG sensors, we also investigate the feasibility of obtaining the curvature from image feedback using the line integral method. The result shows that the contact force locations and magnitudes can be accurately estimated by curvature from both FBG sensors and images. The contributions of this paper include:
-
• Distributed the contact force to adjacent nodes to solve the model in subnode accuracy.
-
• Derived a local frame representation of Cosserat rod theory to achieve faster computation.
-
• Investigated the method to compute local curvature based on image feedback.
-
• Experimentally validated the proposed estimation method on single and multiple contact force cases.
The structure of the paper is arranged as follows. Section 2 describes the derivation of a local frame representation of Cosserat rod theory for curvature calculation. Section 3 discusses the method to solve the model in subnode accuracy and the methods to compute the feedback curvatures from multicore FBG sensors and the images. Section 4 shows the experimental results of the force estimation regarding the force magnitudes and the locations. Finally, Section 5 is the conclusion.
2. Model curvature calculation
2.1. Review of Cosserat rod model
Cosserat rod model describes the equilibrium state of a small segment of thin rod subjected to internal and external distributed forces and moments. Previous works [Reference Jones, Gray and Turlapati32] have detailed the differential geometry of a thin rod with Cosserat rod theory so that the deformation can be estimated by solving Ordinary differential equations (ODEs) in (1)–(4) given external forces
![]() $\boldsymbol{F}_{e}$
and external moments
$\boldsymbol{F}_{e}$
and external moments
![]() $\boldsymbol{L}_e$
. To distinguish variables from different frames, we use lowercase letters for variables in local frame and uppercase letters for variables in global frame.
$\boldsymbol{L}_e$
. To distinguish variables from different frames, we use lowercase letters for variables in local frame and uppercase letters for variables in global frame.
where the dot symbol in
![]() $\dot{\boldsymbol{x}}$
represents the derivative of
$\dot{\boldsymbol{x}}$
represents the derivative of
![]() $\boldsymbol{x}$
respect to the arc length
$\boldsymbol{x}$
respect to the arc length
![]() $s$
, hat symbol in
$s$
, hat symbol in
![]() $\hat{\boldsymbol{x}}$
reconstruct vector
$\hat{\boldsymbol{x}}$
reconstruct vector
![]() $\boldsymbol{x}$
to a 3 by 3 skew symmetric matrix,
$\boldsymbol{x}$
to a 3 by 3 skew symmetric matrix,
![]() $\boldsymbol{P}$
is the shape in global frame,
$\boldsymbol{P}$
is the shape in global frame,
![]() $R$
is the rotation matrix of local frame relative to the global frame,
$R$
is the rotation matrix of local frame relative to the global frame,
![]() $\boldsymbol{N}$
and
$\boldsymbol{N}$
and
![]() $\boldsymbol{M}$
are internal force and moment in global frame which obeys the constitutive law
$\boldsymbol{M}$
are internal force and moment in global frame which obeys the constitutive law
![]() $\boldsymbol{v}$
and
$\boldsymbol{v}$
and
![]() $\boldsymbol{u}$
are differential geometry parameters of a rod,
$\boldsymbol{u}$
are differential geometry parameters of a rod,
![]() $\boldsymbol{v}^*$
and
$\boldsymbol{v}^*$
and
![]() $\boldsymbol{u}^*$
are differential geometry parameters of a rod with no external loads.
$\boldsymbol{u}^*$
are differential geometry parameters of a rod with no external loads.
![]() $K_{SE}$
and
$K_{SE}$
and
![]() $K_{BT}$
are the stiffness matrices. The boundary conditions for solving the ODEs (1)–(4) are described as
$K_{BT}$
are the stiffness matrices. The boundary conditions for solving the ODEs (1)–(4) are described as
where
![]() $\boldsymbol{F}_{tip}$
and
$\boldsymbol{F}_{tip}$
and
![]() $\boldsymbol{T}_{tip}$
are external force and torque applied at the tip.
$\boldsymbol{T}_{tip}$
are external force and torque applied at the tip.
![]() $loc_{tip}$
is the tip position in arc length. Thus, the rod shape
$loc_{tip}$
is the tip position in arc length. Thus, the rod shape
![]() $\boldsymbol{P}$
can be computed by solving the boundary value problem (BVP).
$\boldsymbol{P}$
can be computed by solving the boundary value problem (BVP).
2.2. ODEs for model curvature calculation
The widely accepted Cosserat rod model in (1)–(4) are expressed in global frame. But it is beneficial to use the model in local frame to calculate the curvatures. We firstly take the derivative of
![]() $\boldsymbol{M}$
in (6) and combine with (4)
$\boldsymbol{M}$
in (6) and combine with (4)
Then, using the relation
![]() $\dot{\boldsymbol{P}}\times \boldsymbol{N} = \hat{\dot{\boldsymbol{P}}}\boldsymbol{N}$
,
$\dot{\boldsymbol{P}}\times \boldsymbol{N} = \hat{\dot{\boldsymbol{P}}}\boldsymbol{N}$
,
![]() $\dot{\boldsymbol{P}} = R\boldsymbol{v}$
, and
$\dot{\boldsymbol{P}} = R\boldsymbol{v}$
, and
![]() $\hat{(R\boldsymbol{v})} = R\hat{\boldsymbol{v}}R^T$
(this is true when
$\hat{(R\boldsymbol{v})} = R\hat{\boldsymbol{v}}R^T$
(this is true when
![]() $R \in SO(3)$
), we can obtain
$R \in SO(3)$
), we can obtain
Multiplying
![]() $R^T$
on both side, and solve for
$R^T$
on both side, and solve for
![]() $\dot{\boldsymbol{u}}$
, we can have
$\dot{\boldsymbol{u}}$
, we can have
We define local variables
![]() $\boldsymbol{n} = R^T\boldsymbol{N}$
, and
$\boldsymbol{n} = R^T\boldsymbol{N}$
, and
![]() $l_e = R^T\boldsymbol{L}_e$
. The meaning of the variables
$l_e = R^T\boldsymbol{L}_e$
. The meaning of the variables
![]() $\boldsymbol{n}$
and
$\boldsymbol{n}$
and
![]() $\boldsymbol{l}_e$
are actually the variables
$\boldsymbol{l}_e$
are actually the variables
![]() $\boldsymbol{N}$
and
$\boldsymbol{N}$
and
![]() $\boldsymbol{L}_e$
expressed in local frame, respectively. Hence, (11) becomes
$\boldsymbol{L}_e$
expressed in local frame, respectively. Hence, (11) becomes
In order to solve
![]() $\boldsymbol{n}$
, we use (3) and multiply
$\boldsymbol{n}$
, we use (3) and multiply
![]() $R^T$
on the two sides and add
$R^T$
on the two sides and add
![]() $\dot{R}^T\boldsymbol{N}$
, which gives
$\dot{R}^T\boldsymbol{N}$
, which gives
Again, we define
![]() $R^T\boldsymbol{F}_e = \boldsymbol{f}_e$
. Notice that the left-hand side in (13) is actually the derivative of
$R^T\boldsymbol{F}_e = \boldsymbol{f}_e$
. Notice that the left-hand side in (13) is actually the derivative of
![]() $R^T\boldsymbol{N}$
, which is
$R^T\boldsymbol{N}$
, which is
![]() $\dot{\boldsymbol{n}}$
.
$\dot{\boldsymbol{n}}$
.
![]() $\dot{R}$
can be replaced by (2) on the right-hand side. Thus, we have
$\dot{R}$
can be replaced by (2) on the right-hand side. Thus, we have
To sum up, the curvatures of a general rod can be calculated by
with boundary conditions
where
![]() $loc_{tip}$
and
$loc_{tip}$
and
![]() $f_{tip}$
are the location and applied external force at the tip, respectively. (15) and (16) can be simplified in a special case where the rod is straight (
$f_{tip}$
are the location and applied external force at the tip, respectively. (15) and (16) can be simplified in a special case where the rod is straight (
![]() $\boldsymbol{u}^* = \textbf{0}$
and
$\boldsymbol{u}^* = \textbf{0}$
and
![]() $\boldsymbol{v}^* = [0\quad 0\quad 1 ]^T$
), with circular cross-section (
$\boldsymbol{v}^* = [0\quad 0\quad 1 ]^T$
), with circular cross-section (
![]() $K_{11} = K_{22} = K_{33}/2$
), nonshear and inextensible (
$K_{11} = K_{22} = K_{33}/2$
), nonshear and inextensible (
![]() $\boldsymbol{v} = [0\quad 0\quad 1 ]^T$
), and no external moment (
$\boldsymbol{v} = [0\quad 0\quad 1 ]^T$
), and no external moment (
![]() $\boldsymbol{l}_e=\textbf{0}$
). The simplified ODEs can be written as
$\boldsymbol{l}_e=\textbf{0}$
). The simplified ODEs can be written as
where
![]() $x$
,
$x$
,
![]() $y$
, and
$y$
, and
![]() $z$
are the first, second, and third component of a vector, respectively.
$z$
are the first, second, and third component of a vector, respectively.
![]() $K_{BT,ij}$
means the entry of
$K_{BT,ij}$
means the entry of
![]() $K_{BT}$
at row
$K_{BT}$
at row
![]() $i$
and column
$i$
and column
![]() $j$
. And (21)–(23) is the same as (16). Note that both the integral variables and the boundary conditions are defined in local frame, the curvature
$j$
. And (21)–(23) is the same as (16). Note that both the integral variables and the boundary conditions are defined in local frame, the curvature
![]() $u_x$
and
$u_x$
and
![]() $u_y$
can be solved by simple backward integration from the distal point (
$u_y$
can be solved by simple backward integration from the distal point (
![]() $s = L$
) to the proximal point (
$s = L$
) to the proximal point (
![]() $s = 0$
), which requires no iterative computation to solve a standard BVP. Therefore, the computational complexity is only determined by the number of nodes we divide along the arc length. Moreover, solving (19)–(23) will lead to the same result as solving the model in (1)–(4), but the former method will have faster performance for curvature calculation.
$s = 0$
), which requires no iterative computation to solve a standard BVP. Therefore, the computational complexity is only determined by the number of nodes we divide along the arc length. Moreover, solving (19)–(23) will lead to the same result as solving the model in (1)–(4), but the former method will have faster performance for curvature calculation.
3. Force estimation approach
3.1. Point forces for Cosserat model
The force defined in Cosserat rod theory is distributed force whose unit is N/m. However, the objective of this paper is to estimate the magnitude and location of point force whose unit is N. Conversion has to be performed between point force and distributed force. Firstly, we define the applied point forces in a new force vector which contains the locations and magnitude components of all forces.
where
![]() $s^i$
is the location of the
$s^i$
is the location of the
![]() $i^{th}$
point force,
$i^{th}$
point force,
![]() $f_{pt,x}^i$
and
$f_{pt,x}^i$
and
![]() $f_{pt,y}^i$
are the components of the
$f_{pt,y}^i$
are the components of the
![]() $i^{th}$
point force, and
$i^{th}$
point force, and
![]() $h$
is the total number of forces acting on the continuum robot. The arc length of the manipulator can be divided into
$h$
is the total number of forces acting on the continuum robot. The arc length of the manipulator can be divided into
![]() $q-1$
segments, and this gives
$q-1$
segments, and this gives
where
![]() $loc_i$
is the location of the
$loc_i$
is the location of the
![]() $i^{th}$
node,
$i^{th}$
node,
![]() $\boldsymbol{Loc}$
is the whole list of the nodes. In order to achieve subnode accuracy, we convert the point forces to distributed forces
$\boldsymbol{Loc}$
is the whole list of the nodes. In order to achieve subnode accuracy, we convert the point forces to distributed forces
![]() $\boldsymbol{f}_{vec}$
on the nodes
$\boldsymbol{f}_{vec}$
on the nodes
![]() $\boldsymbol{Loc}$
. Figure 1 shows an example to distribute the point force
$\boldsymbol{Loc}$
. Figure 1 shows an example to distribute the point force
![]() $f^i_{pt}$
to two adjacent nodes
$f^i_{pt}$
to two adjacent nodes
![]() $j-1$
and
$j-1$
and
![]() $j$
, the point force is distributed linearly according to the arc length distance between the two nodes. Therefore, the distributed forces can be calculated by
$j$
, the point force is distributed linearly according to the arc length distance between the two nodes. Therefore, the distributed forces can be calculated by
where
![]() $f^j$
(N/m) is the distributed force,
$f^j$
(N/m) is the distributed force,
![]() $f_{pt}^i$
(N) is the point force,
$f_{pt}^i$
(N) is the point force,
![]() $loc_{j-1}$
and
$loc_{j-1}$
and
![]() $loc_j$
are two adjacent nodes for
$loc_j$
are two adjacent nodes for
![]() $s^i$
. Note that the
$s^i$
. Note that the
![]() $s^i$
is located between hte nodes
$s^i$
is located between hte nodes
![]() $loc_{j-1}$
and
$loc_{j-1}$
and
![]() $loc_j$
, which allows the model to solve the solution in subnode accuracy. In the case where multiple point forces are close and distributed to the same node, the forces on that node will be superposed. After knowing the distributed forces along the rod, the mechanics model is complete and curvature can then be calculated through the integration of (19)–(23).
$loc_j$
, which allows the model to solve the solution in subnode accuracy. In the case where multiple point forces are close and distributed to the same node, the forces on that node will be superposed. After knowing the distributed forces along the rod, the mechanics model is complete and curvature can then be calculated through the integration of (19)–(23).

Figure 1. Distribution of point force to adjacent nodes to achieve subnode accuracy.

Figure 2. Loss maps computed by (a) shape (b) curvature.
3.2. Curvature-based force estimation
A robust method for force estimation is to minimize the least square loss between the calculated curvature with measured curvatures.
where
![]() $\boldsymbol{u}_{cal}$
is the curvature calculated from
$\boldsymbol{u}_{cal}$
is the curvature calculated from
![]() $\boldsymbol{f}_{vec}$
and
$\boldsymbol{f}_{vec}$
and
![]() $\tilde{\boldsymbol{u}}$
is the curvature measured by sensors.
$\tilde{\boldsymbol{u}}$
is the curvature measured by sensors.
Similar to minimizing the loss of curvature, the loss of shape
![]() $loss_{P}(\boldsymbol{f}_{vec})$
could also be used for the objective function of the optimization algorithm. Figure 2 shows a simulation example of the loss of shape
$loss_{P}(\boldsymbol{f}_{vec})$
could also be used for the objective function of the optimization algorithm. Figure 2 shows a simulation example of the loss of shape
![]() $loss_{P}(\boldsymbol{f}_{vec})$
and loss of curvature
$loss_{P}(\boldsymbol{f}_{vec})$
and loss of curvature
![]() $loss_{u}(\boldsymbol{f}_{vec})$
with various force magnitudes and locations. The loss map is calculated by following steps: 1) Choosing
$loss_{u}(\boldsymbol{f}_{vec})$
with various force magnitudes and locations. The loss map is calculated by following steps: 1) Choosing
![]() $\boldsymbol{f}_{vec} = [200\quad 0.3\quad 0 ]^T$
as the ground truth, and calculate the curvature
$\boldsymbol{f}_{vec} = [200\quad 0.3\quad 0 ]^T$
as the ground truth, and calculate the curvature
![]() $\tilde{\boldsymbol{u}}$
and shape
$\tilde{\boldsymbol{u}}$
and shape
![]() $\tilde{\boldsymbol{p}}$
using Cosserat rod theory. The
$\tilde{\boldsymbol{p}}$
using Cosserat rod theory. The
![]() $\tilde{\boldsymbol{u}}$
and
$\tilde{\boldsymbol{u}}$
and
![]() $\tilde{\boldsymbol{p}}$
can be assumed as the measured data from sensors. 2) Calculate
$\tilde{\boldsymbol{p}}$
can be assumed as the measured data from sensors. 2) Calculate
![]() $\boldsymbol{u}_{cal}$
and
$\boldsymbol{u}_{cal}$
and
![]() $\boldsymbol{P}_{cal}$
with the same method, but use different
$\boldsymbol{P}_{cal}$
with the same method, but use different
![]() $\boldsymbol{f}_{vec}$
whose first component ranges from 100 to 290 mm and the second component ranges from 0 to 0.5 N. 3) Use (28) to compute the loss for each pair of force magnitude and location. As illustrated in Fig. 2, the loss of curvature (b) shows better convex property than that of shape coordinates (a), and thus more robust results can be calculated [Reference Bubeck33]. Therefore, we use curvature-based method to estimate the force.
$\boldsymbol{f}_{vec}$
whose first component ranges from 100 to 290 mm and the second component ranges from 0 to 0.5 N. 3) Use (28) to compute the loss for each pair of force magnitude and location. As illustrated in Fig. 2, the loss of curvature (b) shows better convex property than that of shape coordinates (a), and thus more robust results can be calculated [Reference Bubeck33]. Therefore, we use curvature-based method to estimate the force.

Figure 3. Compute the curvatures using template disk.
![]() $A_I$
is the area surrounded by the template disk and the shape, and
$A_I$
is the area surrounded by the template disk and the shape, and
![]() $b$
is the radius of the template disk.
$b$
is the radius of the template disk.
3.3. Curvature feedback
Curvature feedback of a elastic tube can be obtained from either FBG sensors or images. For curvature measurement using FBG sensors, multicore FBG fiber is typically used to compute the curvature through the change of the Bragg wavelength [Reference Moore and Rogge34]. In this paper, the curvature measurement using FBG sensors is obtained directly from the software Shape Sensing v1.3.1 provided by the supplier.
To obtain the curvature feedback from the intraoperative image feedback, one of the major challenges is that the shape of the tube on the image is noisy, especially when the resolution of the image is low. This is because the tube shape can only be discretely captured by pixels of the image and the resulting centerline of the tube is not continuous. Thus, it is inapplicable to compute the curvature based on the basic geometry, which is the norm of the derivative of the tangent direction. The derivative of a noisy shape will increase the noise magnitude and reduce the quality of the curvature feedback. Many methods have been proposed to reduce the noise of the curvature feedback from the image feedback, including segmentation methods [Reference Nguyen and Debled-Rennesson27, Reference Nguyen and Debled-Rennesson28] and integral invariant methods [Reference Lin, Chiu, Widder, Hu and Boston26, Reference Pottmann, Wallner, Yang, Lai and Hu29]. In this paper, we implemented the integral invariant method proposed in ref. [Reference Frette, Virnovsky and Silin25] to compute the curvature feedback of the elastic tube from an image, which can be described as
where
![]() $\Vert \boldsymbol{u} \Vert$
is the norm of the curvature feedback at the center of the template disk,
$\Vert \boldsymbol{u} \Vert$
is the norm of the curvature feedback at the center of the template disk,
![]() $A_I$
is the area surrounded by the template disk and the shape, and
$A_I$
is the area surrounded by the template disk and the shape, and
![]() $b$
is the radius of the template disk (see Fig. 3). However, this integral invariant method can only be used to compute the curvature feedback of a tube if the tube only has in-plane bending. Special care has to be taken to compute the curvature feedback from image of a tube with out-of-plane bending, which will be the focus of our future work.
$b$
is the radius of the template disk (see Fig. 3). However, this integral invariant method can only be used to compute the curvature feedback of a tube if the tube only has in-plane bending. Special care has to be taken to compute the curvature feedback from image of a tube with out-of-plane bending, which will be the focus of our future work.
4. Experiments and results
In this section, we will validate the curvature-based force estimation method on single, double, and triple point force cases, with the curvature measured from FBG sensors or calculated via image feedback.
4.1. Force estimation result using multicore FBG sensors
4.1.1. Experiment setup
As illustrated in Fig. 4, the experiments were performed by adding multiple forces to a straight Nitinol tube. ATI force sensor (ATI Industrial Automation, United States) with 3D printed probe was mounted on a fixed vertical board. The probes are designed with different height in order to contact the Nitinol tube at various location and orientation (Fig. 4(c)). For every single probe that mounted on the force sensor, a counterpart probe (Fig. 4(a) and (b)) is also designed to keep the same distance from the probe head to the wall. This allows the force sensor with probe to be interchangeable with its counterpart such that the shape of Nitinol tube shape remains unchanged. For example, the Nitinol tube in Fig. 4(a) and (b) has the same shape, but the location of the force sensor is swapped. Thus, we can use one force sensor to measure multiple external forces. Fiber Bragg gratings sensors (FBGS International NV, Belgium) was inserted inside the Nitinol tube to measure the curvature.

Figure 4. Experiment setup for force estimation. The ATI force sensor with a probe is mounted on a fixed vertical wall. The FBGS is inserted inside Nitinol tube for curvature measurement. Counterpart of each force sensor with probe are designed to keep the shape of Nitinol in (a) and (b) the same, and the force sensor can swap the location. Different height design of the probe in (c) allows for 3D shape deformation.
4.1.2. System parameter calibration
The system calibration was conducted in two steps: (1) location calibration and (2) stiffness calibration. Since the FBGS fiber is transparent, it is hard to identify the locations of gratings inside the fiber. But the relative locations (spacing between adjacent gratings) are specified on the user manual (20 mm). The objective of location calibration is to ensure the curvatures we measured are aligned with the positions on the Nitinol. Three cases of single force at different locations were recorded, and the bias of the location can be minimized by adding an offset to the results.
where
![]() $s_{est}$
is the estimated location of the external force,
$s_{est}$
is the estimated location of the external force,
![]() $s_{cal}$
is the result of the model, and
$s_{cal}$
is the result of the model, and
![]() $s_{bias}$
is the bias to offset the error. After location calibration, we conducted stiffness calibration to match the calculated force magnitude with the measured force magnitude. Notice that the stiffness change has trivial impact on the location estimation, therefore the location calibration is still valid after completing the stiffness calibration. The result of the calibration is listed in Table I.
$s_{bias}$
is the bias to offset the error. After location calibration, we conducted stiffness calibration to match the calculated force magnitude with the measured force magnitude. Notice that the stiffness change has trivial impact on the location estimation, therefore the location calibration is still valid after completing the stiffness calibration. The result of the calibration is listed in Table I.
Table I. Calibrated parameters.

4.1.3. Force estimation results
The error analysis of the force estimation result is grouped into three categories: single force estimation analysis, double forces estimation analysis, and triple forces estimation analysis. For each category, the experiment was performed 13 times by applying varying contact force (0.27–1.96 N) at 13 different locations on the Nitinol tube. The step size of the integration of the ODEs for curvature calculation is
![]() $ds =$
1 mm.
$ds =$
1 mm.
As summarized in Table II, the RMSE of single force estimation, double force estimation, and triple force estimation are
![]() $0.037 \pm 0.069$
N,
$0.037 \pm 0.069$
N,
![]() $0.060 \pm 0.046$
N, and
$0.060 \pm 0.046$
N, and
![]() $0.127 \pm 0.081$
N, respectively. Therefore, the proposed method can estimate the force magnitude accurately, despite the fact that larger number of forces can slightly reduce the estimation accuracy on force magnitude. The RMSE of the single-location estimation, double-location estimation, and triple-location estimation is 2.95
$0.127 \pm 0.081$
N, respectively. Therefore, the proposed method can estimate the force magnitude accurately, despite the fact that larger number of forces can slightly reduce the estimation accuracy on force magnitude. The RMSE of the single-location estimation, double-location estimation, and triple-location estimation is 2.95
![]() $\pm$
2.17 mm,
$\pm$
2.17 mm,
![]() $2.58\pm 2.06$
mm, and
$2.58\pm 2.06$
mm, and
![]() $4.69\pm 4.06$
mm, respectively. This indicates that a larger location error will occur when the number of external forces increases.
$4.69\pm 4.06$
mm, respectively. This indicates that a larger location error will occur when the number of external forces increases.
Table II. Force estimation RMSE using FBG sensor feedback.


Figure 5. Experimental results for single force estimation. (a) Force magnitude estimation. (b) force location estimation.
Figures 5 and 6 summarize the force estimation results for single force and multiple forces, respectively. The blue dots are the predicted result and the red dots are the measured results. Most of the cases in Fig. 5 can be predicted accurately except case 1 (error magnitude of 8.72%). This error occurs because the curvature can only be measured by the first few gratings (the spacing of adjacent gratings is 20 mm), while the rest gratings will read 0 because no internal moment exists after the location where the force is applied. In Fig. 6, each case has two or three values, which refer to the two or three forces, respectively. The red dots and the blue dots are aligned well with each other, which demonstrates the accuracy of the proposed estimation method.

Figure 6. Experimental results for double and triple forces estimation. (a) Force magnitudes estimation. (b) force locations estimation. During each experiment, the circle marker indicates the first force, diamond marker indicates the second force, and the triangle marker indicates the third force (triple force scenario).
4.2. Force Eestimation result using image feedback
In this subsection, we investigate the potential application of curvature-based force estimation method in image-guided interventions. We assume the continuum robot with in-plane bending so that its shape can be captured by one image. However, the 3D shape reconstruction of the continuum robot with out-of-plane bending can be achieved by images captured from multiple viewing angles or 3D imaging techniques such as MRI [Reference Kwok, Chen, Chau, Luk, Nilsson, Schmidt and Zion35] or 3D ultrasould imaging [Reference Dai, Lei, Roper, Chen, Bradley, Curran, Liu and Yang36].
4.2.1. Workflow to estimate the force from images
The process to estimate the contact force can be summarized as: (a) continuum robot centerline detection; (b) compute the curvature feedback based on the detected centerline; and (c) estimate the contact force based on the curvature feedback. Here, we assume the continuum robot shape can be accurately identified via various image segmentation techniques [Reference Manakov, Kolpashchikov, Danilov, Nikita Vitalievich Laptev and Gerget37] or mounting active tracking coils on the continuum device [Reference Chen, Howard, Godage and Sengupta12, Reference Yue Chen, Wang, Kwong, Stevenson and Schmidt38]. Thus, we will skip the image segmentation step in this preliminary study. To obtain this ideal continuum robot shape from image feedback, we first deform the Nitinol tube with random force, overlay the deformed tube (Fig. 7(a)) on a 128 × 170 grid with the pixel resolution of 0.5 mm × 0.5 mm (which is the ultrasound imaging resolution), and then threshold the grid (as shown in Fig. 7(b)) to obtain Fig. 7(c). After obtaining continuum tube image, the centerline of the continuum robot, as presented in Fig. 7(d) can be detected. This will be achieved by the skeletonization algorithm proposed in refs. [Reference Kerschnitzki, Kollmannsberger, Burghammer, Duda, Weinkamer, Wagermaier and Fratzl39, Reference Lee, Kashyap and Chu40], which is well-accepted imaging processing algorithm in the field of computer vision. A sample continuum robot image and the corresponding result of the skeletonization algorithm are presented in Fig. 7(d). After detecting the centerline of the continuum robot, the curvature feedback of the robot can then be computed through (29). Finally, the contact force can be estimated by the curvature-based force estimation method by feeding the curvature feedback we computed.

Figure 7. (a) Shape of the deformed rod. (b) The blurred grid within the threshold. (c) The resulting image of the deformed rod. (d) Centerline (red pixels) detection using skeletonization algorithm.

Figure 8. Curvatures computed from the imaging.
4.2.2. Force estimation results
As presented in Fig. 8, the curvature feedback can be computed accurately from image data. This is a critical step for the curvature-based force estimation method. After obtaining the curvature feedback, we use them to estimate the force magnitudes and the corresponding locations. The step size of the integration of the ODEs for curvature calculation is
![]() $ds =$
1 mm. The results of the curvature-based force estimation are presented in Figs. 9 and 10. As summarized in Table III, the overall force magnitude estimation error is
$ds =$
1 mm. The results of the curvature-based force estimation are presented in Figs. 9 and 10. As summarized in Table III, the overall force magnitude estimation error is
![]() $0.049 \pm 0.048$
N and the overall location estimation error is
$0.049 \pm 0.048$
N and the overall location estimation error is
![]() $2.75 \pm 1.71$
mm. For single force estimation, the force magnitude estimation error is
$2.75 \pm 1.71$
mm. For single force estimation, the force magnitude estimation error is
![]() $0.045 \pm 0.040$
N and the location error is
$0.045 \pm 0.040$
N and the location error is
![]() $2.20 \pm 1.73$
mm. For double force estimation, the force magnitude estimation error is
$2.20 \pm 1.73$
mm. For double force estimation, the force magnitude estimation error is
![]() $0.051 \pm 0.048$
N and the location estimation error is
$0.051 \pm 0.048$
N and the location estimation error is
![]() $3.11 \pm 1.64$
mm. For triple force estimation, the force magnitude estimation error is
$3.11 \pm 1.64$
mm. For triple force estimation, the force magnitude estimation error is
![]() $0.050 \pm 0.037$
N and the location estimation error is
$0.050 \pm 0.037$
N and the location estimation error is
![]() $2.59 \pm 1.41$
mm. The result shows that the curvature-based method can estimate the force locations accurately for either single force or multiple force estimations. However, the force magnitude accuracy will be degraded if more forces are acting on the rod. Although moderate errors exist, this result validates the feasibility of applying curvature-based force estimation method with image data to estimate the contact force.
$2.59 \pm 1.41$
mm. The result shows that the curvature-based method can estimate the force locations accurately for either single force or multiple force estimations. However, the force magnitude accuracy will be degraded if more forces are acting on the rod. Although moderate errors exist, this result validates the feasibility of applying curvature-based force estimation method with image data to estimate the contact force.
Table III. Force estimation RMSE using image feedback.


Figure 9. Single force estimation result based on curvature computed from image. (a) Force magnitude estimation. (b) Force location estimation.

Figure 10. Experimental results for double and triple forces estimation based on image feedback. (a) Force magnitudes estimation. (b) Force locations estimation. During each experiment, the circle marker indicates the first force, diamond marker indicates the second force, and the triangle marker indicates the third force (triple force scenario).
5. Conclusions
In this article, we develop the curvature-based force estimation method to estimate the contact force magnitude and location. The proposed method was validated on a straight 290 mm Nitinol tube, with single or multiple forces acting at different locations. The curvature feedback was obtained from the multicore FBG sensors and the images. The results showed that the model can estimate the force magnitude and location accurately. For the curvature feedback obtained from multicore FBG sensors, the overall force magnitude estimation error is
![]() $0.062 \pm 0.068$
N and the overall location estimation error is
$0.062 \pm 0.068$
N and the overall location estimation error is
![]() $3.51 \pm 2.60$
mm. For the curvature feedback obtained from image, the overall force magnitude estimation error is
$3.51 \pm 2.60$
mm. For the curvature feedback obtained from image, the overall force magnitude estimation error is
![]() $0.049 \pm 0.048$
N and the overall location estimation error is
$0.049 \pm 0.048$
N and the overall location estimation error is
![]() $2.75 \pm 1.71$
mm.
$2.75 \pm 1.71$
mm.
However, the accurate force estimation relies on reliable curvature calculation of the deformed continuum robot. One of the main challenges for practical implementation is to accurately extract the center line from multiple images when robot is subjected to 3D deformation. 3D shape reconstruction may have larger noise or error caused by multicamera calibration. Moreover, computing the curvature from 3D reconstructed shape remains a challenging task. Therefore, our future work will involve the study of 3D contact force estimation, machine learning methods for curvature calculation, and evaluation of the force estimation performance in clinical settings with 3D image feedback such as 3D ultrasound and magnetic resonance imaging.
Author contributions
Qingyu Xiao, Xiaofeng Yang, and Yue Chen designed the study. Qingyu Xiao conducted data gathering. Qingyu Xiao and Yue Chen wrote the article.
Financial support
This research was partially funded by Georgia Institute of Technology Startup Grant.
Conflict of interest
Not applicable.
Ethical standards
Not applicable.