Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T04:59:17.341Z Has data issue: false hasContentIssue false
  • English
  • Français

An improved minimal error model for the robotic kinematic calibration based on the POE formula

Published online by Cambridge University Press:  20 September 2021

Ruiqing Luo Open the ORCID record for Ruiqing Luo [Opens in a new window] ,
Wenbin Gao ,
Qi Huang  and
Yi Zhang
Ruiqing Luo
Affiliation:
School of Mechanical Engineering, Anhui University of Technology, MA’Anshan, China Anhui Province Key Laboratory of Special Heavy Load Robot, MA’Anshan, China
Wenbin Gao*
Affiliation:
School of Mechanical Engineering, Anhui University of Technology, MA’Anshan, China Anhui Province Key Laboratory of Special Heavy Load Robot, MA’Anshan, China
Qi Huang
Affiliation:
School of Mechanical Engineering, Anhui University of Technology, MA’Anshan, China Anhui Province Key Laboratory of Special Heavy Load Robot, MA’Anshan, China
Yi Zhang
Affiliation:
State Key Laboratory of Robotics, Shenyang Institute of Automation, Chinese Academy of Sciences, Shenyang, China
*
*Corresponding author. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Summary

The conventional product of exponentials 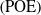$\left(\rm POE\right)$ -based methods dissatisfy the parametric minimality for the kinematic calibration of serial robots due to overlooking the magnitude and pitch constraints. Thus, the minimal kinematic model is presented to solve this problem, which can be developed further. This paper puts forward an improved algorithm for the minimal parameter calibration. An actual kinematic model with the minimal parameters 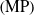$\left(\rm MP\right)$ is constructed according to the geometric properties of actual joint twists in the auxiliary frames established on the basis of the nominal joint axes. Then, the initial pose error is defined in the tool coordinate frame, which is expressed as the exponential map of the twist, and all twist descriptions are unified, so as to give a unified kinematic model in mathematics. By differentiating the kinematic model, a minimal error model is derived in explicit form. Subsequently, we propose a novel parameter identification method, which identifies the orientation error and position error parameters separately by the iterative least-squares method and updates the MP uniformly. Finally, the simulations and experiments on the different serial robots are conducted to verify the correctness and effectiveness of the proposed algorithm. The simulation results show our calibration algorithm outperforms the existing ones in the accuracy aspect, and the experiment result shows that the absolute pose accuracy of the UR5 industrial robot is upgraded about 9 times under a statistics sense after the calibration.

Keywords

Kinematic calibrationProduct of exponentials (POE)Parametrically minimalIdentification
Type
Research Article
Information
Robotica , Volume 40 , Issue 5 , May 2022 , pp. 1607 - 1626
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Yang, X. D., Wu, L., Li, J. Q. and Chen, K., “A minimal kinematic model for serial robot calibration using POE formula,” Robot. Cim.-Int. Manuf. 30, 326–334 (2014).CrossRefGoogle Scholar
Zhuang, H. Q. and Roth, Z. S., Camera-Aided Robot Calibration (CRC Press, FL, 1996).Google Scholar
Roth, Z., Mooring, B. and Ravani, B., “An overview of robot calibration,” IEEE J. Robot. Autom. 3(5), 377–385 (1987).CrossRefGoogle Scholar
Meggiolaro, M.A. and Dubowsky, S., “An Analytical Method to Eliminate the Redundant Parameters in Robot Calibration,” In: Proceedings of IEEE International Conference on Robotics $\&$ Automation (2000) pp. 3609–3615.Google Scholar
Schröer, K., Albright, S. L. and Grethlein, M., “Complete minimal and model-continuous kinematic models for robot calibration,” Robot. Cim.-Int. Manuf. 13(1), 73–85 (1997).CrossRefGoogle Scholar
Denavit, J. and Hartenberg, R. S., “A kinematic notation for lower-pair mechanisms based on matrices,” J. Appl. Mech.-T. AESM 22(6), 215–221 (1995).CrossRefGoogle Scholar
Hayati, S.A., “Robot Arm Geometric Link Parameter Estimation,” In: Proceedings of the 22th IEEE Conference on Decision $\&$ Control (1983) pp. 1477–1483.Google Scholar
Zhuang, H. Q., Roth, Z. S. and Hamano, F., “A complete and parametrically continuous kinematic model for robot manipulators,” IEEE T. Robot. Autom. 8(4), 451–463 (1992).CrossRefGoogle Scholar
Stone, H. W. and Sanderson, A. C., “Statistical performance evaluation of the S-model arm signature identification technique,” In: Proceedings of the IEEE International Conference on Robotics $\&$ Automation (1988) pp. 939–946.Google Scholar
Murray, R. M., Li, Z. X. and Sastry, S. S., A Mathematical Introduction to Robotic Manipulation (CRC Press, FL, 1994).Google Scholar
Okamura, K. and Park, F. C., “Kinematic calibration using the product of exponentials formula,” Robotica 14(4), 415–421 (1996).CrossRefGoogle Scholar
Chen, I.-M., Yang, G. L., Tan, C. T. and Yeo, S. H., “Local POE model for robot kinematic calibration,” Mech. Mach. Theory 36(11), 1215–1239 (2001).CrossRefGoogle Scholar
Lou, Y. J., Chen, T. N., Wu, Y. Q., Li, Z. B. and Jiang, S. L., “Improved and Modified Geometric Formulation of POE Based Kinematic Calibration of Serial Robots,” In: Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (2009) pp. 5261–5266.Google Scholar
He, R. B., Zhao, Y. J. and Yang, S. N., “Kinematic-parameter identification for serial-robot calibration based on POE formula,” IEEE T. Robot. 26(3), 411–423 (2010).CrossRefGoogle Scholar
Gao, W. B., Wang, H. G., Jiang, Y. and Pan, X. A., “Research on the calibration for a modular robot,” Journal of Mechanical Engineering 50(3), 33–40 (2014).CrossRefGoogle Scholar
Jiang, Z. Z., Gao, W. B. and Yu, X. L., “An improved robot calibration method using the modified adjoint error model based on POE,” Adv. Robot. 34(19), 1229–1238 (2020).CrossRefGoogle Scholar
Wang, W., Wang, G. and Yun, C., “A calibration method of kinematic parameters for serial industrial robots,” Ind. Robot 41(2), 157–165 (2014).CrossRefGoogle Scholar
Wu, L., Yang, X. D., Chen, K. and Ren, H. J., “A minimal POE-based model for robotic kinematic calibration with only position measurements,” IEEE T. Autom. Sci. Eng. 12(2), 758–763 (2015).CrossRefGoogle Scholar
Chen, G. L., Wang, H. and Lin, Z. Q., “Determination of the identifiable parameters in robot calibration based on the POE formula,” IEEE T. Robot. 121, 844–856 (2018).Google Scholar
Li, C., Wu, Y.Q., Löwe, H. and Li, Z. X., “POE-based robot kinematic calibration using axis configuration space and the adjoint error model,” IEEE T. Robot. 32(5), 1264–1279 (2016).CrossRefGoogle Scholar
Chang, C. G., Liu, J. G., Ni, Z. Y. and Qi, R. L., “An improved kinematic calibration method for serial manipulators based on POE formula,” Robotica 36(8), 1244–1262 (2018).CrossRefGoogle Scholar
Liu, H., Zhu, W. D., Dong, H. Y. and Ke, Y. L., “An improved kinematic model for serial robot calibration based on local POE formula using position measurement,” Ind. Robot 45(5), 573–584 (2018).CrossRefGoogle Scholar
Sun, T., Lian, B. B., Yang, S. F. and Song, Y. M., “Kinematic calibration of serial and parallel robots based on finite and instantaneous screw theory,” IEEE T. Robot. 36(3), 816–834 (2020).Google Scholar
Chen, G. L., Kong, L. Y., Li, Q. C., Wang, H., and Lin, Z. Q., “Complete, minimal and continuous error models for the kinematic calibration of parallel manipulators based on POE formula,” Mech. Mach. Theory 121, 844–856 (2018).CrossRefGoogle Scholar
Kong, L. Y., Chen, G. L., Wu, H., Huang, G. Y. and Zhang, D., “Kinematic calibration of a 3-PRRU parallel manipulator based on the complete, minimal and continuous error model,” Robot. Cim.-Int. Manuf. 71, 102158.1–102158.12 (2021).CrossRefGoogle Scholar
Evertt, L. J. and Hsu, T. W., “The theory of kinematic parameter identification for industrial robots,” J. Dyn. Syst.-T. ASME 110(1), 96–100 (1988).CrossRefGoogle Scholar
Wu, Y. Q., Li, C., Li, J. and Li, Z. X., “Comparative Study of Robot Kinematic Calibration Algorithms using a Unified Geometric Framework,” In: Proceedings of the IEEE International Conference on Robotics $\&$ Automation (2014) pp. 1393–1398.Google Scholar
Fu, Z. T., Dai, J. S., Yang, K., Chen, X. B. and Pablo, L. C., “Analysis of unified error model and simulated parameters calibration for robotic machining based on Lie theory,” Robot Cim.-Int. Manuf. 61, 101855.1–101855.14 (2020).CrossRefGoogle Scholar