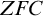WHAT IS A RESTRICTIVE THEORY?

Abstract

In providing a good foundation for mathematics, set theorists often aim to develop the strongest theories possible and avoid those theories that place undue restrictions on the capacity to possess strength. For example, adding a measurable cardinal to $ZFC$ is thought to give a stronger theory than adding $V=L$ and the latter is thought to be more restrictive than the former. The two main proponents of this style of account are Penelope Maddy and John Steel. In this paper, I’ll offer a third account that is intended to provide a simple analysis of restrictiveness based on the algebraic concept of retraction in the category of theories. I will also deliver some results and arguments that suggest some plausible alternative approaches to analyzing restrictiveness do not live up to their intuitive motivation.

Mmmm, standin’ at the crossroad,

I tried to flag a ride

Standin’ at the crossroad,

I tried to flag a ride

Didn’t nobody seem to know me,

everybody pass me by

$\ \ \ \ \ \ \ \ \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad $ Robert Johnson

1 The canonical example

Recall a well-known fork in the road. You’re using set theory as a foundation for mathematics and, as a good set theorist, you aim to provide a strong theory capable of answering some of the many seemingly reasonable questions left undecided by, say, $ZFC$ . In the course of your travels, you come across a couple of plausible contenders that you could consider admitting into your foundation: every set is constructible and there is a measurable cardinal. The first axiom enforces order on the universe while the latter delivers an object having far reaching consequences in analysis and beyond. Both axioms are worth taking seriously, but as Dana Scott perhaps sadly showed, we can only add one of them: $ZFC$ proves that if every set is constructible, then there are no measurable cardinals. Thus, we should choose one path over the other. But how? We shall call this the canonical example.

The following observation is frequently deployed at this point. $MC$ can interpret $V=L$ , but $V=L$ cannot interpret $MC$ . ¹ In other words, $MC$ can describe an inner model, known as L, in which all of the axioms of $V=L$ are true, but $V=L$ cannot do the same for $MC$ on pain of violating Gödel’s second incompleteness theorem. On (quite roughly) this basis, it has been argued that this tells us that: $MC$ has greater interpretability power than $V=L$ , and that $V=L$ is restrictive in comparison to $MC$ . ² In this paper, I want to provide a plausible formal analysis of what we mean when we say that one theory is restrictive in comparison to another. The motivation behind my approach is a very simple algebraic idea. Indeed, my goal is to keep the analysis as simple as possible. I’m not so much aiming to provide the definitive analysis of restrictiveness as highlight and delimit a very natural tool in this larger project.

Turning to the literature, the project to analyze restrictiveness in set theory has two major proponents: Penelope Maddy and John Steel. We now discuss some of the salient points of that work and then contextualize the current paper by drawing out some strategic differences between this project and those. In final chapters of [14], we find the development of a formal logical definition—based on interpretability—that aims to tell us when one theory maximizes over another. It is a tour de force in philosophy of set theory. It would take us too far afield to provide a full description of Maddy’s final definition along with the philosophy required to motivate it. However, a couple of important themes emerge in Maddy’s analysis that aim to cut to the core of restrictiveness and that warrant further discussion. The first of these is the idea that one theory is restrictive with respect to another if it is unable to talk about as much mathematics as the other. In the case of the canonical example, we might think of $V=L$ as restrictive in comparison to $MC$ since it is not able to talk about the real number $0^{\#}$ . ³ The second (arguably related) idea is that restrictive theories are unable to match unrestrictive theories. So in the canonical example, we might say that $V=L$ cannot match $MC$ in the sense that it cannot interpret $MC$ . ⁴ This is an extremely brief overview of a huge project; however, we’ll have cause to visit more specific parts of Maddy’s analysis throughout this paper. ⁵

In [5, 22], Steel provides an argument for accepting large cardinal axioms which leans on the notion of interpretative power of a theory. For Steel, maximizing interpretative power “entails maximizing formal consistency strength, but the converse is not true, as we want our interpretations to preserve meaning.” Steel does not provide a full description of what it means for an interpretation to preserve meaning, but the obvious candidates are the kinds of model construction used by set theorists to prove that various extensions of $ZFC$ are equiconsistent. These constructions come in two main flavors: inner models and generic extensions. Both approaches deliver models with the same natural numbers and ordinals: the interpretations differ from their ground models in being thicker or thinner. It will be important to note that Maddy does not admit generic extensions into her analysis and thus restricts her attention to inner models. ⁶ Returning to the canonical example, we then see that adopting $V=L$ is restrictive in comparison to $MC$ since it, “simply prevents us from asking as many questions, since we are forbidden to ask about the world outside L” [5]. We also note that Steel’s analysis is (deliberately) informal and thus more of a moving target.

The analysis I aim to provide in this paper will be distinguished from Maddy and Steel on a number of fronts. First, unlike Maddy but like Steel, I aim to admit generic extension as being on a par with inner model interpretation. I don’t intend to make a thorough argument for this admission here beyond noting that this appears to be the default position among contemporary set theorists. The admission of generic extensions provides opportunities to enrich the analysis of restrictiveness while adding some non-trivial technical hurdles that will frequently occupy us throughout this paper. Unlike Steel but like Maddy, I aim to provide a formal analysis of restrictiveness. Almost of necessity, this means that my definition will have shortcomings. We shall discuss these as they emerge; however, my approach will generally be to leave the analysis alone rather than attempt repair. My reason for this is that I think the simplicity and naturalness of the solution offered here warrants developing an understanding of both its capacities and limitations as an analysis of restrictiveness. Unlike Maddy but probably like Steel, I am going to claim that the ontology these theories appear to describe is not useful in the analysis of how one theory can talk about more mathematics than another. Unlike Steel, I am going to argue that meaning preservation is not particularly useful in the analysis of restrictiveness. Finally, in contrast with one of Maddy’s themes, I am going to claim that one plausible way of analyzing matching between theories is too weak to be of any use in comparing theories.

The paper is set out as follows. In Section 2, we describe the basic interpretative machinery required for comparing theories and then describe our target notion: retraction. This leads us to a preliminary analysis of restrictiveness that faces some fatal limitations for our project as described in Section 2.1. In particular, the preliminary analysis is not able to satisfactorily handle forcing arguments. These results appear to open up the field up into a messy plurality of different analyses. However, in Section 3, we show a number of analyses weaker than that offered in this paper suffer flaws that undermine the stories that motivate them. More specifically, we shall show that there are substantial hurdles for analyses that try to capture the ideas of: one theory representing more mathematics than another, and one theory being so strong as to be unmatchable by another. This is a long section and may be best skipped on an initial reading by those awaiting the exposition of the paper’s proposed approach. This is developed in Section 4, where we provide an account of restrictiveness based on what we call generic retraction. The majority of this section is devoted to setting up the basic theory, demonstrating alignment with intuitive cases, and then applying the theory to a couple of simple case studies.

2 The retraction response

The main instrument in our analysis is the theory of relative interpretability. ⁷ In this paper, we’ll restrict our attention to theories in the language $\mathcal {L}_{\in }$ of set theory consisting of a single one-place relation symbol $\in $ . An interpretation is a translation t from the formulae of the language of set theory to itself, which is based on definitions giving a domain and interpretation for the membership relation. More specifically, we have two formulae $\delta _{t}(x)$ and $\varepsilon _{t}(x)$ of $\mathcal {L}_{\in }$ and define t recursively on formulae as follows:

This then gives us our fundamental definition for theory comparison.

Definition 1. For theories T and S, we say that T interprets S if there is some interpretation t such that for all sentences $\varphi $ of $\mathcal {L}_{\in }$

$$ \begin{align*} S\vdash\varphi\ \Rightarrow\ T\vdash t(\varphi). \end{align*} $$

The underlying mechanism works since t essentially defines an internal model of S within any model of T. We now use a little category theory to describe this more formally. For T a theory in $\mathcal {L}_{\in }$ , let $mod(T)$ be the category whose objects are models $\mathcal {M}$ of T and whose arrows are elementary embeddings $j:\mathcal {M}\to \mathcal {N}$ between them. Then it can be seen that an interpretation t determines a functor $t^{*}:mod(T)\to mod(S)$ . This is done by taking a model $\mathcal {M}$ of T and taking the model defined inside $\mathcal {M}$ by $\delta _{t}$ and $\varepsilon _{t}$ . ⁸ Let us call the functors determined in this way by interpretations, mod-functors, and let us abuse notation and write t instead of $t^{*}$ . We then note the following fundamental theorem of interpretability.

Theorem 2. Suppose T interprets S via t. Then for all models $\mathcal {M}$ of T and sentences $\varphi $

$$ \begin{align*} \mathcal{M}\models t(\varphi)\ \Leftrightarrow\ t(\mathcal{M})\models\varphi. \end{align*} $$

This semantic and category theoretic approach allows for more intuitive reasoning about the relationships between theories. For example, we see that T interprets S just in case there is some mod-functor $t:mod(T)\to mod(S)$ . Let us say that T and S are mutually interpretable if there are interpretations t and s witnessing that T interprets S and S interprets T. We shall denote this situation by writing $t:mod(T)\leftrightarrow mod(S):s$ .

This puts us in position to provide the core definition of this paper.

Definition 3. We say that $mod(T)$ is a retract of $mod(S)$ if there are mod-functors $t:mod(T)\leftrightarrow mod(S):s$ witnessing mutual interpretability such that the following diagram commutes:

We say that t is a section and s is a retraction. We shall frequently just say T is a retract of S.

Of course, this is a very familiar algebraic relationship. It just says that t has a left inverse. Nonetheless, I think that the simplicity can be a little misleading and it’s also very easy to forget the names. With this in mind, I’ll attempt a more palpable description. Suppose that I, Toby, go to a restaurant owned by my friend Simon. It’s the dead of Winter on a cold night, but it’s toasty warm when I get inside the restaurant. The waiter sees that I am now overdressed and kindly offers to take my coat into the care of Simon’s restaurant. I then have a lovely meal with some colleagues and after I have paid the bill, I ask the waiter to return my coat. Happily, the coat is returned in exactly the same condition I deposited it. Thus if we squint a little, I am in the position of the retract, T. I deposit my coat at Simon’s restaurant, S, as though following the t functor, and then the s functor returns the coat which we see is unchanged since t and s compose to the identity. Importantly, my ability to enjoy the use of my coat has not been restricted by Simon’s restaurant. But suppose, I had instead gone to a different restaurant that is short-staffed and cheap, if not cheerful. Then having deposited my coat the beginning of the meal, I might find that I am returned a different coat or no coat at all. Clearly, the former situation is preferable to the latter where something has been lost.

We now apply this idea to a version of our canonical example. The first thing to note is that a necessary condition for a retraction between two theories is that those theories must be mutually interpretable. This rules out a comparison between $V=L$ and $MC$ and so there could appear to be some restriction in scope. Nonetheless, it is relatively trivial to generalize our analysis to theories that are not mutually interpretable, but we defer that until Section 4.2 after some helpful results from Section 3.2 are on the table. But even in the restricted setting there is also a sense in which it gives us better information. We aim be able to show that $V=L$ is restrictive with respect to $ZFC$ alone, i.e., without needing to compare with the stronger axiom that there is a measurable cardinal. Thus, this method will allow us to see that $V=L$ is itself a restrictive addition to $ZFC$ .

Theorem 4. (1) $V=L$ is a retract of $ZFC$ .

(2) $ZFC$ is not a retract of $V=L$ , if there is a transitive model of $V=L$ .

Informally, (1) tells us that there is a linguistic procedure via which we can deposit a model of $V=L$ among the models of $ZFC$ and then have exactly the same model returned. On the other hand, (2) tells us that there is no uniform way of depositing the models of $ZFC$ among the models of $V=L$ and ensuring that the same model is returned. Some information is always lost. The following (quite detailed) proof outlines a strategy that will recur throughout this paper.

Proof. (1) Let $i:mod(V=L)\to mod(ZFC)$ be the inclusion map and let $l:mod(ZFC)\to mod(V=L)$ be given by restricting quantifiers to L. Then it is easy to see that if $\mathcal {M}$ is a model of $V=L$ , then

$$ \begin{align*} l\circ i(\mathcal{M})=l(\mathcal{M})=L^{\mathcal{M}}=\mathcal{M}. \end{align*} $$

(2) Suppose toward a contradiction that $s:mod(ZFC)\leftrightarrow mod(V=L):t$ are mod-functors such that for all models $\mathcal {M}$ of $ZFC$ , $t\circ s(\mathcal {M})=\mathcal {M}$ . Using our assumption, fix the transitive model $L_{\mu }$ where $\mu $ is least such that $L_{\mu }\models V=L$ . Let M be a generic extension of $L_{\mu }$ by a Cohen real. Then M is a transitive model of $ZFC$ with $Ord^{M}=\mu $ .

Let N be the transitive collapse of the well-founded part of $s(M)$ . Suppose $Ord^{N}<\mu $ . Then $s(M)$ must be ill-founded since $\mu $ is least such that $L_{\mu }\models V=L$ . But then $s(M)$ can only define ordinals of length up to $\mu $ . This is a contradiction since $s(M)$ must be able to define a well-ordering of length $Ord^{t\circ s(M)}=Ord^{M}=\mu $ .

Suppose $Ord^{N}=\mu $ . If $s(M)$ is ill-founded, then we get a similar contradiction, since $s(M)$ can define $Ord^{t\circ s(M)}=\mu $ which is impossible. So suppose $s(M)$ is well-founded. Then we have

$$ \begin{align*} s(M[g])\cong L_{\mu}=N. \end{align*} $$

But then we have a model $s(M)$ of $V=L$ that can collapse what it thinks is the well-founded, extensional and set-like proper class model $t\circ s(M)$ of $V=L[c]$ , which is impossible.

Suppose $Ord^{N}>\mu $ . Then $\mu $ is definable as a set in $s(M)$ and so is $t\circ s(M)$ . But this means that $s(M)$ can define a truth predicate, $Tr^{*}$ , for $t\circ s(M)\equiv M$ ; thus, we have

$$ \begin{align*} M\models\varphi\ \Leftrightarrow\ s(M)\models Tr^{*}\ulcorner\varphi\urcorner, \end{align*} $$

where $\ulcorner \cdot \urcorner $ is an arithmetic coding of $\mathcal {L}_{\in }$ . Moreover, this truth predicate can also be defined in M, which is impossible. More specifically, we see that for all sentences $\varphi $ in $\mathcal {L}_{\in }$

$$ \begin{align*} M\models\varphi & \Leftrightarrow t\circ s(M)\models\varphi\\ & \Leftrightarrow s(M)\models Tr^{*}\ulcorner\varphi\urcorner\\ & \Leftrightarrow M\models s(Tr^{*}\ulcorner\varphi\urcorner). \end{align*} $$

We then note that there is a formula $\tau (x)$ in $\mathcal {L}_{\in }$ such that $\tau (x)$ is equivalent to $s(Tr^{*}(x))$ in any $\omega $ -model. Then $\tau (x)$ is a truth predicate for M which is definable in M contradicting Tarski’s theorem.

Beyond the metaphors of deposit and return, the following proposition highlights the value of retraction in comparing theories.

Proposition 5. (1) If T is a retract of S as witnessed by $t:mod(T)\leftrightarrow mod(S):s$ , then for any $T^{+}\supseteq T$ , there is some $S^{+}\supseteq S$ such that t and s witness that $T^{+}$ is a retract of $S^{+}$ .

(2) Suppose S can interpret T, but T is not a retract of S. Then there is no $\varphi $ such that T is a retract of $S\cup \{\varphi \}$ .

Informally (1) tells us that the procedure ensuring deposit and return succeeds can continue to be used no matter how we strengthen the theory making the deposit. On the other hand, (2) tells us that if something is lost when we try to deposit models of T in models of S, then there is no sentence we can add to S that will repair the relationship. Among other things, this tells us that there is no finite extension of $V=L$ such that $ZFC$ is a retract of $V=L$ .

Proof. (1) Fix mod-functors t and s witnessing that T is a retract of S. Then given $T^{+}\supseteq T$ , we let

$$ \begin{align*} S^{+}=\{s(\varphi)\ |\ \varphi\in T^{+}\}. \end{align*} $$

Let $\mathcal {M}$ be a model of $T^{+}$ , then since $\mathcal {M}$ is already a model of T, we see that $s\circ t(\mathcal {M})=\mathcal {M}$ , so we just need to show that $t(\mathcal {M})$ is a model of $S^{+}$ . To see this observe that for all $\varphi $

$$ \begin{align*} \mathcal{M}\models\varphi & \Leftrightarrow s\circ t(\mathcal{M})\models\varphi,\\ & \Leftrightarrow t(\mathcal{M})\models s(\varphi), \end{align*} $$

and since $\mathcal {M}\models T^{+}$ , we see $t(\mathcal {M})\models S^{+}$ .

(2) Suppose toward a contradiction that T is not a retract of S, but T is a retract of $S\cup \{\varphi \}$ for some $\varphi $ . Then fix mod-functors $t:mod(T)\leftrightarrow mod(S\cup \{\varphi \}):s_{0}$ witnessing this. Using the assumption that S can interpret T, fix a mod-functor $s_{1}:mod(S)\to mod(T)$ . Let s be the mod-functor $s:mod(S)\to mod(T)$ obtained by using $s_{0}$ in models where $\varphi $ holds, and using $s_{1}$ where it does not. Then it is easy to see that t and s witness that T is a retract of S, which is impossible.

This brings us to our first, provisional definition of restrictiveness. ⁹ Let us say that T is restrictive with respect to S if:

1. (1) T is a retract of S; but

2. (2) S is not a retract of T.

Thus, $V=L$ is restrictive with respect to $ZFC$ . Beyond the canonical example, we can see that this approach lines up quite well with what we’d expect from a definition of restrictiveness. First, we introduce a little notation. Let our axioms for $ZFC$ include set-induction, the well-ordering theorem and the collection schema. ¹⁰ Let $ZFC\backslash \{Inf\}$ be $ZFC$ without the axiom of infinity. Let $ZFC_{fin}$ be $ZFC\backslash \{Inf\}$ plus the negation of the axiom of infinity. Let $ZFC\backslash \{\mathcal {P}\}$ be $ZFC$ without the axiom of powerset. Let $ZFC_{count}$ be $ZFC\backslash \{\mathcal {P}\}$ plus the statement that every set is countable, $\forall x\ |x|=\omega $ .

Proposition 6. Suppose there is a transitive model of $ZFC$ . Then:

(1) $ZFC_{fin}$ is restrictive with respect to $ZFC\backslash \{Inf\}$ .

(2) $ZFC_{count}$ is restrictive with respect to $ZFC\backslash \{\mathcal {P}\}$ .

In each of these cases, we consider the addition of an axiom which seem obviously restrictive: there are no infinite sets and there are no uncountable sets. This is quite encouraging.

Proof. (1) Let $i:mod(ZFC_{fin})\to mod(ZFC\backslash \{Inf\})$ be inclusion map, and let $f:mod(ZFC\backslash \{Inf\})\to mod(ZFC_{fin})$ be functor resulting from restricting quantifiers to $V_{\omega }$ . i and f clearly witness a retraction. To see that $ZFC\backslash \{Inf\}$ is not a retraction of $ZFC_{fin}$ , suppose toward a contradiction that it is and fix mod-funtors $s,t$ such that

$$ \begin{align*} s\,{:}\,mod(ZFC\backslash\{Inf\})\leftrightarrow mod(ZFC_{fin}):t, \end{align*} $$

where $t\circ s(\mathcal {M})=\mathcal {M}$ for all $\mathcal {M}\in mod(ZFC\backslash \{Inf\})$ . Let M be a transitive model of $ZFC$ and thus $Ord^{M}>\omega _{1}^{CK}$ . Then $s(M)$ is a model of $ZFC_{fin}$ . If $s(M)$ is not an $\omega $ -model, then it cannot define any $\omega $ -models including the $\omega $ -model $t\circ s(M)=M$ ; so suppose $s(M)$ is an $\omega $ -model. Then $s(M)\cong \langle V_{\omega },\in \rangle $ can define an ordinal of length $>\omega _{1}^{CK}$ , which is impossible. ¹¹

(2) Let $i:mod(ZFC_{count})\to mod(ZFC\backslash \{\mathcal {P}\})$ be the inclusion map, and let $h:mod(ZFC\backslash \{\mathcal {P}\})\to mod(ZFC_{count})$ be the functor resulting from restricting quantifiers to the hereditarily countable sets. Clearly these functors witness a retraction. To see that $ZFC\backslash \{\mathcal {P}\}$ is not a retraction of $ZFC_{count}$ , suppose

$$ \begin{align*} s:mod(ZFC\backslash\{\mathcal{P}\})\leftrightarrow mod(ZFC_{count}):t, \end{align*} $$

where $t\circ s(\mathcal {M})=\mathcal {M}$ for all $\mathcal {M}\in mod(ZFC\backslash \{\mathcal {P}\})$ . Let M be a transitive model of $ZFC$ . Let N be the result of taking the collapse of $s(M)$ in M. This is what M thinks is the well-founded, set-like part of $s(M)$ . Now suppose N is bounded in M and so N is represented as a set in M. But then N cannot define a well-ordering of length $Ord^{M}=Ord^{t\circ s(M)}$ , which is a contradiction. So suppose N is unbounded in M. The it can be seen that N thinks that every set in N is countable. But this is impossible. To see this consider $\omega _{1}^{M}$ which is also an element of N. Then we see that there is some surjection $f:\omega \to \omega _{1}^{M}$ in N. But $N\subseteq M$ , so M thinks $\omega _{1}^{M}$ is countable.

2.1 Hurdles

Taking a little stock, we now have a preliminary analysis of restrictiveness that lines up well with a number of simple cases that involve what seems to obviously be a restrictive axiom. However, celebration would be premature as we have yet to consider an example that uses forcing. The examples above all rely on models that are defined as submodels of ground models: internal models. Generic extension, however, allows us to define models that extend beyond ground models using a parameter that does not exist in the ground model: outer models. As we discussed above, like Steel, our goal in this paper is to incorporate forcing as a legitimate means of identifying relations, like restrictiveness, between alternative set theories. This issue will guide us below.

Our plan for this section is as follows. We shall identify a plausible pair of theories such that—if we are incorporating generic extensions into our account—they are so close to each other that neither should be regarded as restrictive with respect to the other. We then show that our preliminary analysis of restrictiveness fails to recognize the closeness of their relationship. This leads us to consider the prospects of using a coarser grained analysis of relationships between theories. From there we discuss one of our preferred solutions and set up the arguments of Section 3, which aim to show why weaker relationships are unable to provide the information we want.

Consider the theory extending $ZFC$ with the statement that the universe is a generic extension of L by a Cohen real. Let us write this as $V=L[c]$ . Let us consider how we might compare $V=L$ to $V=L[c]$ . Allowing generic extension into the picture, it seems that these theories are very closely related. To get from a model of $V=L[c]$ to a model of $V=L$ , we just need to go to its version of L. And to get from a model of $V=L$ to a model of $V=L[c]$ , we just need to take a generic extension of that model by a Cohen real. ¹² We’ll look at this in more detail below, but the main point is that this looks like the ideal test case for generic extension. If an analysis of restrictiveness is going to successfully incorporate generic extension, then—at a minimum—it will have to say that $V=L$ and $V=L[c]$ are not restrictive with respect to each other. Our current account does not show this:

Theorem 7 (Essentially [2])

$V=L[c]$ is not a retract of $V=L$ . ¹³

Very informally, this tells us that we cannot uniformly squeeze the models of $V=L[c]$ into the models of $V=L$ and then extract them in such a way that we are guaranteed to recover the model we started with. This way of putting things makes it sound as though $V=L$ is restrictive with respect to $V=L[c]$ . Thus since our goal is to incorporate generic extension, we must revise our analysis of restrictiveness. Given the dependence of our definition on retraction and interpretation, the natural place to look is among generalizations of these relationships. The following definition outlines a hierarchy of retraction relationships emerging from [24].

Definition 8. Let theories T and S be mutually interpretable via mod-functors $t:mod(T)\leftrightarrow mod(S):s$ . Then we say:

1. (1) T is a identity-retract of S if $\mathcal {M}=s\circ t(\mathcal {M})$ for all $\mathcal {M}\models T$ ;

2. (2) T is an isomorphism-retract of S if $\mathcal {M}\cong s\circ t(\mathcal {M})$ for all $\mathcal {M}\models T$ ; ¹⁴

3. (3) T is an elementary-retract of S if $\mathcal {M}\equiv s\circ t(\mathcal {M})$ .

We say that T is faithfully interpreted by S if there is some $s:mod(S)\to mod(T)$ that is a surjection up to elementary equivalence. ¹⁵

Clearly, an identity-retract is what we have been calling a retract above. An isomorphism-retract is then a weakening of ordinary retraction whereby we merely demand that the mod-functors associated with the retraction take us back to a model isomorphic to the one we started with, rather than exactly the same one. In mathematical contexts, we arguably only care about identity of objects up to isomorphism so perhaps little is lost by using this weaker relationship. Similarly, an elementary-retract occurs when taking the composition of the mod-functors takes us to a model that is elementary equivalent to the model we started with. So although we may be in a structurally distinct model, there is no sentence of our language that can pin down this distinction. Finally, we include faithful interpretation, which is not a retraction. We’ve defined it above semantically, but it has an equivalent syntactic form that tells us that S is able to prove exactly the sentences $s(\varphi )$ where T proved $\varphi $ . ¹⁶ There is thus a clear sense in which s allows S to provide an exact—so to speak—simulation of T. For this reason, it has been thought that the ability to provide a faithful interpretation provides significant information about the relationship between two theories. We shall argue against this in Section 3.2. The point of this is that we have now described some coarser-grained relationships between theories that can be motivated by plausible philosophical considerations. So this then brings us to the question: how and where does our test case of $V=L$ and $V=L[c]$ fit in this hierarchy of theoretical relationships? The following theorem answers this question.

Theorem 9. (1) $V=L[c]$ is an elementary-retract of $V=L$ .

(2) $V=L[c]$ is not an isomorphism-retract of $V=L$ , if there is a transitive model of $V=L$ .

Proof. (1) Let $s:mod(V=L[c])\to mod(V=L)$ be the mod-functor obtained by restricting quantifiers to L. Clearly $s(\mathcal {M})\models V=L$ for all models $\mathcal {M}$ of $V=L[c]$ . In the other direction, we define the mod-functor $t:mod(V=L)\to mod(V=L[g]$ ) as follows. Let $\mathcal {M}$ be an arbitrary model of $V=L$ . Let $\mathbb {B}$ be the completion of $2^{<\omega }$ and let U be the L-least ultrafilter on $\mathbb {B}$ . Working in $\mathcal {M}$ we then note that there are definable internal models $\bar {V},\bar {V}[G]$ and a set G with an elementary embedding $i_{U}$ such that

$$ \begin{align*} i_{U}:V\prec\bar{V}\subseteq\bar{V}[G], \end{align*} $$

where G is $i_{U}(\mathbb {B})$ generic over $\bar {V}$ and $\bar {V}[G]$ is a generic extension of $\bar {V}$ by G. ¹⁷ Let $t(\mathcal {M})$ be $\bar {V}[G]$ . $\bar {V}[G]$ satisfies the statement that its universe is a generic extension of $\bar {V}$ by a Cohen real. Moreover, $\bar {V}$ satisfies $V=L$ , so see that $t(\mathcal {M})$ is a model of $V=L[c]$ . Thus, we see that s and t witness mutual interpretability.

We now claim that $t\circ s(\mathcal {M})\equiv \mathcal {M}$ for all models $\mathcal {M}$ of $V=L[c]$ . Letting $\mathcal {M}\models V=L[c]$ , we see that $s(\mathcal {M})=L^{\mathcal {M}}$ and—using the notation from our definition of t— $t\circ s(\mathcal {M})=(\bar {V}[G])^{L^{\mathcal {M}}}$ . We then observe that for $\varphi $ an arbitrary sentence of $\mathcal {L}_{\in }$ that

$$ \begin{align*} \mathcal{M}\models\varphi & \Leftrightarrow L^{\mathcal{M}}\models“\Vdash_{\mathbb{B}}\varphi ”\\ & \Leftrightarrow(\bar{V})^{L^{\mathcal{M}}}\models“\Vdash_{i_{U}(\mathbb{B})}\varphi”\\ & \Leftrightarrow(\bar{V}[G])^{L^{\mathcal{M}}}\models\varphi\ \Leftrightarrow\ t\circ s(\mathcal{M})\models\varphi, \end{align*} $$

where the first and third biconditionals exploit the homogeneity of $\mathbb {B}$ . ¹⁸

(2) Suppose toward a contradiction that $mod(V=L[c])$ is a retract of $mod(V=L)$ and fix mod-functors $i,j$ such that

$$ \begin{align*} j:mod(V=L[c])\leftrightarrow mod(V=L):i \end{align*} $$

and $i\circ j(\mathcal {M})\cong \mathcal {M}$ for all models $\mathcal {M}$ of $V=L[c]$ . Let $L_{\mu }$ be the transitive model of $V=L$ for least $\mu $ . Let M be an extension of $L_{\mu }$ be a Cohen real. Let $\beta $ be the order type of the well-founded part of $j(M)$ . We show that every possible relation between $\mu $ and $\beta $ leads to a contradiction. However, first note that since $i\circ j(M)$ is definable in $j(M)$ , we see that $\mu $ is definable up to isomorphism in $j(M)$ . Suppose $\beta <\mu $ . Then $j(M)$ must be ill-founded by the minimality of $\mu $ . But then $j(M)$ cannot define $\mu $ : contradiction. Suppose $\beta =\mu $ . If $j(M)$ was ill-founded, then this would imply that $j(M)$ could define its well-founded part which is impossible. So suppose $j(M)$ is well-founded. Then we see that

$$ \begin{align*} j(M)\cong L_{\mu} \end{align*} $$

and so $j(M)$ and $i\circ j(M)$ have ordinals with the same order type. But this means we have a model $j(M)$ of $V=L$ that can collapse what it thinks is the well-founded, extensional and set-like proper class model $i\circ j(M)$ of $V=L[c]$ which is impossible. Suppose $\beta>\mu $ . Let $\dot {\mu }$ be the $j(M)$ -ordinal which is isomorphic to $\mu $ , which is definable in $j(M)$ . Then we see that $j(M)$ thinks that $i\circ j(M)$ is a set and so may define a truth predicate for $i\circ j(M)$ which can also be define in M, contradicting Tarski’s theorem.

Remark. Note that it is also easily seen by an argument similar to that used in part (1) of Theorem 4 that $s\circ t(\mathcal {N})\equiv \mathcal {N}$ for all models $\mathcal {N}$ of $V=L$ . Thus, $V=L$ and $V=L[c]$ are, in fact, sententially equivalent. It is also easy to see that this result generalizes to arbitrary definable homogeneous forcings.

The result above provides a helpful guide toward solving our main problem. It tells us that for our purposes, isomorphism-retracts are too strong and that relationships at or below elementary-retracts are a natural place to investigate. We shall see in Section 4 that elementary retracts also face problems ¹⁹ but our goal now is to investigate the hierarchy further in search of the sweet spot for our project.

3 Things that don’t work

In this section, we’ll argue that going strictly below the level of elementary-retracts is too coarse-grained to contribute to a plausible analysis of restrictiveness. Then in Section 4, we’ll take a closer look at elementary-retracts and their limitations before proposing a more tractable alternative. We’ll argue for the claim of this section by providing a series of results that demonstrate that various analyses of restrictiveness using notions weaker than elementary-retraction fail to live up to their intuitive motivation. In particular, we shall argue for three main claims. First, maximizing our ability to talk about mathematics is not well tracked by comparing the isomorphism types of the structures represented in one theory with that of another. Second, faithful interpretability is so easy to obtain that theories satisfying this relationship bear little or no intuitively interesting relationship with each other. And finally, we shall argue that strengthening faithful interpretability by restricting the class of acceptable models does not help matters. This is a long section that performs an important role; however, the reader who is more interested in exploring restrictiveness in the context of generic extensions should be able to safely skip ahead to Section 4.

3.1 More math and isomorphism

In [14], we find a way of analyzing restrictiveness that is concerned with the ability of a theory to represent mathematics. We might think of theory T being restrictive in relation to S if theory S is able to talk about more mathematics than T. This is a very sensible idea which prompts the more difficult question of how to devise a precise means to ascertain when this relationship holds. Maddy offers an analysis that aims to track the isomorphism types of structures represented by theories.

Our informal idea was that $ZFC+`0^{\#}\text { exists}$ ’ delivers a new isomorphism type because it proves the existence of a structure that is not isomorphic to anything constructible, that is, to anything in L. ([14, p. 221])

Maddy’s approach is to compare the isomorphism types represented by one theory with another. But this raises a difficulty. We are trying to compare the syntactic objects that are theories using the semantic ²⁰ objects which are the structures represented by these theories. It is not obvious that there is a clearly right way to do this. ²¹ Maddy deals with this by considering theories where one theory T interprets another theory S via some mod-functor t. We then ask if it is the case that in all models $\mathcal {M}$ of T, $\mathcal {M}$ thinks there is an isomorphism type witnessed in $\mathcal {M}$ that is not in its internal model $t(\mathcal {M})$ of S. If there is, then we are to think that S is restrictive. In theories extending $ZFC$ , we can simplify the description of this relationship to the following: ²²

Definition 10. (Essentially [14])

For theories T and S extending $ZFC$ , S is restrictive in relation to T if there is a mod-functor $t:mod(T)\to mod(S)$ such that for all $\mathcal {M}\models T$ , $\mathcal {M}$ thinks $t(\mathcal {M})$ is a proper inner model of $\mathcal {M}$ ; i.e., $t(\mathcal {M})\subsetneq \mathcal {M}$ . ²³

I’d like to claim that if this analysis fits with its motivation, then the relation of restrictiveness should be asymmetric. Recall that the S is supposed to be restrictive in relation to T if T is able to talk about (properly) more mathematics than S. Thus, if S cannot talk about as much mathematics as T, then it shouldn’t be the case that T also cannot talk about as much mathematics as S. But there is a problem for this plan. First recall the following fact.

Fact 11. If $V=L[U]$ and U is a normal measure on $\kappa $ , then $GCH$ holds. ²⁴

Using this we can then see that:

Proposition 12. $ZFC+\exists MC+GCH$ and $ZFC+\exists MC+\neg GCH$ are mutually inner model interpretable. ²⁵

Proof. Let M be a model of $ZFC+\exists MC+\neg GCH$ . Let $\kappa $ be the least measurable cardinal according to M and U be an M-normal ultrafilter on $\kappa $ . Then by Fact 11, $L[U]^{M}$ is an internal model satisfying $ZFC+MC+GCH$ . In the other direction, let M be a model of $ZFC+\exists MC+GCH$ . First we show that M has a definable inner model with a definable normal ultrafilter. Working in M, fix the least measurable cardinal $\kappa $ . Recall that for any normal measures $U_{0},U_{1}$ on $\kappa $ , we have $L[U_{0}]=L[U_{1}]$ . Thus, we may define $M^{*}$ in M as $L[U]^{M}$ , the inner model constructible from any M-normal measure U on $\kappa $ . ²⁶ And we may also define $U^{*}$ in M as $M^{*}\cap U$ for any normal measure U on $\kappa $ . Let $j:M^{*}\to Ult(M^{*},U^{*})=N$ be the ultrapower map as defined in $M^{*}$ .

Let $\mathbb {P}$ be $Add(\kappa ^{+},\kappa ^{+++})^{N}$ , i.e., the set of partial functions from $\kappa ^{+++}$ to $2$ with cardinality less than $\kappa ^{+}$ according to N. Since $GCH$ holds in $M^{*}$ and N, we see that for all $i\in \omega $

$$ \begin{align*} (\kappa^{+})^{M^{*}}=(\kappa^{+})^{N}\leq(\kappa^{+++})^{N}<j(\kappa)<((2^{\kappa})^{+})^{M^{*}} \end{align*} $$

and that

$$ \begin{align*} |\mathbb{P}|^{M^{*}}=|\mathcal{P}(\mathbb{P})^{N}|^{M^{*}}=(\kappa^{+})^{M^{*}}. \end{align*} $$

We then observe that $M^{*}$ thinks that $\mathbb {P}$ is $(\kappa ^{+})^{M^{*}}$ -closed. To see this suppose $f:s\to 2$ where $s\in \mathcal {P}(\kappa ^{+++})\cap N$ with $|s|<(\kappa ^{+})^{N}=(\kappa ^{+})^{M^{*}}$ . Now fix an injection $g:s\to \kappa $ with $g\in N$ . Then since $M^{*}$ thinks $^{\kappa }N\subseteq N$ , we see that $f\circ g^{-1}\in N$ and so $f\in N$ .

We then claim that a $\mathbb {P}$ -generic g for N exists in $M^{*}$ . To see this we work in $M^{*}$ . Let $\langle A_{\alpha }\rangle _{\alpha \in \kappa ^{+}}$ be an enumeration of the maximal anti-chains of $\mathbb {P}$ from N. Note that this enumeration will not be in N. Let $p_{0}$ be an arbitrary element of $\mathbb {P}$ . Let $p_{\alpha +1}$ be some $p\leq p_{\alpha }$ with $p_{\alpha +1}\in A_{\alpha }$ . And let $p_{\lambda }=\bigcup _{\alpha <\lambda }p_{\alpha }$ when $\alpha $ is a limit. This construction is well-defined since there are $(\kappa ^{+})^{M^{*}}$ many anti-chains in $\mathbb {P}$ and $M^{*}$ thinks that $\mathbb {P}$ is $(\kappa ^{+})^{M^{*}}$ closed. Let $g=\bigcup _{\alpha <2^{\kappa }}p_{\alpha }$ . Let $g^{*}$ be the $L[U^{*}]$ -least such generic.

Finally, we observe that $N[g^{*}]$ is a definable inner model of $M^{*}$ that satisfies $\neg GCH$ since in $N[g^{*}]$ we have $2^{(\kappa ^{+})}=(\kappa ^{+})^{++}$ . Moreover, it is clear that $g^{*}$ adds no new subsets of $\kappa $ to N and so $U^{*}$ is still a normal measure on $\kappa $ in $N[g^{*}]$ as required.

The upshot of this is that if one analyzes the idea of “more mathematics” as the ability to provide more isomorphism types, and one analyzes more isomorphism types as providing proper inner model interpretations, then we end up with a more than relation which is not asymmetric. I think this is a significant problem for this approach to analyzing what “more mathematics” means. I think the correct diagnosis for why this problem emerges is the mismatch of syntactic and semantic objects used in undertaking this analysis. I must note, however, that Maddy takes a different tack and builds asymmetry into the relation by saying that a theory T is properly restrictive with respect to theory S if T is restrictive with respect to S and S is not restrictive with respect to T. ²⁷ This certainly obtains an asymmetric relation but for the reasons outlined above, I think this fix is too ad hoc for the problem to hand.

3.2 Matching is cheap

In this section, I am going to use a sequence of examples to show that three related ideas for analyzing restrictiveness are ineffective. The first of these is motivated by our remarks above that isomorphism-retraction appears to be too fine-grained to be useful here. However, there are still many relationships to explore below this. In particular, we might consider faithful interpretability as a benchmark and thus avoid the retraction hierarchy altogether. Recall, the following proposition:

Proposition 13. T faithfully interprets S iff there is some translation t such that for all $\varphi \in \mathcal {L}_{S}$

$$ \begin{align*} S\vdash\varphi\ \Leftrightarrow\ T\vdash t(\varphi). \end{align*} $$

Informally, we see that T provides an exact simulation of S using the translation t. We might wonder if we could use this to make a story about restrictiveness that is analogous to our analysis via retraction. For example, we might be tempted to say that when T faithfully interprets S, it is able to represent the information of S without loss (or gain). This could be construed as analogous to when we know that S is a retract of T, we know that T is able to take the models of S into models of T and return them without loss. ²⁸ I aim to show that faithful interpretability is too weak to be of any real assistance for our project.

The second idea is based on the thought that a restrictive theory S might be so weak in comparison to some theory T that it cannot even be strengthened to match theory T in the sense of, say, providing an interpretation of it. In the context of retraction, a couple of salient results in this area occur in Proposition 5. More generally, I suspect the motivation behind this idea lies in the hierarchy theorems of computability theory and descriptive set theory.

For example, one might observe that faithful interpretation is essentially another way of saying that there is a particular kind of 1-reduction of the interpreted theory to the interpreting theory. And if we move over to the context of computability, we see that there are sets of naturals $A,B\subseteq \omega $ such that A is not 1-reducible to B and further no strengthening $A^{*}\subseteq A$ is 1-reducible to B either. ²⁹ If this kind of example could be generalized to theories, we would have a theory T than cannot faithfully interpret S and such that T cannot even be extended to do so. In such a situation, we might say that T cannot match S. Something like this idea appears in Maddy’s definition of strong maximization. ³⁰

$T^{\prime }$ strongly maximizes over T iff

(i) $T^{\prime }$ inconsistently maximizes over T, and

(ii) there is no consistent $T^{\prime \prime }$ extending T that properly maximizes over $T^{\prime }$ . ([14, p. 224])

I won’t attempt to explain each of the components of this definition, but rather direct attention to clause (ii) where we find something very like matching. We are demanding that T cannot be extended to match $T^{\prime }$ . ³¹

We shall defer exposition of the third idea until we are ready for it. Our goal is to now demonstrate that in the context of faithful interpretations the ability for one theory to match one another is all but trivial. In order to set this up, however, we start with a proof of a toy proposition that will provide a template for the main lemmas that follow in this section. In essence, it shows that matching is cheap. However, inspection of at least the toy claim below will also reveal something of how weak the relationship can be between one theory and another that faithfully interprets it. While the conditions on this proposition are somewhat technical, they are also quite easy to satisfy. Moreover, it’s the punchline that is important. ³²

Proposition 14. Suppose: S and T are theories extending $ZFC$ ; for all reals $x\in \mathbb {R}$ , there is an $\omega $ -model $\mathcal {M}$ of S with $x\in \mathcal {M}$ ; S proves that T is consistent; and S is generic invariant under set forcing. Then S faithfully interprets T.

Proof. Our goal is to show there is an interpretation $s:mod(S)\to mod(T)$ which is a surjection up to elementary equivalence. It is convenient to first verify the surjectivity part of the claim. Let $\mathcal {N}$ be a model of T and $x\in \mathbb {R}$ code $\mathcal {N}$ . Then fix an $\omega $ -model $\mathcal {M}$ of S with $x\in \mathcal {M}$ and without loss of generality, suppose $\mathcal {M}$ is countable. We now define s by working in $\mathcal {M}$ . Given that S proves the consistency of T and S extends $ZFC$ , we can perform the completeness proof inside $\mathcal {M}$ . Recall Henkin’s method of extending T to a maximal consistent set of sentences in which every existential sentence is witnessed by a constant symbol. We let the Henkin tree be the result of following this procedure except that when we come to a sentence $\varphi $ where both it and its negation are consistent with what we have added so far, we avoid choosing and rather fork into one branch for $\varphi $ and one for $\neg \varphi $ . Since $\mathcal {M}$ is an $\omega $ -model, it is easy to see that every infinite path through the tree allows us to define a model of T. Moreover, every complete theory extending T occurs as a branch in the tree; thus, up to elementary equivalence every model of T is definable from a branch in this tree. To define a particular branch we use the continuum pattern between, say, $\aleph _{0}$ and $\aleph _{\omega }$ . Call this $s(\mathcal {M})$ . Note that there is no reason to think $s(\mathcal {M})\equiv \mathcal {N}$ ; however, since $x\in \mathcal {M}$ we may define a forcing in $\mathcal {M}$ that modifies the continuum pattern such that a branch defining $\mathcal {N}$ is determined. And since $\mathcal {M}$ is countable, we may let $\mathcal {M}[G]$ be the corresponding generic extension which is still a model of T. Then $s(\mathcal {M}[G])\equiv \mathcal {N}$ as required. This verifies that s is a surjection that is possibly partial.

To see that s is defined on every model $\mathcal {M}$ of S, note that the definitions involved in the interpretation, s, can be articulated in any model of S. So suppose $\mathcal {M}$ is an arbitrary model of S. By our assumption and the completeness theorem, $\mathcal {M}$ thinks there is a model of T. This means that $\mathcal {M}$ will think that the body of its Henkin tree is nonempty and thus a path through the body of this tree will be selected by $\mathcal {M}$ . This is $t(\mathcal {M})$ . Then it can be seen—regardless of whether $\mathcal {M}$ is an $\omega $ -model or not—that $t(\mathcal {M})$ is a model of T, as required.

The following fact is much sharper and requires a more technical proof. Nonetheless, the underlying idea is much the same. We shall use it to provide our first piece of evidence that the ability to provide faithful interpretation does not tell us much.

Fact 15. (Lindström) Suppose S and T are consistent theories extending $ZFC$ ; for every finite $\Delta \subseteq T$ , S proves $\Delta $ is consistent; and for all $\varphi \in \Sigma _{1}^{0}$ if $\varphi $ then $S\vdash \varphi $ (i.e., S is $\Sigma _{1}^{0}$ -sound). Then S faithfully interprets T. ³³

We then put this straight to work to highlight what might appear to be a surprisingly close relationship between $V=L$ and $MC$ .

Proposition 16. Suppose there is a measurable cardinal. Then $V=L$ can be extended to a consistent theory S which faithfully interprets $MC$ .

Proof. By Fact 15, it suffices to find a consistent theory S extending $V=L$ such that S proves that every finite subset of $MC$ is consistent and S is $\Sigma _{1}^{0}$ sound. Let S be

$$ \begin{align*} V=L\cup\{Con(\Delta)\ |\ \Delta\text{ is a finite subset of }MC\}. \end{align*} $$

Clearly S proves all the finite subsets of $MC$ are consistent, and since consistency is implied by $\Sigma _{1}^{0}$ -soundness, it suffices to show that S is $\Sigma _{1}^{0}$ -sound. For this it suffices to show that S has a transitive model. To see this let $\kappa $ be the least inaccessible cardinal and note that $L_{\kappa }$ is a transitive model of $V=L$ . So to show that $L_{\kappa }$ is a transitive model of S, it suffices to that it is true in $L_{\kappa }$ that every finite subset of $MC$ is consistent. Now letting $\Delta $ be such a set, we see by reflection that there is some $V_{\alpha }$ in which $\Delta $ is satisfied. Thus, $\Delta $ is consistent and by an easy application of Lévy–Shoenfield absoluteness we see that $L_{\kappa }$ also says that $\Delta $ is consistent. Thus $L_{\kappa }$ is a transitive model of S.

This proof is easily generalised to give us the following:

Lemma 17. Suppose that $T\supseteq ZFC$ is true and that T proves that there is a transitive model of $V=L$ . Then $V=L$ can be extended to faithfully interpret T.

The upshot of this is that faithful interpretations are just too easy to obtain. If the story above about matching were to work, then it should not be the case that $V=L$ can be extended to match $MC$ . As such, it could seem prudent at this point to abandon faithful interpretations and move higher up the interpretability hierarchy. This is what we aim to do; however, there still remain some plausible ways to explore the space between faithful interpretation and elementary retraction. Moreover, when we look to the proof of our toy Proposition 14, we see that there is something very arbitrary about the models delivered by the interpretation described. For example, the models will generally be ill-founded.

This motivates our third idea. Rather than using arbitrary models and interpretations, we might demand that interpretations of better quality are employed. For example, it might seem reasonable to not be concerned with what happens in interpretations that provide the wrong version of the natural numbers or are, say, ill-founded. Something like this idea is perhaps present in Steel when he talks about interpretative power being constrained to use interpretations that “preserve meaning” [4]. We also see this when Maddy introduces fair interpretations in response to problematic examples proposed by John Steel and Tony Martin. ³⁴

3.2.1 Transitive interpretations

We now show that if we restrict to transitive and even inner models, much the same problem emerges. On this basis, we push back on our third idea by demonstrating that improving the quality of our interpretations does not make them substantively more difficult to obtain. As such, this idea also seems unhelpful in our pursuit of an analysis of restrictiveness. First we consider a restriction to interpretations that are transitive and so we make the following definition. Given set theorists’ well-justified penchant for transitive models, this seems like a natural starting point. Let $transMod(T)$ be the class of transitive models of T when T is an $\mathcal {L}_{\in }$ -theory.

Definition 18. Suppose S and T are theories in $\mathcal {L}_{\in }$ . Let us say that S transitively interprets T if there is an interpretation $s:\mathcal {L}_{\in }\to \mathcal {L}_{\in }$ whose associated mod-functor ensures that ³⁵

$$ \begin{align*} s“transMod(S)\subseteq transMod(T). \end{align*} $$

If s also ensures that for all $\varphi \in \mathcal {L}_{\in }$ ,

$$ \begin{align*} T\models_{trans}\varphi\ \Leftrightarrow\ S\models_{trans}s(\varphi), \end{align*} $$

we say that S faithfully transitively interprets T via s, where $\models _{trans}$ is the consequence relation for transitive models. ³⁶

The idea here is that a transitive interpretation is an interpretation that—when applied in a transitive model—gives rise to another transitive model. Moreover, it is easily seen that the original model will also be able to ascertain that the defined model is transitive. As in the general case, the faithful transitive interpretations then ensure that the translation does not overshoot and prove too much. We then observe there is a natural strengthening of faithful interpretation that fits well with the proof strategy of Proposition 14.

Proposition 19. Suppose $s:transMod(S)\to transMod(T)$ is a mod-functor which is a surjection up to elementary equivalence. Then T faithfully transitively interprets S. ³⁷

With this in hand, we may now prove a generalisation of Theorem 14 that will give us another example like that of Proposition 16. The key difference is that rather than using the ordinary proof theory of first order logic, we make use of the Lévy–Shoenfield theorem to provide an analogous “proof” tree for the logic of transitive models.

Theorem 20. Suppose: S and T are theories extending $ZFC$ ; for every real $x\in \mathbb {R}$ , there is a transitive model M of S with $x\in M$ ; S proves that T has a transitive model; and S is generic invariant under set forcing. Then S faithfully transitively interprets T.

Proof. We aim to define an interpretation $s:transMod(S)\to transMod(T)$ that is a surjection up to elementary equivalence. We work on surjectivity first. Since S has a transitive model and proves that T has a transitive model, we see by Shoenfield absoluteness that there is a transitive model of T. Fix such a model, N. Let $N^{*}$ be a countable elementary submodel of N and let $x\in \mathbb {R}$ be a code for $N^{*}$ . Then by our assumption, we may fix a transitive model M of S with $x\in M$ , which we assume is countable without any loss of generality.

Working in M, we now define s. Observe that the statement that there is a transitive model of T is $\Sigma _{2}^{1}$ . Thus, there is a Lévy–Shoenfield tree $\mathcal {T}$ consisting of pairs of finite sequences into $\omega $ and $\omega _{1}$ respectively such that for all $y\in \mathbb {R}$ , ³⁸

$$ \begin{align*} y\ \text{codes a transitive model of }T & \Leftrightarrow y\in p[\mathcal{T}]\\ & \Leftrightarrow\exists f:\omega\to\omega_{1}\ \langle y,f\rangle\in[\mathcal{T}]. \end{align*} $$

Now observe that since $x\in M$ and M is transitive, M can correctly verify that x is a code for a model of T. Thus working in M, we see that there is some $g:\omega \to \omega _{1}$ such $\langle x,g\rangle \in [\mathcal {T}]$ . To complete the definition of our interpretation it suffices to define a particular branch through $\mathcal {T}$ since we can obtain a transitive model by taking the first coordinate and collapsing it. To define a path through $\mathcal {T}$ we note that we may select a particular path through $\mathcal {T}$ using a function $h:\omega \to \omega _{1}$ that chooses a path through $\mathcal {T}$ by using the values of h to choose which way to go when $\mathcal {T}$ forks. Such a function can be defined by consulting a definable $\omega _{1}$ -sequence of the continuum pattern in $\mathcal {M}$ . We then let $s(M)$ be the model obtained from the function defined from such a sequence. In general, $s(M)\not \equiv N$ ; however, if we force to change the continuum pattern to obtain $M[G]$ in which the function $h:\omega \to \omega _{1}$ determining N is definable. Then we have $s(M[G])\equiv N$ where $M[G]$ is a model of S, establishing that s is a partial surjection.

Finally, to see that s is defined for all models of T, note that definitions composing s can be articulated in any transitive model M of S. Let M be such a model. Then by our assumption M thinks that there is a transitive model of T and by absoluteness, S is correct about this. Fix such a model $N\in M$ . Then, N thinks that $p[\mathcal {T}]$ is nonempty and thus, the model defined from the continuum pattern in M is a transitive model of T.

We are then able to find a new example where a seemingly restrictive theory is able to match a theory that might otherwise have appeared out of reach.

Proposition 21. Let $S^{*}$ be the theory extending $ZFC$ by saying that there is some real $x\in \mathbb {R}$ such that the universe is a set generic extension of $L[x]$ , abbreviated $V=L[x,G]$ . Then there is some S extending $S^{*}$ that faithfully transitively interprets $MC$ , if some $V_{\alpha }$ is a model of $MC$ .

Proof. Let S be $S^{*}$ extended with the statement that there is a transitive model of $MC$ . Then by Theorem 20, it suffices to show that: (1) for all $x\in \mathbb {R}$ there is a transitive model M of S such that $x\in M$ ; and (2) S is set generic invariant. To see (1), let $y\in \mathbb {R}$ and let $V_{\alpha }$ be a model of $MC$ . Then $L_{\alpha }[y]$ is a model of $ZFC$ plus the statement that for some $x\in \mathbb {R}$ the universe is a (trivial) generic extension of $L[x]$ . Moreover, by the Lévy–Shoenfield theorem we see that $L_{\alpha }[y]$ recognizes that there is a (countable) transitive model of $MC$ . Thus, $L_{\alpha }[y]$ is a model of S. For (2), suppose M is a transitive model of S. Then $M=L_{\alpha }[x,G]$ for some $\alpha \in Ord$ , $x\in \mathbb {R}$ and G is $\mathbb {P}$ -generic over $L_{\alpha }$ for some $\mathbb {P}\in L_{\alpha }$ . It then suffices to show that if H is $\mathbb {Q}$ -generic over M for some $\mathbb {Q}\in M$ , then $M[H]$ is still a model of T. To see this observe that if H is $\mathbb {Q}$ -generic over $L_{\alpha }[x,G]$ , then by the iteration lemma we see that $G*H$ is $\mathbb {P}*\mathbb {\dot {Q}}$ -generic over $L_{\alpha }[x]$ where $\dot {\mathbb {Q}}$ is such that $\dot {\mathbb {Q}}_{G}=\mathbb {Q}$ . ³⁹

To hammer this home, I must argue that we should intuitively think that saying the universe is a generic extension of $L[x]$ for some $x\in \mathbb {R}$ is a restrictive addition to $ZFC$ . The most obviously restrictive aspect is that a model of $V=L[x,G]$ thinks the universe is constructed from two sets. As such, there would seem to be all manner of objects beyond x and G that are ruled out by such a theory. But we can say more. Observe that $MC$ implies that $\mathbb {R}^{\#}$ exists, ⁴⁰ while on the other hand, it can be seen that $V=L[x,G]$ implies that $\mathbb {R}^{\#}$ does not. As such, we are in an analogous situation to the comparison between $V=L$ and $ZFC$ . In that case, we saw both Maddy and Steel remark that $V=L$ was a restrictive theory since it did not allow us to go beyond L and talk about $0^{\#}$ . Similarly here, we see that $V=L[x,G]$ is restrictive since it doesn’t allows us to talk about $\mathbb {R}^{\#}$ .

Thus, it seems that the restriction to transitive models is also unhelpful for the purposes of analyzing restrictiveness. ⁴¹ Nonetheless an inspection of the proof of Theorem 20 reveals that despite being transitive, the models provided are hardly ideal. In particular, the models provided by the underlying completeness theorem are all countable. Thus, while they correctly represent the natural numbers, they do not correctly calculate a single uncountable ordinal.

3.2.2 Inner model interpretations

An obvious response to the small size of the transitive models obtained in the previous section is to demand that our interpretations provide inner models, i.e., transitive classes containing all the ordinals. ⁴² It is not difficult to define a notion of inner model interpretability; however, we shall make use of something stronger and arguably better. The reason for this is the difficulties involved in obtaining proper class models that are also transitive. ⁴³ The problem then is that, in general, M will not think that the internal model is transitive and thus it is not an inner model. Thus, we take a different path.

In essence, our idea is to generalize the proof of Theorem 20 to obtain a countable transitive model that can be—so to speak—stretched out into an inner model. The existence of such models requires some large cardinal strength and takes us into the lower regions of the hierarchy that transcends L. First we define what it means for a model to be stretchable in the right way.

Definition 22. For theories T extending $ZFC$ , let an iterable model of T be a transitive model M such that $M=V_{\kappa }^{M^{*}}$ for some transitive model $M^{*}$ of $ZF\backslash \{\mathcal {P}\}$ and $\kappa \in M^{*}$ where that there is an $M^{*}$ -ultrafilter U on $\kappa $ such that $M^{*}$ is iterable by U.

We then see that such models can be stretched out in the manner required for our application.

Fact 23. If M is an iterable model of T, then there is an inner model of T.

Proof. We show that there is a definable model with the same complete theory as M. Let M be an iterable model as witnessed by $M^{*}$ , $\kappa \in M^{*}$ and U. Then by assumption, $Ult_{\alpha }(M^{*},U)$ is transitive for all $\alpha \in Ord$ . Moreover,

$$ \begin{align*} \langle\langle Ult_{\alpha}(M^{*},U)\rangle_{\alpha\in Ord},\langle i_{\alpha,\beta}\rangle_{\alpha\leq\beta\in Ord}\rangle \end{align*} $$

forms a directed system. Let $M_{Ord}^{*}$ be the direct limit of this system and we have then defined an internal model in which the image $i_{Ord}(\kappa )$ of $\kappa $ is isomorphic to the ordinals. This means that transitive collapse $M_{Ord}$ of $M_{Ord}^{*}$ is only defined up to $Ord$ , an initial segment of $M_{Ord}^{*}$ , and this entails that

$$ \begin{align*} M_{Ord}=trcoll(M_{Ord}^{*})\cong(V_{i_{Ord}(\kappa)})^{M_{Ord}^{*}}\equiv(V_{\kappa})^{M^{*}}=M.\\[-32pt] \end{align*} $$

Thus, we see that being an iterable model is a stronger property than being an inner model in that, in general, there will be inner models of some theory extending $ZFC$ that are not elementary equivalent to any iterable model of that theory. I think the right way to look at this is to think that iterable models are actually of superior quality than inner models. To put it a little odd, if we were able to look at the universe of sets—so to speak—from the outside, then we’d expect the universe to be iterable in much the same way we’d expect it to be transitive. ⁴⁴ We may then define a notion of iterable interpretability as follows. First let $itMod(T)$ be the class of iterable models of T for some T extending $ZFC$ .

Definition 24. For theories $T,S\supseteq ZF$ , we say that S iterably interprets T if there is an interpretation $s:\mathcal {L}_{\in }\to \mathcal {L}_{\in }$ such that

$$ \begin{align*} s“itMod(S)\subseteq itMod(T). \end{align*} $$

We say S faithfully iterably interprets T if S iterably interprets T via s and for all $\varphi \in \mathcal {L}_{\in }$

$$ \begin{align*} T\models_{it}\varphi\ \Leftrightarrow\ S\models_{it}s(\varphi), \end{align*} $$

where $\models _{it}$ is the consequence relation restricted to iterable models.

The idea here is the natural generalization of Definition 18 to iterable models. We then obtain a similar result:

Theorem 25. Suppose: S and T are theories extending $ZFC$ ; for every $x\in \mathbb {R}$ , there is an iterable model M of S with $x\in M$ ; S proves that there is an iterable model of T and that for all $x\in \mathbb {R}$ , $x^{\#}$ exists; ⁴⁵ and S is generic invariant under sufficiently closed set forcing. ⁴⁶ Then S faithfully iterably interprets T.

The main change here from the proof of Theorem 20 is that we replace the first order “proof theory” with the Martin–Solovay tree rather than the Lévy–Shoenfield tree and we assume sufficiently many large cardinals exist to ensure the construction works.

Proof. We aim to define an interpretation $s:itMod(S)\to itMod(T)$ that is a surjection up to elementary equivalence. First we note that T has an iterable model. This is because S proves that T has an iterable model and iterable models are correctly calculate whether models they contain are iterable. Fix such a model, N. We want our interpretation s to ensure that $N\equiv s(M^{\dagger })$ for some iterable model $M^{\dagger }$ of S. Let $N^{*}$ be a countable elementary submodel of N and let $x\in \mathbb {R}$ be a code for $N^{*}$ . Note that by a copy and paste argument, it can be seen that $N^{*}$ remains iterable. ⁴⁷ Then, by our assumption, we may fix an iterable model M of S with $x\in M$ .

Working in M, we now define s. First observe that the statement that there is an iterable model of T is $\Sigma _{3}^{1}$ . Let $\tilde {L}=\bigcup _{x\in \mathbb {R}}L[x]$ as defined in M and now work in $\tilde {L}$ . Then using our assumption that every real has a sharp we may define a Martin–Solovay tree $\mathcal {T}$ consisting of pairs of finite sequences from $\omega $ and $\gamma $ such that for all $y\in \mathbb {R}$ ,

$$ \begin{align*} y\text{ codes an iterable model of }T & \Leftrightarrow y\in p[\mathcal{T}]\\ & \Leftrightarrow\exists f:\omega\to\gamma\ \langle y,f\rangle\in[\mathcal{T}], \end{align*} $$

where $\gamma $ is the supremum of the ordinals occurring in $\mathcal {T}$ . ⁴⁸ Note that since $x\in M$ and M is iterable, M can correctly verify that x is a code for an iterable model of T. This verification is also correctly executed in $\tilde {L}^{M}$ . Thus there is some $g:\omega \to \gamma $ in $\tilde {L}^{M}$ such that $\langle x,g\rangle \in [\mathcal {T}]$ . To complete our definition of s, it suffices to define a particular branch through $\mathcal {T}$ . From such a branch, we can then extract a code and then collapse it into an iterable model. We then note that a function $h:\omega \to \gamma $ can be used to pick a path through $\mathcal {T}$ by letting it decide what to do at points where the tree forks. Such a function can be defined by consulting a definable $\gamma $ sequence of the continuum pattern commencing at the greater of $\gamma ^{+}$ and $\lambda $ , where $\lambda $ is the least ordinal such that M thinks that all $\lambda $ -closed posets force S. We let the resultant model be $s(M)$ of T. Of course, there is no reason to think that $s(M)\equiv N$ ; however, since M is invariant under $\lambda $ -closed set forcing, we may force to change the continuum pattern giving $M[G]$ where the function $h:\omega \to \gamma $ that yields $\langle x,g\rangle $ and thus N. Then since the obvious forcing is $\gamma ^{+}$ closed we see that $[\mathcal {T}]=[\mathcal {T}]^{M[G]}$ and so $t(M[G])\equiv N$ . This establishes that s is a (possibly) partial surjection up to elementary equivalence.

Finally, to show that s is defined for all models of S, let M be an arbitrary iterable model of S. By our assumption, we see that M believes that there is an iterable model N of T. Thus M thinks that its version of $p[\mathcal {T}]$ is non empty and so the model $t(M)$ defined from the continuum pattern in M is such that M thinks it is iterable. And since M itself is iterable it is correct in its calculation of this $\Pi _{2}^{1}$ fact about $t(M)$ .

Once again, we are able to obtain an example where an apparently restrictive theory is able to match a theory that could appear beyond its range. ⁴⁹

Proposition 26. Let $S^{*}$ be the theory $ZFC$ plus the statement: $\exists x\in \mathbb {R}\exists U,\kappa $ such that U is a normal ultrafilter on $\kappa $ and V is a $\kappa ^{+}$ -closed generic extension of $L[U,x]$ , abbreviated $V=L[U,x,G]$ . Then $S^{*}$ can be extended to some S that faithfully iterably interprets $ZFC$ plus there is an extendible cardinal, abbreviated $Ext$ , if some $V_{\alpha }$ satisfies $Ext$ .

Proof. Let S be $S^{*}$ plus the statement that there is an iterable model of $Ext$ . By Theorem 25, it suffices to show that: (1) for all $x\in \mathbb {R}$ , there is an iterable model M of S with $x\in M$ ; (2) S proves that for all $x\in \mathbb {R}$ , $x^{\#}$ exists; and (3) S is invariant under set generic forcing.

For (1), let $y\in \mathbb {R}$ , $V_{\alpha }$ satisfy $Ext$ , $\kappa <\alpha $ be the least measurable cardinal and U be a normal ultrafilter on $\kappa $ . Then $L_{\kappa }[U,y]$ is a model of $ZFC$ plus the statement that the universe is a (trivial) generic extension of $L[x,U]$ for some $x\in \mathbb {R}$ and L-normal ultrafilter U by a poset which is vacuously $\kappa ^{+}$ -closed. For (2) we note that S entails that there is a measurable cardinal and thus that every real $x\in \mathbb {R}$ has a sharp. Finally for (3), we note that the finite iteration of $\kappa ^{+}$ -closed forcings give $\kappa ^{+}$ -closed forcings. Moreover, the result of such forcing ensures that $\kappa $ remains measurable and the universe. ⁵⁰

To bring home the point of this example, I need to argue the theory, $V=L[U,x,G]$ , should intuitively be regarded as restrictive. As above, there is a sense in which we just can see the restrictiveness of this theory in that a model of $V=L[U,x,G]$ says that the universe has been constructed from a mere three sets. Beyond this we also observe that $Ext$ very easily implies that there is more than one measurable cardinal. On the other hand, $V=L[U,x,G]$ implies there is only one measurable cardinal. Thus, $V=L[U,x,G]$ does not allow us to talk about normal ultrafilters on multiple cardinals and so fits our template for identifying intuitive examples of restrictiveness. Thus, even if we restrict our attention to models that are of a very good quality, faithful interpretation is just too cheap.

In this section, we investigated some of the upper reaches of what lies beneath elementary retraction. We’ve argued that for the purposes of analyzing the relative restrictiveness of theories, faithful interpretation—however strengthened—is too easy to obtain to be of any significance. Even if we allow that our interpretations are iterable, reasonable assumptions about background large cardinals ensure that what very plausibly appear to be restrictive theories are able to match anything you can throw at them. We are now ready to return to elementary-retraction.

4 Forcing forcing into the picture

Having seen the difficulties involved with strong faithful interpretations and the attempt to track isomorphisms, the results of Section 2.1 indicate that we should be taking elementary retraction as a serious candidate for our analysis of restrictiveness. We shall soon see that this path is also fraught but by a different difficulty. To see this, let us first put forward the obvious definition:

Definition 27. T is elementary restrictive with respect to S if:

• • T is an elementary retract of S; but

• • S is not an elementary retract of T.

Recalling our canonical example, we are looking for an analysis that confirms that $V=L$ is restrictive with respect to $ZFC$ . Back at Theorem 4, we learned that $V=L$ is a retract of $V=L[c]$ , from which it is easily seen that it is also an elementary-retract of $ZFC$ . We also saw that—in the other direction— $V=L$ is not a retract of $ZFC$ and thus, by our provisional analysis, we were able to say that $V=L$ was restrictive with respect to $ZFC$ . Perhaps disappointingly, we then saw that this analysis could not account for the closeness of theories related by generic extension, which provided our impetus toward elementary-retractions. Given this, it seems reasonable to put forward the following conjecture.

Conjecture 28. $ZFC$ is not an elementary-retract of $V=L$ .

As far as I know, this question is open. Indeed, I don’t think either of failures of identity-retraction from Proposition 6 have been shown to fail for elementary-retractions. To the best of my knowledge there are only two proofs of a failure of elementary retraction in the literature. The first occurs in [3], where it is shown that a weak version of $ZF_{fin}$ is not an elementary retract of $PA$ . ⁵¹ The second occurs in [25], where it is shown that Robinson arithmetic, Q, is not an elementary retract of any sequential theory. ⁵² My present level of understanding suggests that neither of these proofs can be generalized to deal with the conjecture above. The following seems like the obvious problem in this area to begin work upon:

Problem 29. Is $ZFC\backslash \{Inf\}$ an elementary-retract of $ZFC_{fin}$ ? ⁵³

If things were working according to plan, the answer would be negative. To stack the deck a little suppose there was some very large cardinal $\kappa $ and some worldly cardinal $\lambda $ above it such that $V_{\lambda }$ still recognizes that $\kappa $ has this large cardinal property. Then $V_{\lambda }$ is a model of $ZFC\backslash \{Inf\}$ but it seems so very unlikely that there are interpretations that would allow us to define a model of $ZF_{fin}$ in $V_{\lambda }$ from which a model elementary equivalent to $V_{\lambda }$ could then be recovered. That said, some of the results of Section 3 also have a surprising feel and the ground here has barely been turned.

With this—rather human—limitation in mind, we shall now offer a different approach that, more or less, builds generic extension into the story. This kind of response has certain limitations in that, by its definition, it will be taking for granted that the two ways of transforming models of set theory are via inner models and forcing. While this is an adequate representation of actual practice there are no mathematical results that show this assumption is correct and it is difficult to know what might lie around the corner. ⁵⁴ Nonetheless and perhaps in accord with these remarks, there is something a little odd about elementary retraction from a set theoretic point of view. Obtaining identity up to elementary equivalence is equivalent to obtaining a model with the same complete theory as the one we started with. Indeed it is not difficult to see that we may reformulate elementary retraction as follows:

Proposition 30. T is an elementary retract of S if there are interpretations $t,s$ witnessing the mutual interpretability of T and S which are such that for all complete theories $\Gamma $ extending T

$$ \begin{align*} s^{\dagger}\circ t^{\dagger}(\Gamma)=\Gamma, \end{align*} $$

where $t^{\dagger }(\Gamma )=\{\varphi \ |\ t(\varphi )\in \Gamma \}$ and $s^{\dagger }$ is defined similarly.

In this setting, we see that elementary retraction can be construed as an identity retraction in the category of complete theories. ⁵⁵ This is quite pleasing; however, we also see that the techniques of manipulating complete theories are more native to model theory than set theory. As such, the use of elementary retractions could take us too far afield from the techniques used by set theorists to compare theories extending $ZFC$ . Thus, regardless of the outcome for Problem 29, we would still face a choice between: sentential equivalence, which is a purely interpretative relation; and what we call generic equivalence, which leans more heavily on set theoretic techniques.

4.1 Generic retraction

We are now ready to put forward the ultimate analysis of this paper. In essence, we are going to build generic extensions into the machinery of relative interpretation by brute force. However, before I get to far into the exposition, I’d like to stress that I think this proposal should be thought of as a kind of prototype in this project. As we shall see, there will still be limitations and idiosyncrasies on the road ahead. As such, I think future workers in this area should feel free to dismantle and rebuild, much in the same way I have done with Maddy and Steel’s work above.

The main problem for dealing with generic extensions using interpretability is that the outputs of mod-functors have domains that are subsets of their input domains: they yield internal models. Forcing, on the other hand, does not give internal models. This is a well-known problem that many would regard as open. But the reason for this is not that no plausible solution can be offered, but rather that there are too many solutions on the table with little clear choice between them. With this in mind, we aim to offer a simple approach that—while somewhat limited—aims to retain the pleasing model theoretic intuitions afforded by inner models, by treating generic extensions as genuine outer models. Moreover, we shall also demand that the models used are transitive and thus of good quality by the lights of the set theoretic community.

Informally, a generic interpretation will take a countable transitive model M and some M-generic G and then define an inner model of $M[G]$ that will be the output model. In a nutshell, we first move out and then back in. Ideas similar to this have some precedent in Steel:

The way we interpret set theories today is to think of them as theories of inner models of generic extensions of models satisfying some large cardinal hypothesis, and this method has had amazing success. We do not seem to lose any meaning this way. It is natural then to build on this approach. [22, p. 165] ⁵⁶

To implement this, we now define generic interpretation.

Definition 31. A generic interpretation $i:\mathcal {L}_{\in }\to \mathcal {L}_{\in }$ is given by a pair $\langle \mathbb {P}_{i},t_{i}\rangle $ where $\mathbb {P}_{i}$ is a term for a definable poset ⁵⁷ and $t_{i}$ is an interpretation from $\mathcal {L}_{\in }$ to $\mathcal {L}_{\in }$ expanded by the $\mathbb {P}_{i}$ -names $\check {V}$ and $\dot {G}$ ⁵⁸ which is such that for all $\varphi \in \mathcal {L}_{\in }$ ,

$$ \begin{align*} i(\varphi)=\ \Vdash_{\mathbb{P}_{i}}t_{i}(\varphi) \end{align*} $$

such that $\mathbb {P}_{i}$ forces ⁵⁹ that $t_{i}$ defines a transitive model; i.e.,

$$ \begin{align*} \Vdash_{\mathbb{P}_{i}}\{x\ |\ \delta_{t_{i}}(x)\}\text{ is transitive.} \end{align*} $$

With this in hand, we can then define what it means when one theory generically interprets another. First a little notation: for a theory T in $\mathcal {L}_{\in }$ , let $ctm(T)$ be the set of countable transitive models of T. Let $\models _{ctm}$ be the consequence relation for countable transitive models; thus, we write $T\models _{ctm}\varphi $ to mean that for all $M\in ctm(T)$ , $M\models \varphi $ .

Definition 32. Let T and S be theories extending $ZFC$ . We say T generically interprets S if there is a generic translation such that for all $\varphi \in \mathcal {L}_{\in },$ ⁶⁰

$$ \begin{align*} S\models_{ctm}\varphi\ \Rightarrow\ T\models_{ctm}i(\varphi). \end{align*} $$

Informally, the idea is that we force outward using $\mathbb {P}_{i}$ and then use $t_{i}$ to define a transitive internal model within the generic extension. We now make this formal by defining a generic counterpart to the mod-functor for ordinary interpretations. For M a countable transitive model and $\mathbb {P}$ a poset in M, let $gen(M,\mathbb {P})$ be the set of M-generic filters of $\mathbb {P}$ . Now suppose that T generically interprets S via i which is determined by $\langle \mathbb {P}_{i},t_{i}\rangle $ . We may then define a gen-functor that takes a countable transitive model M of T and an M-generic G over $\mathbb {P}_{i}$ and then applies $t_{i}$ to $M[G]$ to obtain $i^{*}(\langle M,G\rangle )$ . More formally, $i^{*}:\sum _{M\in ctm(T)}gen(M,\mathbb {P}_{i})\to ctm(S)$ is such that for all $M\in ctm(T)$ and M-generic G over $\mathbb {P}_{i}$ ,

$$ \begin{align*} i^{*}(\langle M,G\rangle)=t_{i}(M[G]). \end{align*} $$

The key difference from an ordinary interpretation is the inclusion of the generic parameter. As with ordinary interpretations, we shall abuse notation and write i instead of $i^{*}$ . We now verify that the existence of a generic functor is indeed equivalent to there being a generic interpretation.

Lemma 33. Let T and S be theories extending $ZFC$ . Then following are equivalent where i is determined by $\langle \mathbb {P}_{i},t_{i}\rangle $ :

1. (1) T generically interprets S via i; and

2. (2) $i:\Sigma _{M\in ctm(T)}gen(M,\mathbb {P}_{i})\to ctm(S)$ .

Proof. (1 $\to $ 2) Suppose M is a countable transitive model of T and G is $\mathbb {P}_{i}$ -generic over M. By (1), we see that for all $\varphi \in \mathcal {L}_{\in }$ ,

$$ \begin{align*} M\models i(\varphi) & \Leftrightarrow M\models“\Vdash_{\mathbb{P}_{i}}t_{i}(\varphi)”\\ & \Rightarrow M[G]\models t_{i}(\varphi)\\ & \Leftrightarrow t_{i}(M[G])\models\varphi\ \Leftrightarrow\ i(\langle M,G\rangle)\models\varphi. \end{align*} $$

Then since by (1) $M\models i(\varphi )$ for all $\varphi \in S$ , we see $i(\langle M,G\rangle )\models S$ as required.

(2 $\to $ 1) Suppose $T\not \models _{ctm}i(\varphi )$ and fix a countable transitive model M of T such that $M\models \neg i(\varphi )$ . Thus, working in M we see that $\nVdash _{\mathbb {P}_{i}}t_{i}(\varphi )$ and so we may fix some $p\in \mathbb {P}_{i}$ such that $p\Vdash _{\mathbb {P}_{i}}t_{i}(\neg \varphi )$ . Now let G be $\mathbb {P}_{i}$ -generic over M and such that $p\in \mathbb {P}_{i}$ . Then $M[G]\models t_{i}(\neg \varphi )$ and so $t_{i}(M[G])\models \neg \varphi $ and by (2) $t_{i}(M[G])\models S$ . Thus, $S\not \models _{ctm}\varphi $ .

This sets us up well, but we should still verify that generic interpretation is transitive; i.e., if T generically interprets S and S generically interprets U, then we want it to be the case that T generically interprets U. By the previous lemma if suffices to show that:

Lemma 34. Suppose that for theories $T_{0},T_{1}$ and $T_{2}$ extending $ZFC$ there are gen-functors such that

$$ \begin{align*} i_{0}:\prod_{M\in ctm(T_{0})}gen(M,\mathbb{P}_{0})\to ctm(T_{1})\text{ and }i_{1}:\prod_{M\in ctm(T_{1})}gen(M,\mathbb{P}_{1})\to ctm(T_{2}). \end{align*} $$

Then there exists a gen-functor $j:\prod _{M\in ctm(T_{0})}gen(M,\mathbb {P}_{j})\to ctm(T_{2}).$

Proof. Let M be a countable transitive model of T. Then let $G_{0}$ be $\mathbb {P}_{0}$ -generic over M and $G_{1}$ be $\mathbb {P}_{1}$ -generic over $M[G_{0}]$ . ⁶¹ Then by our assumptions we see that

$$ \begin{align*} t_{0}(M[G_{0}]\models T_{1}\ \text{and}\ t_{1}(t_{0}(M[G_{0}])[G_{1}])\models T_{2}. \end{align*} $$

We now define j. First we observe that M can define $\mathbb {P}_{0}$ -name, $\dot {\mathbb {P}}_{1}$ , such that whenever H is $\mathbb {P}_{0}$ -generic over M and $x\in t_{0}(M[H])$ ,

$$ \begin{align*} x\in(\dot{\mathbb{P}}_{1})_{H}\ \Leftrightarrow\ t_{0}(M[H])\models x\in\mathbb{P}_{1}. \end{align*} $$

Thus, M may define $\mathbb {P}_{j}=\mathbb {P}_{0}*\dot {\mathbb {P}}_{1}$ and this will be the poset of our interpretation. We then seen that $G_{0}*G_{1}$ is an arbitrary $\mathbb {P}_{0}*\dot {\mathbb {P}}_{1}$ -generic over M. It will then suffice to show that there is an interpretation $t_{j}$ that allows us to define

$$ \begin{align*} t_{1}(t_{0}(M[G_{0}])[G_{1}]) \end{align*} $$

in $M[G_{0}*G_{1}]$ in a uniform manner using only M and $G_{0}*G_{1}$ as parameters. Recall that we have access to M and $G_{0}*G_{1}$ since $t_{j}$ will be a translation into $\mathcal {L}_{0}(\check {V},\dot {G}).$ We then note that $G_{0}$ and $G_{1}$ can be defined from $G_{0}*G_{1}$ . Thus we see that $M[G_{0}]$ and $t_{0}(M[G_{0}])$ can be defined from M and $G_{0}$ . And then $t_{0}(M[G_{0}])[G_{1}]$ and $t_{1}(t_{0}(M[G_{0}])[G_{1}])$ can be defined from $t_{0}(M[G_{0}])$ and $G_{1}$ , as required.

Thus, we see that generic interpretability is a transitive relation. ⁶² Finally, we are in a position to define the core notion for our analysis of restriction: generic retraction.

Definition 35. For theories T and S extending $ZFC$ , let us say that T is a generic retraction of S if T and S are mutually generically interpretable as witnessed by generic interpretations i and j; i.e.,

$$ \begin{align*} i:\Sigma_{M\in ctm(T)}gen(M,\mathbb{P}_{i})\to ctm(S)\ \text{and}\ j:\Sigma_{M\in ctm(S)}gen(M,\mathbb{P}_{j})\to ctm(T), \end{align*} $$

and for all $M\in ctm(T)$ there exists a $\mathbb {P}_{i}$ -generic $G_{i}$ over M and a $\mathbb {P}_{j}$ -generic $G_{j}$ over $t_{i}(M[G_{i}])$ such that

$$ \begin{align*} M=t_{j}(t_{i}(M[G_{i}])[G_{j}]). \end{align*} $$

We say that T and S are generically equivalent if i and j witness that they are generic retractions of each other.

Informally, the idea here is that we start from a model M of T and then generically extend and take an inner model of S using i; and then we use j to take a generic extension and obtain an inner model of T which ends up being identical to M. Here is an example of generic retraction. Recall that these theories are sententially equivalent and so $V=L[c]$ is an elementary retraction of $V=L$ .

Proposition 36. $V=L[c]$ is a generic retraction of $V=L$ .

Proof. Let $i:\Sigma _{M\in ctm(V=L[c])}gen(M,\mathbb {P}_{i})\to ctm(V=L)$ be determined from a trivial $\mathbb {P}_{i}$ and $t_{i}$ which relativizes all quantifiers to L. Let $j:\Sigma _{M\in ctm(V=L)}gen(M,\mathbb {P}_{j})\to ctm(V=L[c])$ be determined by letting $\mathbb {P}_{j}$ be $\langle 2^{<\omega },\supseteq \rangle $ and $t_{i}$ be trivial. Then if we take a countable transitive model M of $V=L[c]$ , we see that $M=L_{\alpha }[G]$ for some $\alpha <\omega _{1}$ and Cohen real G. We then see that $i(\langle M,H\rangle )=L_{\alpha }$ where H is some trivial $L_{\alpha }$ -generic. Now we observe that G is $\mathbb {P}_{j}$ generic over $i(\langle M,H\rangle )$ and so

$$ \begin{align*} j(\langle i(\langle M,H\rangle),G)=L_{\alpha}[G]=M.\\[-32pt] \end{align*} $$

This is what we expected; however, we can also do something with generic retraction that we could not with sentential retraction by showing an example where it fails. Let $V=L(\mathbb {R})$ be $ZFC$ extended by the statement that the universe is constructed from the reals.

Proposition 37. $V=L(\mathbb {R})$ is a generic retraction of $ZFC$ but $ZFC$ is not a generic retraction of $V=L(\mathbb {R})$ , if there is a transitive model of $ZFC$ that thinks it has a proper class of measurable cardinals.

Proof. To see that $V=L(\mathbb {R})$ is a generic retraction of $ZFC$ , we just observe that $V=L(\mathbb {R})$ is an identity retraction of $ZFC$ . To see that $ZFC$ is not a generic retract of $V=L(\mathbb {R})$ , suppose toward a contradiction that it is and fix generic interpretations witnessing this. Let M be a countable transitive model that thinks it has a proper class of measurable cardinals. Then for any $\mathbb {P}_{j}$ -generic $G_{j}$ over M we see that $N=t_{j}(M[G_{j}])$ is a model of $V=L(\mathbb {R})$ , so we may assume without loss of generality that $t_{j}$ restricts quantification to $L(X)$ for some $X\subseteq \mathbb {R}$ that is definable in $M[G_{j}]$ ; thus we have $N=L(X)^{M[G_{j}]}$ . Since M thinks it contains a proper class of measurable cardinals, so does $M[G_{j}]$ . Let $\kappa $ be the least of these and fix $U\in M$ such that M thinks U is a normal ultrafilter on $\kappa $ .

It will suffice to show that $U\notin N[H]$ for any N-generic H, since then we have $U\in M$ but $U\notin N[G_{i}]\supseteq t_{i}(t_{j}(M[G_{j}])[G_{i}])$ . To see this suppose not and fix H that witnesses this. We then see that

$$ \begin{align*} U^{*}=\{Z\subseteq\mathcal{P}(\kappa)\cap N\ |\ \exists Y\in U\ Y\subseteq Z\}\in N[H] \end{align*} $$

is a normal $N[H]$ -ultrafilter. Thus, $N[H]$ thinks $X^{\#}$ exists. But this is impossible since X forms the reals of N and N is a model of $V=L(\mathbb {R})$ .

These results give us a basic theory of generic interpretation and demonstrate some alignment with our intuitions on these matters. This prompts the penultimate analysis of restrictiveness for this paper.

Definition 38. We then say that T is generically restrictive with respect to S if:

• • T is a generic retraction of S; and

• • S is a not generic retraction of T.

Informally speaking, this tells us that while S can deposit its models with T and get exactly the same model back, there is no uniform means for S to do the same for T: at least one of the models will come back different.

4.2 Comparing theories that are not mutually interpretable

Up until now we’ve restricted our analysis of restrictiveness to comparisons between theories that are—in some sense—mutually interpretable. This has allowed us to focus our attention on what I believe is the core problem, but it has come at a cost. Among other things, it means that we are unable to directly address the canonical example comparing $V=L$ with $MC$ . Fortunately, it’s relatively straightforward to address this.

Definition 39. Let us say that S is generally restrictive if S generically interprets T, but T cannot be extended to some $T^{*}\supseteq T$ such that S is a generic retraction of $T^{*}$ .

The reader will observe that this is a kind of matching condition, which we know from Section 3.2 is unhelpful for various versions of faithful interpretation. However, the increased uniformity in the definition of retraction makes the method feasible. We also see by Proposition 5(2) that in situations where T and S are mutually generically interpretable, general restrictiveness essentially reduces to generic restrictiveness. ⁶³

To see how this works, let’s consider a couple of examples. First we consider a case where we don’t expect restrictiveness. Consider the theories $MC$ and $EXT$ . We see that $EXT$ can interpret $MC$ but $MC$ cannot generically interpret $EXT$ . However, we don’t think that $EXT$ is restrictive in comparison with $MC$ . And according to the definition offered here it is not, since $EXT$ is an extension of $MC$ and $EXT$ is clearly a generic retraction of itself. So far so good. Now let us return to the canonical example: a case where we expect restrictiveness. The following proposition suffices to verify that $V=L$ is generically restrictive with respect to $MC$ .

Proposition 40. $V=L$ cannot be extended to some $T^{*}$ such that $MC$ is a generic retraction of $T^{*}$ .

Proof. Suppose not and fix $T^{*}\supseteq V=L$ along with

$$ \begin{align*} i:\Sigma_{M\in ctm(T^{*})}gen(M,\mathbb{P}_{i})\to ctm(MC)\ \text{and}\ j:\Sigma_{M\in ctm(MC)}gen(M,\mathbb{P}_{j})\to ctm(T^{*}) \end{align*} $$

witnessing this. It suffices to show that i and j cannot even witness mutual generic interpretability. To see this fix a countable transitive $M_{0}$ model of $T^{*}$ and let $N_{0}=j(\langle M_{0},G_{0}\rangle )$ where $G_{0}$ is $\mathbb {P}_{j}$ -generic over $M_{0}$ . We then note that since $N_{0}$ thinks that $0^{\#}$ exists but $M_{0}$ does not, $M_{0}$ can see that $N_{0}$ is wrong about what it thinks is $0^{\#}$ . This entails that $Ord^{N_{0}}<\omega _{1}^{M}<Ord^{M_{0}}$ for otherwise $N_{0}$ would make this calculation correctly. Let $M_{1}=i(\langle N_{0},H_{0}\rangle )$ where $H_{0}$ is $N_{0}$ -generic for its version of $\mathbb {P}_{i}$ . Then clearly $Ord^{M_{1}}\leq Ord^{N_{0}}<Ord^{M_{0}}$ . Repeating the back and forth process infinitely then yields an infinite descending sequence

$$ \begin{align*} Ord^{M_{0}}>Ord^{M_{1}}>\cdots \end{align*} $$

of ordinals, which is impossible.

So as expected $V=L$ is generally restrictive with respect to $MC$ . That’s our analysis of restrictiveness. We have a formal account of restrictiveness based on a generalization of relative interpretability that is able to accommodate forcing. Moreover once understood, the intuitive story about retraction generally makes it quite easy to assess the relative restrictiveness of theory by mere inspection. I take it that this is indicative that we are providing an analysis of a very natural mathematical relation between theories.

However, perhaps the reader is disappointed that after all this work we’ve only considered the canonical example as positive example of general restrictiveness between theories that are not mutually generically interpretable. Fortunately, the technique of the proof above generalizes very widely. Informally speaking, Proposition 40 observes that two theories cannot mutually interpret each other with transitive unless the respective interpretations both give models with the same ordinals. Otherwise we’d end up with an infinite descending chain of ordinals. We close the section by considering a positive case of general restrictiveness emerging from Section 3.2. There we considered cases where various generalizations of faithful interpretability failed to capture cases of prima facie restrictiveness. General restrictiveness addresses these cases easily. We concentrate on the strongest example of this from Section 3.2. Recall that in Proposition 25, we compared the theory $EXT$ with $V=L[U,x,G]$ , which states that the universe is a set generic extension of $L[U,x]$ where U is a normal ultrafilter and $x\in \mathbb {R}$ . We observed that $V=L[U,x,G]$ would naturally be regarded as restrictive since it implies that $U^{\#}$ does not exist. Nonetheless, we were able to show that this theory could be extended to match $EXT$ by providing it with an inner model interpretation. ⁶⁴ We considered this to be a failure of the matching analysis. In contrast we can see that $V=L[U,x,G]$ is in fact generally restrictive with respect to $EXT$ .

Proposition 41. $V=L[U,x,G]$ is generally restrictive with respect to $EXT$ supposing that there is a transitive model of $V=L[U,x,G]$ .

Proof. Clearly $EXT$ generically interprets $V=L[U,x,G]$ , but not conversely. Thus, it will suffice to show that no $T^{*}\supseteq V=L[U,x,G]$ generically interprets $EXT$ . Suppose toward a contradiction that there is some generic interpretation $i:\Sigma _{M\in ctm(T^{*})}gen(M,\mathbb {P}_{i})\to ctm(EXT)$ . Let $M=L_{\alpha }[W,y,H]$ for $\alpha $ least such that $L_{\alpha }[W,y,H]\models \varphi $ where W is a normal ultrafilter according to $L_{\alpha }[W,y,H]$ , $y\in \mathbb {R}$ and H is $L_{\alpha }[W,y,H]$ -generic. Our trailing assumption in the statement of the proposition ensures that a structure exists. Now let J be $(\mathbb {P}_{i})^{M}$ -generic over M. Then $i(\langle M,J\rangle )\models EXT$ . But this is impossible: there is no way of forcing and taking an inner model from M to obtain a model with an extendible cardinal. ⁶⁵

4.3 Some limitations

In this final section, we consider a couple of applications of the analysis above that highlight some limitations of the approach while also giving us a clearer picture of the way theories are connected by generic retraction. Our first example takes us out of the controlled laboratory conditions above and explores a classic equiconsistency proof that exploits forcing while providing very natural interpretations between the theories in question. As such, we might be tempted to think such theories are not restrictive with respect to each other. We shall see that this is not the case on our analysis and then argue that this is the result we should expect. Our second example considers a more bizarre instance of restrictiveness between theories which does not line up with the informal idea of restrictiveness employed with regard to set theory. We then provide a simple means of patching the problem and discuss some implications of this move for the project as a whole.

Example 1

Our first example is a classic equiconsistency that compares two theories and makes essential use of forcing to do so. The interpretations used deploy generic extension and inner models and are good candidates for being meaning preserving in the sense that Steel employs [5, 22]. Let $Inacc$ denote the theory $ZFC$ plus the statement that an inaccessible cardinal exists. Let $ZF+DC+PSP$ be the theory $ZF$ plus dependent choice and the statement that every set of reals has the perfect set property; i.e., every set of reals A is either countable or contains a perfect subset. In other words, every uncountable set of reals contains a nonempty closed set with no isolated points. We then recall the following theorem:

Theorem 42. (Specker) (1) $ZF+DC+PSP$ interprets the $Inacc$ via the translation .

(2) (Solovay) $Inacc$ interprets $ZF+DC+PSP$ via the generic translation determined by collapsing the least inaccessible and then going to its version of $L(\mathbb {R})$ . ⁶⁶

This is a comparatively simple equiconsistency result. So how does our analysis of restrictiveness stand up here? The interpretations used above seem very natural in that they preserve features like the natural numbers and ordinals. As such, one might be tempted to think of these theories as, in some sense, equivalent. Indeed, I think something like this is a common intuition among some set theorists. However despite this, under the interpretations described above, it’s quite clear that neither theory will be a generic retraction of the other. In essence, this is because both interpretations rely on clearly restrictive inner model interpretations: L and $L(\mathbb {R})$ . As such, it is possible with sufficient large cardinal strength to have a model of either theory that—so to speak—contains something too big to be crammed into the inner model in question. Thus, according to our analysis these theories are generically restrictive with respect to each other! This could seem disappointing; however, I think in this case such an attitude is mistaken. Our analysis of restrictiveness is simply more fine-grained that the intuition that $ZF+DC+PSP$ and $Inacc$ are, in some sense, equivalent. There will be many contexts where one theory is as good as the other; however, it is also easy to see that the interpretations used are restrictive and this is exactly what our analysis is detecting. ⁶⁷

Despite this apparent limitation, we can also say a little more about this example. While $ZF+DC+PSP$ and $Inacc$ are generically restrictive with respect to each other, an inspection of the proof of Theorem 42 and the interpretations involved reveals that—underneath the hood—we are really identifying a very close connection between two different but nonetheless similar theories.

Theorem 43. Let $PSP_{min}$ be the theory, $ZFC$ plus the statements:

1. (1) V is the result of collapsing all the L-cardinals below $\omega _{1}$ ;

2. (2) $PSP^{L(\mathbb {R})}$ and $\neg (PSP^{L(\mathbb {R})})^{L[G]}$ for any L-generic G collapsing any proper initial segment of $\omega _{1}$ .

Then there are generic interpretations witnessing that $PSP_{min}$ and $V=L+Inacc$ are generic retractions of each other; i.e., they are generically equivalent.

The idea behind the theory $PSP_{min}$ is to find a way of stating that the universe is formed by collapsing L below $\omega _{1}$ and ensuring that if we had collapsed less than this, then the perfect set property would have failed. This allows us to go back and forth.

Proof. We use the interpretations described in Theorem 42. Let $i:\Sigma _{M\in ctm(PSP_{min})} gen(M,\mathbb {P}_{i})\to ctm(V=L+Inacc)$ be determined by a trivial poset and the interpretation relativising all quantifiers to L. Let $j:\Sigma _{M\in ctm(V=L+Inacc)}gen(M,\mathbb {P}_{j})\to ctm(PSP_{min})$ be determined by the poset $Col(\omega ,<\kappa )$ where $\kappa $ is the least inaccessible cardinal and the interpretation that restricts quantifies to $L(\mathbb {R})$ .

Let M be a countable transitive model of $PSP_{min}$ . Then $i(\langle M,G\rangle )=L^{M}$ . Moreover, $M=L^{M}[H]$ where H is $Col(\omega ,<\omega _{1}^{M})$ generic over $L^{M}$ . Note that this implies that M satisfies $V=L(\mathbb {R})$ . Then it can be seen via Specker’s result that $\omega _{1}^{M}$ is inaccessible in $L^{M}$ and that there are no $L^{M}$ -inaccessibles below $\omega _{1}$ . Thus H is $L^{M}$ -generic over $Col(\omega ,<\kappa )$ where $\kappa =\omega _{1}^{M}$ is what $L^{M}$ believes is the least inaccessible cardinal. Thus $j(L^{M},H)=M$ as required. Let M be a countable transitive model of $V=L+Inacc$ and let G be $Col(\omega ,<\kappa )$ -generic over M where $\kappa $ is the least inaccessible cardinal of M. It can then be seen that $M[G]$ satisfies $V=L(\mathbb {R})$ , so relativising the quantifiers of $M[G]$ to $L(\mathbb {R})$ just gives us $M[G]$ again. In other words $j(\langle M,G\rangle )=M[G]$ . Now using i, we go to $L^{M[G]}$ which is of course M as required.

Informally, this tells that although $V=L+Inacc$ and $ZF+DC+PSP$ are not generic retracts of each other there are slight modifications of those theories that are, in fact, generically equivalent. I think the right way to look at this is to observe that the classical result doesn’t reveal a particularly strong connection between these theories. The obvious generic interpretations lead to some loss of information. Nonetheless, those interpretations do reveal a very deep connection between the modified versions. I submit this is evidence that generic retraction is a natural benchmark for the registering of deep connection between strong set theories.

That all said, looking at the modified theories, a further worry might emerge. It is easy to see that revised theories are themselves restrictive in relation to other theories. For example, both of the theories discussed in Proposition 43 are restrictive with respect to the theory $MC$ . In essence, this is because both theories describe universes that are constructible from a particular set. So although the revised theories are no longer restrictive with respect to each other, they are restrictive with respect to the standard yardstick of interpretative power: the large cardinal hierarchy. However, there is a further natural response to this kind of restrictiveness that emerges from inner model theory: there is a hierarchy of inner models that accommodate larger large cardinals and are thus able to transcend particular levels of restrictiveness. More specifically, an inspection of the proofs of Theorem 42 reveals that the following conditions on L were sufficient for the proof of Theorem 43 to go through:

1. (1) The definition of L can be relativized to particular reals $x\in \mathbb {R}$ to obtain $L[x]$ .

2. (2) For all $x\in \mathbb {R}$ , $L[x]$ is generic invariant (i.e., $L[x]^{V}=L[x]^{V[G]}$ whenever G is set-generic over V).

3. (3) For all $x\in \mathbb {R}$ , $L[x]\models CH$ .

This motivates the following definition.

Definition 44. Suppose $S[x]$ is a class term for class model as defined by a formula $\psi _{S}(y,x)$ of $\mathcal {L}_{\in }$ where x is some set. We say that S is a stable interpretation if $S[x]$ is generic invariant and $CH^{S[x]}$ holds for all $x\in \mathbb {R}$ .

Using this, we can generalize Proposition 43 substantially. First for stable interpretations $S,$ let $PSP_{min}^{S}$ be the theory that generalizes $PSP_{min}$ to S; i.e., we extend $ZFC$ by the statements that: the universe is the collapse of all S-cardinals below $\omega _{1}$ ; $PSP^{L(\mathbb {R})}$ and for all S-generic G that collapse an initial segment of $\omega _{1}$ , $(PSP^{L(\mathbb {R})})^{S[G]}$ does not hold. Now let $K^{DJ}$ be the Dodd–Jensen core model, $L[U]$ be the canonical inner model of a cardinal that is measurable, and let $\mathcal {M}_{n}$ be the canonical model of n-Woodin cardinals. ⁶⁸ Each of these class terms denotes a stable interpretation. For stable interpretations, let us write $V=S$ for the theory extending $ZFC$ by saying that every set is in S. Let us write $\forall x\ x^{\#}\exists $ for the statement that every set’s $\#$ exists. Let us write $\exists MC$ for the statement that there is a measurable cardinal. And let us write $\exists nWC$ to mean that there are n many Woodin cardinals. With this we can then obtain:

Proposition 45. (1) $PSP_{min}^{K^{DJ}}+\forall x\ x^{\#}\exists $ is generically equivalent with $V=K^{DJ}+\forall x\ x^{\#}\exists $ .

(2) $PSP_{min}^{L[U]}+\exists MC$ is generically equivalent with $V=L[U]+\exists MC$ .

(3) $PSP_{min}^{\mathcal {M}_{n}}+\exists nWC$ is generically equivalent with $V=\mathcal {M}_{n}+\exists nWC$ .

Thus we see that the close connection between these theories is preserved as we move up the large cardinal hierarchy using canonical inner models. Note, however, that each of these models also comes with an anti-large cardinal assumption, which will also be restrictive in the sense described in this paper. For example if $V=K^{DJ}$ there are no measurable cardinals, and if $V=L[U]$ there are no Woodin cardinals. Thus, we seem to be limited to using obviously restrictive theories when we look for close connections between theories generalising Proposition 43. The move that allows us to escape from one level of restrictiveness seems to introduce a new level of restrictiveness. Woodin’s work on the ultimate L program might be used to provide a response to this problem [26]. The notion of a weak extender model for $\delta $ is supercompact is intended to generalize the canonical model $L[U]$ for a measurable cardinal to the case of a supercompact cardinal. If such interpretations exist then the following theorem tells us that there is an important sense in which they are compatible with just about any large cardinal assumption.

Theorem 46. [26] Suppose that N is a weak extender model, for $\delta $ , is supercompact and $\gamma>\delta $ is a cardinal in N. Suppose that

$$ \begin{align*} j:V_{\gamma+1}^{N}\to V_{\gamma+1}^{N} \end{align*} $$

is a non-trivial elementary embedding such that $\delta \leq cp(j)$ . Then $j\in N$ .

For a contrast, observe that assuming $0^{\#}$ exists, there is a non-trivial elementary embedding $j:L_{\omega _{1}}\to L_{\omega _{1}}$ ; however, j cannot be in L. This kind of restrictiveness is avoided by weak extender models. For example, if there is a huge cardinal $\kappa $ above a supercompact cardinal $\delta $ , then the theorem above implies that a weak extender model N for $\delta $ being supercompact will also satisfy that $\kappa $ is huge cardinal. ⁶⁹ With this in mind we can offer a generalization of Proposition 43 that essentially would not rule out any large cardinal hypotheses. Suppose N is a class term for a stable interpretation that is also a weak extender model for its least supercompact cardinal being supercompact. Then $V=N$ with the statement that there is a huge cardinal is generically equivalent to $PSP_{min}^{N}$ plus there is a huge cardinal. Moreover, if such models exist then there appears to be no limit to the large cardinal strength that can be added in the place of the already aptly named huge cardinals.

Nonetheless, we should note that this response is still a kind of patch solution. While we regain a means of ascending through the consistency strength hierarchy, we are not really avoiding restrictiveness according to the analysis offered in this paper. Just because the weak extender models (and other inner models) absorb large cardinal strength from the ambient universe, this does not mean that we can use forcing to get back to that ambient universe once we have gone inside. I think the right way to look at this is to say that this is indeed a patch solution, albeit a very natural one. By adopting it, we are taking seriously the idea that the only important structures are those that can be obtained by forcing out from canonical inner models of large cardinal axioms. This is a common idea in inner model theory and it provides a very clean way of organizing extensions of $ZFC$ . However, it is also clear that some models of the theories, which are obtained by forcing from inner models, will be excluded by this perspective. The virtue of our analysis of restrictiveness is that it isolates exactly which models are missing: the information loss. ⁷⁰

Let’s close this discussion by reviewing the upshot of the example. We have taken a prototypical example of an equiconsistency proof involving forcing and asked whether and how it fits our proposed analysis of restrictiveness. We saw that while the analysis is too fine-grained to capture an equivalence between these theories, an inspection of the proof and the interpretations gave rise to modified theories that were generically equivalent. We might think of these theories as providing a means to cut away the loose information that could be lost in translation. Nonetheless, even these modified interpretations were restrictive in relation to large cardinal assumptions, but by generalizing the inner model interpretations used in that proof we were able to regain the relationship with theories of stronger interpretability power.

Example 2

Our second example concerns a counterintuitive case where a version of our analysis indicates restrictiveness. Like the former example, this will reveal more about the limits of our analysis, although in this case we’ll offer a different kind of patch. Rather than modifying the theories, we’ll provide a novel notion of retraction. In particular, we shall see that our analysis says that the axiom of extensionality is restrictive! We first explain how this works and then provide some commentary. Despite the sense of oddity in this result, we shall see that this example yields some useful methodological insights for the further pursuit of this kind of project. Let $ZFC\backslash \{Ext\}$ be $ZFC$ without the axiom of extensionality.

Proposition 47. (1) (essentially [21]) $ZFC$ is an isomorphism-retraction of $ZFC\backslash \{Ext\}$ . ⁷¹

(2) $ZFC\backslash \{Ext\}$ is not an isomorphism retract of $ZFC$ in the category of well-founded models, if there is a transitive model of $ZFC$ .

Note that we are not using generic retraction here. We do this for a simpler presentation. I don’t believe the addition of generic extensions into the machinery will block this; however, forcing without the axiom of extensionality will introduce some non-trivial difficulties that will merely obscure our point. ⁷²

Proof. Let $i:mod(ZFC)\to mod(ZFC\backslash \{Ext\})$ be the identity interpretation. Let $j:mod(ZFC\backslash \{Ext\})\to mod(ZFC)$ be defined through a short sequence of definitions as follows. First let $x\sim y$ if x and y have the same elements. Let $I(x)$ hold if the members of x are closed under $\sim $ ; i.e., whenever $y\in x$ and $z\sim y$ , we have $z\in x$ . Finally, let $H(x)$ hold if x’s members are closed under $\sim $ and there is superset y of x whose members z are subsets of y and such that the members of z are closed under $\sim $ . ⁷³ We then let the domain of the j interpretation be given by $H(x)$ and we interpret $=$ as $\sim $ while preserving the $\in $ -relation. ⁷⁴ It can then be seen that whenever $\mathcal {M}$ is a model of $ZFC$ , $j\circ i(\mathcal {M})\cong \mathcal {M}$ . Thus we have an isomorphism retraction. ⁷⁵ To see that $ZFC\backslash \{Ext\}$ is not a retract of $ZFC$ . Suppose not and fix

$$ \begin{align*} s:mod(ZFC\backslash\{Ext\})\leftrightarrow mod(ZFC):t \end{align*} $$

witnessing this. Now let M be a countable transitive model of $ZFC$ . Generate a model N of $ZFC\backslash \{Ext\}$ from M be adding $\aleph _{1}$ many new elements that have no N-elements, i.e., empty sets. ⁷⁶ Then since we have restricted our attention to well-founded models it can be seen that $s(N)\cong M$ but then there is no way that $s(N)$ can define N since $s(N)$ is countable but N is not. ⁷⁷

Informally, a model of $ZFC\backslash \{Ext\}$ can have any number of different sets that have the same members. If we transform this into a model in which extensionality holds, then these different sets will be identified and there will be no way to recover their distinction. This could appear counterintuitive. Assuming for the sake of argument that there is something restrictive about extensionality, we are probably unlikely to think that it is restrictive in the same way that $V=L$ is. There is something to this though it seems extremely unlikely that there could be some version of $0^{\#}$ for the axiom of extensionality. However, I also think this is a little misleading. The analysis of restrictiveness offered in this paper captures a very natural notion thereof. Moreover, it is clear from the proof above that the axiom of extensionality fits this analysis very well. If we were to blindly deploy our analysis as a tool for axiom selection, then this result would be an obvious bug. I’d prefer to think of it as a feature. We are learning that while our analysis can provide an intuitive understanding of restrictiveness, this cannot be all that is at stake when we come to choose between different extensions of $ZFC$ .

Nonetheless as with the previous example, a plausible response can also be provided. Recalling the interpretation hierarchy described in Definition 8, we saw how to obtain coarser grained notions of equivalence by weakening the relationship that we demand holds between the initial model and the model we obtain by interpreting forth and back. In that spirit, we might wonder if there is a model-theoretic relation that can neutralize the effect highlighted above. The following definition provides such a relation. ⁷⁸

Definition 48. Suppose $\mathcal {M}=\langle M,\in _{\mathcal {M}}\rangle $ and $\mathcal {N}=\langle N,\in _{\mathcal {N}}\rangle $ are models of $\mathcal {L}_{\in }$ . A relation $R\subseteq M\times N$ is a bisimulation if:

1. (1) whenever $x\in _{\mathcal {M}}y$ and $yRy^{*}$ then there is some $xRx^{*}$ such that $x^{*}\in _{\mathcal {N}}y^{*}$ ; and

2. (2) whenever $x^{*}\in _{\mathcal {N}}y^{*}$ and $yRy^{*}$ , then there is some $xRx^{*}$ such that $x\in _{\mathcal {M}}y$ .

Let us say that $\mathcal {M}$ and $\mathcal {N}$ are bisimulatable if there is a bisimulation $R\subseteq M\times N$ such that the domain of R is M and the range of R is N.

A little loosely, if we have a bisimulation between two models, then we are saying that for any element of one model there is a corresponding element of the other model such that they both have the same transitive closure structure if we ignore the fact that some pairs of sets can have the same members. This can also be made sense of in a game theoretic context. We might imagine that player $II$ claims that $\mathcal {M}$ and $\mathcal {N}$ are bisimulatable while I claims they are not. I thus starts play with a challenge by putting forward an element $m_{0}$ of say, $\mathcal {M}$ , they hope to show has no counterpart in $\mathcal {N}$ . $II$ then responds by playing an element $n_{0}$ of $\mathcal {N}$ that they hope to show is a counterpart. I then challenges this by playing an $\mathcal {M}$ -element $m_{1}$ of $m_{0}$ and then $II$ responds with an $\mathcal {N}$ -element $n_{1}$ of $n_{0}$ . Play then continues with player I winning just in case $II$ gets to a position where they can no longer move. It can then be seen that $\mathcal {M}$ and $\mathcal {N}$ are bisimulatable just in case player $II$ has a winning strategy in this game. This allows us to form a new notion of retraction that is immune to the effects of extensionality failure.

Definition 49. Let $T,S$ be theories in $\mathcal {L}_{\in }$ and suppose $t:mod(T)\leftrightarrow mod(S):s$ witness that they are mutually interpretable. We say that T is a bisimulation-retract of S if for all models $\mathcal {M}$ of T, $s\circ t(\mathcal {M})$ is bisimulatable with $\mathcal {M}$ . We say T is bisimulation equivalent if t and s witness that T is a bisimulation retract of S and S is a bisimulation retract of T.

With this notion of retraction, it can then be seen that $ZFC$ is no longer restrictive with respect to $ZFC\backslash \{Ext\}$ .

Proposition 50. $ZFC\backslash \{Ext\}$ is bisimulation equivalent to $ZFC$ .

Thus, we see that there is a method of glossing away the counterintuitive result described above. If we use a more generous notion of equivalence between models, then the restrictive effect of extensionality seems to wash away. This seems like a good thing; however, I think it also warrants a few remarks. The response we’ve offered above might be challenged on the basis that it seems to put a finger on the scales. We obtained a result we didn’t much like and then looked for the nearest instrument we could deploy to ignore it. With that said, it probably sounds less like a good thing. However, rather than attempt to decide this issue, I think it is a better to draw a methodological lesson. Given two theories that we have reason to think share some plausible connection, we should do whatever it takes to formally isolate that connection. This may mean considering modifying the theories we compare—as in our first example, or developing new positions in the interpretability hierarchy—as in the second example, or something else entirely. When this method works, we inevitably learn two things. In one direction, we learn more about the nature of the connection between the two theories. In the other, these results yield valuable insights as to the boundaries upon interpretation as a tool for theory comparison. I believe that pursuing this line of attack further provides the right methodology for better understanding what we mean when we say a theory is restrictive or that two theories are equivalent.

Concluding remarks

In this paper, I’ve offered a formal analysis of what it means for one theory to be restrictive in relation to another. The account is based on the algebraic notion of retraction in the category of theories. Informally speaking, a theory T is restrictive with respect to S if there is a uniform means of depositing the models of T among the models of S and recovering them, but there is no corresponding means for models of S: information is lost. Moreover, the account offered in Section 4 provides a way of accommodating contemporary set-theoretic practice by putting generic extension on an equal footing with inner model constructions. Evidence pushing us in the direction of this approach was then provided in Section 3, where we showed that some seemingly plausible weakenings of our approach did not live up to the goals of their motivating stories. The analysis offered in this paper was then tested on some simple examples that illuminated more about what can be expected from a retraction analysis of restrictiveness among theories. I think these results are merely a beginning.