Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-01-13T23:30:25.770Z Has data issue: false hasContentIssue false
  • English
  • Français

ULTIMATE TRUTH VIS-À-VIS STABLE TRUTH

Published online by Cambridge University Press:  01 June 2008

P. D. WELCH
P. D. WELCH*
Affiliation:
School of Mathematics, University of Bristol
*
*SCHOOL OF MATHEMATICS, UNIVERSITY OF BRISTOL, BRISTOL BS8 1TW, UK. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that the set of ultimately true sentences in Hartry Field's Revenge-immune solution model to the semantic paradoxes is recursively isomorphic to the set of stably true sentences obtained in Hans Herzberger's revision sequence starting from the null hypothesis. 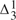We further remark that this shows that a substantial subsystem of second-order number theory is needed to establish the semantic values of sentences in Field's relative consistency proof of his theory over the ground model of the standard natural numbers: -CA0 (second-order number theory with a 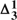-comprehension axiom scheme) is insufficient. We briefly consider his claim to have produced a ‘revenge-immune’ solution to the semantic paradoxes by introducing this conditional. We remark that the notion of a ‘determinately true’ operator can be introduced in other settings.

Type
Research Article
Information
The Review of Symbolic Logic , Volume 1 , Issue 1 , June 2008 , pp. 126 - 142
Copyright
Copyright © Association for Symbolic Logic 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Barwise, K. (1975). Admissible Sets and Structures, Perspectives in Mathematical Logic. Berlin: Springer Verlag.CrossRefGoogle Scholar
Burgess, J. (1986). The truth is never simple. Journal for Symbolic Logic, 51(3), 663–681.CrossRefGoogle Scholar
Devlin, K. (1984). Constructibility, Perspectives in Mathematical Logic. Berlin, Heidelberg: Springer Verlag.Google Scholar
Field, H. (2003). A revenge-immune solution to the semantic paradoxes. Journal of Philosophical Logic, 32(3), 139–177.CrossRefGoogle Scholar
Field, H. (2008). Solving the Paradoxes, escaping revenge. In Beall, J., editor, The Revenge of the Liar. Oxford: Oxford University Press, pp. 78–144.Google Scholar
Gupta, A., & Belnap, N. (1993). The Revision Theory of Truth. Cambridge: MIT Press.CrossRefGoogle Scholar
Hamkins, J. D., & Lewis, A. (2000). Infinite time Turing machines. Journal of Symbolic Logic, 65(2), 567–604.CrossRefGoogle Scholar
Herzberger, H. (1982a). Naive semantics and the Liar paradox. Journal of Philosophy, 79, 479–497.CrossRefGoogle Scholar
Herzberger, H. (1982b). Notes on naive semantics. Journal of Philosophical Logic, 11, 61–102.CrossRefGoogle Scholar
Kreutzer, S. (2002). Partial fixed point logic on infinite structures. In Bradfield, J., editor, Annual Conference of the European Association for Computer Science Logic (CSL), Vol. 2471, Lecture Notes in Computer Science. Berlin: Springer, pp. 337–351.Google Scholar
Kripke, S. (1975). Outline of a theory of truth. Journal of Philosophy, 72, 690–716.CrossRefGoogle Scholar
Leitgeb, H. (2006). On Field's ‘Solving the paradoxes, escaping revenge’. In Beall, J., editor, The Revenge of the Liar. Oxford: Oxford University Press, pp. 159–183.Google Scholar
McGee, V. (1991). Truth, Vagueness, and Paradox: An Essay on the Logic of Truth. Indianapolis: Hackett.Google Scholar
Moschovakis, Y. (1974). Elementary Induction on Abstract Structures, Vol. 77, Studies in Logic Series. Amsterdam, The Netherlands: North-Holland.Google Scholar
Rogers, H. (1967). Recursive Function Theory, Higher Mathematics. New York: McGraw.Google Scholar
Simpson, S. (1999). Subsystems of Second Order Arithmetic, Perspectives in Mathematical Logic. Berlin: Springer.CrossRefGoogle Scholar
Welch, P. D. (2000). Eventually infinite time Turing degrees: Infinite time decidable reals. Journal for Symbolic Logic, 65(3), 1193–1203.Google Scholar