Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T11:59:55.420Z Has data issue: false hasContentIssue false
  • English
  • Français

SUBSTRUCTURAL INQUISITIVE LOGICS

Published online by Cambridge University Press:  01 February 2019

VÍT PUNČOCHÁŘ
VÍT PUNČOCHÁŘ*
Affiliation:
Institute of Philosophy, Czech Academy of Sciences
*
*INSTITUTE OF PHILOSOPHY CZECH ACADEMY OF SCIENCES JILSKÁ 1, 110 00 PRAGUE, CZECH REPUBLIC E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper shows that any propositional logic that extends a basic substructural logic BSL (a weak, nondistributive, nonassociative, and noncommutative version of Full Lambek logic with a paraconsistent negation) can be enriched with questions in the style of inquisitive semantics and logic. We introduce a relational semantic framework for substructural logics that enables us to define the notion of an inquisitive extension of λ, denoted as 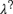${\lambda ^?}$, for any logic λ that is at least as strong as BSL. A general theory of these “inquisitive extensions” is worked out. In particular, it is shown how to axiomatize 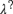${\lambda ^?}$, given the axiomatization of λ. Furthermore, the general theory is applied to some prominent logical systems in the class: classical logic Cl, intuitionistic logic Int, and t-norm based fuzzy logics, including for example Łukasiewicz fuzzy logic Ł. For the inquisitive extensions of these logics, axiomatization is provided and a suitable semantics found.

Keywords

03B47inquisitive semanticslogic of questionssubstructural logicclassical logicintuitionistic logicfuzzy logic
Type
Research Article
Information
The Review of Symbolic Logic , Volume 12 , Issue 2 , June 2019 , pp. 296 - 330
Copyright
Copyright © Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Bílkova, M., Majer, O., & Peliš, M. (2016). Epistemic logics for skeptical agents. Journal of Logic and Computation, 26, 1815–1841.CrossRefGoogle Scholar
Ciardelli, I. (2016a). Dependency as question entailment. In Abramsky, S., Kontinen, J., Väänänen, J., and Vollmer, H., editors. Dependence Logic: Theory and Applications. Basel: Birkhäuser, pp. 129–181.CrossRefGoogle Scholar
Ciardelli, I. (2016b). Questions in Logic. Ph.D. Thesis, University of Amsterdam.Google Scholar
Ciardelli, I. (2018). Questions as information types. Synthese, 195, 321–365.CrossRefGoogle Scholar
Ciardelli, I., Groenendijk, J., & Roelofsen, F. (2013). Inquisitive semantics: A new notion of meaning. Language and Linguistics Compass, 7, 459–476.CrossRefGoogle Scholar
Ciardelli, I. & Roelofsen, F. (2011). Inquisitive logic. Journal of Philosophical Logic, 40, 55–94.CrossRefGoogle Scholar
Došen, K. (1988). Sequent systems and groupoid models, Part 1. Studia Logica, 47, 353–385.CrossRefGoogle Scholar
Došen, K. (1989). Sequent systems and groupoid models, Part 2. Studia Logica, 48, 41–65.CrossRefGoogle Scholar
Dunn, J. M. (1993). Star and perp: Two treatments of negation. Philosophical Perspectives, 7, 331–357.CrossRefGoogle Scholar
Düntsch, I. & Winter, M. (2005). A representation theorem for boolean contact algebras. Theoretical Computer Science (B), 347, 498–512.CrossRefGoogle Scholar
Fine, K. (1974). Models for entailment. Journal of Philosophical Logic, 3, 347–372.CrossRefGoogle Scholar
Fine, K. (2014). Truth-maker semantics for intuitionistic logic. Journal of Philosophical Logic, 43, 221–246.CrossRefGoogle Scholar
Galatos, N., Jipsen, P., Kowalski, T., & Ono, H. (2007). Residuated Lattices: An Algebraic Glimpse at Substructural Logics. Amsterdam: Elsevier.Google Scholar
Groenendijk, J. & Stokhof, M. (1997). Questions. In van Benthem, J. and ter Meulen, A., editors. Handbook of Logic and Language. Amsterdam: Elsevier, pp. 1055–1124.CrossRefGoogle Scholar
Hájek, P. (1998). Metamathematics of Fuzzy Logic. Dordrecht: Kluwer.CrossRefGoogle Scholar
Harrah, D. (2002). The logic of questions. In Gabbay, D. M. and Guenthner, F., editors. Handbook of Philosophical Logic , Vol. 8. Dordrecht: Springer, pp. 1–60.Google Scholar
Lambek, J. (1958). The mathematics of sentence structure. The American Mathematical Monthly, 65, 154–170.CrossRefGoogle Scholar
Lambek, J. (1961). On the calculus of syntactic types. In Jakobson, R., editor. Structure of Language and Its Mathematical Aspects. Providence, RI: American Mathematical Society, pp. 166–178.CrossRefGoogle Scholar
Ono, H. & Komori, Y. (1985). Logics without the contraction rule. Journal of Symbolic Logic, 50, 169–201.CrossRefGoogle Scholar
Paoli, F. (2002). Substructural Logics: A Primer. Dordrecht: Kluwer.CrossRefGoogle Scholar
Peliš, M. (2016). Inferences with Ignorance: Logics of Questions (Inferential Erotetic Logic & Erotetic Epistemic Logic). Praha: Karolinum.Google Scholar
Punčochář, V. (2016). A generalization of inquisitive semantics. Journal of Philosophical Logic, 45, 399–428.CrossRefGoogle Scholar
Punčochář, V. (2017). Algebras of information states. Journal of Logic and Computation, 27, 1643–1675.Google Scholar
Rescher, N. (1966). The Logic of Commands. London: Routledge.Google Scholar
Restall, G. (2000). An Introduction to Substructural Logics. London: Routledge.CrossRefGoogle Scholar
Sedlár, I. (2015). Substructural epistemic logics. Journal of Applied Non-Classical Logics, 25, 256–285.CrossRefGoogle Scholar
Urquhart, A. (1972). Semantics for relevant logics. The Journal of Symbolic Logic, 37, 159–169.CrossRefGoogle Scholar
Vranas, P. B. M. (2010). In defense of imperative inference. Journal of Philosophical Logic, 39, 59–71.CrossRefGoogle Scholar
Wansing, H. (1993). Informational interpretation of substructural logics. Journal of Logic, Language, and Information, 2, 285–308.CrossRefGoogle Scholar
Wiśniewski, A. (1995). The Posing of Questions: Logical Foundations of Erotetic Inferences. Dordrecht: Kluwer Academic Publishers.CrossRefGoogle Scholar
Wiśniewski, A. (2013). Questions, Inferences, and Scenarios. London: College Publications.Google Scholar
Yang, E. (2014). Algebraic Kripke-style semantics for relevance logics. Journal of Philosophical Logic, 43, 803–826.CrossRefGoogle Scholar