Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T19:32:21.906Z Has data issue: false hasContentIssue false
  • English
  • Français

SOME OBSERVATIONS ON TRUTH HIERARCHIES

Published online by Cambridge University Press:  02 January 2014

P. D. WELCH
P. D. WELCH*
Affiliation:
School of Mathematics, University of Bristol
*
*SCHOOL OF MATHEMATICS UNIVERSITY OF BRISTOL ENGLAND BS8 1TW E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show how in the hierarchies 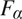${F_\alpha }$ of Fieldian truth sets, and Herzberger’s 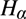${H_\alpha }$ revision sequence starting from any hypothesis for 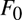${F_0}$ (or 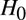${H_0}$) that essentially each 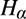${H_\alpha }$ (or 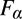${F_\alpha }$) carries within it a history of the whole prior revision process.

As applications (1) we provide a precise representation for, and a calculation of the length of, possible path independent determinateness hierarchies of Field’s (2003) construction with a binary conditional operator. (2) We demonstrate the existence of generalized liar sentences, that can be considered as diagonalizing past the determinateness hierarchies definable in Field’s recent models. The ‘defectiveness’ of such diagonal sentences necessarily cannot be classified by any of the determinateness predicates of the model. They are ‘ineffable liars’. We may consider them a response to the claim of Field (2003) that ‘the conditional can be used to show that the theory is not subject to “revenge problems”.’

Type
Research Article
Information
The Review of Symbolic Logic , Volume 7 , Issue 1 , March 2014 , pp. 1 - 30
Copyright
Copyright © Association for Symbolic Logic 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Boolos, G. (1970). On the semantics of the constructible levels. Zeitschrift für Mathematische Logik, 16, 139–148.CrossRefGoogle Scholar
Burgess, J. P. (1986). The truth is never simple. Journal of Symbolic Logic, 51(3), 663–681.Google Scholar
Devlin, K. (1984). Constructibility Perspectives in Mathematical Logic. Berlin: Springer Verlag.Google Scholar
Field, H. (2003). A revenge-immune solution to the semantic paradoxes. Journal of Philosophical Logic, 32(3), 139–177.CrossRefGoogle Scholar
Field, H. (2008a). Saving Truth from Paradox. Oxford: Oxford University Press.Google Scholar
Field, H. (2008b). Solving the paradoxes, escaping revenge. In Beall, J. C., editor. The Revenge of the Liar. Oxford: Oxford University Press.Google Scholar
Field, H. (2011). Responses at APA session Dec. 2009. Review of Symbolic Logic, 4(3), 360–366.Google Scholar
Friedman, S.-D. & Welch, P.D. (2007). Two observations concerning infinite time Turing machines. In Dimitriou, I., editor. BIWOC 2007 Report, Bonn, January 2007. Hausdorff Centre for Mathematics. pp. 44–47. Available from: http://www.logic.univie.ac.at/sdf/papers/joint.philip.ps.Google Scholar
Gupta, A., & Belnap, N. (1993). The Revision Theory of Truth. Cambridge, MA: M.I.T. Press.CrossRefGoogle Scholar
Hamkins, J. D., & Lewis, A. (2000). Infinite time Turing machines. Journal of Symbolic Logic, 65(2), 567–604.Google Scholar
Herzberger, H. G. (1982a). Naive semantics and the Liar paradox. Journal of Philosophy, 79, 479–497.CrossRefGoogle Scholar
Herzberger, H. G. (1982b). Notes on naive semantics. Journal of Philosophical Logic, 11, 61–102.CrossRefGoogle Scholar
Horsten, L., Leigh, G., Leitgeb, H., & Welch, P. D. (2012). Revision revisited. Review of Symbolic Logic, 5, 642–664.Google Scholar
Jensen, R. B. (1972). The fine structure of the constructible hierarchy. Annals of Mathematical Logic, 4, 229–308.CrossRefGoogle Scholar
Kripke, S. (1975). Outline of a theory of truth. Journal of Philosophy, 72, 690–716.Google Scholar
Martin, D. A. (1997). Revision and its rivals. Philosophical Issues, 8, 407–418.CrossRefGoogle Scholar
Martin, D. A. (2011). Field’s saving truth from paradox: Some things it doesn’t do. Review of Symbolic Logic, 4(3), 339–347.Google Scholar
Odifreddi, P.-G. (1989). Classical Recursion Theory: The Theory of Functions and Sets of Natural Numbers. Studies in Logic. Amsterdam, Netherland: North-Holland.Google Scholar
Rogers, H. (1967). Recursive Function Theory. Higher Mathematics. New York: McGraw.Google Scholar
Sacks, G. E. (1990). Higher Recursion Theory. Perspectives in Mathematical Logic. Berlin: Springer Verlag.Google Scholar
Soare, R. I. (1987). Recursively Enumerable Sets and Degrees. Perspectives in Mathematical Logic. Berlin: Springer.CrossRefGoogle Scholar
Welch, P. D. (2008). Ultimate truth vis à vis stable truth. Review of Symbolic Logic, 1(1), 126–142.Google Scholar
Welch, P. D. (2009a). Characteristics of discrete transfinite Turing machine models: Halting times, stabilization times, and normal form theorems. Theoretical Computer Science, 410, 426–442.Google Scholar
Welch, P. D. (2009b). Games for truth. Bulletin of Symbolic Logic, 15(4), 410–427.Google Scholar
Welch, P. D. (2011). Truth, logical validity, and determinateness: A commentary on Field’s saving truth from paradox. Review of Symbolic Logic, 4(3), 348–359.CrossRefGoogle Scholar