Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-08T05:11:31.174Z Has data issue: false hasContentIssue false
  • English
  • Français

EXPRESSIVE LIMITATIONS OF NAÏVE SET THEORY IN LP AND MINIMALLY INCONSISTENT LP.

Published online by Cambridge University Press:  21 February 2014

NICK THOMAS
NICK THOMAS*
Affiliation:
University of Connecticut
*
*DEPARTMENT OF PHILOSOPHY UNIVERSITY OF CONNECTICUT, USA E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We give some negative results on the expressiveness of naïve set theory (NS) in LP and in the four variants of minimally inconsistent LP defined in Crabbé (2011): 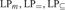${\rm{L}}{{\rm{P}}_m},{\rm{L}}{{\rm{P}}_ = },{\rm{L}}{{\rm{P}}_ \subseteq }$, and 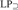${\rm{L}}{{\rm{P}}_ \supseteq }$. We show that NS in LP cannot prove the existence of sets that behave like singleton sets, Cartesian pairs, or infinitely ascending linear orders. We show that NS is close to trivial in 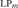${\rm{L}}{{\rm{P}}_m}$ and 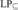${\rm{L}}{{\rm{P}}_ \subseteq }$, in the sense that its only minimally inconsistent model is a one-element model. We show that NS in 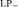${\rm{L}}{{\rm{P}}_ = }$ and 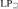${\rm{L}}{{\rm{P}}_ \supseteq }$ has the same limitations we give for NS in LP.

Type
Research Article
Information
The Review of Symbolic Logic , Volume 7 , Issue 2 , June 2014 , pp. 341 - 350
Copyright
Copyright © Association for Symbolic Logic 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Beall, J. C. (2011). Multiple conclusion LP and default classicality. The Review of Symbolic Logic, 4(2), 326–336.CrossRefGoogle Scholar
Beall, J. C. (201+). A simple approach towards recapturing consistent theories in paraconsistent settings. The Review of Symbolic Logic. To appear.Google Scholar
Crabbé, M. (2011). Reassurance for the logic of paradox. The Review of Symbolic Logic, 4(3), 479–285.CrossRefGoogle Scholar
Priest, G. (1991). Minimally inconsistent LP. Studia Logica, 50(2), 321–331.CrossRefGoogle Scholar
Priest, G. (2006). In Contradiction: A Study of the Transconsistent (second edition). Oxford, UK: Oxford University Press.CrossRefGoogle Scholar
Restall, G. (1992). A note on naïve set theory in LP. Notre Dame Journal of Formal Logic, 33(3), 422–432.CrossRefGoogle Scholar
Thomas, N. (2013). Recapturing Classical Mathematics in Paraconsistent Set Theory. Available from http://sites.google.com/a/uconn.edu/nick-thomas/.Google Scholar