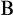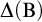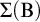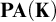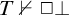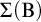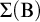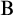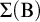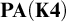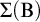1 Introduction
A theory or a logic T is said to have the disjunction property (
![]() $\mathrm {DP}$
) if for any sentences
$\mathrm {DP}$
) if for any sentences
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
in the language of T, if
$\psi $
in the language of T, if
![]() $T \vdash \varphi \lor \psi $
, then
$T \vdash \varphi \lor \psi $
, then
![]() $T \vdash \varphi $
or
$T \vdash \varphi $
or
![]() $T \vdash \psi $
. This is a property that may be considered to represent the constructivity of intuitionistic logic. Gödel [Reference Gödel and Feferman8] noted that the intuitionistic propositional logic has
$T \vdash \psi $
. This is a property that may be considered to represent the constructivity of intuitionistic logic. Gödel [Reference Gödel and Feferman8] noted that the intuitionistic propositional logic has
![]() $\mathrm {DP}$
. Gentzen [Reference Gentzen7] and Kleene [Reference Kleene14] proved that the intuitionistic quantified logic and Heyting arithmetic
$\mathrm {DP}$
. Gentzen [Reference Gentzen7] and Kleene [Reference Kleene14] proved that the intuitionistic quantified logic and Heyting arithmetic
![]() $\mathbf {HA}$
have
$\mathbf {HA}$
have
![]() $\mathrm {DP}$
, respectively. A property in arithmetic that is related to
$\mathrm {DP}$
, respectively. A property in arithmetic that is related to
![]() $\mathrm {DP}$
is the (numerical) existence property. We say that a theory T of arithmetic has the existence property (
$\mathrm {DP}$
is the (numerical) existence property. We say that a theory T of arithmetic has the existence property (
![]() $\mathrm {EP}$
) if for any formula
$\mathrm {EP}$
) if for any formula
![]() $\varphi (x)$
that has no free variables except
$\varphi (x)$
that has no free variables except
![]() $x$
, if
$x$
, if
![]() $T \vdash \exists x \varphi (x)$
, then
$T \vdash \exists x \varphi (x)$
, then
![]() $T \vdash \varphi (\overline {n})$
for some natural number
$T \vdash \varphi (\overline {n})$
for some natural number
![]() $n$
. Here
$n$
. Here
![]() $\overline {n}$
is the numeral for
$\overline {n}$
is the numeral for
![]() $n$
. Kleene [Reference Kleene14] also proved that
$n$
. Kleene [Reference Kleene14] also proved that
![]() $\mathbf {HA}$
has
$\mathbf {HA}$
has
![]() $\mathrm {EP}$
. Moreover, Friedman [Reference Friedman5] proved that for any recursively enumerable (r.e.) extension T of
$\mathrm {EP}$
. Moreover, Friedman [Reference Friedman5] proved that for any recursively enumerable (r.e.) extension T of
![]() $\mathbf {HA}$
, T has
$\mathbf {HA}$
, T has
![]() $\mathrm {DP}$
if and only if T has
$\mathrm {DP}$
if and only if T has
![]() $\mathrm {EP}$
.
$\mathrm {EP}$
.
A similar situation has been shown to be true for modal arithmetic. Modal arithmetic is a framework of arithmetic equipped with the unary modal operator
![]() $\Box $
. Let
$\Box $
. Let
![]() $\mathcal {L}_A$
and
$\mathcal {L}_A$
and
![]() $\mathcal {L}_A(\Box )$
be the languages of arithmetic and modal arithmetic, respectively. A prominent
$\mathcal {L}_A(\Box )$
be the languages of arithmetic and modal arithmetic, respectively. A prominent
![]() $\mathcal {L}_A(\Box )$
-theory of modal arithmetic is
$\mathcal {L}_A(\Box )$
-theory of modal arithmetic is
![]() $\mathbf {EA}$
(epistemic arithmetic) which is obtained by adding
$\mathbf {EA}$
(epistemic arithmetic) which is obtained by adding
![]() $\mathbf {S4}$
into Peano arithmetic
$\mathbf {S4}$
into Peano arithmetic
![]() $\mathbf {PA}$
. The theory
$\mathbf {PA}$
. The theory
![]() $\mathbf {EA}$
was independently introduced by Shapiro [Reference Shapiro21] and Reinhardt [Reference Reinhardt19, Reference Reinhardt20]. In this framework,
$\mathbf {EA}$
was independently introduced by Shapiro [Reference Shapiro21] and Reinhardt [Reference Reinhardt19, Reference Reinhardt20]. In this framework,
![]() $\Box $
is intended to represent knowability or informal provability, and the language
$\Box $
is intended to represent knowability or informal provability, and the language
![]() $\mathcal {L}_A(\Box )$
has the expressive power to make analyses about these concepts. Moreover, it was shown that
$\mathcal {L}_A(\Box )$
has the expressive power to make analyses about these concepts. Moreover, it was shown that
![]() $\mathbf {HA}$
is faithfully embeddable into
$\mathbf {HA}$
is faithfully embeddable into
![]() $\mathbf {EA}$
via Gödel’s translation (cf. [Reference Flagg and Friedman4, Reference Goodman9, Reference Shapiro21]). This result verifies Shapiro’s suggestion that
$\mathbf {EA}$
via Gödel’s translation (cf. [Reference Flagg and Friedman4, Reference Goodman9, Reference Shapiro21]). This result verifies Shapiro’s suggestion that
![]() $\mathbf {EA}$
is a system about both classical and intuitionistic mathematics. From his suggestion,
$\mathbf {EA}$
is a system about both classical and intuitionistic mathematics. From his suggestion,
![]() $\mathbf {EA}$
may possess some constructive properties. A theory or a logic T is said to have the modal disjunction property (
$\mathbf {EA}$
may possess some constructive properties. A theory or a logic T is said to have the modal disjunction property (
![]() $\mathrm {MDP}$
) if for any
$\mathrm {MDP}$
) if for any
![]() $\mathcal {L}_A(\Box )$
-sentences
$\mathcal {L}_A(\Box )$
-sentences
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
, if
$\psi $
, if
![]() $T \vdash \Box \varphi \lor \Box \psi $
, then
$T \vdash \Box \varphi \lor \Box \psi $
, then
![]() $T \vdash \varphi $
or
$T \vdash \varphi $
or
![]() $T \vdash \psi $
. Also, T is said to have the modal existence property (
$T \vdash \psi $
. Also, T is said to have the modal existence property (
![]() $\mathrm {MEP}$
) if for any
$\mathrm {MEP}$
) if for any
![]() $\mathcal {L}_A(\Box )$
-formula
$\mathcal {L}_A(\Box )$
-formula
![]() $\varphi (x)$
that has no free variables except
$\varphi (x)$
that has no free variables except
![]() $x$
, if
$x$
, if
![]() $T \vdash \exists x \Box \varphi (x)$
, then
$T \vdash \exists x \Box \varphi (x)$
, then
![]() $T \vdash \varphi (\overline {n})$
for some natural number
$T \vdash \varphi (\overline {n})$
for some natural number
![]() $n$
. Then, Shapiro [Reference Shapiro21] proved that
$n$
. Then, Shapiro [Reference Shapiro21] proved that
![]() $\mathbf {EA}$
has both
$\mathbf {EA}$
has both
![]() $\mathrm {MDP}$
and
$\mathrm {MDP}$
and
![]() $\mathrm {MEP}$
. Moreover, Friedman and Sheard [Reference Friedman and Sheard6] proved that for any r.e.
$\mathrm {MEP}$
. Moreover, Friedman and Sheard [Reference Friedman and Sheard6] proved that for any r.e.
![]() $\mathcal {L}_A(\Box )$
-theory T extending
$\mathcal {L}_A(\Box )$
-theory T extending
![]() $\mathbf {EA}$
, T has
$\mathbf {EA}$
, T has
![]() $\mathrm {MDP}$
if and only if T has
$\mathrm {MDP}$
if and only if T has
![]() $\mathrm {MEP}$
.Footnote
1
$\mathrm {MEP}$
.Footnote
1
In the case of classical logic,
![]() $\mathrm {DP}$
is related to the completeness of theories. Indeed, it is easy to see that a consistent theory T based on classical logic has
$\mathrm {DP}$
is related to the completeness of theories. Indeed, it is easy to see that a consistent theory T based on classical logic has
![]() $\mathrm {DP}$
if and only if T is complete. Hence, Gödel–Rosser’s first incompleteness theorem is restated as follows: For any consistent r.e. extension T of
$\mathrm {DP}$
if and only if T is complete. Hence, Gödel–Rosser’s first incompleteness theorem is restated as follows: For any consistent r.e. extension T of
![]() $\mathbf {PA}$
, T does not have
$\mathbf {PA}$
, T does not have
![]() $\mathrm {DP}$
. In this context, Gödel–Rosser’s first incompleteness theorem can be strengthened. For a class
$\mathrm {DP}$
. In this context, Gödel–Rosser’s first incompleteness theorem can be strengthened. For a class
![]() $\Gamma $
of formulas, we say that a theory T has the
$\Gamma $
of formulas, we say that a theory T has the
![]() $\Gamma $
-disjunction property (
$\Gamma $
-disjunction property (
![]() $\Gamma $
-
$\Gamma $
-
![]() $\mathrm {DP}$
) if for any
$\mathrm {DP}$
) if for any
![]() $\Gamma $
sentences
$\Gamma $
sentences
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
, if
$\psi $
, if
![]() $T \vdash \varphi \lor \psi $
, then
$T \vdash \varphi \lor \psi $
, then
![]() $T \vdash \varphi $
or
$T \vdash \varphi $
or
![]() $T \vdash \psi $
. Also, T is said to have the
$T \vdash \psi $
. Also, T is said to have the
![]() $\Gamma $
-existence property (
$\Gamma $
-existence property (
![]() $\Gamma $
-
$\Gamma $
-
![]() $\mathrm {EP}$
) if for any
$\mathrm {EP}$
) if for any
![]() $\Gamma $
formula
$\Gamma $
formula
![]() $\varphi (x)$
that has no free variables except
$\varphi (x)$
that has no free variables except
![]() $x$
, if
$x$
, if
![]() $T \vdash \exists x \varphi (x)$
, then
$T \vdash \exists x \varphi (x)$
, then
![]() $T \vdash \varphi (\overline {n})$
for some natural number
$T \vdash \varphi (\overline {n})$
for some natural number
![]() $n$
. Then, it is shown that for any consistent r.e. extension T of
$n$
. Then, it is shown that for any consistent r.e. extension T of
![]() $\mathbf {PA}$
, T does not have
$\mathbf {PA}$
, T does not have
![]() $\Pi _1$
-
$\Pi _1$
-
![]() $\mathrm {DP}$
(see [Reference Jensen and Ehrenfeucht13]). On the other hand, for extensions of
$\mathrm {DP}$
(see [Reference Jensen and Ehrenfeucht13]). On the other hand, for extensions of
![]() $\mathbf {PA}$
, a similar situation to that of
$\mathbf {PA}$
, a similar situation to that of
![]() $\mathrm {DP}$
and
$\mathrm {DP}$
and
![]() $\mathrm {EP}$
in intuitionistic logic has been shown to hold. That is, it is known that
$\mathrm {EP}$
in intuitionistic logic has been shown to hold. That is, it is known that
![]() $\mathbf {PA}$
has both
$\mathbf {PA}$
has both
![]() $\Sigma _1$
-
$\Sigma _1$
-
![]() $\mathrm {DP}$
and
$\mathrm {DP}$
and
![]() $\Sigma _1$
-
$\Sigma _1$
-
![]() $\mathrm {EP}$
. Moreover, Guaspari [Reference Guaspari10] proved that
$\mathrm {EP}$
. Moreover, Guaspari [Reference Guaspari10] proved that
![]() $\Sigma _1$
-
$\Sigma _1$
-
![]() $\mathrm {DP}$
,
$\mathrm {DP}$
,
![]() $\Sigma _1$
-
$\Sigma _1$
-
![]() $\mathrm {EP}$
, and the
$\mathrm {EP}$
, and the
![]() $\Sigma _1$
-soundness are pairwise equivalent for any consistent r.e. extension of
$\Sigma _1$
-soundness are pairwise equivalent for any consistent r.e. extension of
![]() $\mathbf {PA}$
.
$\mathbf {PA}$
.
In the usual proof of the incompleteness theorems, a provability predicate
![]() $\mathrm {Pr}_T(x)$
, that is, a
$\mathrm {Pr}_T(x)$
, that is, a
![]() $\Sigma _1$
formula weakly representing the provability relation of a theory T plays an important role. Besides the context in which
$\Sigma _1$
formula weakly representing the provability relation of a theory T plays an important role. Besides the context in which
![]() $\Box $
is intended as informal provability, a modal logical study of the notion of formalized provability has been developed by interpreting
$\Box $
is intended as informal provability, a modal logical study of the notion of formalized provability has been developed by interpreting
![]() $\Box $
in terms of
$\Box $
in terms of
![]() $\mathrm {Pr}_T(x)$
. One of the important results of this study is Solovay’s arithmetical completeness theorem which states that if T is
$\mathrm {Pr}_T(x)$
. One of the important results of this study is Solovay’s arithmetical completeness theorem which states that if T is
![]() $\Sigma _1$
-sound, then the propositional modal logic
$\Sigma _1$
-sound, then the propositional modal logic
![]() $\mathbf {GL}$
is exactly the logic of all T-verifiable principles [Reference Solovay22]. In this framework,
$\mathbf {GL}$
is exactly the logic of all T-verifiable principles [Reference Solovay22]. In this framework,
![]() $\mathrm {MDP}$
also makes sense. It is known that
$\mathrm {MDP}$
also makes sense. It is known that
![]() $\mathbf {GL}$
enjoys
$\mathbf {GL}$
enjoys
![]() $\mathrm {MDP}$
. Rather than corresponding to some constructive property, this fact corresponds to the fact that if T is
$\mathrm {MDP}$
. Rather than corresponding to some constructive property, this fact corresponds to the fact that if T is
![]() $\Sigma _1$
-sound, then
$\Sigma _1$
-sound, then
![]() $T \vdash \mathrm {Pr}_{T}(\ulcorner \varphi \urcorner ) \lor \mathrm {Pr}_{T}(\ulcorner \psi \urcorner )$
implies
$T \vdash \mathrm {Pr}_{T}(\ulcorner \varphi \urcorner ) \lor \mathrm {Pr}_{T}(\ulcorner \psi \urcorner )$
implies
![]() $T \vdash \varphi $
or
$T \vdash \varphi $
or
![]() $T \vdash \psi $
.
$T \vdash \psi $
.
Our motivation for the research in the present paper is to provide a unified viewpoint on
![]() $\mathrm {MDP}$
and
$\mathrm {MDP}$
and
![]() $\Gamma $
-
$\Gamma $
-
![]() $\mathrm {DP}$
, which have been discussed in different contexts and frameworks. In particular, we would like to unify the arguments on
$\mathrm {DP}$
, which have been discussed in different contexts and frameworks. In particular, we would like to unify the arguments on
![]() $\Box $
as an informal provability and
$\Box $
as an informal provability and
![]() $\Box $
as a provability predicate. For this purpose, instead of fixing a modal logic such as
$\Box $
as a provability predicate. For this purpose, instead of fixing a modal logic such as
![]() $\mathbf {S4}$
or
$\mathbf {S4}$
or
![]() $\mathbf {GL}$
, we discuss the theory
$\mathbf {GL}$
, we discuss the theory
![]() $\mathbf {PA}(L)$
obtained by adding an arbitrary normal modal logic L to
$\mathbf {PA}(L)$
obtained by adding an arbitrary normal modal logic L to
![]() $\mathbf {PA}$
. In particular,
$\mathbf {PA}$
. In particular,
![]() $\mathbf {K4}$
is a common sublogic of
$\mathbf {K4}$
is a common sublogic of
![]() $\mathbf {S4}$
and
$\mathbf {S4}$
and
![]() $\mathbf {GL}$
, and thus an investigation for extensions of
$\mathbf {GL}$
, and thus an investigation for extensions of
![]() $\mathbf {PA}(\mathbf {K4})$
would be applicable to both of the two different interpretations of
$\mathbf {PA}(\mathbf {K4})$
would be applicable to both of the two different interpretations of
![]() $\Box $
. For example, we prove that for any r.e.
$\Box $
. For example, we prove that for any r.e.
![]() $\mathcal {L}_A(\Box )$
-theory T extending
$\mathcal {L}_A(\Box )$
-theory T extending
![]() $\mathbf {PA}(\mathbf {K4})$
, T has
$\mathbf {PA}(\mathbf {K4})$
, T has
![]() $\mathrm {MDP}$
if and only if T has
$\mathrm {MDP}$
if and only if T has
![]() $\mathrm {MEP}$
. This is a strengthening of the above mentioned form of Friedman and Sheard’s result.
$\mathrm {MEP}$
. This is a strengthening of the above mentioned form of Friedman and Sheard’s result.
We would also like to analyze the possibility of applying existing methods for studying properties such as
![]() $\Gamma $
-
$\Gamma $
-
![]() $\mathrm {DP}$
to modal arithmetic. In particular, as suggested by Guaspari’s result,
$\mathrm {DP}$
to modal arithmetic. In particular, as suggested by Guaspari’s result,
![]() $\mathrm {MDP}$
and
$\mathrm {MDP}$
and
![]() $\mathrm {MEP}$
may be characterized by soundness with respect to some class of
$\mathrm {MEP}$
may be characterized by soundness with respect to some class of
![]() $\mathcal {L}_A(\Box )$
-formulas. For this reason, in the present paper, we introduce three new classes
$\mathcal {L}_A(\Box )$
-formulas. For this reason, in the present paper, we introduce three new classes
![]() $\mathrm {B}$
,
$\mathrm {B}$
,
![]() $\Delta (\mathrm {B})$
, and
$\Delta (\mathrm {B})$
, and
![]() $\Sigma (\mathrm {B})$
of
$\Sigma (\mathrm {B})$
of
![]() $\mathcal {L}_A(\Box )$
-formulas. Then, we prove that for any consistent r.e.
$\mathcal {L}_A(\Box )$
-formulas. Then, we prove that for any consistent r.e.
![]() $\mathcal {L}_A(\Box )$
-theory T extending
$\mathcal {L}_A(\Box )$
-theory T extending
![]() $\mathbf {PA}(\mathbf {K4})$
, T has
$\mathbf {PA}(\mathbf {K4})$
, T has
![]() $\mathrm {MDP}$
if and only if T is
$\mathrm {MDP}$
if and only if T is
![]() $\Sigma (\mathrm {B})$
-sound. We also provide a systematic analysis of the disjunction and the existence properties in modal arithmetic, including investigations of
$\Sigma (\mathrm {B})$
-sound. We also provide a systematic analysis of the disjunction and the existence properties in modal arithmetic, including investigations of
![]() $\mathrm {DP}$
and
$\mathrm {DP}$
and
![]() $\mathrm {EP}$
concerning these new classes of formulas.
$\mathrm {EP}$
concerning these new classes of formulas.

Fig. 1 Implications for consistent r.e. extensions T of
![]() $\mathbf {PA}(\mathbf {K4})$
with
$\mathbf {PA}(\mathbf {K4})$
with
![]() $T \nvdash \Box \bot $
.
$T \nvdash \Box \bot $
.
The present paper is organized as follows. In Section 2, we introduce several theories of modal arithmetic and show that each of them is a conservative extension of
![]() $\mathbf {PA}$
. In Section 3, we introduce three new classes
$\mathbf {PA}$
. In Section 3, we introduce three new classes
![]() $\mathrm {B}$
,
$\mathrm {B}$
,
![]() $\Delta (\mathrm {B})$
, and
$\Delta (\mathrm {B})$
, and
![]() $\Sigma (\mathrm {B})$
of
$\Sigma (\mathrm {B})$
of
![]() $\mathcal {L}_A(\Box )$
-formulas and show some basic properties of these classes. Section 4 is devoted to the study of
$\mathcal {L}_A(\Box )$
-formulas and show some basic properties of these classes. Section 4 is devoted to the study of
![]() $\mathrm {B}$
-
$\mathrm {B}$
-
![]() $\mathrm {DP}$
,
$\mathrm {DP}$
,
![]() $\Delta (\mathrm {B})$
-
$\Delta (\mathrm {B})$
-
![]() $\mathrm {DP}$
, and related properties. In Section 5, we study
$\mathrm {DP}$
, and related properties. In Section 5, we study
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {DP}$
and related properties. In particular, we prove that for any r.e. extension T of the theory
$\mathrm {DP}$
and related properties. In particular, we prove that for any r.e. extension T of the theory
![]() $\mathbf {PA}(\mathbf {K})$
, if
$\mathbf {PA}(\mathbf {K})$
, if
![]() $T \nvdash \Box \bot $
, then
$T \nvdash \Box \bot $
, then
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {DP}$
,
$\mathrm {DP}$
,
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {EP}$
, and
$\mathrm {EP}$
, and
![]() $\mathrm {B}$
-
$\mathrm {B}$
-
![]() $\mathrm {EP}$
are pairwise equivalent. From this result, the equivalence of
$\mathrm {EP}$
are pairwise equivalent. From this result, the equivalence of
![]() $\mathrm {MDP}$
and
$\mathrm {MDP}$
and
![]() $\mathrm {MEP}$
for any consistent r.e.
$\mathrm {MEP}$
for any consistent r.e.
![]() $\mathcal {L}_A(\Box )$
-theory extending
$\mathcal {L}_A(\Box )$
-theory extending
![]() $\mathbf {PA}(\mathbf {K4})$
is obtained. In Section 6, as generalizations of the notions of the soundness and the
$\mathbf {PA}(\mathbf {K4})$
is obtained. In Section 6, as generalizations of the notions of the soundness and the
![]() $\Sigma _1$
-soundness of
$\Sigma _1$
-soundness of
![]() $\mathcal {L}_A$
-theories, we introduce the notions of the
$\mathcal {L}_A$
-theories, we introduce the notions of the
![]() $\mathcal {L}_A(\Box )$
-soundness and the
$\mathcal {L}_A(\Box )$
-soundness and the
![]() $\Sigma (\mathrm {B})$
-soundness of
$\Sigma (\mathrm {B})$
-soundness of
![]() $\mathcal {L}_A(\Box )$
-theories. We study these notions precisely, and then, we prove that for any consistent r.e. extension T of
$\mathcal {L}_A(\Box )$
-theories. We study these notions precisely, and then, we prove that for any consistent r.e. extension T of
![]() $\mathbf {PA}(\mathbf {K4})$
, T has
$\mathbf {PA}(\mathbf {K4})$
, T has
![]() $\mathrm {MDP}$
if and only T is
$\mathrm {MDP}$
if and only T is
![]() $\Sigma (\mathrm {B})$
-sound. This is a modal arithmetical analogue of Guaspari’s theorem. Figure 1 summarizes our results obtained in Sections 4–6. We also show some non-implications between the properties:
$\Sigma (\mathrm {B})$
-sound. This is a modal arithmetical analogue of Guaspari’s theorem. Figure 1 summarizes our results obtained in Sections 4–6. We also show some non-implications between the properties:
![]() $\Sigma _1$
-soundness does not imply
$\Sigma _1$
-soundness does not imply
![]() $(\mathrm {B}, \Sigma _1)$
-
$(\mathrm {B}, \Sigma _1)$
-
![]() $\mathrm {DP}$
(Proposition 4.28),
$\mathrm {DP}$
(Proposition 4.28),
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {EP}$
does not imply
$\mathrm {EP}$
does not imply
![]() $\mathrm {MDP}$
(Proposition 6.65), and
$\mathrm {MDP}$
(Proposition 6.65), and
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {DC}$
does not imply
$\mathrm {DC}$
does not imply
![]() $\mathrm {B}$
-
$\mathrm {B}$
-
![]() $\mathrm {DP}$
(Proposition 6.66). Finally, in the last section, we list several unsolved problems.
$\mathrm {DP}$
(Proposition 6.66). Finally, in the last section, we list several unsolved problems.
2 Theories of modal arithmetic
We work within the framework of modal arithmetic. The language
![]() $\mathcal {L}_A(\Box )$
of modal arithmetic consists of logical connectives
$\mathcal {L}_A(\Box )$
of modal arithmetic consists of logical connectives
![]() $\bot , \land , \lor , \to , \neg $
, quantifiers
$\bot , \land , \lor , \to , \neg $
, quantifiers
![]() $\forall , \exists $
, elements of the language
$\forall , \exists $
, elements of the language
![]() $\mathcal {L}_A = \{0, S, +, \times , \leq , =\}$
of first-order arithmetic, and modal operator
$\mathcal {L}_A = \{0, S, +, \times , \leq , =\}$
of first-order arithmetic, and modal operator
![]() $\Box $
. The formulas
$\Box $
. The formulas
![]() $\varphi \leftrightarrow \psi $
and
$\varphi \leftrightarrow \psi $
and
![]() $\Diamond \varphi $
are abbreviations for
$\Diamond \varphi $
are abbreviations for
![]() $(\varphi \to \psi ) \land (\psi \to \varphi )$
and
$(\varphi \to \psi ) \land (\psi \to \varphi )$
and
![]() $\neg \Box \neg \varphi $
, respectively. A set of sentences is called a theory. In the present paper, we always assume that the inference rules of every
$\neg \Box \neg \varphi $
, respectively. A set of sentences is called a theory. In the present paper, we always assume that the inference rules of every
![]() $\mathcal {L}_A(\Box )$
-theory are modus ponens (MP)
$\mathcal {L}_A(\Box )$
-theory are modus ponens (MP)
![]() $\dfrac {\varphi \to \psi \quad \varphi }{\psi }$
, generalization (Gen)
$\dfrac {\varphi \to \psi \quad \varphi }{\psi }$
, generalization (Gen)
![]() $\dfrac {\varphi }{\forall x \varphi }$
, and necessitation (Nec)
$\dfrac {\varphi }{\forall x \varphi }$
, and necessitation (Nec)
![]() $\dfrac {\varphi }{\Box \varphi }$
. Since we will study modal arithmetic from a broader perspective than just
$\dfrac {\varphi }{\Box \varphi }$
. Since we will study modal arithmetic from a broader perspective than just
![]() $\mathbf {EA}$
, we also deal with
$\mathbf {EA}$
, we also deal with
![]() $\mathcal {L}_A(\Box )$
-theories obtained by adding normal modal propositional logics other than
$\mathcal {L}_A(\Box )$
-theories obtained by adding normal modal propositional logics other than
![]() $\mathbf {S4}$
into
$\mathbf {S4}$
into
![]() $\mathbf {PA}$
. Let
$\mathbf {PA}$
. Let
![]() $\mathbf {PA}_{\Box }$
be the
$\mathbf {PA}_{\Box }$
be the
![]() $\mathcal {L}_A(\Box )$
-theory obtained by adding the logical axioms of first-order logic for
$\mathcal {L}_A(\Box )$
-theory obtained by adding the logical axioms of first-order logic for
![]() $\mathcal {L}_A(\Box )$
-formulas and the induction axioms for
$\mathcal {L}_A(\Box )$
-formulas and the induction axioms for
![]() $\mathcal {L}_A(\Box )$
-formulas into
$\mathcal {L}_A(\Box )$
-formulas into
![]() $\mathbf {PA}$
. Notice that the value of each
$\mathbf {PA}$
. Notice that the value of each
![]() $\mathcal {L}_A$
-term
$\mathcal {L}_A$
-term
![]() $t(\vec {x})$
can be effectively computed from the input
$t(\vec {x})$
can be effectively computed from the input
![]() $\vec {x}$
, and thus universal instantiation
$\vec {x}$
, and thus universal instantiation
![]() $\forall x \varphi (x) \to \varphi (t)$
(where
$\forall x \varphi (x) \to \varphi (t)$
(where
![]() $t$
is an
$t$
is an
![]() $\mathcal {L}_A$
-term substitutable for
$\mathcal {L}_A$
-term substitutable for
![]() $x$
in
$x$
in
![]() $\varphi $
), which is problematic in modal predicate logic, is not a problem in our framework. As in [Reference Došen3, Reference Friedman and Sheard6, Reference Reinhardt19, Reference Shapiro21], we adopt universal instantiation as an axiom scheme of
$\varphi $
), which is problematic in modal predicate logic, is not a problem in our framework. As in [Reference Došen3, Reference Friedman and Sheard6, Reference Reinhardt19, Reference Shapiro21], we adopt universal instantiation as an axiom scheme of
![]() $\mathbf {PA}_{\Box }$
. Of course, this is not the case in general framework (see [Reference Shapiro21, sec. 7]).
$\mathbf {PA}_{\Box }$
. Of course, this is not the case in general framework (see [Reference Shapiro21, sec. 7]).
For each normal modal propositional logic L, let
![]() $\mathbf {PA}(L)$
denote the
$\mathbf {PA}(L)$
denote the
![]() $\mathcal {L}_A(\Box )$
-theory obtained by adding universal closures of formulas corresponding to modal axioms of L into
$\mathcal {L}_A(\Box )$
-theory obtained by adding universal closures of formulas corresponding to modal axioms of L into
![]() $\mathbf {PA}_{\Box }$
. We deal with the following
$\mathbf {PA}_{\Box }$
. We deal with the following
![]() $\mathcal {L}_A(\Box )$
-theories.
$\mathcal {L}_A(\Box )$
-theories.
-
•
 $\mathbf {PA}(\mathbf {K}) = \mathbf {PA}_{\Box } + \{\forall \vec {x}(\Box (\varphi \to \psi ) \to (\Box \varphi \to \Box \psi )) \mid \varphi , \psi $
are
$\mathbf {PA}(\mathbf {K}) = \mathbf {PA}_{\Box } + \{\forall \vec {x}(\Box (\varphi \to \psi ) \to (\Box \varphi \to \Box \psi )) \mid \varphi , \psi $
are
 $\mathcal {L}_A(\Box )$
-formulas
$\mathcal {L}_A(\Box )$
-formulas
 $\}$
;
$\}$
; -
•
 $\mathbf {PA}(\mathbf {K4}) = \mathbf {PA}(\mathbf {K}) + \{\forall \vec {x}(\Box \varphi \to \Box \Box \varphi ) \mid \varphi $
is an
$\mathbf {PA}(\mathbf {K4}) = \mathbf {PA}(\mathbf {K}) + \{\forall \vec {x}(\Box \varphi \to \Box \Box \varphi ) \mid \varphi $
is an
 $\mathcal {L}_A(\Box )$
-formula
$\mathcal {L}_A(\Box )$
-formula
 $\}$
;
$\}$
; -
•
 $\mathbf {PA}(\mathbf {KT}) = \mathbf {PA}(\mathbf {K}) + \{\forall \vec {x}(\Box \varphi \to \varphi ) \mid \varphi $
is an
$\mathbf {PA}(\mathbf {KT}) = \mathbf {PA}(\mathbf {K}) + \{\forall \vec {x}(\Box \varphi \to \varphi ) \mid \varphi $
is an
 $\mathcal {L}_A(\Box )$
-formula
$\mathcal {L}_A(\Box )$
-formula
 $\}$
;
$\}$
; -
•
 $\mathbf {PA}(\mathbf {S4}) = \mathbf {EA} = \mathbf {PA}(\mathbf {KT}) + \{\forall \vec {x}(\Box \varphi \to \Box \Box \varphi ) \mid \varphi $
is an
$\mathbf {PA}(\mathbf {S4}) = \mathbf {EA} = \mathbf {PA}(\mathbf {KT}) + \{\forall \vec {x}(\Box \varphi \to \Box \Box \varphi ) \mid \varphi $
is an
 $\mathcal {L}_A(\Box )$
-formula
$\mathcal {L}_A(\Box )$
-formula
 $\}$
;
$\}$
; -
•
 $\mathbf {PA}(\mathbf {S5}) = \mathbf {PA}(\mathbf {S4}) + \{\forall \vec {x}(\Diamond \varphi \to \Box \Diamond \varphi ) \mid \varphi $
is an
$\mathbf {PA}(\mathbf {S5}) = \mathbf {PA}(\mathbf {S4}) + \{\forall \vec {x}(\Diamond \varphi \to \Box \Diamond \varphi ) \mid \varphi $
is an
 $\mathcal {L}_A(\Box )$
-formula
$\mathcal {L}_A(\Box )$
-formula
 $\}$
;
$\}$
; -
•
 $\mathbf {PA}(\mathbf {Triv}) = \mathbf {PA}(\mathbf {K}) + \{\forall \vec {x}(\Box \varphi \leftrightarrow \varphi ) \mid \varphi $
is an
$\mathbf {PA}(\mathbf {Triv}) = \mathbf {PA}(\mathbf {K}) + \{\forall \vec {x}(\Box \varphi \leftrightarrow \varphi ) \mid \varphi $
is an
 $\mathcal {L}_A(\Box )$
-formula
$\mathcal {L}_A(\Box )$
-formula
 $\}$
;
$\}$
; -
•
 $\mathbf {PA}(\mathbf {GL}) = \mathbf {PA}(\mathbf {K4}) + \{\forall \vec {x}(\Box (\Box \varphi \to \varphi ) \to \Box \varphi ) \mid \varphi $
is an
$\mathbf {PA}(\mathbf {GL}) = \mathbf {PA}(\mathbf {K4}) + \{\forall \vec {x}(\Box (\Box \varphi \to \varphi ) \to \Box \varphi ) \mid \varphi $
is an
 $\mathcal {L}_A(\Box )$
-formula
$\mathcal {L}_A(\Box )$
-formula
 $\}$
;
$\}$
; -
•
 $\mathbf {PA}(\mathbf {Verum}) = \mathbf {PA}(\mathbf {K}) + \{\Box \bot \}$
.
$\mathbf {PA}(\mathbf {Verum}) = \mathbf {PA}(\mathbf {K}) + \{\Box \bot \}$
.
Interestingly, Došen [Reference Došen3, Lemma 7] proved that
![]() $\mathbf {PA}(\mathbf {S5})$
and
$\mathbf {PA}(\mathbf {S5})$
and
![]() $\mathbf {PA}(\mathbf {Triv})$
are deductively equivalent.
$\mathbf {PA}(\mathbf {Triv})$
are deductively equivalent.
Here we discuss the principle
![]() $x = y \to (\varphi (x) \to \varphi (y))$
of identity. Our system has this principle only for atomic formulas
$x = y \to (\varphi (x) \to \varphi (y))$
of identity. Our system has this principle only for atomic formulas
![]() $\varphi (x)$
as identity axioms as in the case of classical first-order logic. On the other hand, this principle for all
$\varphi (x)$
as identity axioms as in the case of classical first-order logic. On the other hand, this principle for all
![]() $\mathcal {L}_A(\Box )$
-formulas is not generally valid in our framework because our language has the symbol
$\mathcal {L}_A(\Box )$
-formulas is not generally valid in our framework because our language has the symbol
![]() $\Box $
. Shapiro [Reference Shapiro21] states that the following proposition holds for
$\Box $
. Shapiro [Reference Shapiro21] states that the following proposition holds for
![]() $\mathbf {PA}(\mathbf {S4})$
.
$\mathbf {PA}(\mathbf {S4})$
.
Proposition 2.1.
-
1.
 $\mathbf {PA}(\mathbf {K}) \vdash x = y \to \Box x = y$
.
$\mathbf {PA}(\mathbf {K}) \vdash x = y \to \Box x = y$
. -
2. For any
 $\mathcal {L}_A(\Box )$
-formula
$\mathcal {L}_A(\Box )$
-formula
 $\varphi (x)$
,
$\varphi (x)$
,
 $\mathbf {PA}(\mathbf {K}) \vdash x = y \to (\varphi (x) \to \varphi (y))$
.
$\mathbf {PA}(\mathbf {K}) \vdash x = y \to (\varphi (x) \to \varphi (y))$
.
Proof. 1. Let
![]() $\varphi (x, y)$
be the formula
$\varphi (x, y)$
be the formula
![]() $x = y \to \Box x = y$
. Firstly, we prove
$x = y \to \Box x = y$
. Firstly, we prove
![]() $\mathbf {PA}_{\Box } \vdash \forall y \varphi (0, y)$
. Since
$\mathbf {PA}_{\Box } \vdash \forall y \varphi (0, y)$
. Since
![]() $\mathbf {PA} \vdash 0 = 0$
, we have
$\mathbf {PA} \vdash 0 = 0$
, we have
![]() $\mathbf {PA}_{\Box } \vdash \Box 0 = 0$
, and hence
$\mathbf {PA}_{\Box } \vdash \Box 0 = 0$
, and hence
![]() $\mathbf {PA}_{\Box } \vdash \varphi (0, 0)$
. Since
$\mathbf {PA}_{\Box } \vdash \varphi (0, 0)$
. Since
![]() $\mathbf {PA} \vdash 0 \neq S(y)$
, we also have
$\mathbf {PA} \vdash 0 \neq S(y)$
, we also have
![]() $\mathbf {PA}_{\Box } \vdash \varphi (0, S(y))$
, and thus
$\mathbf {PA}_{\Box } \vdash \varphi (0, S(y))$
, and thus
![]() $\mathbf {PA}_{\Box } \vdash \forall y(\varphi (0, y) \to \varphi (0, S(y)))$
. By the induction axiom for
$\mathbf {PA}_{\Box } \vdash \forall y(\varphi (0, y) \to \varphi (0, S(y)))$
. By the induction axiom for
![]() $\varphi (0, y)$
, we obtain
$\varphi (0, y)$
, we obtain
![]() $\mathbf {PA}_{\Box } \vdash \forall y \varphi (0, y)$
.
$\mathbf {PA}_{\Box } \vdash \forall y \varphi (0, y)$
.
Secondly, we prove
![]() $\mathbf {PA}(\mathbf {K}) \vdash \forall y \varphi (x, y) \to \forall y \varphi (S(x), y)$
. Since
$\mathbf {PA}(\mathbf {K}) \vdash \forall y \varphi (x, y) \to \forall y \varphi (S(x), y)$
. Since
![]() $\mathbf {PA} \vdash S(x) \neq 0$
, we have
$\mathbf {PA} \vdash S(x) \neq 0$
, we have
![]() $\mathbf {PA}_{\Box } \vdash \varphi (S(x), 0)$
. It follows from
$\mathbf {PA}_{\Box } \vdash \varphi (S(x), 0)$
. It follows from
![]() $\mathbf {PA} \vdash S(x) = S(y) \to x = y$
that
$\mathbf {PA} \vdash S(x) = S(y) \to x = y$
that
![]() $\mathbf {PA}_{\Box } \vdash \varphi (x, y) \land S(x) = S(y) \to \Box x = y$
. Since
$\mathbf {PA}_{\Box } \vdash \varphi (x, y) \land S(x) = S(y) \to \Box x = y$
. Since
![]() $\mathbf {PA} \vdash x = y \to S(x) = S(y)$
, we have
$\mathbf {PA} \vdash x = y \to S(x) = S(y)$
, we have
![]() $\mathbf {PA}(\mathbf {K}) \vdash \Box x = y \to \Box S(x) = S(y)$
. Thus, we get
$\mathbf {PA}(\mathbf {K}) \vdash \Box x = y \to \Box S(x) = S(y)$
. Thus, we get
This means
![]() $\mathbf {PA}(\mathbf {K}) \vdash \varphi (x, y) \to \varphi (S(x), S(y))$
. By the universal instantiation, we have
$\mathbf {PA}(\mathbf {K}) \vdash \varphi (x, y) \to \varphi (S(x), S(y))$
. By the universal instantiation, we have
![]() $\mathbf {PA}(\mathbf {K}) \vdash \forall y \varphi (x, y) \to \varphi (S(x), S(y))$
, and hence
$\mathbf {PA}(\mathbf {K}) \vdash \forall y \varphi (x, y) \to \varphi (S(x), S(y))$
, and hence
From this with
![]() $\mathbf {PA}_{\Box } \vdash \varphi (S(x), 0)$
, we obtain
$\mathbf {PA}_{\Box } \vdash \varphi (S(x), 0)$
, we obtain
![]() $\mathbf {PA}(\mathbf {K}) \vdash \forall y \varphi (x, y) \to \forall y \varphi (S(x), y)$
by the induction axiom for
$\mathbf {PA}(\mathbf {K}) \vdash \forall y \varphi (x, y) \to \forall y \varphi (S(x), y)$
by the induction axiom for
![]() $\varphi (S(x), y)$
.
$\varphi (S(x), y)$
.
Finally, by the induction axiom for
![]() $\forall y \varphi (x, y)$
, we conclude
$\forall y \varphi (x, y)$
, we conclude
![]() $\mathbf {PA}(\mathbf {K}) \vdash \forall x \forall y \varphi (x, y)$
.
$\mathbf {PA}(\mathbf {K}) \vdash \forall x \forall y \varphi (x, y)$
.
2. This is proved by induction on the construction of
![]() $\varphi (x)$
. We only prove the case that
$\varphi (x)$
. We only prove the case that
![]() $\varphi (x)$
is of the form
$\varphi (x)$
is of the form
![]() $\Box \psi (x)$
and the statement holds for
$\Box \psi (x)$
and the statement holds for
![]() $\psi (x)$
. By the induction hypothesis,
$\psi (x)$
. By the induction hypothesis,
![]() $\mathbf {PA}(\mathbf {K}) \vdash x = y \to (\psi (x) \to \psi (y))$
. Then,
$\mathbf {PA}(\mathbf {K}) \vdash x = y \to (\psi (x) \to \psi (y))$
. Then,
![]() $\mathbf {PA}(\mathbf {K})$
proves
$\mathbf {PA}(\mathbf {K})$
proves
![]() $\Box x = y \to (\Box \psi (x) \to \Box \psi (y))$
. By combining this with Clause 1, we conclude
$\Box x = y \to (\Box \psi (x) \to \Box \psi (y))$
. By combining this with Clause 1, we conclude
![]() $\mathbf {PA}(\mathbf {K}) \vdash x = y \to (\Box \psi (x) \to \Box \psi (y))$
.
$\mathbf {PA}(\mathbf {K}) \vdash x = y \to (\Box \psi (x) \to \Box \psi (y))$
.
We say that a theory T is a subtheory of a theory U,
![]() $U \vdash T$
, if every axiom of T is provable in U. Makinson’s theorem [Reference Makinson17] states that every consistent normal modal propositional logic L is a sublogic of
$U \vdash T$
, if every axiom of T is provable in U. Makinson’s theorem [Reference Makinson17] states that every consistent normal modal propositional logic L is a sublogic of
![]() $\mathbf {Triv}$
or
$\mathbf {Triv}$
or
![]() $\mathbf {Verum}$
(see also [Reference Hughes and Cresswell12]). Hence, every
$\mathbf {Verum}$
(see also [Reference Hughes and Cresswell12]). Hence, every
![]() $\mathcal {L}_A(\Box )$
-theory of the form
$\mathcal {L}_A(\Box )$
-theory of the form
![]() $\mathbf {PA}(L)$
for some consistent normal propositional modal logic L is a subtheory of
$\mathbf {PA}(L)$
for some consistent normal propositional modal logic L is a subtheory of
![]() $\mathbf {PA}(\mathbf {Triv})$
or
$\mathbf {PA}(\mathbf {Triv})$
or
![]() $\mathbf {PA}(\mathbf {Verum})$
. We prove that every such logic is a conservative extension of
$\mathbf {PA}(\mathbf {Verum})$
. We prove that every such logic is a conservative extension of
![]() $\mathbf {PA}$
.
$\mathbf {PA}$
.
First, we prove that
![]() $\mathbf {PA}(\mathbf {Triv})$
is a conservative extension of
$\mathbf {PA}(\mathbf {Triv})$
is a conservative extension of
![]() $\mathbf {PA}$
. In order to prove this, we introduce a translation
$\mathbf {PA}$
. In order to prove this, we introduce a translation
![]() $\alpha $
of
$\alpha $
of
![]() $\mathcal {L}_A(\Box )$
-formulas into
$\mathcal {L}_A(\Box )$
-formulas into
![]() $\mathcal {L}_A$
-formulas.
$\mathcal {L}_A$
-formulas.
Definition 2.2 (
 $\alpha $
-translation)
$\alpha $
-translation)
We define a translation
![]() $\alpha $
of
$\alpha $
of
![]() $\mathcal {L}_A(\Box )$
-formulas into
$\mathcal {L}_A(\Box )$
-formulas into
![]() $\mathcal {L}_A$
-formulas inductively as follows:
$\mathcal {L}_A$
-formulas inductively as follows:
-
1. If
 $\varphi $
is an
$\varphi $
is an
 $\mathcal {L}_A$
-formula, then
$\mathcal {L}_A$
-formula, then
 $\alpha (\varphi ) : \equiv \varphi $
.
$\alpha (\varphi ) : \equiv \varphi $
. -
2.
 $\alpha $
preserves logical connectives and quantifiers.
$\alpha $
preserves logical connectives and quantifiers. -
3.
 $\alpha (\Box \varphi ) : \equiv \alpha (\varphi )$
.
$\alpha (\Box \varphi ) : \equiv \alpha (\varphi )$
.
It is obvious that for any
![]() $\mathcal {L}_A(\Box )$
-formula
$\mathcal {L}_A(\Box )$
-formula
![]() $\varphi $
,
$\varphi $
,
![]() $\mathbf {PA}(\mathbf {Triv}) \vdash \varphi \leftrightarrow \alpha (\varphi )$
. Moreover:
$\mathbf {PA}(\mathbf {Triv}) \vdash \varphi \leftrightarrow \alpha (\varphi )$
. Moreover:
Proposition 2.3. For any
![]() $\mathcal {L}_A(\Box )$
-formula
$\mathcal {L}_A(\Box )$
-formula
![]() $\varphi $
, if
$\varphi $
, if
![]() $\mathbf {PA}(\mathbf {Triv}) \vdash \varphi $
, then
$\mathbf {PA}(\mathbf {Triv}) \vdash \varphi $
, then
![]() $\mathbf {PA} \vdash \alpha (\varphi )$
.
$\mathbf {PA} \vdash \alpha (\varphi )$
.
Proof. We prove the proposition by induction on the length of proofs of
![]() $\varphi $
in
$\varphi $
in
![]() $\mathbf {PA}(\mathbf {Triv})$
.
$\mathbf {PA}(\mathbf {Triv})$
.
-
• If
 $\varphi $
is an axiom of
$\varphi $
is an axiom of
 $\mathbf {PA}$
, then
$\mathbf {PA}$
, then
 $\alpha (\varphi ) \equiv \varphi $
and
$\alpha (\varphi ) \equiv \varphi $
and
 $\mathbf {PA} \vdash \alpha (\varphi )$
.
$\mathbf {PA} \vdash \alpha (\varphi )$
. -
• If
 $\varphi $
is a logical axiom, then so is
$\varphi $
is a logical axiom, then so is
 $\alpha (\varphi )$
, and it is
$\alpha (\varphi )$
, and it is
 $\mathbf {PA}$
-provable.
$\mathbf {PA}$
-provable. -
• If
 $\varphi $
is an induction axiom in the language
$\varphi $
is an induction axiom in the language
 $\mathcal {L}_A(\Box )$
, then
$\mathcal {L}_A(\Box )$
, then
 $\alpha (\varphi )$
is also an induction axiom in
$\alpha (\varphi )$
is also an induction axiom in
 $\mathcal {L}_A$
, and so
$\mathcal {L}_A$
, and so
 $\mathbf {PA} \vdash \alpha (\varphi )$
.
$\mathbf {PA} \vdash \alpha (\varphi )$
. -
• If
 $\varphi $
is
$\varphi $
is
 $\forall \vec {x}(\Box (\psi \to \sigma ) \to (\Box \psi \to \Box \sigma ))$
, then
$\forall \vec {x}(\Box (\psi \to \sigma ) \to (\Box \psi \to \Box \sigma ))$
, then
 $\alpha (\varphi )$
is the
$\alpha (\varphi )$
is the
 $\mathbf {PA}$
-provable sentence
$\mathbf {PA}$
-provable sentence
 $\forall \vec {x} \bigl ((\alpha (\psi ) \to \alpha (\sigma )) \to (\alpha (\psi ) \to \alpha (\sigma )) \bigr )$
.
$\forall \vec {x} \bigl ((\alpha (\psi ) \to \alpha (\sigma )) \to (\alpha (\psi ) \to \alpha (\sigma )) \bigr )$
. -
• If
 $\varphi $
is
$\varphi $
is
 $\forall \vec {x} (\psi \leftrightarrow \Box \psi )$
, then
$\forall \vec {x} (\psi \leftrightarrow \Box \psi )$
, then
 $\alpha (\varphi )$
is
$\alpha (\varphi )$
is
 $\forall \vec {x}(\alpha (\psi ) \leftrightarrow \alpha (\psi ))$
. This is provable in
$\forall \vec {x}(\alpha (\psi ) \leftrightarrow \alpha (\psi ))$
. This is provable in
 $\mathbf {PA}$
.
$\mathbf {PA}$
. -
• If
 $\varphi $
is derived from
$\varphi $
is derived from
 $\psi $
and
$\psi $
and
 $\psi \to \varphi $
by MP, then by the induction hypothesis,
$\psi \to \varphi $
by MP, then by the induction hypothesis,
 $\mathbf {PA} \vdash \alpha (\psi )$
and
$\mathbf {PA} \vdash \alpha (\psi )$
and
 $\mathbf {PA} \vdash \alpha (\psi ) \to \alpha (\varphi )$
, and hence
$\mathbf {PA} \vdash \alpha (\psi ) \to \alpha (\varphi )$
, and hence
 $\mathbf {PA} \vdash \alpha (\varphi )$
.
$\mathbf {PA} \vdash \alpha (\varphi )$
. -
• If
 $\varphi $
is derived from
$\varphi $
is derived from
 $\psi (x)$
by Gen, then
$\psi (x)$
by Gen, then
 $\varphi \equiv \forall x \psi (x)$
. By the induction hypothesis,
$\varphi \equiv \forall x \psi (x)$
. By the induction hypothesis,
 $\mathbf {PA} \vdash \alpha (\psi (x))$
and hence
$\mathbf {PA} \vdash \alpha (\psi (x))$
and hence
 $\mathbf {PA} \vdash \forall x \alpha (\psi (x))$
. Therefore,
$\mathbf {PA} \vdash \forall x \alpha (\psi (x))$
. Therefore,
 $\mathbf {PA} \vdash \alpha (\varphi )$
.
$\mathbf {PA} \vdash \alpha (\varphi )$
. -
• If
 $\varphi $
is derived from
$\varphi $
is derived from
 $\psi $
by Nec, then
$\psi $
by Nec, then
 $\varphi \equiv \Box \psi $
. By the induction hypothesis,
$\varphi \equiv \Box \psi $
. By the induction hypothesis,
 $\mathbf {PA} \vdash \alpha (\psi )$
. Since
$\mathbf {PA} \vdash \alpha (\psi )$
. Since
 $\alpha (\varphi ) \equiv \alpha (\psi )$
, we have
$\alpha (\varphi ) \equiv \alpha (\psi )$
, we have
 $\mathbf {PA} \vdash \alpha (\varphi )$
.
$\mathbf {PA} \vdash \alpha (\varphi )$
.
Let
![]() $\mathbb {N}$
be the standard model of arithmetic in the language
$\mathbb {N}$
be the standard model of arithmetic in the language
![]() $\mathcal {L}_A$
. We say that an
$\mathcal {L}_A$
. We say that an
![]() $\mathcal {L}_A(\Box )$
-theory T is
$\mathcal {L}_A(\Box )$
-theory T is
![]() $\mathcal {L}_A$
-sound if for any
$\mathcal {L}_A$
-sound if for any
![]() $\mathcal {L}_A$
-sentence
$\mathcal {L}_A$
-sentence
![]() $\varphi $
,
$\varphi $
,
![]() $\mathbb {N} \models \varphi $
whenever
$\mathbb {N} \models \varphi $
whenever
![]() $T \vdash \varphi $
.
$T \vdash \varphi $
.
Corollary 2.4.
![]() $\mathbf {PA}(\mathbf {Triv})$
is a conservative extension of
$\mathbf {PA}(\mathbf {Triv})$
is a conservative extension of
![]() $\mathbf {PA}$
. In particular,
$\mathbf {PA}$
. In particular,
![]() $\mathbf {PA}(\mathbf {Triv})$
is
$\mathbf {PA}(\mathbf {Triv})$
is
![]() $\mathcal {L}_A$
-sound.
$\mathcal {L}_A$
-sound.
Proof. Let
![]() $\varphi $
be any
$\varphi $
be any
![]() $\mathcal {L}_A$
-sentence such that
$\mathcal {L}_A$
-sentence such that
![]() $\mathbf {PA}(\mathbf {Triv}) \vdash \varphi $
. By Proposition 2.3,
$\mathbf {PA}(\mathbf {Triv}) \vdash \varphi $
. By Proposition 2.3,
![]() $\mathbf {PA} \vdash \alpha (\varphi )$
. Since
$\mathbf {PA} \vdash \alpha (\varphi )$
. Since
![]() $\alpha (\varphi ) \equiv \varphi $
,
$\alpha (\varphi ) \equiv \varphi $
,
![]() $\mathbf {PA} \vdash \varphi $
. Furthermore, by the
$\mathbf {PA} \vdash \varphi $
. Furthermore, by the
![]() $\mathcal {L}_A$
-soundness of
$\mathcal {L}_A$
-soundness of
![]() $\mathbf {PA}$
,
$\mathbf {PA}$
,
![]() $\mathbf {PA}(\mathbf {Triv})$
is also
$\mathbf {PA}(\mathbf {Triv})$
is also
![]() $\mathcal {L}_A$
-sound.
$\mathcal {L}_A$
-sound.
Next, we prove that
![]() $\mathbf {PA}(\mathbf {Verum})$
is a conservative extension of
$\mathbf {PA}(\mathbf {Verum})$
is a conservative extension of
![]() $\mathbf {PA}$
. We also introduce another translation
$\mathbf {PA}$
. We also introduce another translation
![]() $\beta $
.
$\beta $
.
Definition 2.5 (
 $\beta $
-translation)
$\beta $
-translation)
We define a translation
![]() $\beta $
of
$\beta $
of
![]() $\mathcal {L}_A(\Box )$
-formulas into
$\mathcal {L}_A(\Box )$
-formulas into
![]() $\mathcal {L}_A$
-formulas inductively as follows:
$\mathcal {L}_A$
-formulas inductively as follows:
-
1. If
 $\varphi $
is an
$\varphi $
is an
 $\mathcal {L}_A$
-formula, then
$\mathcal {L}_A$
-formula, then
 $\beta (\varphi ) : \equiv \varphi $
.
$\beta (\varphi ) : \equiv \varphi $
. -
2.
 $\beta $
preserves logical connectives and quantifiers.
$\beta $
preserves logical connectives and quantifiers. -
3.
 $\beta (\Box \varphi ) : \equiv 0=0$
.
$\beta (\Box \varphi ) : \equiv 0=0$
.
As in the case of
![]() $\alpha $
, for any
$\alpha $
, for any
![]() $\mathcal {L}_A(\Box )$
-formula
$\mathcal {L}_A(\Box )$
-formula
![]() $\varphi $
,
$\varphi $
,
![]() $\mathbf {PA}(\mathbf {Verum}) \vdash \varphi \leftrightarrow \beta (\varphi )$
. Moreover:
$\mathbf {PA}(\mathbf {Verum}) \vdash \varphi \leftrightarrow \beta (\varphi )$
. Moreover:
Proposition 2.6. For any
![]() $\mathcal {L}_A(\Box )$
-formula
$\mathcal {L}_A(\Box )$
-formula
![]() $\varphi $
, if
$\varphi $
, if
![]() $\mathbf {PA}(\mathbf {Verum}) \vdash \varphi $
, then
$\mathbf {PA}(\mathbf {Verum}) \vdash \varphi $
, then
![]() $\mathbf {PA} \vdash \beta (\varphi )$
.
$\mathbf {PA} \vdash \beta (\varphi )$
.
Proof. As in the proof of Proposition 2.3, this proposition is proved by induction on the length of proofs of
![]() $\varphi $
in
$\varphi $
in
![]() $\mathbf {PA}(\mathbf {Verum})$
. We only give proofs of the following three cases:
$\mathbf {PA}(\mathbf {Verum})$
. We only give proofs of the following three cases:
-
• If
 $\varphi $
is
$\varphi $
is
 $\forall \vec {x}(\Box (\psi \to \sigma ) \to (\Box \psi \to \Box \sigma ))$
, then
$\forall \vec {x}(\Box (\psi \to \sigma ) \to (\Box \psi \to \Box \sigma ))$
, then
 $\beta (\varphi )$
is the
$\beta (\varphi )$
is the
 $\mathbf {PA}$
-provable sentence
$\mathbf {PA}$
-provable sentence
 $\forall \vec {x} (0=0 \to (0=0 \to 0=0))$
.
$\forall \vec {x} (0=0 \to (0=0 \to 0=0))$
. -
• If
 $\varphi $
is
$\varphi $
is
 $\Box \bot $
, then
$\Box \bot $
, then
 $\beta (\varphi )$
is the
$\beta (\varphi )$
is the
 $\mathbf {PA}$
-provable sentence
$\mathbf {PA}$
-provable sentence
 $0=0$
.
$0=0$
. -
• If
 $\varphi $
is derived from
$\varphi $
is derived from
 $\psi $
by Nec, then
$\psi $
by Nec, then
 $\varphi \equiv \Box \psi $
. Since
$\varphi \equiv \Box \psi $
. Since
 $\beta (\varphi ) \equiv 0=0$
, this is
$\beta (\varphi ) \equiv 0=0$
, this is
 $\mathbf {PA}$
-provable.
$\mathbf {PA}$
-provable.
Corollary 2.7.
![]() $\mathbf {PA}(\mathbf {Verum})$
is a conservative extension of
$\mathbf {PA}(\mathbf {Verum})$
is a conservative extension of
![]() $\mathbf {PA}$
. In particular,
$\mathbf {PA}$
. In particular,
![]() $\mathbf {PA}(\mathbf {Verum})$
is
$\mathbf {PA}(\mathbf {Verum})$
is
![]() $\mathcal {L}_A$
-sound.
$\mathcal {L}_A$
-sound.
We close this section by showing that the notion of
![]() $\Sigma _1$
formulas has a high affinity with modal arithmetic. The following theorem is proved by applying a schematic proof of formalized
$\Sigma _1$
formulas has a high affinity with modal arithmetic. The following theorem is proved by applying a schematic proof of formalized
![]() $\Sigma _1$
-completeness theorem (see [Reference Buchholz2, Reference Kurahashi16, Reference Rautenberg18]). This is also implicitly stated in [Reference Friedman and Sheard6].
$\Sigma _1$
-completeness theorem (see [Reference Buchholz2, Reference Kurahashi16, Reference Rautenberg18]). This is also implicitly stated in [Reference Friedman and Sheard6].
Theorem 2.8 (Formalized
 $\Sigma _1$
-completeness theorem)
$\Sigma _1$
-completeness theorem)
For any
![]() $\Sigma _1$
formula
$\Sigma _1$
formula
![]() $\varphi $
, we have
$\varphi $
, we have
![]() $\mathbf {PA}(\mathbf {K}) \vdash \varphi \to \Box \varphi $
.
$\mathbf {PA}(\mathbf {K}) \vdash \varphi \to \Box \varphi $
.
Proof. Before proving the theorem, we show that for any
![]() $\Sigma _1$
formula
$\Sigma _1$
formula
![]() $\psi $
, there exists a
$\psi $
, there exists a
![]() $\Sigma _1$
formula
$\Sigma _1$
formula
![]() $\psi '$
such that
$\psi '$
such that
![]() $\mathbf {PA} \vdash \psi \leftrightarrow \psi '$
,
$\mathbf {PA} \vdash \psi \leftrightarrow \psi '$
,
![]() $\psi '$
does not contain the connectives
$\psi '$
does not contain the connectives
![]() $\neg $
and
$\neg $
and
![]() $\to $
, and every atomic formula contained in
$\to $
, and every atomic formula contained in
![]() $\psi '$
is of the form
$\psi '$
is of the form
![]() $t_1 = t_2$
for some
$t_1 = t_2$
for some
![]() $\mathcal {L}_A$
-terms
$\mathcal {L}_A$
-terms
![]() $t_1$
and
$t_1$
and
![]() $t_2$
. First, we easily find a
$t_2$
. First, we easily find a
![]() $\Sigma _1$
formula
$\Sigma _1$
formula
![]() $\psi _0$
without the connective
$\psi _0$
without the connective
![]() $\to $
such that
$\to $
such that
![]() $\psi _0$
is logically equivalent to
$\psi _0$
is logically equivalent to
![]() $\psi $
and every negation symbol
$\psi $
and every negation symbol
![]() $\neg $
in
$\neg $
in
![]() $\psi _0$
is applied to an atomic formula. Then, by replacing every negated atomic formula
$\psi _0$
is applied to an atomic formula. Then, by replacing every negated atomic formula
![]() $\neg (t_1 = t_2)$
or
$\neg (t_1 = t_2)$
or
![]() $\neg (t_1 < t_2)$
of
$\neg (t_1 < t_2)$
of
![]() $\psi_0$
by
$\psi_0$
by
![]() $t_1 < t_2 \lor t_2 < t_1$
or
$t_1 < t_2 \lor t_2 < t_1$
or
![]() $t_1 = t_2 \lor t_2 < t_1$
respectively, we obtain a
$t_1 = t_2 \lor t_2 < t_1$
respectively, we obtain a
![]() $\mathbf {PA}$
-equivalent
$\mathbf {PA}$
-equivalent
![]() $\Sigma _1$
formula
$\Sigma _1$
formula
![]() $\psi _1$
without having
$\psi _1$
without having
![]() $\neg $
. Finally, by replacing every atomic formula
$\neg $
. Finally, by replacing every atomic formula
![]() $t_1 < t_2$
of
$t_1 < t_2$
of
![]() $\psi _1$
by
$\psi _1$
by
![]() $\exists y(t_1 + S(y) = t_2)$
, we obtain a required equivalent
$\exists y(t_1 + S(y) = t_2)$
, we obtain a required equivalent
![]() $\Sigma _1$
formula
$\Sigma _1$
formula
![]() $\psi '$
. Since
$\psi '$
. Since
![]() $\mathbf {PA}(\mathbf {K}) \vdash \Box \psi \leftrightarrow \Box \psi '$
, to prove the theorem, it suffices to show that
$\mathbf {PA}(\mathbf {K}) \vdash \Box \psi \leftrightarrow \Box \psi '$
, to prove the theorem, it suffices to show that
![]() $\mathbf {PA}(\mathbf {K}) \vdash \varphi \to \Box \varphi $
for any
$\mathbf {PA}(\mathbf {K}) \vdash \varphi \to \Box \varphi $
for any
![]() $\Sigma _1$
formula
$\Sigma _1$
formula
![]() $\varphi $
such that it does not contain the connectives
$\varphi $
such that it does not contain the connectives
![]() $\neg $
and
$\neg $
and
![]() $\to $
, and that every atomic formula contained in
$\to $
, and that every atomic formula contained in
![]() $\varphi $
is of the form
$\varphi $
is of the form
![]() $t_1 = t_2$
for some
$t_1 = t_2$
for some
![]() $\mathcal {L}_A$
-terms
$\mathcal {L}_A$
-terms
![]() $t_1$
and
$t_1$
and
![]() $t_2$
.
$t_2$
.
This theorem is proved by induction on the construction of
![]() $\varphi $
. If
$\varphi $
. If
![]() $\varphi $
is
$\varphi $
is
![]() $t_1 = t_2$
, then
$t_1 = t_2$
, then
![]() $\mathbf {PA}(\mathbf {K}) \vdash t_1 = t_2 \to \Box t_1 = t_2$
follows from
$\mathbf {PA}(\mathbf {K}) \vdash t_1 = t_2 \to \Box t_1 = t_2$
follows from
![]() $\mathbf {PA}(\mathbf {K}) \vdash x = y \to \Box x = y$
(Proposition 2.1) by substituting
$\mathbf {PA}(\mathbf {K}) \vdash x = y \to \Box x = y$
(Proposition 2.1) by substituting
![]() $t_1$
and
$t_1$
and
![]() $t_2$
into
$t_2$
into
![]() $x$
and y, respectively. The cases for
$x$
and y, respectively. The cases for
![]() $\land $
,
$\land $
,
![]() $\lor $
,
$\lor $
,
![]() $\forall x < t$
and
$\forall x < t$
and
![]() $\exists $
are proved as in the proof of Theorem 3.13.
$\exists $
are proved as in the proof of Theorem 3.13.
3 Classes of
 $\mathcal {L}_A(\Box )$
-formulas
$\mathcal {L}_A(\Box )$
-formulas
In first-order arithmetic, it is important to classify
![]() $\mathcal {L}_A$
-formulas according to the arithmetic hierarchy. In this section, we introduce three classes
$\mathcal {L}_A$
-formulas according to the arithmetic hierarchy. In this section, we introduce three classes
![]() $\mathrm {B}$
,
$\mathrm {B}$
,
![]() $\Delta (\mathrm {B})$
, and
$\Delta (\mathrm {B})$
, and
![]() $\Sigma (\mathrm {B})$
of
$\Sigma (\mathrm {B})$
of
![]() $\mathcal {L}_A(\Box )$
-formulas, and investigate basic properties of formulas in these classes. Our classes
$\mathcal {L}_A(\Box )$
-formulas, and investigate basic properties of formulas in these classes. Our classes
![]() $\Delta (\mathrm {B})$
and
$\Delta (\mathrm {B})$
and
![]() $\Sigma (\mathrm {B})$
are modal arithmetical counterparts of
$\Sigma (\mathrm {B})$
are modal arithmetical counterparts of
![]() $\Delta _0$
and
$\Delta _0$
and
![]() $\Sigma _1$
, respectively.
$\Sigma _1$
, respectively.
Definition 3.9 (
 $\mathrm {B}$
,
$\mathrm {B}$
,
 $\Delta (\mathrm {B})$
, and
$\Delta (\mathrm {B})$
, and
 $\Sigma (\mathrm {B})$
)
$\Sigma (\mathrm {B})$
)
-
• Let
 $\mathrm {B}$
be the class of all
$\mathrm {B}$
be the class of all
 $\mathcal {L}_A(\Box )$
-formulas of the form
$\mathcal {L}_A(\Box )$
-formulas of the form
 $\Box \varphi $
.
$\Box \varphi $
. -
• Let
 $\Delta (\mathrm {B})$
be the smallest class of
$\Delta (\mathrm {B})$
be the smallest class of
 $\mathcal {L}_A(\Box )$
-formulas satisfying the following conditions:
$\mathcal {L}_A(\Box )$
-formulas satisfying the following conditions:-
1.
 $\Delta _0 \cup \mathrm {B} \subseteq \Delta (\mathrm {B})$
.
$\Delta _0 \cup \mathrm {B} \subseteq \Delta (\mathrm {B})$
. -
2. If
 $\varphi $
and
$\varphi $
and
 $\psi $
are in
$\psi $
are in
 $\Delta (\mathrm {B})$
, then so are
$\Delta (\mathrm {B})$
, then so are
 $\varphi \land \psi $
,
$\varphi \land \psi $
,
 $\varphi \lor \psi $
,
$\varphi \lor \psi $
,
 $\forall x < t\, \varphi $
and
$\forall x < t\, \varphi $
and
 $\exists x < t\, \varphi $
, where
$\exists x < t\, \varphi $
, where
 $t$
is an
$t$
is an
 $\mathcal {L}_A$
-term in which
$\mathcal {L}_A$
-term in which
 $x$
does not occur.
$x$
does not occur.
-
-
• Let
 $\Sigma (\mathrm {B})$
be the smallest class of
$\Sigma (\mathrm {B})$
be the smallest class of
 $\mathcal {L}_A(\Box )$
-formulas satisfying the following conditions:
$\mathcal {L}_A(\Box )$
-formulas satisfying the following conditions:-
1.
 $\Sigma _1 \cup \mathrm {B} \subseteq \Sigma (\mathrm {B})$
.
$\Sigma _1 \cup \mathrm {B} \subseteq \Sigma (\mathrm {B})$
. -
2. If
 $\varphi $
and
$\varphi $
and
 $\psi $
are in
$\psi $
are in
 $\Sigma (\mathrm {B})$
, then so are
$\Sigma (\mathrm {B})$
, then so are
 $\varphi \land \psi $
,
$\varphi \land \psi $
,
 $\varphi \lor \psi $
,
$\varphi \lor \psi $
,
 $\exists x \varphi $
and
$\exists x \varphi $
and
 $\forall x < t\, \varphi $
, where
$\forall x < t\, \varphi $
, where
 $t$
is an
$t$
is an
 $\mathcal {L}_A$
-term in which
$\mathcal {L}_A$
-term in which
 $x$
does not occur.
$x$
does not occur.
-
We emphasize here that in some sense the class
![]() $\Sigma (\mathrm {B})$
is a natural extension of the class
$\Sigma (\mathrm {B})$
is a natural extension of the class
![]() $\Sigma _1$
. For each r.e. theory T, let
$\Sigma _1$
. For each r.e. theory T, let
![]() $\mathrm {Pr}_T(x)$
be a fixed
$\mathrm {Pr}_T(x)$
be a fixed
![]() $\Sigma _1$
provability predicate of T. In the context of interpreting
$\Sigma _1$
provability predicate of T. In the context of interpreting
![]() $\Box $
by
$\Box $
by
![]() $\mathrm {Pr}_T(x)$
, each
$\mathrm {Pr}_T(x)$
, each
![]() $\mathcal {L}_A(\Box )$
-formula of the form
$\mathcal {L}_A(\Box )$
-formula of the form
![]() $\Box \varphi $
is interpreted by a
$\Box \varphi $
is interpreted by a
![]() $\Sigma _1$
formula, and hence every
$\Sigma _1$
formula, and hence every
![]() $\Sigma (\mathrm {B})$
formula is also recognized as a
$\Sigma (\mathrm {B})$
formula is also recognized as a
![]() $\Sigma _1$
formula. From this perspective, we will attempt to extend the properties possessed by
$\Sigma _1$
formula. From this perspective, we will attempt to extend the properties possessed by
![]() $\Sigma _1$
formulas in first-order arithmetic to
$\Sigma _1$
formulas in first-order arithmetic to
![]() $\Sigma (\mathrm {B})$
formulas in modal arithmetic. Note, however, that
$\Sigma (\mathrm {B})$
formulas in modal arithmetic. Note, however, that
![]() $\Delta (\mathrm {B})$
, unlike
$\Delta (\mathrm {B})$
, unlike
![]() $\Delta _0$
, is not closed under taking negation and implication. For example, it can be shown that there is no
$\Delta _0$
, is not closed under taking negation and implication. For example, it can be shown that there is no
![]() $\Delta (\mathrm {B})$
sentence
$\Delta (\mathrm {B})$
sentence
![]() $\varphi $
such that
$\varphi $
such that
![]() $\mathbf {PA}(\mathbf {K}) \vdash \neg \Box \bot \leftrightarrow \varphi $
(see Corollary 3.12).
$\mathbf {PA}(\mathbf {K}) \vdash \neg \Box \bot \leftrightarrow \varphi $
(see Corollary 3.12).
The following proposition states that the relationship between
![]() $\Sigma (\mathrm {B})$
and
$\Sigma (\mathrm {B})$
and
![]() $\Delta (\mathrm {B})$
is similar to the relationship between
$\Delta (\mathrm {B})$
is similar to the relationship between
![]() $\Sigma _1$
and
$\Sigma _1$
and
![]() $\Delta _0$
.
$\Delta _0$
.
Proposition 3.10. For any
![]() $\Sigma (\mathrm {B})$
formula
$\Sigma (\mathrm {B})$
formula
![]() $\varphi $
, there exist a variable
$\varphi $
, there exist a variable
![]() $v $
and a
$v $
and a
![]() $\Delta (\mathrm {B})$
formula
$\Delta (\mathrm {B})$
formula
![]() $\psi $
such that
$\psi $
such that
![]() $\mathbf {PA}_{\Box } \vdash \varphi \leftrightarrow \exists v \psi $
.
$\mathbf {PA}_{\Box } \vdash \varphi \leftrightarrow \exists v \psi $
.
Proof. We prove the proposition by induction on the construction of
![]() $\varphi $
.
$\varphi $
.
-
• If
 $\varphi $
is
$\varphi $
is
 $\Sigma _1$
, then there exists a
$\Sigma _1$
, then there exists a
 $\Delta _0$
formula
$\Delta _0$
formula
 $\psi $
such that
$\psi $
such that
 $\mathbf {PA} \vdash \varphi \leftrightarrow \exists v \psi $
.
$\mathbf {PA} \vdash \varphi \leftrightarrow \exists v \psi $
. -
• If
 $\varphi $
is of the form
$\varphi $
is of the form
 $\Box \varphi _0$
, then
$\Box \varphi _0$
, then
 $\varphi \in \Delta (\mathrm {B})$
and
$\varphi \in \Delta (\mathrm {B})$
and
 $\mathbf {PA}_{\Box } \vdash \varphi \leftrightarrow \exists v \varphi $
for a variable
$\mathbf {PA}_{\Box } \vdash \varphi \leftrightarrow \exists v \varphi $
for a variable
 $v $
not contained in
$v $
not contained in
 $\varphi $
.
$\varphi $
. -
• Let
 $\circ \in \{\land , \lor \}$
. If
$\circ \in \{\land , \lor \}$
. If
 $\varphi $
is of the form
$\varphi $
is of the form
 $\varphi _0 \circ \varphi _1$
, then by the induction hypothesis, there exist distinct variables
$\varphi _0 \circ \varphi _1$
, then by the induction hypothesis, there exist distinct variables
 $v_0$
and
$v_0$
and
 $v_1$
and
$v_1$
and
 $\Delta (\mathrm {B})$
formulas
$\Delta (\mathrm {B})$
formulas
 $\psi _0$
and
$\psi _0$
and
 $\psi _1$
such that
$\psi _1$
such that
 $\mathbf {PA}_{\Box }$
proves
$\mathbf {PA}_{\Box }$
proves
 $\varphi _0 \leftrightarrow \exists v_0 \psi _0$
and
$\varphi _0 \leftrightarrow \exists v_0 \psi _0$
and
 $\varphi _1 \leftrightarrow \exists v_1 \psi _1$
. Let
$\varphi _1 \leftrightarrow \exists v_1 \psi _1$
. Let
 $v $
be any variable that does not occur in
$v $
be any variable that does not occur in
 $\psi _0$
or
$\psi _0$
or
 $\psi _1$
, and is not
$\psi _1$
, and is not
 $v_0$
or
$v_0$
or
 $v_1$
. Then,
$v_1$
. Then,
 $\mathbf {PA}_{\Box }$
proves the equivalence
$\mathbf {PA}_{\Box }$
proves the equivalence
 $\varphi \leftrightarrow \exists v \, \exists v_0 < v \, \exists v_1 < v \, (\psi _0 \circ \psi _1)$
.
$\varphi \leftrightarrow \exists v \, \exists v_0 < v \, \exists v_1 < v \, (\psi _0 \circ \psi _1)$
. -
• If
 $\varphi $
is of the form
$\varphi $
is of the form
 $\exists x \varphi _0$
, then by the induction hypothesis, there exist a variable
$\exists x \varphi _0$
, then by the induction hypothesis, there exist a variable
 $v_0$
and a
$v_0$
and a
 $\Delta (\mathrm {B})$
formula
$\Delta (\mathrm {B})$
formula
 $\psi _0$
such that
$\psi _0$
such that
 $\mathbf {PA} \vdash \varphi _0 \leftrightarrow \exists v_0 \psi _0$
. Let
$\mathbf {PA} \vdash \varphi _0 \leftrightarrow \exists v_0 \psi _0$
. Let
 $v $
be any variable not contained in
$v $
be any variable not contained in
 $\psi _0$
and is not
$\psi _0$
and is not
 $v_0$
or
$v_0$
or
 $x$
. Then,
$x$
. Then,
 $\mathbf {PA}_{\Box }$
proves the equivalence
$\mathbf {PA}_{\Box }$
proves the equivalence
 $\varphi \leftrightarrow \exists v \, \exists x < v \, \exists v_0 < v \, \psi _0$
.
$\varphi \leftrightarrow \exists v \, \exists x < v \, \exists v_0 < v \, \psi _0$
. -
• The case that
 $\varphi $
is of the form
$\varphi $
is of the form
 $\exists x < t\, \varphi _0$
, where
$\exists x < t\, \varphi _0$
, where
 $t$
is an
$t$
is an
 $\mathcal {L}_A$
-term in which
$\mathcal {L}_A$
-term in which
 $x$
does not occur is proved as in the proof of the case of
$x$
does not occur is proved as in the proof of the case of
 $\exists $
.
$\exists $
. -
• Suppose
 $\varphi $
is of the form
$\varphi $
is of the form
 $\forall x < t\, \varphi _0$
, where
$\forall x < t\, \varphi _0$
, where
 $t$
is an
$t$
is an
 $\mathcal {L}_A$
-term in which
$\mathcal {L}_A$
-term in which
 $x$
does not occur. By the induction hypothesis, there exists a variable
$x$
does not occur. By the induction hypothesis, there exists a variable
 $v_0$
and a
$v_0$
and a
 $\Delta (\mathrm {B})$
formula
$\Delta (\mathrm {B})$
formula
 $\psi _0$
such that
$\psi _0$
such that
 $\mathbf {PA}_{\Box } \vdash \varphi _0 \leftrightarrow \exists v_0 \psi _0$
. Then,
$\mathbf {PA}_{\Box } \vdash \varphi _0 \leftrightarrow \exists v_0 \psi _0$
. Then,
 $\mathbf {PA}_{\Box } \vdash \varphi \leftrightarrow \forall x < t\, \exists v_0 \psi _0$
. By the collection principle for
$\mathbf {PA}_{\Box } \vdash \varphi \leftrightarrow \forall x < t\, \exists v_0 \psi _0$
. By the collection principle for
 $\mathcal {L}_A(\Box )$
-formulas derived from the induction axioms for
$\mathcal {L}_A(\Box )$
-formulas derived from the induction axioms for
 $\mathcal {L}_A(\Box )$
-formulas, we obtain for some appropriate variable
$\mathcal {L}_A(\Box )$
-formulas, we obtain for some appropriate variable $$\begin{align*}\mathbf{PA}_{\Box} \vdash \varphi \leftrightarrow \exists v\, \forall x < t\, \exists v_0 < v\, \psi_0 \end{align*}$$
$$\begin{align*}\mathbf{PA}_{\Box} \vdash \varphi \leftrightarrow \exists v\, \forall x < t\, \exists v_0 < v\, \psi_0 \end{align*}$$
 $v $
.
$v $
.
Proposition 3.11. For any
![]() $\Delta (\mathrm {B})$
sentence
$\Delta (\mathrm {B})$
sentence
![]() $\varphi $
, there exist a natural number
$\varphi $
, there exist a natural number
![]() $k$
and sentences
$k$
and sentences
![]() $\psi _0, \ldots , \psi _{k-1}$
such that
$\psi _0, \ldots , \psi _{k-1}$
such that
![]() $\mathbf {PA}(\mathbf {K}) \vdash \varphi \leftrightarrow \bigvee _{i < k} \Box \psi _i$
. Here
$\mathbf {PA}(\mathbf {K}) \vdash \varphi \leftrightarrow \bigvee _{i < k} \Box \psi _i$
. Here
![]() $\bigvee _{i < 0} \Box \psi _i$
denotes
$\bigvee _{i < 0} \Box \psi _i$
denotes
![]() $\bot $
.
$\bot $
.
Proof. We prove the proposition by induction on the construction of
![]() $\varphi $
.
$\varphi $
.
-
• If
 $\varphi $
is a
$\varphi $
is a
 $\Delta _0$
sentence, then either
$\Delta _0$
sentence, then either
 $\mathbf {PA} \vdash \varphi $
or
$\mathbf {PA} \vdash \varphi $
or
 $\mathbf {PA} \vdash \neg \varphi $
. Thus,
$\mathbf {PA} \vdash \neg \varphi $
. Thus,
 $\mathbf {PA}(\mathbf {K}) \vdash \varphi \leftrightarrow \Box 0=0$
or
$\mathbf {PA}(\mathbf {K}) \vdash \varphi \leftrightarrow \Box 0=0$
or
 $\mathbf {PA}(\mathbf {K}) \vdash \varphi \leftrightarrow \bot $
.
$\mathbf {PA}(\mathbf {K}) \vdash \varphi \leftrightarrow \bot $
. -
• If
 $\varphi $
is of the form
$\varphi $
is of the form
 $\Box \psi $
, then the statement is trivial.
$\Box \psi $
, then the statement is trivial. -
• If
 $\varphi $
is of the form
$\varphi $
is of the form
 $\psi \land \sigma $
, then there exist sentences
$\psi \land \sigma $
, then there exist sentences
 $\xi _0, \ldots , \xi _{k-1}, \eta _0, \ldots , \eta _{l-1}$
such that
$\xi _0, \ldots , \xi _{k-1}, \eta _0, \ldots , \eta _{l-1}$
such that
 $\mathbf {PA}(\mathbf {K}) \vdash \psi \leftrightarrow \bigvee _{i < k} \Box \xi _i$
and
$\mathbf {PA}(\mathbf {K}) \vdash \psi \leftrightarrow \bigvee _{i < k} \Box \xi _i$
and
 $\mathbf {PA}(\mathbf {K}) \vdash \sigma \leftrightarrow \bigvee _{j < l} \Box \eta _j$
. Then,
$\mathbf {PA}(\mathbf {K}) \vdash \sigma \leftrightarrow \bigvee _{j < l} \Box \eta _j$
. Then,
 $\mathbf {PA}(\mathbf {K}) \vdash \varphi \leftrightarrow \bigvee _{i < k} \bigvee _{j < l} \Box (\xi _i \land \eta _j)$
.
$\mathbf {PA}(\mathbf {K}) \vdash \varphi \leftrightarrow \bigvee _{i < k} \bigvee _{j < l} \Box (\xi _i \land \eta _j)$
. -
• If
 $\varphi $
is of the form
$\varphi $
is of the form
 $\psi \lor \sigma $
, then the statement is obvious by the induction hypothesis.
$\psi \lor \sigma $
, then the statement is obvious by the induction hypothesis. -
• If
 $\varphi $
is of the form
$\varphi $
is of the form
 $\exists y < t\, \psi (y)$
for some
$\exists y < t\, \psi (y)$
for some
 $\mathcal {L}_A$
-term
$\mathcal {L}_A$
-term
 $t$
, then
$t$
, then
 $t$
is a closed term because
$t$
is a closed term because
 $\varphi $
is a sentence. Let m be the value of
$\varphi $
is a sentence. Let m be the value of
 $t$
, then
$t$
, then
 $\mathbf {PA}(\mathbf {K}) \vdash \varphi \leftrightarrow \bigvee _{i < m} \psi (\overline {i})$
. Then, the statement holds by the induction hypothesis.
$\mathbf {PA}(\mathbf {K}) \vdash \varphi \leftrightarrow \bigvee _{i < m} \psi (\overline {i})$
. Then, the statement holds by the induction hypothesis. -
• If
 $\varphi $
is of the form
$\varphi $
is of the form
 $\forall y < t\, \psi (y)$
for some closed
$\forall y < t\, \psi (y)$
for some closed
 $\mathcal {L}_A$
-term
$\mathcal {L}_A$
-term
 $t$
, then for the value m of the term
$t$
, then for the value m of the term
 $t$
,
$t$
,
 $\mathbf {PA}(\mathbf {K}) \vdash \varphi \leftrightarrow \bigwedge _{i < m} \psi (\overline {i})$
. We can prove the statement by the induction hypothesis as in the proof of the case
$\mathbf {PA}(\mathbf {K}) \vdash \varphi \leftrightarrow \bigwedge _{i < m} \psi (\overline {i})$
. We can prove the statement by the induction hypothesis as in the proof of the case
 $\land $
.
$\land $
.
Corollary 3.12. Let T be a theory extending
![]() $\mathbf {PA}(\mathbf {K})$
such that
$\mathbf {PA}(\mathbf {K})$
such that
![]() $T \nvdash \Box \bot $
and
$T \nvdash \Box \bot $
and
![]() $T \nvdash \neg \Box \bot $
. Then, there is no
$T \nvdash \neg \Box \bot $
. Then, there is no
![]() $\Delta (\mathrm {B})$
sentence
$\Delta (\mathrm {B})$
sentence
![]() $\varphi $
such that
$\varphi $
such that
![]() $T \vdash \neg \Box \bot \leftrightarrow \varphi $
.
$T \vdash \neg \Box \bot \leftrightarrow \varphi $
.
Proof. Suppose, towards a contradiction, that
![]() $\varphi $
is a
$\varphi $
is a
![]() $\Delta (\mathrm {B})$
sentence such that
$\Delta (\mathrm {B})$
sentence such that
![]() $T \vdash \neg \Box \bot \leftrightarrow \varphi $
. By Proposition 3.11, there exist
$T \vdash \neg \Box \bot \leftrightarrow \varphi $
. By Proposition 3.11, there exist
![]() $k$
and
$k$
and
![]() $\psi _0, \ldots , \psi _{k-1}$
such that
$\psi _0, \ldots , \psi _{k-1}$
such that
![]() $\mathbf {PA}(\mathbf {K}) \vdash \varphi \leftrightarrow \bigvee _{i < k} \Box \psi _i$
. Then,
$\mathbf {PA}(\mathbf {K}) \vdash \varphi \leftrightarrow \bigvee _{i < k} \Box \psi _i$
. Then,
![]() $T \vdash \neg \Box \bot \leftrightarrow \bigvee _{i < k} \Box \psi _i$
. Since
$T \vdash \neg \Box \bot \leftrightarrow \bigvee _{i < k} \Box \psi _i$
. Since
![]() $T \nvdash \Box \bot $
, we get
$T \nvdash \Box \bot $
, we get
![]() $k> 0$
. Then,
$k> 0$
. Then,
![]() $T \vdash \Box \psi _0 \to \neg \Box \bot $
. On the other hand,
$T \vdash \Box \psi _0 \to \neg \Box \bot $
. On the other hand,
![]() $T \vdash \neg \Box \psi _0 \to \neg \Box \bot $
because T is an extension of
$T \vdash \neg \Box \psi _0 \to \neg \Box \bot $
because T is an extension of
![]() $\mathbf {PA}(\mathbf {K})$
. Therefore, we obtain
$\mathbf {PA}(\mathbf {K})$
. Therefore, we obtain
![]() $T \vdash \neg \Box \bot $
. This is a contradiction.
$T \vdash \neg \Box \bot $
. This is a contradiction.
We naturally extend Theorem 2.8 into the framework of modal arithmetic.
Theorem 3.13 (Formalized
 $\Sigma (\mathrm {B})$
-completeness theorem)
$\Sigma (\mathrm {B})$
-completeness theorem)
For any
![]() $\varphi \in \Sigma (\mathrm {B})$
,
$\varphi \in \Sigma (\mathrm {B})$
,
![]() $\mathbf {PA}(\mathbf {K4}) \vdash \varphi \to \Box \varphi $
.
$\mathbf {PA}(\mathbf {K4}) \vdash \varphi \to \Box \varphi $
.
Proof. We prove the theorem by induction on the construction of
![]() $\varphi $
.
$\varphi $
.
-
• If
 $\varphi $
is a
$\varphi $
is a
 $\Sigma _1$
formula, then
$\Sigma _1$
formula, then
 $\mathbf {PA}(\mathbf {K}) \vdash \varphi \to \Box \varphi $
by Theorem 2.8.
$\mathbf {PA}(\mathbf {K}) \vdash \varphi \to \Box \varphi $
by Theorem 2.8. -
• If
 $\varphi $
is of the form
$\varphi $
is of the form
 $\Box \psi $
, then
$\Box \psi $
, then
 $\mathbf {PA}(\mathbf {K4}) \vdash \varphi \to \Box \varphi $
.
$\mathbf {PA}(\mathbf {K4}) \vdash \varphi \to \Box \varphi $
. -
• If
 $\varphi $
is
$\varphi $
is
 $\psi \land \sigma $
, then by the induction hypothesis,
$\psi \land \sigma $
, then by the induction hypothesis,
 $\mathbf {PA}(\mathbf {K4}) \vdash \varphi \to \Box \psi \land \Box \sigma $
. We have
$\mathbf {PA}(\mathbf {K4}) \vdash \varphi \to \Box \psi \land \Box \sigma $
. We have
 $\mathbf {PA}(\mathbf {K4}) \vdash \varphi \to \Box \varphi $
.
$\mathbf {PA}(\mathbf {K4}) \vdash \varphi \to \Box \varphi $
. -
• If
 $\varphi $
is
$\varphi $
is
 $\psi \lor \sigma $
, then by the induction hypothesis,
$\psi \lor \sigma $
, then by the induction hypothesis,
 $\mathbf {PA}(\mathbf {K4})$
proves
$\mathbf {PA}(\mathbf {K4})$
proves
 $\psi \to \Box (\psi \lor \sigma )$
and
$\psi \to \Box (\psi \lor \sigma )$
and
 $\sigma \to \Box (\psi \lor \sigma )$
. Hence,
$\sigma \to \Box (\psi \lor \sigma )$
. Hence,
 $\mathbf {PA}(\mathbf {K4}) \vdash \varphi \to \Box \varphi $
.
$\mathbf {PA}(\mathbf {K4}) \vdash \varphi \to \Box \varphi $
. -
• Suppose that
 $\varphi $
is
$\varphi $
is
 $\exists x \psi $
. Since
$\exists x \psi $
. Since
 $\mathbf {PA}(\mathbf {K}) \vdash \psi \to \exists x \psi $
, we have
$\mathbf {PA}(\mathbf {K}) \vdash \psi \to \exists x \psi $
, we have
 $\mathbf {PA}(\mathbf {K}) \vdash \Box \psi \to \Box \exists x \psi $
. By the induction hypothesis,
$\mathbf {PA}(\mathbf {K}) \vdash \Box \psi \to \Box \exists x \psi $
. By the induction hypothesis,
 $\mathbf {PA}(\mathbf{K4}) \vdash \psi \to \Box \psi $
. Thus,
$\mathbf {PA}(\mathbf{K4}) \vdash \psi \to \Box \psi $
. Thus,
 $\mathbf {PA}(\mathbf{K4}) \vdash \psi \to \Box \exists x \psi $
. Then, we obtain
$\mathbf {PA}(\mathbf{K4}) \vdash \psi \to \Box \exists x \psi $
. Then, we obtain
 $\mathbf {PA}(\mathbf {K4}) \vdash \varphi \to \Box \varphi $
.
$\mathbf {PA}(\mathbf {K4}) \vdash \varphi \to \Box \varphi $
. -
• Before proving the case that
 $\varphi $
is of the form
$\varphi $
is of the form
 $\forall x < t\, \psi (x)$
generally, we prove the restricted case that
$\forall x < t\, \psi (x)$
generally, we prove the restricted case that
 $t$
is some variable y not occurring in
$t$
is some variable y not occurring in
 $\psi $
. Suppose that
$\psi $
. Suppose that
 $\varphi (y)$
is of the form
$\varphi (y)$
is of the form
 $\forall x < y\, \psi (x)$
for some variable y not occurring in
$\forall x < y\, \psi (x)$
for some variable y not occurring in
 $\psi (x)$
. Let
$\psi (x)$
. Let
 $\xi (y)$
be the formula
$\xi (y)$
be the formula
 $\varphi (y) \to \Box \varphi (y)$
, and then we prove
$\varphi (y) \to \Box \varphi (y)$
, and then we prove
 $\mathbf {PA}(\mathbf {K}) \vdash \forall y \xi (y)$
by using the induction axiom.
$\mathbf {PA}(\mathbf {K}) \vdash \forall y \xi (y)$
by using the induction axiom.For the base step, since trivially
 $\mathbf {PA}(\mathbf {K}) \vdash \forall x < 0\, \psi (x)$
, we have
$\mathbf {PA}(\mathbf {K}) \vdash \forall x < 0\, \psi (x)$
, we have
 $\mathbf {PA}(\mathbf {K}) \vdash \Box \varphi (0)$
and hence
$\mathbf {PA}(\mathbf {K}) \vdash \Box \varphi (0)$
and hence
 $\mathbf {PA}(\mathbf {K}) \vdash \xi (0)$
.
$\mathbf {PA}(\mathbf {K}) \vdash \xi (0)$
.For the induction step, since
we have $$\begin{align*}\mathbf{PA}(\mathbf{K}) \vdash [\forall x < S(y)\, \psi(x)] \leftrightarrow [(\forall x < y\, \psi(x)) \land \psi(y)], \end{align*}$$
(1)By the induction hypothesis,
$$\begin{align*}\mathbf{PA}(\mathbf{K}) \vdash [\forall x < S(y)\, \psi(x)] \leftrightarrow [(\forall x < y\, \psi(x)) \land \psi(y)], \end{align*}$$
(1)By the induction hypothesis, $$ \begin{align} \mathbf{PA}(\mathbf{K}) \vdash \varphi(S(y)) \leftrightarrow [\varphi(y) \land \psi(y)]. \end{align} $$
$$ \begin{align} \mathbf{PA}(\mathbf{K}) \vdash \varphi(S(y)) \leftrightarrow [\varphi(y) \land \psi(y)]. \end{align} $$
 $\mathbf {PA}(\mathbf {K4}) \vdash \psi (y) \to \Box \psi (y)$
. By combining this with (1) and the definition of
$\mathbf {PA}(\mathbf {K4}) \vdash \psi (y) \to \Box \psi (y)$
. By combining this with (1) and the definition of
 $\xi (y)$
, Then, by (1) again,
$\xi (y)$
, Then, by (1) again, $$\begin{align*}\mathbf{PA}(\mathbf{K4}) \vdash \xi(y) \land \varphi(S(y)) \to \Box \varphi(y) \land \Box \psi(y). \end{align*}$$
Equivalently,
$$\begin{align*}\mathbf{PA}(\mathbf{K4}) \vdash \xi(y) \land \varphi(S(y)) \to \Box \varphi(y) \land \Box \psi(y). \end{align*}$$
Equivalently, $$\begin{align*}\mathbf{PA}(\mathbf{K4}) \vdash \xi(y) \land \varphi(S(y)) \to \Box \varphi(S(y)). \end{align*}$$
$$\begin{align*}\mathbf{PA}(\mathbf{K4}) \vdash \xi(y) \land \varphi(S(y)) \to \Box \varphi(S(y)). \end{align*}$$
 $\mathbf {PA}(\mathbf {K4}) \vdash \xi (y) \to \xi (S(y))$
.
$\mathbf {PA}(\mathbf {K4}) \vdash \xi (y) \to \xi (S(y))$
.
Therefore, by the induction axiom, we conclude
 $\mathbf {PA}(\mathbf {K4}) \vdash \forall y \xi (y)$
.
$\mathbf {PA}(\mathbf {K4}) \vdash \forall y \xi (y)$
.Finally, suppose that
 $\varphi $
is of the form
$\varphi $
is of the form
 $\forall x < t\, \psi $
for some
$\forall x < t\, \psi $
for some
 $\mathcal {L}_A$
-term
$\mathcal {L}_A$
-term
 $t$
. We have already proved that
$t$
. We have already proved that
 $\mathbf {PA}(\mathbf {K4})$
proves
$\mathbf {PA}(\mathbf {K4})$
proves
 $\forall x < y\, \psi \to \Box \forall x < y\, \psi $
for some variable y not occurring in
$\forall x < y\, \psi \to \Box \forall x < y\, \psi $
for some variable y not occurring in
 $\psi $
. By substituting
$\psi $
. By substituting
 $t$
for y in this formula, we obtain
$t$
for y in this formula, we obtain
 $\mathbf {PA}(\mathbf {K4}) \vdash \varphi \to \Box \varphi $
.
$\mathbf {PA}(\mathbf {K4}) \vdash \varphi \to \Box \varphi $
.
Corollary 3.14 (
 $\Sigma (\mathrm {B})$
-deduction theorem)
$\Sigma (\mathrm {B})$
-deduction theorem)
Let T be any extension of
![]() $\mathbf {PA}(\mathbf {K4})$
and let X be any set of
$\mathbf {PA}(\mathbf {K4})$
and let X be any set of
![]() $\Sigma (\mathrm {B})$
sentences. Then, for any
$\Sigma (\mathrm {B})$
sentences. Then, for any
![]() $\mathcal {L}_A(\Box )$
-formula
$\mathcal {L}_A(\Box )$
-formula
![]() $\varphi $
, if
$\varphi $
, if
![]() $T + X \vdash \varphi $
, then there exist
$T + X \vdash \varphi $
, then there exist
![]() $\sigma _0, \ldots , \sigma _{k-1} \in X$
such that
$\sigma _0, \ldots , \sigma _{k-1} \in X$
such that
![]() $T \vdash \sigma _0 \land \cdots \land \sigma _{k-1} \to \varphi $
.
$T \vdash \sigma _0 \land \cdots \land \sigma _{k-1} \to \varphi $
.
Proof. This is proved by induction on the length of a proof of
![]() $\varphi $
in
$\varphi $
in
![]() $T + X$
. We only give a proof of the case that
$T + X$
. We only give a proof of the case that
![]() $\varphi $
is derived from
$\varphi $
is derived from
![]() $\psi $
by the rule Nec. Then,
$\psi $
by the rule Nec. Then,
![]() $\varphi $
is of the form
$\varphi $
is of the form
![]() $\Box \psi $
. By the induction hypothesis,
$\Box \psi $
. By the induction hypothesis,
![]() $T \vdash \sigma _0 \land \cdots \land \sigma _{k-1} \to \psi $
for some
$T \vdash \sigma _0 \land \cdots \land \sigma _{k-1} \to \psi $
for some
![]() $\sigma _0, \ldots , \sigma _{k-1} \in X$
. Then,
$\sigma _0, \ldots , \sigma _{k-1} \in X$
. Then,
![]() $T \vdash \Box \sigma _0 \land \cdots \land \Box \sigma _{k-1} \to \Box \psi $
. By Theorem 3.13,
$T \vdash \Box \sigma _0 \land \cdots \land \Box \sigma _{k-1} \to \Box \psi $
. By Theorem 3.13,
![]() $T \vdash \sigma _0 \land \cdots \land \sigma _{k-1} \to \Box \psi $
.
$T \vdash \sigma _0 \land \cdots \land \sigma _{k-1} \to \Box \psi $
.
4
 $\mathrm {B}$
-
$\mathrm {B}$
-
 $\mathrm {DP}$
,
$\mathrm {DP}$
,
 $\Delta (\mathrm {B})$
-
$\Delta (\mathrm {B})$
-
 $\mathrm {DP}$
and related properties
$\mathrm {DP}$
and related properties
We introduce several versions of the partial disjunction property.
Definition 4.15. Let T be a theory and let
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Theta $
be classes of formulas.
$\Theta $
be classes of formulas.
-
• T is said to have the modal disjunction property (
 $\mathrm {MDP}$
) if for any sentences
$\mathrm {MDP}$
) if for any sentences
 $\varphi $
and
$\varphi $
and
 $\psi $
, if
$\psi $
, if
 $T \vdash \Box \varphi \lor \Box \psi $
, then
$T \vdash \Box \varphi \lor \Box \psi $
, then
 $T \vdash \varphi $
or
$T \vdash \varphi $
or
 $T \vdash \psi $
.
$T \vdash \psi $
. -
• T is said to have the modal existence property (
 $\mathrm {MEP}$
) if for any formula
$\mathrm {MEP}$
) if for any formula
 $\varphi (x)$
that has no free variables except
$\varphi (x)$
that has no free variables except
 $x$
, if
$x$
, if
 $T \vdash \exists x \Box \varphi (x)$
, then for some natural number
$T \vdash \exists x \Box \varphi (x)$
, then for some natural number
 $n$
,
$n$
,
 $T \vdash \varphi (\overline {n})$
.
$T \vdash \varphi (\overline {n})$
. -
• T is said to have the
 $\Gamma $
-disjunction property (
$\Gamma $
-disjunction property (
 $\Gamma $
-
$\Gamma $
-
 $\mathrm {DP}$
) if for any
$\mathrm {DP}$
) if for any
 $\Gamma $
sentences
$\Gamma $
sentences
 $\varphi $
and
$\varphi $
and
 $\psi $
, if
$\psi $
, if
 $T \vdash \varphi \lor \psi $
, then
$T \vdash \varphi \lor \psi $
, then
 $T \vdash \varphi $
or
$T \vdash \varphi $
or
 $T \vdash \psi $
.
$T \vdash \psi $
. -
• T is said to have the
 $\Gamma $
-existence property (
$\Gamma $
-existence property (
 $\Gamma $
-
$\Gamma $
-
 $\mathrm {EP}$
) if for any
$\mathrm {EP}$
) if for any
 $\Gamma $
formula
$\Gamma $
formula
 $\varphi (x)$
that has no free variables except
$\varphi (x)$
that has no free variables except
 $x$
, if
$x$
, if
 $T \vdash \exists x \varphi (x)$
, then for some natural number
$T \vdash \exists x \varphi (x)$
, then for some natural number
 $n$
,
$n$
,
 $T \vdash \varphi (\overline {n})$
.
$T \vdash \varphi (\overline {n})$
. -
• T is said to have the
 $(\Gamma , \Theta )$
-disjunction property (
$(\Gamma , \Theta )$
-disjunction property (
 $(\Gamma , \Theta )$
-
$(\Gamma , \Theta )$
-
 $\mathrm {DP}$
) if for any
$\mathrm {DP}$
) if for any
 $\Gamma $
sentence
$\Gamma $
sentence
 $\varphi $
and any
$\varphi $
and any
 $\Theta $
sentence
$\Theta $
sentence
 $\psi $
, if
$\psi $
, if
 $T \vdash \varphi \lor \psi $
, then
$T \vdash \varphi \lor \psi $
, then
 $T \vdash \varphi $
or
$T \vdash \varphi $
or
 $T \vdash \psi $
.
$T \vdash \psi $
. -
• For
 $n \geq 2$
, T is said to have the
$n \geq 2$
, T is said to have the
 $n$
-fold
$n$
-fold
 $\mathrm {B}$
-disjunction property (
$\mathrm {B}$
-disjunction property (
 $\mathrm {B}^n$
-
$\mathrm {B}^n$
-
 $\mathrm {DP}$
) if for any
$\mathrm {DP}$
) if for any
 $\mathcal {L}_A(\Box )$
-sentences
$\mathcal {L}_A(\Box )$
-sentences
 $\varphi _1, \ldots , \varphi _n$
, if
$\varphi _1, \ldots , \varphi _n$
, if
 $T \vdash \Box \varphi _1 \lor \cdots \lor \Box \varphi _n$
, then
$T \vdash \Box \varphi _1 \lor \cdots \lor \Box \varphi _n$
, then
 $T \vdash \Box \varphi _i$
for some
$T \vdash \Box \varphi _i$
for some
 $i \ (1 \leq i \leq n)$
.
$i \ (1 \leq i \leq n)$
. -
• If T is r.e., then T is said to be
 $\Gamma $
-disjunctively correct (
$\Gamma $
-disjunctively correct (
 $\Gamma $
-
$\Gamma $
-
 $\mathrm {DC}$
) if for any
$\mathrm {DC}$
) if for any
 $\Gamma $
sentence
$\Gamma $
sentence
 $\varphi $
, if
$\varphi $
, if
 $T \vdash \varphi \lor \mathrm {Pr}_T(\ulcorner \varphi \urcorner )$
, then
$T \vdash \varphi \lor \mathrm {Pr}_T(\ulcorner \varphi \urcorner )$
, then
 $T \vdash \varphi $
.
$T \vdash \varphi $
. -
• We say that T is closed under the box elimination rule if for any sentence
 $\varphi $
, if
$\varphi $
, if
 $T \vdash \Box \varphi $
, then
$T \vdash \Box \varphi $
, then
 $T \vdash \varphi $
.
$T \vdash \varphi $
.
Here
![]() $\mathrm {Pr}_T(x)$
is a fixed natural
$\mathrm {Pr}_T(x)$
is a fixed natural
![]() $\Sigma _1$
provability predicate of T. We also fix a primitive recursive proof predicate
$\Sigma _1$
provability predicate of T. We also fix a primitive recursive proof predicate
![]() $\mathrm {Prf}_T(x, y)$
of T saying that y encodes a T-proof of
$\mathrm {Prf}_T(x, y)$
of T saying that y encodes a T-proof of
![]() $x$
, whose existence is guaranteed by Craig’s trick.
$x$
, whose existence is guaranteed by Craig’s trick.
Of course,
![]() $(\Gamma , \Gamma )$
-
$(\Gamma , \Gamma )$
-
![]() $\mathrm {DP}$
and
$\mathrm {DP}$
and
![]() $\mathrm {B}^2$
-
$\mathrm {B}^2$
-
![]() $\mathrm {DP}$
are exactly
$\mathrm {DP}$
are exactly
![]() $\Gamma $
-
$\Gamma $
-
![]() $\mathrm {DP}$
and
$\mathrm {DP}$
and
![]() $\mathrm {B}$
-
$\mathrm {B}$
-
![]() $\mathrm {DP}$
, respectively. The notion of
$\mathrm {DP}$
, respectively. The notion of
![]() $\Gamma $
-
$\Gamma $
-
![]() $\mathrm {DC}$
was introduced in [Reference Kurahashi15]. It is known that for any consistent r.e. extension T of
$\mathrm {DC}$
was introduced in [Reference Kurahashi15]. It is known that for any consistent r.e. extension T of
![]() $\mathbf {PA}$
, T is
$\mathbf {PA}$
, T is
![]() $\Sigma _1$
-
$\Sigma _1$
-
![]() $\mathrm {DC}$
if and only if T is
$\mathrm {DC}$
if and only if T is
![]() $\Sigma _1$
-sound (cf. [Reference Kurahashi15]).
$\Sigma _1$
-sound (cf. [Reference Kurahashi15]).
Proposition 4.16. Let T be any extension of
![]() $\mathbf {PA}(\mathbf {K})$
.
$\mathbf {PA}(\mathbf {K})$
.
-
1. For any
 $n \geq 2$
, if T has
$n \geq 2$
, if T has
 $\mathrm {B}^{n+1}$
-
$\mathrm {B}^{n+1}$
-
 $\mathrm {DP}$
, then T also has
$\mathrm {DP}$
, then T also has
 $\mathrm {B}^n$
-
$\mathrm {B}^n$
-
 $\mathrm {DP}$
.
$\mathrm {DP}$
. -
2. T has
 $\mathrm {B}^n$
-
$\mathrm {B}^n$
-
 $\mathrm {DP}$
for all
$\mathrm {DP}$
for all
 $n \geq 2$
if and only if T has
$n \geq 2$
if and only if T has
 $\Delta (\mathrm {B})$
-
$\Delta (\mathrm {B})$
-
 $\mathrm {DP}$
.
$\mathrm {DP}$
.
Proof. 1. Let
![]() $\varphi _1, \ldots , \varphi _n$
be any sentences such that
$\varphi _1, \ldots , \varphi _n$
be any sentences such that
![]() $T \vdash \Box \varphi _1 \lor \cdots \lor \Box \varphi _n$
. Then,
$T \vdash \Box \varphi _1 \lor \cdots \lor \Box \varphi _n$
. Then,
![]() $T \vdash \Box \varphi _1 \lor \cdots \lor \Box \varphi _n \lor \Box \varphi _n$
. By
$T \vdash \Box \varphi _1 \lor \cdots \lor \Box \varphi _n \lor \Box \varphi _n$
. By
![]() $\mathrm {B}^{n+1}$
-
$\mathrm {B}^{n+1}$
-
![]() $\mathrm {DP}$
, for some i (
$\mathrm {DP}$
, for some i (
![]() $1 \leq i \leq n$
), we have
$1 \leq i \leq n$
), we have
![]() $T \vdash \Box \varphi _i$
.
$T \vdash \Box \varphi _i$
.
2.
![]() $(\Rightarrow )$
: Let
$(\Rightarrow )$
: Let
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
be any
$\psi $
be any
![]() $\Delta (\mathrm {B})$
sentences such that
$\Delta (\mathrm {B})$
sentences such that
![]() $T \vdash \varphi \lor \psi $
. By Proposition 3.11, there exist sentences
$T \vdash \varphi \lor \psi $
. By Proposition 3.11, there exist sentences
![]() $\varphi _0, \ldots , \varphi _{k-1}$
and
$\varphi _0, \ldots , \varphi _{k-1}$
and
![]() $\psi _0, \ldots , \psi _{l-1}$
such that
$\psi _0, \ldots , \psi _{l-1}$
such that
![]() $T \vdash \varphi \leftrightarrow \bigvee _{i < k} \Box \varphi _i$
and
$T \vdash \varphi \leftrightarrow \bigvee _{i < k} \Box \varphi _i$
and
![]() ${T \vdash \psi \leftrightarrow \bigvee _{j < l} \Box \psi _j}$
. Then,
${T \vdash \psi \leftrightarrow \bigvee _{j < l} \Box \psi _j}$
. Then,
![]() $T \vdash \bigvee _{i < k} \Box \varphi _i \lor \bigvee _{j < l} \Box \psi _j$
. If
$T \vdash \bigvee _{i < k} \Box \varphi _i \lor \bigvee _{j < l} \Box \psi _j$
. If
![]() $k = 0$
or
$k = 0$
or
![]() $l = 0$
, then we easily obtain
$l = 0$
, then we easily obtain
![]() $T \vdash \varphi $
or
$T \vdash \varphi $
or
![]() ${T \vdash \psi} $
. Thus, we may assume both
${T \vdash \psi} $
. Thus, we may assume both
![]() $k$
and l are larger than
$k$
and l are larger than
![]() $0$
. Then,
$0$
. Then,
![]() $k+l \geq 2$
. By
$k+l \geq 2$
. By
![]() $\mathrm {B}^{k+l}$
-
$\mathrm {B}^{k+l}$
-
![]() $\mathrm {DP}$
, there exists
$\mathrm {DP}$
, there exists
![]() $i < k$
or
$i < k$
or
![]() $j < l$
such that
$j < l$
such that
![]() $T \vdash \Box \varphi _i$
or
$T \vdash \Box \varphi _i$
or
![]() ${T \vdash \Box \psi _j}$
. Then, we obtain that
${T \vdash \Box \psi _j}$
. Then, we obtain that
![]() $T \vdash \varphi $
or
$T \vdash \varphi $
or
![]() $T \vdash \psi $
.
$T \vdash \psi $
.
![]() $(\Leftarrow )$
: We prove this implication by induction on
$(\Leftarrow )$
: We prove this implication by induction on
![]() $n \geq 2$
. Since
$n \geq 2$
. Since
![]() $\mathrm {B} \subseteq \Delta (\mathrm {B})$
, T has
$\mathrm {B} \subseteq \Delta (\mathrm {B})$
, T has
![]() $\mathrm {B}^2$
-
$\mathrm {B}^2$
-
![]() $\mathrm {DP}$
. Suppose that T has
$\mathrm {DP}$
. Suppose that T has
![]() $\mathrm {B}^n$
-
$\mathrm {B}^n$
-
![]() $\mathrm {DP}$
and we would like to prove that T also has
$\mathrm {DP}$
and we would like to prove that T also has
![]() $\mathrm {B}^{n+1}$
-
$\mathrm {B}^{n+1}$
-
![]() $\mathrm {DP}$
. Let
$\mathrm {DP}$
. Let
![]() $\varphi _1, \ldots , \varphi _n, \varphi _{n+1}$
be any sentences such that
$\varphi _1, \ldots , \varphi _n, \varphi _{n+1}$
be any sentences such that
![]() $T \vdash \Box \varphi _1 \lor \cdots \lor \Box \varphi _n \lor \Box \varphi _{n+1}$
. Since both
$T \vdash \Box \varphi _1 \lor \cdots \lor \Box \varphi _n \lor \Box \varphi _{n+1}$
. Since both
![]() $\Box \varphi _1 \lor \cdots \lor \Box \varphi _n$
and
$\Box \varphi _1 \lor \cdots \lor \Box \varphi _n$
and
![]() $\Box \varphi _{n+1}$
are
$\Box \varphi _{n+1}$
are
![]() $\Delta (\mathrm {B})$
sentences, we have
$\Delta (\mathrm {B})$
sentences, we have
![]() $T \vdash \Box \varphi _1 \lor \cdots \lor \Box \varphi _n$
or
$T \vdash \Box \varphi _1 \lor \cdots \lor \Box \varphi _n$
or
![]() $T \vdash \Box \varphi _{n+1}$
by
$T \vdash \Box \varphi _{n+1}$
by
![]() $\Delta (\mathrm {B})$
-
$\Delta (\mathrm {B})$
-
![]() $\mathrm {DP}$
. In the former case, we obtain
$\mathrm {DP}$
. In the former case, we obtain
![]() $T \vdash \Box \varphi _i$
for some i (
$T \vdash \Box \varphi _i$
for some i (
![]() $1 \leq i \leq n$
) by the induction hypothesis. We have proved that T has
$1 \leq i \leq n$
) by the induction hypothesis. We have proved that T has
![]() $\mathrm {B}^{n+1}$
-
$\mathrm {B}^{n+1}$
-
![]() $\mathrm {DP}$
.
$\mathrm {DP}$
.
The following proposition is immediate from the definitions.
Proposition 4.17. Let T be any
![]() $\mathcal {L}_A(\Box )$
-theory.
$\mathcal {L}_A(\Box )$
-theory.
-
1. T has
 $\mathrm {MDP}$
if and only if T has
$\mathrm {MDP}$
if and only if T has
 $\mathrm {B}$
-
$\mathrm {B}$
-
 $\mathrm {DP}$
and is closed under the box elimination rule.
$\mathrm {DP}$
and is closed under the box elimination rule. -
2. T has
 $\mathrm {MEP}$
if and only if T has
$\mathrm {MEP}$
if and only if T has
 $\mathrm {B}$
-
$\mathrm {B}$
-
 $\mathrm {EP}$
and is closed under the box elimination rule.
$\mathrm {EP}$
and is closed under the box elimination rule.
We show that each existence property yields the corresponding disjunction property.
Proposition 4.18. Let T be any
![]() $\mathcal {L}_A(\Box )$
-theory.
$\mathcal {L}_A(\Box )$
-theory.
-
1. If T is an extension of
 $\mathbf {PA}(\mathbf {K})$
and T has
$\mathbf {PA}(\mathbf {K})$
and T has
 $\mathrm {MEP}$
(resp.
$\mathrm {MEP}$
(resp.
 $\mathrm {B}$
-
$\mathrm {B}$
-
 $\mathrm {EP}$
), then T has
$\mathrm {EP}$
), then T has
 $\mathrm {MDP}$
(resp.
$\mathrm {MDP}$
(resp.
 $\mathrm {B}$
-
$\mathrm {B}$
-
 $\mathrm {DP}$
).
$\mathrm {DP}$
). -
2. If T has
 $\Delta (\mathrm {B})$
-
$\Delta (\mathrm {B})$
-
 $\mathrm {EP}$
(resp.
$\mathrm {EP}$
(resp.
 $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
 $\mathrm {EP}$
), then T has
$\mathrm {EP}$
), then T has
 $\Delta (\mathrm {B})$
-
$\Delta (\mathrm {B})$
-
 $\mathrm {DP}$
(resp.
$\mathrm {DP}$
(resp.
 $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
 $\mathrm {DP}$
).
$\mathrm {DP}$
).
Proof. We only give a proof of Clause 1 for
![]() $\mathrm {MEP}$
and
$\mathrm {MEP}$
and
![]() $\mathrm {MDP}$
. Let
$\mathrm {MDP}$
. Let
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
be any sentences such that
$\psi $
be any sentences such that
![]() $T \vdash \Box \varphi \lor \Box \psi $
. Then,
$T \vdash \Box \varphi \lor \Box \psi $
. Then,
![]() $T \vdash \exists x \Box \bigl ((x = 0 \land \varphi ) \lor (x \neq 0 \land \psi ) \bigr )$
. By
$T \vdash \exists x \Box \bigl ((x = 0 \land \varphi ) \lor (x \neq 0 \land \psi ) \bigr )$
. By
![]() $\mathrm {MEP}$
, there exists a natural number
$\mathrm {MEP}$
, there exists a natural number
![]() $n$
such that
$n$
such that
![]() $T \vdash (\overline {n} = 0 \land \varphi ) \lor (\overline {n} \neq 0 \land \psi )$
. If
$T \vdash (\overline {n} = 0 \land \varphi ) \lor (\overline {n} \neq 0 \land \psi )$
. If
![]() $n=0$
,
$n=0$
,
![]() $T \vdash \varphi $
; if
$T \vdash \varphi $
; if
![]() $n \neq 0$
,
$n \neq 0$
,
![]() $T \vdash \psi $
. Therefore, T has
$T \vdash \psi $
. Therefore, T has
![]() $\mathrm {MDP}$
.
$\mathrm {MDP}$
.
In the literature so far, modal disjunction and existence properties in modal arithmetic have been considered only for theories which are closed under the box elimination rule. As shown in Proposition 4.17, if T is closed under the box elimination rule, then
![]() $\mathrm {MDP}$
and
$\mathrm {MDP}$
and
![]() $\mathrm {B}$
-
$\mathrm {B}$
-
![]() $\mathrm {DP}$
are equivalent. Hence,
$\mathrm {DP}$
are equivalent. Hence,
![]() $\mathrm {MDP}$
and
$\mathrm {MDP}$
and
![]() $\mathrm {B}$
-
$\mathrm {B}$
-
![]() $\mathrm {DP}$
have often been identified in the literature. Since the present paper also deals with theories that are not necessarily closed under the box elimination rule, we distinguish between
$\mathrm {DP}$
have often been identified in the literature. Since the present paper also deals with theories that are not necessarily closed under the box elimination rule, we distinguish between
![]() $\mathrm {MDP}$
and
$\mathrm {MDP}$
and
![]() $\mathrm {B}$
-
$\mathrm {B}$
-
![]() $\mathrm {DP}$
. In fact, as Figure 1 shows, there seems to be a large gap between the strength of these properties.
$\mathrm {DP}$
. In fact, as Figure 1 shows, there seems to be a large gap between the strength of these properties.
We explore nontrivial implications between
![]() $\Delta (\mathrm {B})$
-
$\Delta (\mathrm {B})$
-
![]() $\mathrm {DP}$
,
$\mathrm {DP}$
,
![]() $(\Delta (\mathrm {B}), \Sigma _1)$
-
$(\Delta (\mathrm {B}), \Sigma _1)$
-
![]() $\mathrm {DP}$
,
$\mathrm {DP}$
,
![]() $\Delta (\mathrm {B})$
-
$\Delta (\mathrm {B})$
-
![]() $\mathrm {DC}$
,
$\mathrm {DC}$
,
![]() $\mathrm {B}$
-
$\mathrm {B}$
-
![]() $\mathrm {DP}$
,
$\mathrm {DP}$
,
![]() $(\mathrm {B}, \Sigma _1)$
-
$(\mathrm {B}, \Sigma _1)$
-
![]() $\mathrm {DP}$
, and
$\mathrm {DP}$
, and
![]() $\mathrm {B}$
-
$\mathrm {B}$
-
![]() $\mathrm {DC}$
.
$\mathrm {DC}$
.
Lemma 4.19. Let T be any r.e. extension of
![]() $\mathbf {PA}(\mathbf {K})$
having
$\mathbf {PA}(\mathbf {K})$
having
![]() $\mathrm {B}^{n+1}$
-
$\mathrm {B}^{n+1}$
-
![]() $\mathrm {DP}$
. Then, for any
$\mathrm {DP}$
. Then, for any
![]() $\mathcal {L}_A(\Box )$
-sentences
$\mathcal {L}_A(\Box )$
-sentences
![]() $\varphi _1, \ldots , \varphi _n$
and
$\varphi _1, \ldots , \varphi _n$
and
![]() $\Sigma _1$
sentence
$\Sigma _1$
sentence
![]() $\sigma $
, if
$\sigma $
, if
![]() $T \vdash \Box \varphi _1 \lor \cdots \lor \Box \varphi _n \lor \sigma $
, then
$T \vdash \Box \varphi _1 \lor \cdots \lor \Box \varphi _n \lor \sigma $
, then
![]() $T \vdash \Box \varphi _i$
for some
$T \vdash \Box \varphi _i$
for some
![]() $i \ (1 \leq i \leq n)$
or
$i \ (1 \leq i \leq n)$
or
![]() $T \vdash \sigma $
.
$T \vdash \sigma $
.
Proof. Suppose
![]() $T \vdash \Box \varphi _1 \lor \cdots \lor \Box \varphi _n \lor \sigma $
and
$T \vdash \Box \varphi _1 \lor \cdots \lor \Box \varphi _n \lor \sigma $
and
![]() $T \nvdash \sigma $
, and we would like to show
$T \nvdash \sigma $
, and we would like to show
![]() $T \vdash \Box \varphi _i$
for some i. We may assume that
$T \vdash \Box \varphi _i$
for some i. We may assume that
![]() $\sigma $
is of the form
$\sigma $
is of the form
![]() $\exists x \delta (x)$
for some
$\exists x \delta (x)$
for some
![]() $\Delta _0$
formula
$\Delta _0$
formula
![]() $\delta (x)$
. Then,
$\delta (x)$
. Then,
![]() $\mathbb {N} \models \forall x \neg \delta (x)$
because
$\mathbb {N} \models \forall x \neg \delta (x)$
because
![]() $T \nvdash \sigma $
. By the Fixed Point Lemma, for each i with
$T \nvdash \sigma $
. By the Fixed Point Lemma, for each i with
![]() $1 \leq i \leq n$
, let
$1 \leq i \leq n$
, let
![]() $\psi _i^0$
and
$\psi _i^0$
and
![]() $\psi _i^1$
be
$\psi _i^1$
be
![]() $\Sigma _1$
sentences satisfying the following equivalences:
$\Sigma _1$
sentences satisfying the following equivalences:
-
•
 $\mathbf {PA} \vdash \psi _i^0 \leftrightarrow \exists x \Bigl ( \bigl (\delta (x) \lor \mathrm {Prf}_T(\ulcorner \Box \psi _i^1\urcorner , x) \bigr ) \land \forall y < x \, \neg \mathrm {Prf}_T(\ulcorner \Box (\varphi _i \lor \psi _i^0)\urcorner , y) \Bigr )$
,
$\mathbf {PA} \vdash \psi _i^0 \leftrightarrow \exists x \Bigl ( \bigl (\delta (x) \lor \mathrm {Prf}_T(\ulcorner \Box \psi _i^1\urcorner , x) \bigr ) \land \forall y < x \, \neg \mathrm {Prf}_T(\ulcorner \Box (\varphi _i \lor \psi _i^0)\urcorner , y) \Bigr )$
, -
•
 $\mathbf {PA} \vdash \psi _i^1 \phantom{\quad}\leftrightarrow \exists y \Bigl (\mathrm {Prf}_T(\ulcorner \Box (\varphi _i \lor \psi _i^0)\urcorner , y) \land \forall x \leq y \, \bigl (\neg \delta (x) \land \neg \mathrm {Prf}_T (\ulcorner \Box \psi _i^1\urcorner , x) \bigr ) \Bigr )$
.
$\mathbf {PA} \vdash \psi _i^1 \phantom{\quad}\leftrightarrow \exists y \Bigl (\mathrm {Prf}_T(\ulcorner \Box (\varphi _i \lor \psi _i^0)\urcorner , y) \land \forall x \leq y \, \bigl (\neg \delta (x) \land \neg \mathrm {Prf}_T (\ulcorner \Box \psi _i^1\urcorner , x) \bigr ) \Bigr )$
.
Then, for each i, we get
![]() $\mathbf {PA} \vdash \sigma \to \psi _i^0 \lor \psi _i^1$
. Hence, we have
$\mathbf {PA} \vdash \sigma \to \psi _i^0 \lor \psi _i^1$
. Hence, we have
By Theorem 2.8,
Hence,
On the other hand, for each i, we have
![]() $\mathbf {PA}(\mathbf {K}) \vdash \Box \varphi _i \to \Box (\varphi _i \lor \psi _i^0)$
. From our supposition, we obtain
$\mathbf {PA}(\mathbf {K}) \vdash \Box \varphi _i \to \Box (\varphi _i \lor \psi _i^0)$
. From our supposition, we obtain
By combining this with (2),
By
![]() $\mathrm {B}^{n+1}$
-
$\mathrm {B}^{n+1}$
-
![]() $\mathrm {DP}$
, we have
$\mathrm {DP}$
, we have
![]() $T \vdash \Box (\varphi _i \lor \psi _i^0)$
for some i or
$T \vdash \Box (\varphi _i \lor \psi _i^0)$
for some i or
![]() $T \vdash \Box (\psi _1^1 \land \cdots \land \psi _n^1)$
. If
$T \vdash \Box (\psi _1^1 \land \cdots \land \psi _n^1)$
. If
![]() $T \vdash \Box (\psi _1^1 \land \cdots \land \psi _n^1)$
, then
$T \vdash \Box (\psi _1^1 \land \cdots \land \psi _n^1)$
, then
![]() $T \vdash \Box \psi _i^1$
for each i.
$T \vdash \Box \psi _i^1$
for each i.
-
• If
 $T \vdash \Box (\varphi _i \lor \psi _i^0)$
and
$T \vdash \Box (\varphi _i \lor \psi _i^0)$
and
 $T \nvdash \Box \psi _i^1$
, then
$T \nvdash \Box \psi _i^1$
, then
 $\mathbb {N} \models \psi _i^1$
by the choice of
$\mathbb {N} \models \psi _i^1$
by the choice of
 $\psi _i^1$
because
$\psi _i^1$
because
 $\mathbb {N} \models \forall x \neg \delta (x)$
. Thus,
$\mathbb {N} \models \forall x \neg \delta (x)$
. Thus,
 $T \vdash \psi _i^1$
by
$T \vdash \psi _i^1$
by
 $\Sigma _1$
-completeness, and hence
$\Sigma _1$
-completeness, and hence
 $T \vdash \Box \psi _i^1$
. This is a contradiction.
$T \vdash \Box \psi _i^1$
. This is a contradiction. -
• If
 $T \vdash \Box \psi _i^1$
and
$T \vdash \Box \psi _i^1$
and
 $T \nvdash \Box (\varphi _i \lor \psi _i^0)$
, then
$T \nvdash \Box (\varphi _i \lor \psi _i^0)$
, then
 $\mathbb {N} \models \psi _i^0$
, and hence
$\mathbb {N} \models \psi _i^0$
, and hence
 $T \vdash \psi _i^0$
. Thus,
$T \vdash \psi _i^0$
. Thus,
 $T \vdash \varphi _i \lor \psi _i^0$
and hence
$T \vdash \varphi _i \lor \psi _i^0$
and hence
 $T \vdash \Box (\varphi _i \lor \psi _i^0)$
, a contradiction.
$T \vdash \Box (\varphi _i \lor \psi _i^0)$
, a contradiction.
We have shown that in either case, for some i, both
![]() $\Box (\varphi _i \lor \psi _i^0)$
and
$\Box (\varphi _i \lor \psi _i^0)$
and
![]() $\Box \psi _i^1$
are provable in T. Since
$\Box \psi _i^1$
are provable in T. Since
![]() $\mathbf {PA} \vdash \psi _i^1 \to \neg \psi _i^0$
, we have
$\mathbf {PA} \vdash \psi _i^1 \to \neg \psi _i^0$
, we have
![]() $T \vdash \Box \neg \psi _i^0$
for such an i. Therefore, we conclude
$T \vdash \Box \neg \psi _i^0$
for such an i. Therefore, we conclude
![]() $T \vdash \Box \varphi _i$
.
$T \vdash \Box \varphi _i$
.
From Propositions 3.11 and 4.16 and Lemma 4.19, we obtain the following proposition.
Proposition 4.20. Let T be any r.e. extension of
![]() $\mathbf {PA}(\mathbf {K})$
.
$\mathbf {PA}(\mathbf {K})$
.
-
1. If T has
 $\Delta (\mathrm {B})$
-
$\Delta (\mathrm {B})$
-
 $\mathrm {DP}$
, then T has
$\mathrm {DP}$
, then T has
 $(\Delta (\mathrm {B}), \Sigma _1)$
-
$(\Delta (\mathrm {B}), \Sigma _1)$
-
 $\mathrm {DP}$
.
$\mathrm {DP}$
. -
2. If T has
 $\mathrm {B}$
-
$\mathrm {B}$
-
 $\mathrm {DP}$
, then T has
$\mathrm {DP}$
, then T has
 $(\mathrm {B}, \Sigma _1)$
-
$(\mathrm {B}, \Sigma _1)$
-
 $\mathrm {DP}$
.
$\mathrm {DP}$
.
Proposition 4.21. Let T be any r.e. extension of
![]() $\mathbf {PA}(\mathbf {K})$
with
$\mathbf {PA}(\mathbf {K})$
with
![]() $T \nvdash \Box \bot $
. If T has
$T \nvdash \Box \bot $
. If T has
![]() $(\mathrm {B}, \Sigma _1)$
-
$(\mathrm {B}, \Sigma _1)$
-
![]() $\mathrm {DP}$
, then T is
$\mathrm {DP}$
, then T is
![]() $\Sigma _1$
-sound.
$\Sigma _1$
-sound.
Proof. We prove the contrapositive. Suppose that
![]() $T \nvdash \Box \bot $
and T is not
$T \nvdash \Box \bot $
and T is not
![]() $\Sigma _1$
-sound. Then, there exists a
$\Sigma _1$
-sound. Then, there exists a
![]() $\Delta _0$
formula
$\Delta _0$
formula
![]() $\delta (x)$
such that
$\delta (x)$
such that
![]() $T \vdash \exists x \delta (x)$
and
$T \vdash \exists x \delta (x)$
and
![]() $\mathbb {N} \models \forall x \neg \delta (x)$
. Let
$\mathbb {N} \models \forall x \neg \delta (x)$
. Let
![]() $\sigma _0$
and
$\sigma _0$
and
![]() $\sigma _1$
be
$\sigma _1$
be
![]() $\Sigma _1$
sentences satisfying the following equivalences:
$\Sigma _1$
sentences satisfying the following equivalences:
-
•
 $\mathbf {PA} \vdash \sigma _0 \leftrightarrow \exists x \Bigl ( \bigl (\delta (x) \lor \mathrm {Prf}_T(\ulcorner \sigma _1\urcorner , x) \bigr ) \land \forall y < x \, \neg \mathrm {Prf}_T(\ulcorner \Box \sigma _0\urcorner , y) \Bigr )$
.
$\mathbf {PA} \vdash \sigma _0 \leftrightarrow \exists x \Bigl ( \bigl (\delta (x) \lor \mathrm {Prf}_T(\ulcorner \sigma _1\urcorner , x) \bigr ) \land \forall y < x \, \neg \mathrm {Prf}_T(\ulcorner \Box \sigma _0\urcorner , y) \Bigr )$
. -
•
 $\mathbf {PA} \vdash \sigma _1 \leftrightarrow \exists y \Bigl (\mathrm {Prf}_T(\ulcorner \Box \sigma _0\urcorner , y) \land \forall x \leq y \, \bigl (\neg \delta (x) \land \neg \mathrm {Prf}_T(\ulcorner \sigma _1\urcorner , x) \bigr ) \Bigr )$
.
$\mathbf {PA} \vdash \sigma _1 \leftrightarrow \exists y \Bigl (\mathrm {Prf}_T(\ulcorner \Box \sigma _0\urcorner , y) \land \forall x \leq y \, \bigl (\neg \delta (x) \land \neg \mathrm {Prf}_T(\ulcorner \sigma _1\urcorner , x) \bigr ) \Bigr )$
.
Since
![]() $T \vdash \exists x \delta (x)$
, we have
$T \vdash \exists x \delta (x)$
, we have
![]() $T \vdash \sigma _0 \lor \sigma _1$
. Therefore,
$T \vdash \sigma _0 \lor \sigma _1$
. Therefore,
![]() $T \vdash (\Box \sigma _0) \lor \sigma _1$
by Theorem 2.8.
$T \vdash (\Box \sigma _0) \lor \sigma _1$
by Theorem 2.8.
Suppose, towards a contradiction, that
![]() $T \vdash \Box \sigma _0$
or
$T \vdash \Box \sigma _0$
or
![]() $T \vdash \sigma _1$
. Let p be the smallest T-proof of
$T \vdash \sigma _1$
. Let p be the smallest T-proof of
![]() $\Box \sigma _0$
or
$\Box \sigma _0$
or
![]() $\sigma _1$
. If p is a proof of
$\sigma _1$
. If p is a proof of
![]() $\Box \sigma _0$
, then
$\Box \sigma _0$
, then
![]() $\mathbb {N} \models \sigma _1$
by the choice of
$\mathbb {N} \models \sigma _1$
by the choice of
![]() $\sigma _1$
. Hence,
$\sigma _1$
. Hence,
![]() $T \vdash \sigma _1$
and thus
$T \vdash \sigma _1$
and thus
![]() $T \vdash \Box \sigma _1$
. Since
$T \vdash \Box \sigma _1$
. Since
![]() $T \vdash \sigma _0 \land \sigma _1 \to \bot $
, we have
$T \vdash \sigma _0 \land \sigma _1 \to \bot $
, we have
![]() $T \vdash \Box \bot $
because
$T \vdash \Box \bot $
because
![]() $T \vdash \Box \sigma _0 \land \Box \sigma _1$
. This is a contradiction. If p is a proof of
$T \vdash \Box \sigma _0 \land \Box \sigma _1$
. This is a contradiction. If p is a proof of
![]() $\sigma _1$
, then it is shown
$\sigma _1$
, then it is shown
![]() $T \vdash \sigma _0$
. This contradicts the consistency of T. Thus, we have shown that
$T \vdash \sigma _0$
. This contradicts the consistency of T. Thus, we have shown that
![]() $T \nvdash \Box \sigma _0$
and
$T \nvdash \Box \sigma _0$
and
![]() $T \nvdash \sigma _1$
. This means that T does not have
$T \nvdash \sigma _1$
. This means that T does not have
![]() $(\mathrm {B}, \Sigma _1)$
-
$(\mathrm {B}, \Sigma _1)$
-
![]() $\mathrm {DP}$
.
$\mathrm {DP}$
.
Proposition 4.22. Let T be any consistent r.e. extension of
![]() $\mathbf {PA}(\mathbf {K})$
with
$\mathbf {PA}(\mathbf {K})$
with
![]() $T \nvdash \Box \bot $
and let
$T \nvdash \Box \bot $
and let
![]() $\Gamma $
be a class of formulas with
$\Gamma $
be a class of formulas with
![]() $\mathrm {B} \subseteq \Gamma $
. If T has
$\mathrm {B} \subseteq \Gamma $
. If T has
![]() $(\Gamma , \Sigma _1)$
-
$(\Gamma , \Sigma _1)$
-
![]() $\mathrm {DP}$
, then T is
$\mathrm {DP}$
, then T is
![]() $\Gamma $
-
$\Gamma $
-
![]() $\mathrm {DC}$
.
$\mathrm {DC}$
.
Proof. Suppose that T has
![]() $(\Gamma , \Sigma _1)$
-
$(\Gamma , \Sigma _1)$
-
![]() $\mathrm {DP}$
. Let
$\mathrm {DP}$
. Let
![]() $\varphi $
be any
$\varphi $
be any
![]() $\Gamma $
sentence such that
$\Gamma $
sentence such that
![]() $T \vdash \varphi \lor \mathrm {Pr}_T(\ulcorner \varphi \urcorner )$
. By
$T \vdash \varphi \lor \mathrm {Pr}_T(\ulcorner \varphi \urcorner )$
. By
![]() $(\Gamma , \Sigma _1)$
-
$(\Gamma , \Sigma _1)$
-
![]() $\mathrm {DP}$
,
$\mathrm {DP}$
,
![]() $T \vdash \varphi $
or
$T \vdash \varphi $
or
![]() $T \vdash \mathrm {Pr}_T(\ulcorner \varphi \urcorner )$
. Since
$T \vdash \mathrm {Pr}_T(\ulcorner \varphi \urcorner )$
. Since
![]() $\mathrm {B} \subseteq \Gamma $
, by Proposition 4.21, T is
$\mathrm {B} \subseteq \Gamma $
, by Proposition 4.21, T is
![]() $\Sigma _1$
-sound. Thus, in either case, we obtain
$\Sigma _1$
-sound. Thus, in either case, we obtain
![]() $T \vdash \varphi $
.
$T \vdash \varphi $
.
The converse implication also holds when
![]() $\Gamma $
is
$\Gamma $
is
![]() $\mathrm {B}$
or
$\mathrm {B}$
or
![]() $\Delta (\mathrm {B})$
. In order to prove this, we generalize the Fixed Point Lemma to modal arithmetic. It is proved by repeating a well-known proof, and so we omit it (see [Reference Boolos1]).
$\Delta (\mathrm {B})$
. In order to prove this, we generalize the Fixed Point Lemma to modal arithmetic. It is proved by repeating a well-known proof, and so we omit it (see [Reference Boolos1]).
Lemma 4.23 (The Fixed Point Lemma)
For any
![]() $\mathcal {L}_A(\Box )$
-formulas
$\mathcal {L}_A(\Box )$
-formulas
![]() $\varphi _0(x_0, \ldots , x_{k-1})$
,
$\varphi _0(x_0, \ldots , x_{k-1})$
,
![]() $\ldots $
,
$\ldots $
,
![]() $\varphi _{k-1}(x_0, \ldots , x_{k-1})$
with only the free variables
$\varphi _{k-1}(x_0, \ldots , x_{k-1})$
with only the free variables
![]() $x_0, \ldots , x_{k-1}$
, we can effectively find
$x_0, \ldots , x_{k-1}$
, we can effectively find
![]() $\mathcal {L}_A(\Box )$
-sentences
$\mathcal {L}_A(\Box )$
-sentences
![]() $\psi _0, \ldots , \psi _{k-1}$
such that for each
$\psi _0, \ldots , \psi _{k-1}$
such that for each
![]() $i < k$
,
$i < k$
,
Moreover, for each
![]() $i < k$
, if
$i < k$
, if
![]() $\varphi _i(x_0, \ldots , x_{k-1})$
is a
$\varphi _i(x_0, \ldots , x_{k-1})$
is a
![]() $\Sigma (\mathrm {B})$
formula, then such a
$\Sigma (\mathrm {B})$
formula, then such a
![]() $\psi _i$
can be found as a
$\psi _i$
can be found as a
![]() $\Sigma (\mathrm {B})$
sentence.
$\Sigma (\mathrm {B})$
sentence.
Proposition 4.24. Let T be any r.e. extension of
![]() $\mathbf {PA}(\mathbf {K})$
.
$\mathbf {PA}(\mathbf {K})$
.
-
1. If T is
 $\Delta (\mathrm {B})$
-
$\Delta (\mathrm {B})$
-
 $\mathrm {DC}$
, then T has
$\mathrm {DC}$
, then T has
 $(\Delta (\mathrm {B}), \Sigma _1)$
-
$(\Delta (\mathrm {B}), \Sigma _1)$
-
 $\mathrm {DP}$
.
$\mathrm {DP}$
. -
2. If T is
 $\mathrm {B}$
-
$\mathrm {B}$
-
 $\mathrm {DC}$
, then T has
$\mathrm {DC}$
, then T has
 $(\mathrm {B}, \Sigma _1)$
-
$(\mathrm {B}, \Sigma _1)$
-
 $\mathrm {DP}$
.
$\mathrm {DP}$
.
Proof. We prove only Clause 1. Clause 2 is proved similarly. Suppose that T is
![]() $\Delta (\mathrm {B})$
-
$\Delta (\mathrm {B})$
-
![]() $\mathrm {DC}$
. Let
$\mathrm {DC}$
. Let
![]() $\varphi $
be any
$\varphi $
be any
![]() $\Delta (\mathrm {B})$
sentence and let
$\Delta (\mathrm {B})$
sentence and let
![]() $\delta (x)$
be any
$\delta (x)$
be any
![]() $\Delta _0$
formula such that
$\Delta _0$
formula such that
![]() $T \vdash \varphi \lor \exists x \delta (x)$
and
$T \vdash \varphi \lor \exists x \delta (x)$
and
![]() $T \nvdash \exists x \delta (x)$
. We would like to show
$T \nvdash \exists x \delta (x)$
. We would like to show
![]() $T \vdash \varphi $
. In this case,
$T \vdash \varphi $
. In this case,
![]() $\mathbb {N} \models \forall x \neg \delta (x)$
. By Proposition 3.11, we may assume that
$\mathbb {N} \models \forall x \neg \delta (x)$
. By Proposition 3.11, we may assume that
![]() $\varphi $
is of the form
$\varphi $
is of the form
![]() $\Box \psi _0 \lor \cdots \lor \Box \psi _{k-1}$
. By the Fixed Point Lemma, let
$\Box \psi _0 \lor \cdots \lor \Box \psi _{k-1}$
. By the Fixed Point Lemma, let
![]() $\xi _0, \ldots , \xi _{k-1}$
be
$\xi _0, \ldots , \xi _{k-1}$
be
![]() $\mathcal {L}_A(\Box )$
-sentences satisfying the following equivalences for all
$\mathcal {L}_A(\Box )$
-sentences satisfying the following equivalences for all
![]() $i < k$
:
$i < k$
:
Since
![]() $\mathbf {PA}_{\Box } \vdash \psi _i \to \xi _i$
, we have
$\mathbf {PA}_{\Box } \vdash \psi _i \to \xi _i$
, we have
![]() $\mathbf {PA}(\mathbf {K}) \vdash \Box \psi _i \to \Box \xi _i$
. Also,
$\mathbf {PA}(\mathbf {K}) \vdash \Box \psi _i \to \Box \xi _i$
. Also,
 $$ \begin{align*} \mathbf{PA}(\mathbf{K}) \vdash \exists x \delta(x) \land & \neg \mathrm{Pr}_T(\ulcorner\Box \xi_0 \lor \cdots \lor \Box \xi_{k-1}\urcorner) \\ & \ \ \ \to \exists x \bigl(\delta(x) \land \forall y < x \, \neg \mathrm{Prf}_T(\ulcorner\Box \xi_0 \lor \cdots \lor \Box \xi_{k-1}\urcorner, y) \bigr), \\ & \ \ \ \to \mathrm{Pr}_T \Bigl(\ulcorner\exists x \bigl(\delta(x) \land \forall y < x \, \neg \mathrm{Prf}_T(\ulcorner\Box \xi_0 \lor \cdots \lor \Box \xi_{k-1}\urcorner, y) \bigr)\urcorner \Bigr), \\ & \ \ \ \to \mathrm{Pr}_T(\ulcorner\xi_i\urcorner). \end{align*} $$
$$ \begin{align*} \mathbf{PA}(\mathbf{K}) \vdash \exists x \delta(x) \land & \neg \mathrm{Pr}_T(\ulcorner\Box \xi_0 \lor \cdots \lor \Box \xi_{k-1}\urcorner) \\ & \ \ \ \to \exists x \bigl(\delta(x) \land \forall y < x \, \neg \mathrm{Prf}_T(\ulcorner\Box \xi_0 \lor \cdots \lor \Box \xi_{k-1}\urcorner, y) \bigr), \\ & \ \ \ \to \mathrm{Pr}_T \Bigl(\ulcorner\exists x \bigl(\delta(x) \land \forall y < x \, \neg \mathrm{Prf}_T(\ulcorner\Box \xi_0 \lor \cdots \lor \Box \xi_{k-1}\urcorner, y) \bigr)\urcorner \Bigr), \\ & \ \ \ \to \mathrm{Pr}_T(\ulcorner\xi_i\urcorner). \end{align*} $$
Since
![]() $\mathbf {PA}(\mathbf {K}) \vdash \mathrm {Pr}_T(\ulcorner \xi _i\urcorner ) \to \mathrm {Pr}_T(\ulcorner \Box \xi _i\urcorner )$
because
$\mathbf {PA}(\mathbf {K}) \vdash \mathrm {Pr}_T(\ulcorner \xi _i\urcorner ) \to \mathrm {Pr}_T(\ulcorner \Box \xi _i\urcorner )$
because
![]() $\mathbf {PA}$
can prove that the consequences of T are closed under the rule Nec, we obtain
$\mathbf {PA}$
can prove that the consequences of T are closed under the rule Nec, we obtain
![]() $\mathbf {PA}(\mathbf {K}) \vdash \mathrm {Pr}_T(\ulcorner \xi _i\urcorner ) \to \mathrm {Pr}_T(\ulcorner \Box \xi _0 \lor \cdots \lor \Box \xi _{k-1}\urcorner )$
. Thus, we have
$\mathbf {PA}(\mathbf {K}) \vdash \mathrm {Pr}_T(\ulcorner \xi _i\urcorner ) \to \mathrm {Pr}_T(\ulcorner \Box \xi _0 \lor \cdots \lor \Box \xi _{k-1}\urcorner )$
. Thus, we have
and hence
Then, by combining this with our assumption that
![]() $T \vdash \Box \psi _0 \lor \cdots \lor \Box \psi _{k-1} \lor \exists x \delta (x)$
, we obtain
$T \vdash \Box \psi _0 \lor \cdots \lor \Box \psi _{k-1} \lor \exists x \delta (x)$
, we obtain
By
![]() $\Delta (\mathrm {B})$
-
$\Delta (\mathrm {B})$
-
![]() $\mathrm {DC}$
, we have
$\mathrm {DC}$
, we have
Since
this sentence is provable in
![]() $\mathbf {PA}(\mathbf {K})$
. Thus,
$\mathbf {PA}(\mathbf {K})$
. Thus,
Then, by the choice of
![]() $\xi _i$
,
$\xi _i$
,
![]() $\mathbf {PA}(\mathbf {K}) \vdash \xi _i \to \psi _i$
for each i. From (3), we conclude
$\mathbf {PA}(\mathbf {K}) \vdash \xi _i \to \psi _i$
for each i. From (3), we conclude
![]() $T \vdash \Box \psi _0 \lor \cdots \lor \Box \psi _{k-1}$
and hence
$T \vdash \Box \psi _0 \lor \cdots \lor \Box \psi _{k-1}$
and hence
![]() $T \vdash \varphi $
.
$T \vdash \varphi $
.
In the statements of Propositions 4.21 and 4.22, the condition “
![]() $T \nvdash \Box \bot $
” is assumed. On the other hand, for consistent theories T with
$T \nvdash \Box \bot $
” is assumed. On the other hand, for consistent theories T with
![]() $T \vdash \Box \bot $
, the situation changes. Indeed, every
$T \vdash \Box \bot $
, the situation changes. Indeed, every
![]() $\mathrm {B}$
formula is provable in such a theory T. Thus, T does not have
$\mathrm {B}$
formula is provable in such a theory T. Thus, T does not have
![]() $\mathrm {MDP}$
and
$\mathrm {MDP}$
and
![]() $\mathrm {MEP}$
. Also, every
$\mathrm {MEP}$
. Also, every
![]() $\Delta (\mathrm {B})$
formula is T-provably equivalent to some
$\Delta (\mathrm {B})$
formula is T-provably equivalent to some
![]() $\Delta _0$
formula. Moreover, every
$\Delta _0$
formula. Moreover, every
![]() $\Delta (\mathrm {B})$
sentence
$\Delta (\mathrm {B})$
sentence
![]() $\varphi $
is either provable or refutable in T. Therefore, we obtain the following proposition.
$\varphi $
is either provable or refutable in T. Therefore, we obtain the following proposition.
Proposition 4.25. Let T be any extension of
![]() $\mathbf {PA}(\mathbf {Verum})$
. Then, T has
$\mathbf {PA}(\mathbf {Verum})$
. Then, T has
![]() $\Delta (\mathrm {B})$
-
$\Delta (\mathrm {B})$
-
![]() $\mathrm {DP}$
,
$\mathrm {DP}$
,
![]() $(\Delta (\mathrm {B}), \Sigma _1)$
-
$(\Delta (\mathrm {B}), \Sigma _1)$
-
![]() $\mathrm {DP}$
, and
$\mathrm {DP}$
, and
![]() $\mathrm {B}$
-
$\mathrm {B}$
-
![]() $\mathrm {EP}$
. Also, T is
$\mathrm {EP}$
. Also, T is
![]() $\mathrm {B}$
-
$\mathrm {B}$
-
![]() $\mathrm {DC}$
.
$\mathrm {DC}$
.
From Propositions 4.22, 4.24, and 4.25, we have:
Corollary 4.26. Let T be any consistent r.e. extension of
![]() $\mathbf {PA}(\mathbf {K})$
.
$\mathbf {PA}(\mathbf {K})$
.
-
1. If
 $T \nvdash \Box \bot $
, then T has
$T \nvdash \Box \bot $
, then T has
 $(\Delta (\mathrm {B}), \Sigma _1)$
-
$(\Delta (\mathrm {B}), \Sigma _1)$
-
 $\mathrm {DP}$
if and only if T is
$\mathrm {DP}$
if and only if T is
 $\Delta (\mathrm {B})$
-
$\Delta (\mathrm {B})$
-
 $\mathrm {DC}$
.
$\mathrm {DC}$
. -
2. T has
 $(\mathrm {B}, \Sigma _1)$
-
$(\mathrm {B}, \Sigma _1)$
-
 $\mathrm {DP}$
if and only if T is
$\mathrm {DP}$
if and only if T is
 $\mathrm {B}$
-
$\mathrm {B}$
-
 $\mathrm {DC}$
.
$\mathrm {DC}$
.
For consistent r.e. extensions of
![]() $\mathbf {PA}(\mathbf {Verum})$
,
$\mathbf {PA}(\mathbf {Verum})$
,
![]() $\Delta (\mathrm {B})$
-
$\Delta (\mathrm {B})$
-
![]() $\mathrm {DC}$
is strictly weaker than
$\mathrm {DC}$
is strictly weaker than
![]() $\Sigma _1$
-soundness.
$\Sigma _1$
-soundness.
Proposition 4.27. Let T be any consistent r.e. extension of
![]() $\mathbf {PA}(\mathbf {Verum})$
. Then, the following are equivalent:
$\mathbf {PA}(\mathbf {Verum})$
. Then, the following are equivalent:
-
1. T is
 $\Delta (\mathrm {B})$
-
$\Delta (\mathrm {B})$
-
 $\mathrm {DC}$
.
$\mathrm {DC}$
. -
2.
 $T \nvdash \neg \mathrm {Con}_T$
.
$T \nvdash \neg \mathrm {Con}_T$
.
Proof.
![]() $(1 \Rightarrow 2)$
: Suppose that T is
$(1 \Rightarrow 2)$
: Suppose that T is
![]() $\Delta (\mathrm {B})$
-
$\Delta (\mathrm {B})$
-
![]() $\mathrm {DC}$
. Since
$\mathrm {DC}$
. Since
![]() $T \nvdash \bot $
, we obtain
$T \nvdash \bot $
, we obtain
![]() $T \nvdash \mathrm {Pr}_T(\ulcorner \bot \urcorner ) \lor \bot $
. Hence,
$T \nvdash \mathrm {Pr}_T(\ulcorner \bot \urcorner ) \lor \bot $
. Hence,
![]() $T \nvdash \neg \mathrm {Con}_T$
.
$T \nvdash \neg \mathrm {Con}_T$
.
![]() $(2 \Rightarrow 1)$
: Suppose
$(2 \Rightarrow 1)$
: Suppose
![]() $T \nvdash \neg \mathrm {Con}_T$
. Let
$T \nvdash \neg \mathrm {Con}_T$
. Let
![]() $\varphi $
be any
$\varphi $
be any
![]() $\Delta (\mathrm {B})$
sentence with
$\Delta (\mathrm {B})$
sentence with
![]() $T \vdash \mathrm {Pr}_T(\ulcorner \varphi \urcorner ) \lor \varphi $
. If
$T \vdash \mathrm {Pr}_T(\ulcorner \varphi \urcorner ) \lor \varphi $
. If
![]() $T \vdash \neg \varphi $
, then
$T \vdash \neg \varphi $
, then
![]() $\varphi $
is T-equivalent to
$\varphi $
is T-equivalent to
![]() $\bot $
. We have
$\bot $
. We have
![]() $T \vdash \mathrm {Pr}_T(\ulcorner \bot \urcorner ) \lor \bot $
, and so
$T \vdash \mathrm {Pr}_T(\ulcorner \bot \urcorner ) \lor \bot $
, and so
![]() $T \vdash \neg \mathrm {Con}_T$
. This is a contradiction. Therefore,
$T \vdash \neg \mathrm {Con}_T$
. This is a contradiction. Therefore,
![]() $T \vdash \varphi $
.
$T \vdash \varphi $
.
There are
![]() $\mathcal {L}_A$
-sound theories that do not have even
$\mathcal {L}_A$
-sound theories that do not have even
![]() $(\mathrm {B}, \Sigma _1)$
-
$(\mathrm {B}, \Sigma _1)$
-
![]() $\mathrm {DP}$
.
$\mathrm {DP}$
.
Proposition 4.28.
-
1.
 $\mathbf {PA}(\mathbf {Triv})$
does not have
$\mathbf {PA}(\mathbf {Triv})$
does not have
 $(\mathrm {B}, \Sigma _1)$
-
$(\mathrm {B}, \Sigma _1)$
-
 $\mathrm {DP}$
.
$\mathrm {DP}$
. -
2. Let T be any r.e. theory such that
 $\mathbf {PA}(\mathbf {Verum}) \vdash T \vdash \mathbf {PA}(\mathbf {K4})$
and let
$\mathbf {PA}(\mathbf {Verum}) \vdash T \vdash \mathbf {PA}(\mathbf {K4})$
and let
 $U : = T + \{\mathrm {Pr}_T(\ulcorner \Box \bot \urcorner ) \lor \Box \bot \}$
. If
$U : = T + \{\mathrm {Pr}_T(\ulcorner \Box \bot \urcorner ) \lor \Box \bot \}$
. If
 $T \nvdash \Box \bot $
, then U is
$T \nvdash \Box \bot $
, then U is
 $\mathcal {L}_A$
-sound but is not
$\mathcal {L}_A$
-sound but is not
 $\mathrm {B}$
-
$\mathrm {B}$
-
 $\mathrm {DC}$
.
$\mathrm {DC}$
.
Proof. 1. Let
![]() $\varphi $
be a
$\varphi $
be a
![]() $\Pi _1$
Gödel sentence of
$\Pi _1$
Gödel sentence of
![]() $\mathbf {PA}$
. Since
$\mathbf {PA}$
. Since
![]() $\mathbf {PA} \vdash \varphi \lor \neg \varphi $
, we have
$\mathbf {PA} \vdash \varphi \lor \neg \varphi $
, we have
![]() $\mathbf {PA}(\mathbf {Triv}) \vdash \Box \varphi \lor \neg \varphi $
. Since
$\mathbf {PA}(\mathbf {Triv}) \vdash \Box \varphi \lor \neg \varphi $
. Since
![]() $\mathbf {PA}(\mathbf {Triv})$
is a conservative extension of
$\mathbf {PA}(\mathbf {Triv})$
is a conservative extension of
![]() $\mathbf {PA}$
(Corollary 2.4),
$\mathbf {PA}$
(Corollary 2.4),
![]() $\mathbf {PA}(\mathbf {Triv}) \nvdash \varphi $
and
$\mathbf {PA}(\mathbf {Triv}) \nvdash \varphi $
and
![]() $\mathbf {PA}(\mathbf {Triv}) \nvdash \neg \varphi $
. Then,
$\mathbf {PA}(\mathbf {Triv}) \nvdash \neg \varphi $
. Then,
![]() $\mathbf {PA}(\mathbf {Triv}) \nvdash \Box \varphi $
and
$\mathbf {PA}(\mathbf {Triv}) \nvdash \Box \varphi $
and
![]() $\mathbf {PA}(\mathbf {Triv}) \nvdash \neg \varphi $
.
$\mathbf {PA}(\mathbf {Triv}) \nvdash \neg \varphi $
.
2. Since U is a subtheory of
![]() $\mathbf {PA}(\mathbf {Verum})$
, U is
$\mathbf {PA}(\mathbf {Verum})$
, U is
![]() $\mathcal {L}_A$
-sound by Corollary 2.7. Since
$\mathcal {L}_A$
-sound by Corollary 2.7. Since
![]() $U \vdash \mathrm {Pr}_{T}(\ulcorner \Box \bot \urcorner ) \lor \Box \bot $
, we have
$U \vdash \mathrm {Pr}_{T}(\ulcorner \Box \bot \urcorner ) \lor \Box \bot $
, we have
![]() $U \vdash \mathrm {Pr}_U(\ulcorner \Box \bot \urcorner ) \lor \Box \bot $
. Suppose, towards a contradiction,
$U \vdash \mathrm {Pr}_U(\ulcorner \Box \bot \urcorner ) \lor \Box \bot $
. Suppose, towards a contradiction,
![]() $U \vdash \Box \bot $
. Since
$U \vdash \Box \bot $
. Since
![]() $\mathrm {Pr}_{T}(\ulcorner \Box \bot \urcorner ) \lor \Box \bot $
is a
$\mathrm {Pr}_{T}(\ulcorner \Box \bot \urcorner ) \lor \Box \bot $
is a
![]() $\Sigma (\mathrm {B})$
sentence,
$\Sigma (\mathrm {B})$
sentence,
![]() $T \vdash \mathrm {Pr}_{T}(\ulcorner \Box \bot \urcorner ) \lor \Box \bot \to \Box \bot $
by the
$T \vdash \mathrm {Pr}_{T}(\ulcorner \Box \bot \urcorner ) \lor \Box \bot \to \Box \bot $
by the
![]() $\Sigma (\mathrm {B})$
-deduction theorem (Corollary 3.14). In particular,
$\Sigma (\mathrm {B})$
-deduction theorem (Corollary 3.14). In particular,
![]() $T \vdash \mathrm {Pr}_{T}(\ulcorner \Box \bot \urcorner ) \to \Box \bot $
. By Löb’s theorem,
$T \vdash \mathrm {Pr}_{T}(\ulcorner \Box \bot \urcorner ) \to \Box \bot $
. By Löb’s theorem,
![]() $T \vdash \Box \bot $
. This is a contradiction. Therefore,
$T \vdash \Box \bot $
. This is a contradiction. Therefore,
![]() $U \nvdash \Box \bot $
. Hence, U is not
$U \nvdash \Box \bot $
. Hence, U is not
![]() $\mathrm {B}$
-
$\mathrm {B}$
-
![]() $\mathrm {DC}$
.
$\mathrm {DC}$
.
5
 $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
 $\mathrm {DP}$
and related properties
$\mathrm {DP}$
and related properties
First of all, we consider the case that T proves
![]() $\Box \bot $
.
$\Box \bot $
.
Proposition 5.29. Let T be any consistent r.e. extension of
![]() $\mathbf {PA}(\mathbf {Verum})$
. Then, the following are equivalent:
$\mathbf {PA}(\mathbf {Verum})$
. Then, the following are equivalent:
-
1. T is
 $\Sigma _1$
-sound.
$\Sigma _1$
-sound. -
2. T has
 $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
 $\mathrm {DP}$
.
$\mathrm {DP}$
. -
3. T has
 $(\Sigma (\mathrm {B}), \Sigma _1)$
-
$(\Sigma (\mathrm {B}), \Sigma _1)$
-
 $\mathrm {DP}$
.
$\mathrm {DP}$
. -
4. T has
 $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
 $\mathrm {EP}$
.
$\mathrm {EP}$
. -
5. T has
 $\Delta (\mathrm {B})$
-
$\Delta (\mathrm {B})$
-
 $\mathrm {EP}$
.
$\mathrm {EP}$
. -
6. T is
 $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
 $\mathrm {DC}$
.
$\mathrm {DC}$
.
Proof. Since every
![]() $\Sigma (\mathrm {B})$
(resp.
$\Sigma (\mathrm {B})$
(resp.
![]() $\Delta (\mathrm {B})$
) formula is T-provably equivalent to some
$\Delta (\mathrm {B})$
) formula is T-provably equivalent to some
![]() $\Sigma _1$
(resp.
$\Sigma _1$
(resp.
![]() $\Delta _0$
) formula, we have
$\Delta _0$
) formula, we have
![]() $(2 \Leftrightarrow 3)$
. Also by Guaspari’s theorem [Reference Guaspari10] on the equivalence of the
$(2 \Leftrightarrow 3)$
. Also by Guaspari’s theorem [Reference Guaspari10] on the equivalence of the
![]() $\Sigma _1$
-soundness and
$\Sigma _1$
-soundness and
![]() $\Sigma _1$
-
$\Sigma _1$
-
![]() $\mathrm {DP}$
, the equivalence
$\mathrm {DP}$
, the equivalence
![]() $(1 \Leftrightarrow 2)$
holds. Moreover, since the implications “
$(1 \Leftrightarrow 2)$
holds. Moreover, since the implications “
![]() $\Sigma _1$
-sound
$\Sigma _1$
-sound
![]() $\Rightarrow \Sigma _1$
-
$\Rightarrow \Sigma _1$
-
![]() $\mathrm {EP}$
,” “
$\mathrm {EP}$
,” “
![]() $\Sigma _1$
-
$\Sigma _1$
-
![]() $\mathrm {EP} \Rightarrow \Delta _0$
-
$\mathrm {EP} \Rightarrow \Delta _0$
-
![]() $\mathrm {EP}$
,” and “
$\mathrm {EP}$
,” and “
![]() $\Delta _0$
-
$\Delta _0$
-
![]() $\mathrm {EP} \Rightarrow \Sigma _1$
-sound” are easily verified, we obtain that Clauses 1, 4, and 5 are pairwise equivalent. Finally, since the equivalence of the
$\mathrm {EP} \Rightarrow \Sigma _1$
-sound” are easily verified, we obtain that Clauses 1, 4, and 5 are pairwise equivalent. Finally, since the equivalence of the
![]() $\Sigma _1$
-soundness and
$\Sigma _1$
-soundness and
![]() $\Sigma _1$
-
$\Sigma _1$
-
![]() $\mathrm {DC}$
is shown in [Reference Kurahashi15], we get
$\mathrm {DC}$
is shown in [Reference Kurahashi15], we get
![]() $(1 \Leftrightarrow 6)$
.
$(1 \Leftrightarrow 6)$
.
Corollary 5.30.
![]() $\mathbf {PA}(\mathbf {Verum})$
has
$\mathbf {PA}(\mathbf {Verum})$
has
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {EP}$
but does not have
$\mathrm {EP}$
but does not have
![]() $\mathrm {MDP}$
.
$\mathrm {MDP}$
.
Proof. Since
![]() $\mathbf {PA}(\mathbf {Verum})$
is
$\mathbf {PA}(\mathbf {Verum})$
is
![]() $\Sigma _1$
-sound by Corollary 2.7,
$\Sigma _1$
-sound by Corollary 2.7,
![]() $\mathbf {PA}(\mathbf {Verum})$
has
$\mathbf {PA}(\mathbf {Verum})$
has
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {EP}$
. On the other hand,
$\mathrm {EP}$
. On the other hand,
![]() $\mathbf {PA}(\mathbf {Verum}) \vdash \Box \bot $
and
$\mathbf {PA}(\mathbf {Verum}) \vdash \Box \bot $
and
![]() $\mathbf {PA}(\mathbf {Verum}) \nvdash \bot $
, and thus
$\mathbf {PA}(\mathbf {Verum}) \nvdash \bot $
, and thus
![]() $\mathbf {PA}(\mathbf {Verum})$
does not have
$\mathbf {PA}(\mathbf {Verum})$
does not have
![]() $\mathrm {MDP}$
.
$\mathrm {MDP}$
.
We then discuss theories in which
![]() $\Box \bot $
is not necessarily provable. Unlike the cases of
$\Box \bot $
is not necessarily provable. Unlike the cases of
![]() $\Delta (\mathrm {B})$
and
$\Delta (\mathrm {B})$
and
![]() $\mathrm {B}$
(Proposition 4.20),
$\mathrm {B}$
(Proposition 4.20),
![]() $(\Sigma (\mathrm {B}), \Sigma _1)$
-
$(\Sigma (\mathrm {B}), \Sigma _1)$
-
![]() $\mathrm {DP}$
directly follows from
$\mathrm {DP}$
directly follows from
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {DP}$
because
$\mathrm {DP}$
because
![]() $\Sigma _1 \subseteq \Sigma (\mathrm {B})$
. Also, as in the cases of
$\Sigma _1 \subseteq \Sigma (\mathrm {B})$
. Also, as in the cases of
![]() $\Delta (\mathrm {B})$
and
$\Delta (\mathrm {B})$
and
![]() $\mathrm {B}$
(Proposition 4.24), we obtain the following proposition.
$\mathrm {B}$
(Proposition 4.24), we obtain the following proposition.
Proposition 5.31. Let T be any r.e.
![]() $\mathcal {L}_A(\Box )$
-theory extending
$\mathcal {L}_A(\Box )$
-theory extending
![]() $\mathbf {PA}$
. If T is
$\mathbf {PA}$
. If T is
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {DC}$
, then T has
$\mathrm {DC}$
, then T has
![]() $(\Sigma (\mathrm {B}), \Sigma _1)$
-
$(\Sigma (\mathrm {B}), \Sigma _1)$
-
![]() $\mathrm {DP}$
.
$\mathrm {DP}$
.
Proof. Suppose that T is
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {DC}$
. Let
$\mathrm {DC}$
. Let
![]() $\varphi $
be any
$\varphi $
be any
![]() $\Sigma (\mathrm {B})$
sentence and let
$\Sigma (\mathrm {B})$
sentence and let
![]() $\delta (x)$
be any
$\delta (x)$
be any
![]() $\Delta _0$
formula such that
$\Delta _0$
formula such that
![]() $T \vdash \varphi \lor \exists x \delta (x)$
and
$T \vdash \varphi \lor \exists x \delta (x)$
and
![]() $T \nvdash \exists x \delta (x)$
. We would like to show
$T \nvdash \exists x \delta (x)$
. We would like to show
![]() $T \vdash \varphi $
. In this case,
$T \vdash \varphi $
. In this case,
![]() $\mathbb {N} \models \forall x \neg \delta (x)$
. Let
$\mathbb {N} \models \forall x \neg \delta (x)$
. Let
![]() $\sigma $
be a
$\sigma $
be a
![]() $\Sigma _1$
sentence satisfying
$\Sigma _1$
sentence satisfying
Since T is an extension of
![]() $\mathbf {PA}$
and
$\mathbf {PA}$
and
![]() $\sigma $
is
$\sigma $
is
![]() $\Sigma _1$
, we have
$\Sigma _1$
, we have
![]() $\mathbf {PA} \vdash \sigma \to \mathrm {Pr}_T(\ulcorner \sigma \urcorner )$
, and hence
$\mathbf {PA} \vdash \sigma \to \mathrm {Pr}_T(\ulcorner \sigma \urcorner )$
, and hence
![]() $\mathbf {PA} \vdash \sigma \to \mathrm {Pr}_T(\ulcorner \varphi \lor \sigma \urcorner )$
. By the equivalence (4), we obtain
$\mathbf {PA} \vdash \sigma \to \mathrm {Pr}_T(\ulcorner \varphi \lor \sigma \urcorner )$
. By the equivalence (4), we obtain
It follows
![]() $\mathbf {PA} \vdash \exists x \delta (x) \land \neg \mathrm {Prf}_T(\ulcorner \varphi \lor \sigma \urcorner ) \to \mathrm {Pr}_T(\ulcorner \varphi \lor \sigma \urcorner )$
, and hence
$\mathbf {PA} \vdash \exists x \delta (x) \land \neg \mathrm {Prf}_T(\ulcorner \varphi \lor \sigma \urcorner ) \to \mathrm {Pr}_T(\ulcorner \varphi \lor \sigma \urcorner )$
, and hence
Since
![]() $T \vdash \varphi \lor \exists x \delta (x)$
, we obtain
$T \vdash \varphi \lor \exists x \delta (x)$
, we obtain
![]() $T \vdash (\varphi \lor \sigma ) \lor \mathrm {Pr}_T(\ulcorner \varphi \lor \sigma \urcorner )$
. Since
$T \vdash (\varphi \lor \sigma ) \lor \mathrm {Pr}_T(\ulcorner \varphi \lor \sigma \urcorner )$
. Since
![]() $\varphi \lor \sigma $
is a
$\varphi \lor \sigma $
is a
![]() $\Sigma (\mathrm {B})$
sentence, by
$\Sigma (\mathrm {B})$
sentence, by
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {DC}$
, we have
$\mathrm {DC}$
, we have
![]() $T \vdash \varphi \lor \sigma $
. Since
$T \vdash \varphi \lor \sigma $
. Since
![]() $\mathbb {N} \models \forall x \neg \delta (x)$
,
$\mathbb {N} \models \forall x \neg \delta (x)$
,
![]() $\mathbb {N} \models \exists y \bigl (\mathrm {Prf}_T(\ulcorner \varphi \lor \sigma \urcorner , y) \land \forall x \leq y \, \neg \delta (x) \bigr )$
and this is provable in T. Then,
$\mathbb {N} \models \exists y \bigl (\mathrm {Prf}_T(\ulcorner \varphi \lor \sigma \urcorner , y) \land \forall x \leq y \, \neg \delta (x) \bigr )$
and this is provable in T. Then,
![]() $T \vdash \neg \sigma $
, and thus
$T \vdash \neg \sigma $
, and thus
![]() $T \vdash \varphi $
.
$T \vdash \varphi $
.
From Propositions 4.22, 5.29, and 5.31, we obtain the following corollary.
Corollary 5.32. For any r.e. extension T of
![]() $\mathbf {PA}(\mathbf {K})$
, T has
$\mathbf {PA}(\mathbf {K})$
, T has
![]() $(\Sigma (\mathrm {B}), \Sigma _1)$
-
$(\Sigma (\mathrm {B}), \Sigma _1)$
-
![]() $\mathrm {DP}$
if and only if T is
$\mathrm {DP}$
if and only if T is
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {DC}$
.
$\mathrm {DC}$
.
Before proving our main theorem of this section, we prepare some notations and lemmas.
Definition 5.33. For each
![]() $\Sigma (\mathrm {B})$
formula
$\Sigma (\mathrm {B})$
formula
![]() $\varphi $
, we define the
$\varphi $
, we define the
![]() $\mathcal {L}_A(\Box )$
-formula
$\mathcal {L}_A(\Box )$
-formula
![]() $\varphi ^-$
inductively as follows:
$\varphi ^-$
inductively as follows:
-
1. If
 $\varphi $
is
$\varphi $
is
 $\Sigma _1$
, then
$\Sigma _1$
, then
 $\varphi ^- : \equiv \varphi $
.
$\varphi ^- : \equiv \varphi $
. -
2. If
 $\varphi $
is of the form
$\varphi $
is of the form
 $\Box \psi $
, then
$\Box \psi $
, then
 $\varphi ^- : \equiv \psi $
.
$\varphi ^- : \equiv \psi $
. -
3. Otherwise if
 $\varphi $
is of the form
$\varphi $
is of the form
 $\psi \land \sigma $
,
$\psi \land \sigma $
,
 $\psi \lor \sigma $
,
$\psi \lor \sigma $
,
 $\exists x \psi $
or
$\exists x \psi $
or
 $\forall x < t\, \psi $
, then
$\forall x < t\, \psi $
, then
 $\varphi ^-$
is respectively
$\varphi ^-$
is respectively
 $\psi ^- \land \sigma ^-$
,
$\psi ^- \land \sigma ^-$
,
 $\psi ^- \lor \sigma ^-$
,
$\psi ^- \lor \sigma ^-$
,
 $\exists x \psi ^-$
or
$\exists x \psi ^-$
or
 $\forall x < t\, \psi ^-$
.
$\forall x < t\, \psi ^-$
.
The operation
![]() $(\cdot )^-$
removes the outermost
$(\cdot )^-$
removes the outermost
![]() $\Box $
of nested occurrences of
$\Box $
of nested occurrences of
![]() $\Box $
’s in the formula. For example,
$\Box $
’s in the formula. For example,
![]() $(\Box \Box \varphi \lor \Box \psi )^-$
is
$(\Box \Box \varphi \lor \Box \psi )^-$
is
![]() $\Box \varphi \lor \psi $
. The following lemma is a strengthening of Theorem 2.8.
$\Box \varphi \lor \psi $
. The following lemma is a strengthening of Theorem 2.8.
Lemma 5.34. For any
![]() $\Sigma (\mathrm {B})$
formula
$\Sigma (\mathrm {B})$
formula
![]() $\varphi $
,
$\varphi $
,
![]() $\mathbf {PA}(\mathbf {K}) \vdash \varphi \to \Box (\varphi ^-)$
.
$\mathbf {PA}(\mathbf {K}) \vdash \varphi \to \Box (\varphi ^-)$
.
Proof. This lemma is proved by induction on the construction of
![]() $\varphi $
as in the proof of Theorem 3.13. Notice that if
$\varphi $
as in the proof of Theorem 3.13. Notice that if
![]() $\varphi $
is of the form
$\varphi $
is of the form
![]() $\Box \psi $
, then
$\Box \psi $
, then
![]() $\varphi ^- \equiv \psi $
and thus
$\varphi ^- \equiv \psi $
and thus
![]() $\mathbf {PA}(\mathbf {K}) \vdash \varphi \to \Box (\varphi ^-)$
holds.
$\mathbf {PA}(\mathbf {K}) \vdash \varphi \to \Box (\varphi ^-)$
holds.
Definition 5.35. For each
![]() $\Delta (\mathrm {B})$
formula
$\Delta (\mathrm {B})$
formula
![]() $\varphi (\vec {x})$
, we define the
$\varphi (\vec {x})$
, we define the
![]() $\Delta (\mathrm {B})$
formula
$\Delta (\mathrm {B})$
formula
![]() $\varphi ^*(\vec {x}, \vec {v})$
with zero or more additional free variables
$\varphi ^*(\vec {x}, \vec {v})$
with zero or more additional free variables
![]() $\vec {v}$
which do not occur in
$\vec {v}$
which do not occur in
![]() $\varphi (\vec {x})$
inductively as follows:
$\varphi (\vec {x})$
inductively as follows:
-
1. If
 $\varphi (\vec {x})$
is either
$\varphi (\vec {x})$
is either
 $\Delta _0$
or of the form
$\Delta _0$
or of the form
 $\Box \psi (\vec {x})$
, then
$\Box \psi (\vec {x})$
, then
 $\varphi ^*(\vec {x}) : \equiv \varphi (\vec {x})$
.
$\varphi ^*(\vec {x}) : \equiv \varphi (\vec {x})$
. -
2. Otherwise if
 $\varphi (\vec {x})$
is of the form
$\varphi (\vec {x})$
is of the form
 $\psi (\vec {x}) \land \sigma (\vec {x})$
, then
$\psi (\vec {x}) \land \sigma (\vec {x})$
, then
 $\varphi ^*(\vec {x}, \vec {u}, \vec {v}) : \equiv \psi ^*(\vec {x}, \vec {u}) \land \sigma ^*(\vec {x}, \vec {v})$
where
$\varphi ^*(\vec {x}, \vec {u}, \vec {v}) : \equiv \psi ^*(\vec {x}, \vec {u}) \land \sigma ^*(\vec {x}, \vec {v})$
where
 $\vec {u}$
and
$\vec {u}$
and
 $\vec {v}$
are pairwise disjoint.
$\vec {v}$
are pairwise disjoint. -
3. Otherwise if
 $\varphi (\vec {x})$
is of the form
$\varphi (\vec {x})$
is of the form
 $\psi (\vec {x}) \lor \sigma (\vec {x})$
, then
$\psi (\vec {x}) \lor \sigma (\vec {x})$
, then  $$\begin{align*}\varphi^*(\vec{x}, \vec{u}, \vec{v}, w) : \equiv \Bigl[ \bigl(w = 0 \land \psi^*(\vec{x}, \vec{u}) \bigr) \lor \bigl(w \neq 0 \land \sigma^*(\vec{x}, \vec{v}) \bigr) \Bigr], \end{align*}$$
$$\begin{align*}\varphi^*(\vec{x}, \vec{u}, \vec{v}, w) : \equiv \Bigl[ \bigl(w = 0 \land \psi^*(\vec{x}, \vec{u}) \bigr) \lor \bigl(w \neq 0 \land \sigma^*(\vec{x}, \vec{v}) \bigr) \Bigr], \end{align*}$$
where
 $\vec {u}$
,
$\vec {u}$
,
 $\vec {v}$
, and w are pairwise disjoint.
$\vec {v}$
, and w are pairwise disjoint. -
4. Otherwise if
 $\varphi (\vec {x})$
is of the form
$\varphi (\vec {x})$
is of the form
 $\forall y < t\, \psi (\vec {x}, y)$
, then
$\forall y < t\, \psi (\vec {x}, y)$
, then
 $\varphi ^*(\vec {x}, \vec {v}) : \equiv \forall y < t\, \psi ^*(\vec {x}, y, \vec {v})$
.
$\varphi ^*(\vec {x}, \vec {v}) : \equiv \forall y < t\, \psi ^*(\vec {x}, y, \vec {v})$
. -
5. Otherwise if
 $\varphi (\vec {x})$
is of the form
$\varphi (\vec {x})$
is of the form
 $\exists y < t\, \psi (\vec {x}, y)$
, then
$\exists y < t\, \psi (\vec {x}, y)$
, then
 $\varphi ^*(\vec {x}, \vec {v}, w)$
is the formula
$\varphi ^*(\vec {x}, \vec {v}, w)$
is the formula
 $\exists y < t\, (y = w \land \psi ^*(\vec {x}, y, \vec {v}))$
.
$\exists y < t\, (y = w \land \psi ^*(\vec {x}, y, \vec {v}))$
.
From the definition, we can easily prove the following lemma by induction on the construction of
![]() $\varphi (\vec {x}) \in \Delta (\mathrm {B})$
.
$\varphi (\vec {x}) \in \Delta (\mathrm {B})$
.
Lemma 5.36. For any
![]() $\Delta (\mathrm {B})$
formula
$\Delta (\mathrm {B})$
formula
![]() $\varphi (\vec {x})$
,
$\varphi (\vec {x})$
,
![]() $\mathbf {PA}_{\Box } \vdash \varphi (\vec {x}) \leftrightarrow \exists \vec {v} \varphi ^*(\vec {x}, \vec {v})$
.
$\mathbf {PA}_{\Box } \vdash \varphi (\vec {x}) \leftrightarrow \exists \vec {v} \varphi ^*(\vec {x}, \vec {v})$
.
The following lemma is an important feature of our two transformations
![]() $-$
and
$-$
and
![]() $*$
.
$*$
.
Lemma 5.37. Let T be any r.e. extension of
![]() $\mathbf {PA}(\mathbf {K})$
such that
$\mathbf {PA}(\mathbf {K})$
such that
![]() $T \nvdash \Box \bot $
. For any
$T \nvdash \Box \bot $
. For any
![]() $\Delta (\mathrm {B})$
sentence
$\Delta (\mathrm {B})$
sentence
![]() $\varphi $
, if there exist numbers
$\varphi $
, if there exist numbers
![]() $\vec {p}$
such that
$\vec {p}$
such that
![]() $T \vdash \Box (\varphi ^*)^-(\vec {\overline {p}})$
, then
$T \vdash \Box (\varphi ^*)^-(\vec {\overline {p}})$
, then
![]() $T \vdash \varphi $
.
$T \vdash \varphi $
.
Proof. We prove the lemma by induction on the construction of
![]() $\varphi $
.
$\varphi $
.
-
• If
 $\varphi $
is a
$\varphi $
is a
 $\Delta _0$
sentence, then
$\Delta _0$
sentence, then
 $(\varphi ^*)^- \equiv \varphi ^- \equiv \varphi $
. Suppose
$(\varphi ^*)^- \equiv \varphi ^- \equiv \varphi $
. Suppose
 $T \vdash \Box (\varphi ^*)^-$
, i.e.,
$T \vdash \Box (\varphi ^*)^-$
, i.e.,
 $T \vdash \Box \varphi $
. If
$T \vdash \Box \varphi $
. If
 $\mathbb {N} \models \neg \varphi $
, then
$\mathbb {N} \models \neg \varphi $
, then
 $T \vdash \neg \varphi $
and
$T \vdash \neg \varphi $
and
 $T \vdash \Box \neg \varphi $
. We have
$T \vdash \Box \neg \varphi $
. We have
 $T \vdash \Box \bot $
, a contradiction. Hence,
$T \vdash \Box \bot $
, a contradiction. Hence,
 $\mathbb {N} \models \varphi $
. We conclude
$\mathbb {N} \models \varphi $
. We conclude
 $T \vdash \varphi $
.
$T \vdash \varphi $
. -
• If
 $\varphi $
is of the form
$\varphi $
is of the form
 $\Box \psi $
, then
$\Box \psi $
, then
 $(\varphi ^*)^- \equiv (\Box \psi )^- \equiv \psi $
. Suppose
$(\varphi ^*)^- \equiv (\Box \psi )^- \equiv \psi $
. Suppose
 $T \vdash \Box (\varphi ^*)^-$
. Then,
$T \vdash \Box (\varphi ^*)^-$
. Then,
 $T \vdash \varphi $
.
$T \vdash \varphi $
. -
• If
 $\varphi $
is of the form
$\varphi $
is of the form
 $\psi \land \sigma $
, then
$\psi \land \sigma $
, then
 $(\varphi ^*)^-(\vec {u}, \vec {v}) \equiv (\psi ^*)^-(\vec {u}) \land (\sigma ^*)^-(\vec {v})$
. Suppose
$(\varphi ^*)^-(\vec {u}, \vec {v}) \equiv (\psi ^*)^-(\vec {u}) \land (\sigma ^*)^-(\vec {v})$
. Suppose
 $T \vdash \Box (\varphi ^*)^-(\vec {\overline {p}}, \vec {\overline {q}})$
. Then,
$T \vdash \Box (\varphi ^*)^-(\vec {\overline {p}}, \vec {\overline {q}})$
. Then,
 $T \vdash \Box (\psi ^*)^-(\vec {\overline {p}})$
and
$T \vdash \Box (\psi ^*)^-(\vec {\overline {p}})$
and
 $T \vdash \Box (\sigma ^*)^-(\vec {\overline {q}})$
. By the induction hypothesis,
$T \vdash \Box (\sigma ^*)^-(\vec {\overline {q}})$
. By the induction hypothesis,
 $T \vdash \psi $
and
$T \vdash \psi $
and
 $T \vdash \sigma $
. We conclude
$T \vdash \sigma $
. We conclude
 $T \vdash \varphi $
.
$T \vdash \varphi $
. -
• If
 $\varphi $
is of the form
$\varphi $
is of the form
 $\psi \lor \sigma $
, then Suppose
$\psi \lor \sigma $
, then Suppose $$\begin{align*}(\varphi^*)^-(\vec{u}, \vec{v}, w) \equiv \Bigl[ \bigl(w = 0 \land (\psi^*)^-(\vec{u}) \bigr) \lor \bigl(w \neq 0 \land (\sigma^*)^-(\vec{v}) \bigr) \Bigr]. \end{align*}$$
$$\begin{align*}(\varphi^*)^-(\vec{u}, \vec{v}, w) \equiv \Bigl[ \bigl(w = 0 \land (\psi^*)^-(\vec{u}) \bigr) \lor \bigl(w \neq 0 \land (\sigma^*)^-(\vec{v}) \bigr) \Bigr]. \end{align*}$$
 $T \vdash \Box (\varphi ^*)^-(\vec {\overline {p}}, \vec {\overline {q}}, \overline {r})$
. Then, If
$T \vdash \Box (\varphi ^*)^-(\vec {\overline {p}}, \vec {\overline {q}}, \overline {r})$
. Then, If $$\begin{align*}T \vdash \Box \Bigl[ \bigl(\overline{r} = 0 \land (\psi^*)^-(\vec{\overline{p}}) \bigr) \lor \bigl(\overline{r} \neq 0 \land (\sigma^*)^-(\vec{\overline{q}}) \bigr) \Bigr]. \end{align*}$$
$$\begin{align*}T \vdash \Box \Bigl[ \bigl(\overline{r} = 0 \land (\psi^*)^-(\vec{\overline{p}}) \bigr) \lor \bigl(\overline{r} \neq 0 \land (\sigma^*)^-(\vec{\overline{q}}) \bigr) \Bigr]. \end{align*}$$
 $r = 0$
, then
$r = 0$
, then
 $T \vdash \Box (\psi ^*)^-(\vec {\overline {p}})$
. By the induction hypothesis,
$T \vdash \Box (\psi ^*)^-(\vec {\overline {p}})$
. By the induction hypothesis,
 $T \vdash \psi $
. If
$T \vdash \psi $
. If
 $r \neq 0$
, then
$r \neq 0$
, then
 $T \vdash \Box (\sigma ^*)^-(\vec {\overline {q}})$
. By the induction hypothesis,
$T \vdash \Box (\sigma ^*)^-(\vec {\overline {q}})$
. By the induction hypothesis,
 $T \vdash \sigma $
. In either case,
$T \vdash \sigma $
. In either case,
 $T \vdash \varphi $
.
$T \vdash \varphi $
.
-
• If
 $\varphi $
is of the form
$\varphi $
is of the form
 $\forall x < t\, \psi (x)$
for some
$\forall x < t\, \psi (x)$
for some
 $\mathcal {L}_A$
-term
$\mathcal {L}_A$
-term
 $t$
, then
$t$
, then
 $(\varphi ^*)^-(\vec {v})$
is the formula
$(\varphi ^*)^-(\vec {v})$
is the formula
 $\forall x < t\, (\psi ^*)^-(\vec {v}, x)$
. Since
$\forall x < t\, (\psi ^*)^-(\vec {v}, x)$
. Since
 $\varphi $
is a sentence,
$\varphi $
is a sentence,
 $t$
is a closed term. Let
$t$
is a closed term. Let
 $k$
be the value of the term
$k$
be the value of the term
 $t$
and suppose
$t$
and suppose
 $T \vdash \Box (\varphi ^*)^-(\vec {\overline {p}})$
. Then, for all
$T \vdash \Box (\varphi ^*)^-(\vec {\overline {p}})$
. Then, for all
 $n < k$
,
$n < k$
,
 $T \vdash \Box (\psi ^*)^-(\vec {\overline {p}}, \overline {n})$
. By the induction hypothesis,
$T \vdash \Box (\psi ^*)^-(\vec {\overline {p}}, \overline {n})$
. By the induction hypothesis,
 $T \vdash \psi (\overline {n})$
. We obtain
$T \vdash \psi (\overline {n})$
. We obtain
 $T \vdash \varphi $
.
$T \vdash \varphi $
. -
• If
 $\varphi $
is of the form
$\varphi $
is of the form
 $\exists x < t\, \psi (x)$
for some closed term
$\exists x < t\, \psi (x)$
for some closed term
 $t$
, then Suppose
$t$
, then Suppose $$\begin{align*}(\varphi^*)^-(\vec{v}, w) \equiv \exists x < t \bigl(x = w \land (\psi^*)^-(\vec{v}, x) \bigr). \end{align*}$$
$$\begin{align*}(\varphi^*)^-(\vec{v}, w) \equiv \exists x < t \bigl(x = w \land (\psi^*)^-(\vec{v}, x) \bigr). \end{align*}$$
 $T \vdash \Box (\varphi ^*)^-(\vec {\overline {p}}, \overline {q})$
. Then,
$T \vdash \Box (\varphi ^*)^-(\vec {\overline {p}}, \overline {q})$
. Then,
 $T \vdash \Box \exists x < t \bigl (x = \overline {q} \land (\psi ^*)^-(\vec {\overline {p}}, x) \bigr )$
. Since
$T \vdash \Box \exists x < t \bigl (x = \overline {q} \land (\psi ^*)^-(\vec {\overline {p}}, x) \bigr )$
. Since
 $T \nvdash \Box \bot $
, the value of
$T \nvdash \Box \bot $
, the value of
 $t$
is larger than q. Since
$t$
is larger than q. Since
 $T \vdash \Box (\psi ^*)^-(\vec {\overline {p}}, \overline {q})$
, by the induction hypothesis,
$T \vdash \Box (\psi ^*)^-(\vec {\overline {p}}, \overline {q})$
, by the induction hypothesis,
 $T \vdash \psi (\overline {q})$
. Then,
$T \vdash \psi (\overline {q})$
. Then,
 $T \vdash \exists x < t\, \psi (x)$
, that is,
$T \vdash \exists x < t\, \psi (x)$
, that is,
 $T \vdash \varphi $
.
$T \vdash \varphi $
.
We are ready to prove our main theorem of this section.
Theorem 5.38. Let T be any r.e. extension of
![]() $\mathbf {PA}(\mathbf {K})$
such that
$\mathbf {PA}(\mathbf {K})$
such that
![]() $T \nvdash \Box \bot $
. Then, the following are equivalent:
$T \nvdash \Box \bot $
. Then, the following are equivalent:
-
1. T has
 $\Delta (\mathrm {B})$
-
$\Delta (\mathrm {B})$
-
 $\mathrm {DP}$
and
$\mathrm {DP}$
and
 $(\Sigma (\mathrm {B}), \Sigma _1)$
-
$(\Sigma (\mathrm {B}), \Sigma _1)$
-
 $\mathrm {DP}$
.
$\mathrm {DP}$
. -
2. T has
 $\mathrm {B}$
-
$\mathrm {B}$
-
 $\mathrm {EP}$
.
$\mathrm {EP}$
. -
3. T has
 $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
 $\mathrm {EP}$
.
$\mathrm {EP}$
. -
4. T has
 $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
 $\mathrm {DP}$
.
$\mathrm {DP}$
.
Proof.
![]() $(1 \Rightarrow 2)$
: Let
$(1 \Rightarrow 2)$
: Let
![]() $\varphi (x)$
be any
$\varphi (x)$
be any
![]() $\mathcal {L}_A(\Box )$
-formula with no free variables except possibly
$\mathcal {L}_A(\Box )$
-formula with no free variables except possibly
![]() $x$
, such that
$x$
, such that
![]() $T \vdash \exists x \Box \varphi (x)$
. By the Fixed Point Lemma, let
$T \vdash \exists x \Box \varphi (x)$
. By the Fixed Point Lemma, let
![]() $\psi $
be a
$\psi $
be a
![]() $\Sigma (\mathrm {B})$
sentence satisfying
$\Sigma (\mathrm {B})$
sentence satisfying
Since
![]() $\mathbf {PA}_{\Box } \vdash \exists x \Box \varphi (x) \land \neg \mathrm {Pr}_T(\ulcorner \psi \urcorner ) \to \psi $
, we have
$\mathbf {PA}_{\Box } \vdash \exists x \Box \varphi (x) \land \neg \mathrm {Pr}_T(\ulcorner \psi \urcorner ) \to \psi $
, we have
![]() $T \vdash \mathrm {Pr}_T(\ulcorner \psi \urcorner ) \lor \psi $
. Since T is
$T \vdash \mathrm {Pr}_T(\ulcorner \psi \urcorner ) \lor \psi $
. Since T is
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {DC}$
by Corollary 5.32, we obtain
$\mathrm {DC}$
by Corollary 5.32, we obtain
![]() $T \vdash \psi $
. By the choice of
$T \vdash \psi $
. By the choice of
![]() $\psi $
,
$\psi $
,
Let p be a proof of
![]() $\psi $
in T, then
$\psi $
in T, then
![]() $T \vdash \mathrm {Prf}_T(\ulcorner \psi \urcorner , \overline {p})$
and thus
$T \vdash \mathrm {Prf}_T(\ulcorner \psi \urcorner , \overline {p})$
and thus
![]() $T \vdash \exists x \leq \overline {p} \, \Box \varphi (x)$
by (5). Then,
$T \vdash \exists x \leq \overline {p} \, \Box \varphi (x)$
by (5). Then,
![]() $T \vdash \Box \varphi (\overline {0}) \lor \cdots \lor \Box \varphi (\overline {p})$
. Since T has
$T \vdash \Box \varphi (\overline {0}) \lor \cdots \lor \Box \varphi (\overline {p})$
. Since T has
![]() $\mathrm {B}^{p+1}$
-
$\mathrm {B}^{p+1}$
-
![]() $\mathrm {DP}$
by Proposition 4.16.2, there exists
$\mathrm {DP}$
by Proposition 4.16.2, there exists
![]() $k \leq p$
such that
$k \leq p$
such that
![]() $T \vdash \Box \varphi (\overline {k})$
. Therefore, T has
$T \vdash \Box \varphi (\overline {k})$
. Therefore, T has
![]() $\mathrm {B}$
-
$\mathrm {B}$
-
![]() $\mathrm {EP}$
.
$\mathrm {EP}$
.
![]() $(2 \Rightarrow 3)$
: Let
$(2 \Rightarrow 3)$
: Let
![]() $\varphi (x)$
be any
$\varphi (x)$
be any
![]() $\Sigma (\mathrm {B})$
formula without having free variables except
$\Sigma (\mathrm {B})$
formula without having free variables except
![]() $x$
such that
$x$
such that
![]() $T \vdash \exists x \varphi (x)$
. By Proposition 3.10, there exists a
$T \vdash \exists x \varphi (x)$
. By Proposition 3.10, there exists a
![]() $\Delta (\mathrm {B})$
formula
$\Delta (\mathrm {B})$
formula
![]() $\psi (x, y)$
such that
$\psi (x, y)$
such that
![]() $\mathbf {PA}_{\Box } \vdash \varphi (x) \leftrightarrow \exists y \psi (x, y)$
. Also, by Lemma 5.36,
$\mathbf {PA}_{\Box } \vdash \varphi (x) \leftrightarrow \exists y \psi (x, y)$
. Also, by Lemma 5.36,
![]() $\mathbf {PA}_{\Box } \vdash \psi (x, y) \leftrightarrow \exists \vec {v} \psi ^*(x, y, \vec {v})$
. Then,
$\mathbf {PA}_{\Box } \vdash \psi (x, y) \leftrightarrow \exists \vec {v} \psi ^*(x, y, \vec {v})$
. Then,
![]() $T \vdash \exists x \exists y \exists \vec {v} \psi ^*(x, y, \vec {v})$
and
$T \vdash \exists x \exists y \exists \vec {v} \psi ^*(x, y, \vec {v})$
and
Here
![]() $\langle x, y, \vec {v} \rangle $
is an appropriate iteration of usual
$\langle x, y, \vec {v} \rangle $
is an appropriate iteration of usual
![]() $\Delta _0$
representable bijective pairing function
$\Delta _0$
representable bijective pairing function
![]() $\langle \cdot , \cdot \rangle $
. We may assume that
$\langle \cdot , \cdot \rangle $
. We may assume that
![]() $\mathbf {PA}$
proves
$\mathbf {PA}$
proves
![]() $x\, {\leq }\, \langle x, y \rangle $
and
$x\, {\leq }\, \langle x, y \rangle $
and
![]() $y \, {\leq } \, \langle x, y \rangle $
. By Lemma 5.34,
$y \, {\leq } \, \langle x, y \rangle $
. By Lemma 5.34,
By
![]() $\mathrm {B}$
-
$\mathrm {B}$
-
![]() $\mathrm {EP}$
, there exists a natural number
$\mathrm {EP}$
, there exists a natural number
![]() $k$
such that
$k$
such that
For the unique p, q, and
![]() $\vec {r}$
such that
$\vec {r}$
such that
![]() $k = \langle p, q, \vec {r} \rangle $
,
$k = \langle p, q, \vec {r} \rangle $
,
By Lemma 5.37, we obtain
![]() $T \vdash \psi (\overline {p}, \overline {q})$
. Then,
$T \vdash \psi (\overline {p}, \overline {q})$
. Then,
![]() $T \vdash \varphi (\overline {p})$
. Therefore, T has
$T \vdash \varphi (\overline {p})$
. Therefore, T has
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {EP}$
.
$\mathrm {EP}$
.
![]() $(3 \Rightarrow 4)$
: By Proposition 4.18.2.
$(3 \Rightarrow 4)$
: By Proposition 4.18.2.
![]() $(4 \Rightarrow 1)$
: This is trivial.
$(4 \Rightarrow 1)$
: This is trivial.
In order to derive the equivalence of
![]() $\mathrm {MDP}$
and
$\mathrm {MDP}$
and
![]() $\mathrm {MEP}$
from Theorem 5.38, we prove a proposition that connects
$\mathrm {MEP}$
from Theorem 5.38, we prove a proposition that connects
![]() $\mathrm {MDP}$
(resp.
$\mathrm {MDP}$
(resp.
![]() $\mathrm {MEP}$
) and
$\mathrm {MEP}$
) and
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {DP}$
(resp.
$\mathrm {DP}$
(resp.
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {EP}$
).
$\mathrm {EP}$
).
Proposition 5.39. Let T be any r.e. extension of
![]() $\mathbf {PA}(\mathbf {K4})$
.
$\mathbf {PA}(\mathbf {K4})$
.
-
1. If T has
 $\mathrm {MDP}$
, then T also has
$\mathrm {MDP}$
, then T also has
 $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
 $\mathrm {DP}$
.
$\mathrm {DP}$
. -
2. If T has
 $\mathrm {MEP}$
, then T also has
$\mathrm {MEP}$
, then T also has
 $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
 $\mathrm {EP}$
.
$\mathrm {EP}$
.
Proof. 1. Let
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
be any
$\psi $
be any
![]() $\Sigma (\mathrm {B})$
sentences such that
$\Sigma (\mathrm {B})$
sentences such that
![]() $T \vdash \varphi \lor \psi $
. By Theorem 3.13,
$T \vdash \varphi \lor \psi $
. By Theorem 3.13,
![]() $T \vdash \Box \varphi \lor \Box \psi $
. By
$T \vdash \Box \varphi \lor \Box \psi $
. By
![]() $\mathrm {MDP}$
, we obtain
$\mathrm {MDP}$
, we obtain
![]() $T \vdash \varphi $
or
$T \vdash \varphi $
or
![]() $T \vdash \psi $
. Therefore, T has
$T \vdash \psi $
. Therefore, T has
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {DP}$
.
$\mathrm {DP}$
.
Clause 2 is proved similarly.
Corollary 5.40. For any r.e. extension T of
![]() $\mathbf {PA}(\mathbf {K4})$
, T has
$\mathbf {PA}(\mathbf {K4})$
, T has
![]() $\mathrm {MDP}$
if and only if T has
$\mathrm {MDP}$
if and only if T has
![]() $\mathrm {MEP}$
.
$\mathrm {MEP}$
.
Proof. Since
![]() $\mathrm {MEP}$
implies
$\mathrm {MEP}$
implies
![]() $\mathrm {MDP}$
by Proposition 4.18.1, it suffices to show that
$\mathrm {MDP}$
by Proposition 4.18.1, it suffices to show that
![]() $\mathrm {MDP}$
implies
$\mathrm {MDP}$
implies
![]() $\mathrm {MEP}$
. We may assume that T is consistent. If T has
$\mathrm {MEP}$
. We may assume that T is consistent. If T has
![]() $\mathrm {MDP}$
, then T has
$\mathrm {MDP}$
, then T has
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {DP}$
by Proposition 5.39. Also, T is closed under the box elimination rule by Proposition 4.17. Then,
$\mathrm {DP}$
by Proposition 5.39. Also, T is closed under the box elimination rule by Proposition 4.17. Then,
![]() $T \nvdash \Box \bot $
by the consistency of T. By Theorem 5.38, T has
$T \nvdash \Box \bot $
by the consistency of T. By Theorem 5.38, T has
![]() $\mathrm {B}$
-
$\mathrm {B}$
-
![]() $\mathrm {EP}$
. By Proposition 4.17 again, we conclude that T has
$\mathrm {EP}$
. By Proposition 4.17 again, we conclude that T has
![]() $\mathrm {MEP}$
.
$\mathrm {MEP}$
.
Remark 5.41. In the introduction, we imprecisely mentioned the result of Friedman and Sheard [Reference Friedman and Sheard6]. Firstly, Friedman and Sheard actually proved their theorem in the setting where the use of the rule Nec and the axiom
![]() $\forall \vec {x}(\Box (\varphi \to \psi ) \to (\Box \varphi \to \Box \psi ))$
is restricted, that is, in the non-normal setting. In our normal setting, the following result follows from their theorem: For any r.e. extension T of
$\forall \vec {x}(\Box (\varphi \to \psi ) \to (\Box \varphi \to \Box \psi ))$
is restricted, that is, in the non-normal setting. In our normal setting, the following result follows from their theorem: For any r.e. extension T of
![]() $\mathbf {PA}(\mathbf {K4}) + \{\forall \vec {x} \Box (\Box \varphi \to \varphi ) \mid \varphi \in \Delta _0\}$
, if T is closed under the box elimination rule, then T has
$\mathbf {PA}(\mathbf {K4}) + \{\forall \vec {x} \Box (\Box \varphi \to \varphi ) \mid \varphi \in \Delta _0\}$
, if T is closed under the box elimination rule, then T has
![]() $\mathrm {B}$
-
$\mathrm {B}$
-
![]() $\mathrm {DP}$
if and only if T has
$\mathrm {DP}$
if and only if T has
![]() $\mathrm {B}$
-
$\mathrm {B}$
-
![]() $\mathrm {EP}$
. Then, in the light of Proposition 4.17, this statement can be rewritten as follows: For any r.e. extension T of
$\mathrm {EP}$
. Then, in the light of Proposition 4.17, this statement can be rewritten as follows: For any r.e. extension T of
![]() $\mathbf {PA}(\mathbf {K4}) + \{\forall \vec {x} \Box (\Box \varphi \to \varphi ) \mid \varphi \in \Delta _0\}$
, T has
$\mathbf {PA}(\mathbf {K4}) + \{\forall \vec {x} \Box (\Box \varphi \to \varphi ) \mid \varphi \in \Delta _0\}$
, T has
![]() $\mathrm {MDP}$
if and only if T has
$\mathrm {MDP}$
if and only if T has
![]() $\mathrm {MEP}$
. Therefore, our Corollary 5.40 shows that the same consequence is obtained without using the axiom scheme
$\mathrm {MEP}$
. Therefore, our Corollary 5.40 shows that the same consequence is obtained without using the axiom scheme
![]() $\{\forall \vec {x} \Box (\Box \varphi \to \varphi ) \mid \varphi \in \Delta _0\}$
. Notice that by Theorem 2.8, over
$\{\forall \vec {x} \Box (\Box \varphi \to \varphi ) \mid \varphi \in \Delta _0\}$
. Notice that by Theorem 2.8, over
![]() $\mathbf {PA}(\mathbf {K})$
,
$\mathbf {PA}(\mathbf {K})$
,
![]() $\{\forall \vec {x} \Box (\Box \varphi \to \varphi ) \mid \varphi \in \Delta _0\}$
is equivalent to a single sentence
$\{\forall \vec {x} \Box (\Box \varphi \to \varphi ) \mid \varphi \in \Delta _0\}$
is equivalent to a single sentence
![]() $\Box \neg \Box \bot $
.
$\Box \neg \Box \bot $
.
6 Generalizations of the notions of soundness and
 $\Sigma _1$
-soundness
$\Sigma _1$
-soundness
In this section, we introduce several notions related to the soundness of theories of modal arithmetic with respect to
![]() $\mathcal {L}_A(\Box )$
-sentences. This section consists of three subsections. In the first subsection, we introduce the notion of the
$\mathcal {L}_A(\Box )$
-sentences. This section consists of three subsections. In the first subsection, we introduce the notion of the
![]() $\mathcal {L}_A(\Box )$
-soundness and prove that several
$\mathcal {L}_A(\Box )$
-soundness and prove that several
![]() $\mathcal {L}_A(\Box )$
-theories are actually
$\mathcal {L}_A(\Box )$
-theories are actually
![]() $\mathcal {L}_A(\Box )$
-sound. In the second subsection, we introduce the notions of the
$\mathcal {L}_A(\Box )$
-sound. In the second subsection, we introduce the notions of the
![]() $\Sigma (\mathrm {B})$
-soundness and the weak
$\Sigma (\mathrm {B})$
-soundness and the weak
![]() $\Sigma (\mathrm {B})$
-soundness. Then, we prove that over appropriate theories, the
$\Sigma (\mathrm {B})$
-soundness. Then, we prove that over appropriate theories, the
![]() $\Sigma (\mathrm {B})$
-soundness and the weak
$\Sigma (\mathrm {B})$
-soundness and the weak
![]() $\Sigma (\mathrm {B})$
-soundness characterize
$\Sigma (\mathrm {B})$
-soundness characterize
![]() $\mathrm {MDP}$
and
$\mathrm {MDP}$
and
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {DP}$
, respectively. In the last subsection, we prove two non-implications between the properties as applications of the results we have obtained so far.
$\mathrm {DP}$
, respectively. In the last subsection, we prove two non-implications between the properties as applications of the results we have obtained so far.
6.1
 $\mathcal {L}_A(\Box )$
-soundness
$\mathcal {L}_A(\Box )$
-soundness
We formulate the notion of the
![]() $\mathcal {L}_A(\Box )$
-soundness under the interpretation that boxed formulas represent the provability of some formula in the standard model
$\mathcal {L}_A(\Box )$
-soundness under the interpretation that boxed formulas represent the provability of some formula in the standard model
![]() $\mathbb {N}$
of arithmetic. To do so, we once translate each
$\mathbb {N}$
of arithmetic. To do so, we once translate each
![]() $\mathcal {L}_A(\Box )$
-sentence into an
$\mathcal {L}_A(\Box )$
-sentence into an
![]() $\mathcal {L}_A$
-sentence using a provability predicate, and then consider the truth of the translated sentence in
$\mathcal {L}_A$
-sentence using a provability predicate, and then consider the truth of the translated sentence in
![]() $\mathbb {N}$
. First, we introduce two types of translations
$\mathbb {N}$
. First, we introduce two types of translations
![]() $\pi _T$
and
$\pi _T$
and
![]() $\pi ^{\prime }_T$
.
$\pi ^{\prime }_T$
.
Definition 6.42 (
 $\pi $
-translations)
$\pi $
-translations)
Let T be any r.e.
![]() $\mathcal {L}_A(\Box )$
-theory. We define a translation
$\mathcal {L}_A(\Box )$
-theory. We define a translation
![]() $\pi _T$
of
$\pi _T$
of
![]() $\mathcal {L}_A(\Box )$
-formulas into
$\mathcal {L}_A(\Box )$
-formulas into
![]() $\mathcal {L}_A$
-formulas inductively as follows:
$\mathcal {L}_A$
-formulas inductively as follows:
-
1. If
 $\varphi $
is an
$\varphi $
is an
 $\mathcal {L}_A$
-formula, then
$\mathcal {L}_A$
-formula, then
 $\pi _T(\varphi ) : \equiv \varphi $
.
$\pi _T(\varphi ) : \equiv \varphi $
. -
2.
 $\pi _T$
preserves logical connectives and quantifiers.
$\pi _T$
preserves logical connectives and quantifiers. -
3.
 $\pi _T(\Box \varphi (\vec {x})) : \equiv \mathrm {Pr}_T(\ulcorner \varphi (\vec {\dot {x}}) \urcorner )$
.
$\pi _T(\Box \varphi (\vec {x})) : \equiv \mathrm {Pr}_T(\ulcorner \varphi (\vec {\dot {x}}) \urcorner )$
.
Here
![]() $\ulcorner \varphi (\vec {\dot {x}})\urcorner $
is a primitive recursive term corresponding to a primitive recursive function calculating the Gödel number of
$\ulcorner \varphi (\vec {\dot {x}})\urcorner $
is a primitive recursive term corresponding to a primitive recursive function calculating the Gödel number of
![]() $\varphi (\vec {\overline {n}})$
from
$\varphi (\vec {\overline {n}})$
from
![]() $\vec {n}$
. Note that
$\vec {n}$
. Note that
![]() $\vec {x}$
are free variables in the formula
$\vec {x}$
are free variables in the formula
![]() $\mathrm {Pr}_T(\ulcorner \varphi (\vec {\dot {x}})\urcorner )$
.
$\mathrm {Pr}_T(\ulcorner \varphi (\vec {\dot {x}})\urcorner )$
.
Definition 6.43 (
 $\pi '$
-translations)
$\pi '$
-translations)
Let T be any r.e.
![]() $\mathcal {L}_A(\Box )$
-theory. We define a translation
$\mathcal {L}_A(\Box )$
-theory. We define a translation
![]() $\pi ^{\prime }_T$
of
$\pi ^{\prime }_T$
of
![]() $\mathcal {L}_A(\Box )$
-formulas into
$\mathcal {L}_A(\Box )$
-formulas into
![]() $\mathcal {L}_A$
-formulas inductively as follows:
$\mathcal {L}_A$
-formulas inductively as follows:
-
1. If
 $\varphi $
is an
$\varphi $
is an
 $\mathcal {L}_A$
-formula, then
$\mathcal {L}_A$
-formula, then
 $\pi ^{\prime }_T(\varphi ) : \equiv \varphi $
.
$\pi ^{\prime }_T(\varphi ) : \equiv \varphi $
. -
2.
 $\pi ^{\prime }_T$
preserves logical connectives and quantifiers.
$\pi ^{\prime }_T$
preserves logical connectives and quantifiers. -
3.
 $\pi ^{\prime }_T(\Box \varphi (\vec {x})) : \equiv \mathrm {Pr}_T(\ulcorner \varphi (\vec {\dot {x}}) \urcorner ) \land \pi ^{\prime }_T(\varphi (\vec {x}))$
.
$\pi ^{\prime }_T(\Box \varphi (\vec {x})) : \equiv \mathrm {Pr}_T(\ulcorner \varphi (\vec {\dot {x}}) \urcorner ) \land \pi ^{\prime }_T(\varphi (\vec {x}))$
.
The translation
![]() $\pi ^{\prime }_T$
is a formalization of Shapiro’s slash interpretation [Reference Shapiro21], introduced in [Reference Halbach and Horsten11] under the name
$\pi ^{\prime }_T$
is a formalization of Shapiro’s slash interpretation [Reference Shapiro21], introduced in [Reference Halbach and Horsten11] under the name
![]() $\sigma _T$
.
$\sigma _T$
.
Definition 6.44. Let T be any r.e.
![]() $\mathcal {L}_A(\Box )$
-theory.
$\mathcal {L}_A(\Box )$
-theory.
-
• T is said to be
 $\mathcal {L}_A(\Box )$
-sound if for any
$\mathcal {L}_A(\Box )$
-sound if for any
 $\mathcal {L}_A(\Box )$
-sentence
$\mathcal {L}_A(\Box )$
-sentence
 $\varphi $
, if
$\varphi $
, if
 $T \vdash \varphi $
, then
$T \vdash \varphi $
, then
 $\mathbb {N} \models \pi _T(\varphi )$
.
$\mathbb {N} \models \pi _T(\varphi )$
. -
• T is said to be alternatively
 $\mathcal {L}_A(\Box )$
-sound if for any
$\mathcal {L}_A(\Box )$
-sound if for any
 $\mathcal {L}_A(\Box )$
-sentence
$\mathcal {L}_A(\Box )$
-sentence
 $\varphi $
, if
$\varphi $
, if
 $T \vdash \varphi $
, then
$T \vdash \varphi $
, then
 $\mathbb {N} \models \pi ^{\prime }_T(\varphi )$
.
$\mathbb {N} \models \pi ^{\prime }_T(\varphi )$
.
Actually, these two notions are equivalent.
Proposition 6.45. For any r.e.
![]() $\mathcal {L}_A(\Box )$
-theory T, the following are equivalent:
$\mathcal {L}_A(\Box )$
-theory T, the following are equivalent:
-
1. T is
 $\mathcal {L}_A(\Box )$
-sound.
$\mathcal {L}_A(\Box )$
-sound. -
2. T is alternatively
 $\mathcal {L}_A(\Box )$
-sound.
$\mathcal {L}_A(\Box )$
-sound.
Proof.
![]() $(1 \Rightarrow 2)$
: Suppose that T is
$(1 \Rightarrow 2)$
: Suppose that T is
![]() $\mathcal {L}_A(\Box )$
-sound. We prove by induction on the construction of
$\mathcal {L}_A(\Box )$
-sound. We prove by induction on the construction of
![]() $\varphi $
that for all
$\varphi $
that for all
![]() $\mathcal {L}_A(\Box )$
-sentences
$\mathcal {L}_A(\Box )$
-sentences
![]() $\varphi $
,
$\varphi $
,
![]() $\mathbb {N} \models \pi _T(\varphi ) \leftrightarrow \pi _T'(\varphi )$
. If
$\mathbb {N} \models \pi _T(\varphi ) \leftrightarrow \pi _T'(\varphi )$
. If
![]() $\varphi $
is an atomic
$\varphi $
is an atomic
![]() $\mathcal {L}_A$
-sentence, then
$\mathcal {L}_A$
-sentence, then
![]() $\pi _T(\varphi )$
coincides with
$\pi _T(\varphi )$
coincides with
![]() $\pi ^{\prime }_T(\varphi )$
. The cases for Boolean connectives are easy.
$\pi ^{\prime }_T(\varphi )$
. The cases for Boolean connectives are easy.
If
![]() $\varphi $
is of the form
$\varphi $
is of the form
![]() $\forall x \psi (x)$
, then for any natural number
$\forall x \psi (x)$
, then for any natural number
![]() $n$
,
$n$
,
![]() $\mathbb {N} \models \pi _T(\psi (\overline {n})) \leftrightarrow \pi ^{\prime }_T(\psi (\overline {n}))$
by the induction hypothesis. Then,
$\mathbb {N} \models \pi _T(\psi (\overline {n})) \leftrightarrow \pi ^{\prime }_T(\psi (\overline {n}))$
by the induction hypothesis. Then,
![]() $\mathbb {N} \models \forall x \bigl (\pi _T(\psi (x)) \leftrightarrow \pi ^{\prime }_T(\psi (x) \bigr )$
and hence
$\mathbb {N} \models \forall x \bigl (\pi _T(\psi (x)) \leftrightarrow \pi ^{\prime }_T(\psi (x) \bigr )$
and hence
![]() $\mathbb {N} \models \forall x \pi _T(\psi (x)) \leftrightarrow \forall x \pi ^{\prime }_T(\psi (x))$
. This means
$\mathbb {N} \models \forall x \pi _T(\psi (x)) \leftrightarrow \forall x \pi ^{\prime }_T(\psi (x))$
. This means
![]() $\mathbb {N} \models \pi _T(\varphi ) \leftrightarrow \pi ^{\prime }_T(\varphi )$
.
$\mathbb {N} \models \pi _T(\varphi ) \leftrightarrow \pi ^{\prime }_T(\varphi )$
.
Suppose that
![]() $\varphi $
is of the form
$\varphi $
is of the form
![]() $\Box \psi $
. Since
$\Box \psi $
. Since
![]() $\pi _T(\Box \psi )$
is
$\pi _T(\Box \psi )$
is
![]() $\mathrm {Pr}_T(\ulcorner \psi \urcorner )$
, by the
$\mathrm {Pr}_T(\ulcorner \psi \urcorner )$
, by the
![]() $\mathcal {L}_A(\Box )$
-soundness of T,
$\mathcal {L}_A(\Box )$
-soundness of T,
![]() $\mathbb {N} \models \pi _T(\Box \psi )$
if and only if
$\mathbb {N} \models \pi _T(\Box \psi )$
if and only if
![]() $\mathbb {N} \models \mathrm {Pr}_T(\ulcorner \psi \urcorner ) \land \pi _T(\psi )$
. By the induction hypothesis,
$\mathbb {N} \models \mathrm {Pr}_T(\ulcorner \psi \urcorner ) \land \pi _T(\psi )$
. By the induction hypothesis,
![]() $\mathbb {N} \models \mathrm {Pr}_T(\ulcorner \psi \urcorner ) \land \pi _T(\psi )$
if and only if
$\mathbb {N} \models \mathrm {Pr}_T(\ulcorner \psi \urcorner ) \land \pi _T(\psi )$
if and only if
![]() $\mathbb {N} \models \mathrm {Pr}_T(\ulcorner \psi \urcorner ) \land \pi ^{\prime }_T(\psi )$
. Thus,
$\mathbb {N} \models \mathrm {Pr}_T(\ulcorner \psi \urcorner ) \land \pi ^{\prime }_T(\psi )$
. Thus,
![]() $\mathbb {N} \models \pi _T(\Box \psi ) \leftrightarrow \pi ^{\prime }_T(\Box \psi )$
.
$\mathbb {N} \models \pi _T(\Box \psi ) \leftrightarrow \pi ^{\prime }_T(\Box \psi )$
.
![]() $(2 \Rightarrow 1)$
: Suppose that T is alternatively
$(2 \Rightarrow 1)$
: Suppose that T is alternatively
![]() $\mathcal {L}_A(\Box )$
-sound. Similarly, we only prove that for all
$\mathcal {L}_A(\Box )$
-sound. Similarly, we only prove that for all
![]() $\mathcal {L}_A(\Box )$
-sentences
$\mathcal {L}_A(\Box )$
-sentences
![]() $\psi $
,
$\psi $
,
![]() $\mathbb {N} \models \pi ^{\prime }_T(\Box \psi ) \leftrightarrow \pi _T(\Box \psi )$
.
$\mathbb {N} \models \pi ^{\prime }_T(\Box \psi ) \leftrightarrow \pi _T(\Box \psi )$
.
![]() $\mathbb {N} \models \pi ^{\prime }_T(\Box \psi )$
is equivalent to
$\mathbb {N} \models \pi ^{\prime }_T(\Box \psi )$
is equivalent to
![]() $\mathbb {N} \models \mathrm {Pr}_T(\ulcorner \psi \urcorner ) \land \pi ^{\prime }_T(\psi )$
. Then, by the alternative
$\mathbb {N} \models \mathrm {Pr}_T(\ulcorner \psi \urcorner ) \land \pi ^{\prime }_T(\psi )$
. Then, by the alternative
![]() $\mathcal {L}_A(\Box )$
-soundness of T, this is equivalent to
$\mathcal {L}_A(\Box )$
-soundness of T, this is equivalent to
![]() $\mathbb {N} \models \mathrm {Pr}_T(\ulcorner \psi \urcorner )$
. This is exactly
$\mathbb {N} \models \mathrm {Pr}_T(\ulcorner \psi \urcorner )$
. This is exactly
![]() $\mathbb {N} \models \pi _T(\Box \psi )$
.
$\mathbb {N} \models \pi _T(\Box \psi )$
.
Here we show some propositions that help to prove the
![]() $\mathcal {L}_A(\Box )$
-soundness of each
$\mathcal {L}_A(\Box )$
-soundness of each
![]() $\mathcal {L}_A(\Box )$
-theory.
$\mathcal {L}_A(\Box )$
-theory.
Proposition 6.46. Let T be an
![]() $\mathcal {L}_A(\Box )$
-theory obtained by adding some axioms of
$\mathcal {L}_A(\Box )$
-theory obtained by adding some axioms of
![]() $\mathbf {PA}(\mathbf {GL})$
into
$\mathbf {PA}(\mathbf {GL})$
into
![]() $\mathbf {PA}_{\Box }$
. For any
$\mathbf {PA}_{\Box }$
. For any
![]() $\mathcal {L}_A(\Box )$
-formula
$\mathcal {L}_A(\Box )$
-formula
![]() $\varphi $
, if
$\varphi $
, if
![]() $T \vdash \varphi $
, then for any r.e. extension U of T,
$T \vdash \varphi $
, then for any r.e. extension U of T,
![]() $\mathbf {PA} \vdash \pi _U(\varphi )$
.
$\mathbf {PA} \vdash \pi _U(\varphi )$
.
Proof. Let U be any r.e. extension of T. As in the proof of Proposition 2.3, by induction on the length of proofs of
![]() $\varphi $
in T, we prove that for any
$\varphi $
in T, we prove that for any
![]() $\mathcal {L}_A(\Box )$
-formula
$\mathcal {L}_A(\Box )$
-formula
![]() $\varphi $
, if
$\varphi $
, if
![]() $T \vdash \varphi $
, then
$T \vdash \varphi $
, then
![]() $\mathbf {PA} \vdash \pi _U(\varphi )$
. We only give proofs of the following four cases.
$\mathbf {PA} \vdash \pi _U(\varphi )$
. We only give proofs of the following four cases.
-
• If
 $\varphi $
is
$\varphi $
is
 $\forall \vec {x} \bigl (\Box (\psi (\vec {x}) \to \sigma (\vec {x})) \to (\Box \psi (\vec {x}) \to \Box \sigma (\vec {x})) \bigr )$
, then
$\forall \vec {x} \bigl (\Box (\psi (\vec {x}) \to \sigma (\vec {x})) \to (\Box \psi (\vec {x}) \to \Box \sigma (\vec {x})) \bigr )$
, then
 $\pi _U(\varphi )$
is and this is provable in
$\pi _U(\varphi )$
is and this is provable in $$\begin{align*}\forall \vec{x} \bigl(\mathrm{Pr}_U(\ulcorner\psi(\vec{\dot{x}}) \to \sigma(\vec{\dot{x}})\urcorner) \to (\mathrm{Pr}_U(\ulcorner\psi(\vec{\dot{x}})\urcorner) \to \mathrm{Pr}_U(\ulcorner\sigma(\vec{\dot{x}})\urcorner)) \bigr), \end{align*}$$
$$\begin{align*}\forall \vec{x} \bigl(\mathrm{Pr}_U(\ulcorner\psi(\vec{\dot{x}}) \to \sigma(\vec{\dot{x}})\urcorner) \to (\mathrm{Pr}_U(\ulcorner\psi(\vec{\dot{x}})\urcorner) \to \mathrm{Pr}_U(\ulcorner\sigma(\vec{\dot{x}})\urcorner)) \bigr), \end{align*}$$
 $\mathbf {PA}$
.
$\mathbf {PA}$
.
-
• If
 $\varphi $
is
$\varphi $
is
 $\forall \vec {x} \bigl (\Box \psi (\vec {x}) \to \Box \Box \psi (\vec {x}) \bigr )$
, then
$\forall \vec {x} \bigl (\Box \psi (\vec {x}) \to \Box \Box \psi (\vec {x}) \bigr )$
, then
 $\pi _U(\varphi )$
is Since
$\pi _U(\varphi )$
is Since $$\begin{align*}\forall \vec{x} \bigl(\mathrm{Pr}_U(\ulcorner\psi(\vec{\dot{x}})\urcorner) \to \mathrm{Pr}_U(\ulcorner\Box \psi(\vec{\dot{x}})\urcorner) \bigr). \end{align*}$$
$$\begin{align*}\forall \vec{x} \bigl(\mathrm{Pr}_U(\ulcorner\psi(\vec{\dot{x}})\urcorner) \to \mathrm{Pr}_U(\ulcorner\Box \psi(\vec{\dot{x}})\urcorner) \bigr). \end{align*}$$
 $\mathbf {PA}$
proves the fact that the consequences of U are closed under the rule Nec, this sentence is provable in
$\mathbf {PA}$
proves the fact that the consequences of U are closed under the rule Nec, this sentence is provable in
 $\mathbf {PA}$
.
$\mathbf {PA}$
.
-
• If
 $\varphi $
is
$\varphi $
is
 $\forall \vec {x} \bigl (\Box (\Box \psi (\vec {x}) \to \psi (\vec {x})) \to \Box \psi (\vec {x}) \bigr )$
, then we reason as follows: By invoking Nec, Since U is an extension of T, we have
$\forall \vec {x} \bigl (\Box (\Box \psi (\vec {x}) \to \psi (\vec {x})) \to \Box \psi (\vec {x}) \bigr )$
, then we reason as follows: By invoking Nec, Since U is an extension of T, we have $$\begin{align*}\mathbf{PA} \vdash \mathrm{Pr}_U(\ulcorner\Box \psi(\vec{\dot{x}}) \to \psi(\vec{\dot{x}})\urcorner) \to \mathrm{Pr}_U(\ulcorner\Box(\Box \psi(\vec{\dot{x}}) \to \psi(\vec{\dot{x}}))\urcorner). \end{align*}$$
$$\begin{align*}\mathbf{PA} \vdash \mathrm{Pr}_U(\ulcorner\Box \psi(\vec{\dot{x}}) \to \psi(\vec{\dot{x}})\urcorner) \to \mathrm{Pr}_U(\ulcorner\Box(\Box \psi(\vec{\dot{x}}) \to \psi(\vec{\dot{x}}))\urcorner). \end{align*}$$
 $\mathbf {PA} \vdash \mathrm {Pr}_U(\ulcorner \varphi \urcorner )$
and hence Then,
$\mathbf {PA} \vdash \mathrm {Pr}_U(\ulcorner \varphi \urcorner )$
and hence Then, $$\begin{align*}\mathbf{PA} \vdash \mathrm{Pr}_U(\ulcorner\Box(\Box \psi(\vec{\dot{x}}) \to \psi(\vec{\dot{x}}))\urcorner) \to \mathrm{Pr}_U(\ulcorner\Box \psi(\vec{\dot{x}})\urcorner). \end{align*}$$
and thus
$$\begin{align*}\mathbf{PA} \vdash \mathrm{Pr}_U(\ulcorner\Box(\Box \psi(\vec{\dot{x}}) \to \psi(\vec{\dot{x}}))\urcorner) \to \mathrm{Pr}_U(\ulcorner\Box \psi(\vec{\dot{x}})\urcorner). \end{align*}$$
and thus $$\begin{align*}\mathbf{PA} \vdash \mathrm{Pr}_U(\ulcorner\Box \psi(\vec{\dot{x}}) \to \psi(\vec{\dot{x}})\urcorner) \to \mathrm{Pr}_U(\ulcorner\Box \psi(\vec{\dot{x}})\urcorner), \end{align*}$$
This means
$$\begin{align*}\mathbf{PA} \vdash \mathrm{Pr}_U(\ulcorner\Box \psi(\vec{\dot{x}}) \to \psi(\vec{\dot{x}})\urcorner) \to \mathrm{Pr}_U(\ulcorner\Box \psi(\vec{\dot{x}})\urcorner), \end{align*}$$
This means $$\begin{align*}\mathbf{PA} \vdash \mathrm{Pr}_U(\ulcorner\Box \psi(\vec{\dot{x}}) \to \psi(\vec{\dot{x}})\urcorner) \to \mathrm{Pr}_U(\ulcorner\psi(\vec{\dot{x}})\urcorner). \end{align*}$$
$$\begin{align*}\mathbf{PA} \vdash \mathrm{Pr}_U(\ulcorner\Box \psi(\vec{\dot{x}}) \to \psi(\vec{\dot{x}})\urcorner) \to \mathrm{Pr}_U(\ulcorner\psi(\vec{\dot{x}})\urcorner). \end{align*}$$
 $\mathbf {PA} \vdash \pi _U(\varphi )$
.
$\mathbf {PA} \vdash \pi _U(\varphi )$
.
-
• If
 $\varphi (\vec {x})$
is derived from
$\varphi (\vec {x})$
is derived from
 $\psi (\vec {x})$
by Nec, then
$\psi (\vec {x})$
by Nec, then
 $\varphi (\vec {x}) \equiv \Box \psi (\vec {x})$
. Since
$\varphi (\vec {x}) \equiv \Box \psi (\vec {x})$
. Since
 $U \vdash \psi (\vec {x})$
,
$U \vdash \psi (\vec {x})$
,
 $\mathbf {PA} \vdash \mathrm {Pr}_U(\ulcorner \psi (\vec {\dot {x}})\urcorner )$
. Thus,
$\mathbf {PA} \vdash \mathrm {Pr}_U(\ulcorner \psi (\vec {\dot {x}})\urcorner )$
. Thus,
 $\mathbf {PA} \vdash \pi _U(\varphi (\vec {x}))$
.
$\mathbf {PA} \vdash \pi _U(\varphi (\vec {x}))$
.
Proposition 6.47. Let T be an
![]() $\mathcal {L}_A(\Box )$
-theory obtained by adding some axioms of
$\mathcal {L}_A(\Box )$
-theory obtained by adding some axioms of
![]() $\mathbf {PA}(\mathbf {GL})$
into
$\mathbf {PA}(\mathbf {GL})$
into
![]() $\mathbf {PA}_{\Box }$
, and let U be any r.e. extension of T. If
$\mathbf {PA}_{\Box }$
, and let U be any r.e. extension of T. If
![]() $\mathbb {N} \models \pi _U(\varphi )$
for all
$\mathbb {N} \models \pi _U(\varphi )$
for all
![]() $\varphi \in U \setminus T$
, then U is
$\varphi \in U \setminus T$
, then U is
![]() $\mathcal {L}_A(\Box )$
-sound.
$\mathcal {L}_A(\Box )$
-sound.
Proof. Suppose that
![]() $\mathbb {N} \models \pi _U(\varphi )$
for all
$\mathbb {N} \models \pi _U(\varphi )$
for all
![]() $\varphi \in U \setminus T$
. We prove by induction on the length of a proof of
$\varphi \in U \setminus T$
. We prove by induction on the length of a proof of
![]() $\varphi $
in U that for all
$\varphi $
in U that for all
![]() $\mathcal {L}_A$
-formulas
$\mathcal {L}_A$
-formulas
![]() $\varphi $
, if
$\varphi $
, if
![]() $U \vdash \varphi $
, then
$U \vdash \varphi $
, then
![]() $\mathbb {N} \models \pi _U(\forall \vec {x} \varphi )$
.
$\mathbb {N} \models \pi _U(\forall \vec {x} \varphi )$
.
-
• If
 $\varphi $
is an axiom of T or a logical axiom, then
$\varphi $
is an axiom of T or a logical axiom, then
 $\mathbf {PA} \vdash \pi _U(\forall \vec {x} \varphi )$
by Proposition 6.46. Thus,
$\mathbf {PA} \vdash \pi _U(\forall \vec {x} \varphi )$
by Proposition 6.46. Thus,
 $\mathbb {N} \models \pi _U(\forall \vec {x} \varphi )$
.
$\mathbb {N} \models \pi _U(\forall \vec {x} \varphi )$
. -
• If
 $\varphi $
is in
$\varphi $
is in
 $U \setminus T$
, then
$U \setminus T$
, then
 $\mathbb {N} \models \pi _U(\varphi )$
by the supposition.
$\mathbb {N} \models \pi _U(\varphi )$
by the supposition. -
• If
 $\varphi $
is derived from
$\varphi $
is derived from
 $\psi $
and
$\psi $
and
 $\psi \to \varphi $
by MP, then by the induction hypothesis,
$\psi \to \varphi $
by MP, then by the induction hypothesis,
 $\mathbb {N} \models \pi _U(\forall \vec {x} \psi )$
and
$\mathbb {N} \models \pi _U(\forall \vec {x} \psi )$
and
 $\mathbb {N} \models \pi _U(\forall \vec {x}( \psi \to \varphi ))$
. Then,
$\mathbb {N} \models \pi _U(\forall \vec {x}( \psi \to \varphi ))$
. Then,
 $\mathbb {N} \models \pi _U(\forall \vec {x} \varphi )$
.
$\mathbb {N} \models \pi _U(\forall \vec {x} \varphi )$
. -
• If
 $\varphi $
is derived from
$\varphi $
is derived from
 $\psi (y)$
by Gen, then
$\psi (y)$
by Gen, then
 $\varphi \equiv \forall y \psi (y)$
. By the induction hypothesis,
$\varphi \equiv \forall y \psi (y)$
. By the induction hypothesis,
 $\mathbb {N} \models \pi _U(\forall \vec {x} \forall y \psi (y))$
. Hence,
$\mathbb {N} \models \pi _U(\forall \vec {x} \forall y \psi (y))$
. Hence,
 $\mathbb {N} \models \pi _U(\forall \vec {x} \varphi )$
.
$\mathbb {N} \models \pi _U(\forall \vec {x} \varphi )$
. -
• If
 $\varphi $
is derived from
$\varphi $
is derived from
 $\psi $
by Nec, then
$\psi $
by Nec, then
 $\varphi \equiv \Box \psi $
and
$\varphi \equiv \Box \psi $
and
 $U \vdash \psi $
. We have
$U \vdash \psi $
. We have
 $\mathbb {N} \models \forall \vec {x} \, \mathrm {Pr}_U(\ulcorner \psi \urcorner )$
, and equivalently
$\mathbb {N} \models \forall \vec {x} \, \mathrm {Pr}_U(\ulcorner \psi \urcorner )$
, and equivalently
 $\mathbb {N} \models \pi _U(\forall \vec {x} \varphi )$
.
$\mathbb {N} \models \pi _U(\forall \vec {x} \varphi )$
.
Corollary 6.48. The theories
![]() $\mathbf {PA}_{\Box }$
,
$\mathbf {PA}_{\Box }$
,
![]() $\mathbf {PA}(\mathbf {K})$
,
$\mathbf {PA}(\mathbf {K})$
,
![]() $\mathbf {PA}(\mathbf {K4})$
, and
$\mathbf {PA}(\mathbf {K4})$
, and
![]() $\mathbf {PA}(\mathbf {GL})$
are
$\mathbf {PA}(\mathbf {GL})$
are
![]() $\mathcal {L}_A(\Box )$
-sound.
$\mathcal {L}_A(\Box )$
-sound.
Here, we give some more examples of
![]() $\mathcal {L}_A(\Box )$
-sound theories. Let
$\mathcal {L}_A(\Box )$
-sound theories. Let
![]() $x \in W_y$
be a
$x \in W_y$
be a
![]() $\Sigma _1$
formula saying that
$\Sigma _1$
formula saying that
![]() $x$
is in the y-th r.e. set. Reinhardt’s Weak Mechanistic Thesis (WMT) is the following schema:
$x$
is in the y-th r.e. set. Reinhardt’s Weak Mechanistic Thesis (WMT) is the following schema:
-
•
 $\exists y \forall x \bigl (\Box \varphi (x) \leftrightarrow x \in W_y \bigr )$
, where
$\exists y \forall x \bigl (\Box \varphi (x) \leftrightarrow x \in W_y \bigr )$
, where
 $\varphi (x)$
is an
$\varphi (x)$
is an
 $\mathcal {L}_A(\Box )$
-formula having lone free variable
$\mathcal {L}_A(\Box )$
-formula having lone free variable
 $x$
.
$x$
.
When
![]() $\Box $
is interpreted as knowledge, WMT can be thought as a formalization of “Knowledge is mechanical.” Concerning WMT, we obtain the following corollary to Proposition 6.47.
$\Box $
is interpreted as knowledge, WMT can be thought as a formalization of “Knowledge is mechanical.” Concerning WMT, we obtain the following corollary to Proposition 6.47.
Corollary 6.49. Let T be an r.e.
![]() $\mathcal {L}_A(\Box )$
-theory obtained by adding some axioms of
$\mathcal {L}_A(\Box )$
-theory obtained by adding some axioms of
![]() $\mathbf {PA}(\mathbf {GL})$
into
$\mathbf {PA}(\mathbf {GL})$
into
![]() $\mathbf {PA}_{\Box }$
. Then, the theory
$\mathbf {PA}_{\Box }$
. Then, the theory
![]() $U : = T + \mathrm {WMT}$
is
$U : = T + \mathrm {WMT}$
is
![]() $\mathcal {L}_A(\Box )$
-sound.
$\mathcal {L}_A(\Box )$
-sound.
Proof. Since
![]() $\mathrm {Pr}_U(\ulcorner \varphi (\dot {x})\urcorner )$
is a
$\mathrm {Pr}_U(\ulcorner \varphi (\dot {x})\urcorner )$
is a
![]() $\Sigma _1$
formula, there exists a natural number e such that
$\Sigma _1$
formula, there exists a natural number e such that
Then, we have
![]() $\mathbb {N} \models \pi _U \Bigl (\exists y \forall x \bigl (\Box \varphi (x) \leftrightarrow x \in W_y \bigr ) \Bigr )$
. By Proposition 6.47, the theory U is
$\mathbb {N} \models \pi _U \Bigl (\exists y \forall x \bigl (\Box \varphi (x) \leftrightarrow x \in W_y \bigr ) \Bigr )$
. By Proposition 6.47, the theory U is
![]() $\mathcal {L}_A(\Box )$
-sound.
$\mathcal {L}_A(\Box )$
-sound.
We prove an analogue of Proposition 6.46 with respect to
![]() $\pi '$
-translations.
$\pi '$
-translations.
Proposition 6.50. Let T be an
![]() $\mathcal {L}_A(\Box )$
-theory obtained by adding some axioms of
$\mathcal {L}_A(\Box )$
-theory obtained by adding some axioms of
![]() $\mathbf {PA}(\mathbf {S4})$
into
$\mathbf {PA}(\mathbf {S4})$
into
![]() $\mathbf {PA}_{\Box }$
. For any
$\mathbf {PA}_{\Box }$
. For any
![]() $\mathcal {L}_A(\Box )$
-formula
$\mathcal {L}_A(\Box )$
-formula
![]() $\varphi $
, if
$\varphi $
, if
![]() $T \vdash \varphi $
, then for any r.e. extension U of T,
$T \vdash \varphi $
, then for any r.e. extension U of T,
![]() $\mathbf {PA} \vdash \pi ^{\prime }_U(\varphi )$
.
$\mathbf {PA} \vdash \pi ^{\prime }_U(\varphi )$
.
Proof. Let U be any r.e. extension of T. As in the proof of Proposition 2.3, we prove by induction on the length of proofs of
![]() $\varphi $
in T that for any
$\varphi $
in T that for any
![]() $\mathcal {L}_A(\Box )$
-formula
$\mathcal {L}_A(\Box )$
-formula
![]() $\varphi $
, if
$\varphi $
, if
![]() $T \vdash \varphi $
, then
$T \vdash \varphi $
, then
![]() $\mathbf {PA} \vdash \pi ^{\prime }_U(\varphi )$
. We only give proofs of the following four cases.
$\mathbf {PA} \vdash \pi ^{\prime }_U(\varphi )$
. We only give proofs of the following four cases.
-
• If
 $\varphi $
is
$\varphi $
is
 $\forall \vec {x} \bigl (\Box (\psi (\vec {x}) \to \sigma (\vec {x})) \to (\Box \psi (\vec {x}) \to \Box \sigma (\vec {x})) \bigr )$
, then
$\forall \vec {x} \bigl (\Box (\psi (\vec {x}) \to \sigma (\vec {x})) \to (\Box \psi (\vec {x}) \to \Box \sigma (\vec {x})) \bigr )$
, then
 $\pi ^{\prime }_U(\varphi )$
is This sentence is provable in
$\pi ^{\prime }_U(\varphi )$
is This sentence is provable in $$ \begin{align*} & \forall \vec{x} \Bigl(\mathrm{Pr}_U(\ulcorner\psi(\vec{\dot{x}}) \to \sigma(\vec{\dot{x}})\urcorner) \land \pi^{\prime}_U(\psi(\vec{x}) \to \sigma(\vec{x}))\\ & \ \ \ \ \ \to \bigl(\bigl[\mathrm{Pr}_U(\ulcorner\psi(\vec{\dot{x}})\urcorner) \land \pi^{\prime}_U(\psi(\vec{x})) \bigr] \to \bigl[\mathrm{Pr}_U(\ulcorner\sigma(\vec{\dot{x}})\urcorner) \land \pi^{\prime}_U(\sigma(\vec{x})) \bigr] \bigr) \Bigr). \end{align*} $$
$$ \begin{align*} & \forall \vec{x} \Bigl(\mathrm{Pr}_U(\ulcorner\psi(\vec{\dot{x}}) \to \sigma(\vec{\dot{x}})\urcorner) \land \pi^{\prime}_U(\psi(\vec{x}) \to \sigma(\vec{x}))\\ & \ \ \ \ \ \to \bigl(\bigl[\mathrm{Pr}_U(\ulcorner\psi(\vec{\dot{x}})\urcorner) \land \pi^{\prime}_U(\psi(\vec{x})) \bigr] \to \bigl[\mathrm{Pr}_U(\ulcorner\sigma(\vec{\dot{x}})\urcorner) \land \pi^{\prime}_U(\sigma(\vec{x})) \bigr] \bigr) \Bigr). \end{align*} $$
 $\mathbf {PA}$
.
$\mathbf {PA}$
.
-
• If
 $\varphi $
is
$\varphi $
is
 $\forall \vec {x}(\Box \psi (\vec {x}) \to \psi (\vec {x}))$
, then
$\forall \vec {x}(\Box \psi (\vec {x}) \to \psi (\vec {x}))$
, then
 $\pi ^{\prime }_U(\varphi )$
is and this is obviously provable in
$\pi ^{\prime }_U(\varphi )$
is and this is obviously provable in $$\begin{align*}\forall \vec{x} \bigl(\mathrm{Pr}_U(\ulcorner\psi(\vec{\dot{x}})\urcorner) \land \pi^{\prime}_U(\psi(\vec{x})) \to \pi^{\prime}_U(\psi(\vec{x})) \bigr), \end{align*}$$
$$\begin{align*}\forall \vec{x} \bigl(\mathrm{Pr}_U(\ulcorner\psi(\vec{\dot{x}})\urcorner) \land \pi^{\prime}_U(\psi(\vec{x})) \to \pi^{\prime}_U(\psi(\vec{x})) \bigr), \end{align*}$$
 $\mathbf {PA}$
.
$\mathbf {PA}$
.
-
• If
 $\varphi $
is
$\varphi $
is
 $\forall \vec {x}(\Box \psi (\vec {x}) \to \Box \Box \psi (\vec {x}))$
, then
$\forall \vec {x}(\Box \psi (\vec {x}) \to \Box \Box \psi (\vec {x}))$
, then
 $\pi _U(\varphi )$
is and this is provable in
$\pi _U(\varphi )$
is and this is provable in $$\begin{align*}&\forall \vec{x} \Bigl(\bigl[\mathrm{Pr}_U(\ulcorner\psi(\vec{\dot{x}})\urcorner) \land \pi^{\prime}_U(\psi(\vec{x})) \bigr] \\&\quad\to \bigl[\mathrm{Pr}_U(\ulcorner\Box \psi(\vec{\dot{x}})\urcorner) \land \mathrm{Pr}_U(\ulcorner\psi(\vec{\dot{x}})\urcorner) \land \pi^{\prime}_U(\psi(\vec{x})) \bigr] \Bigr), \end{align*}$$
$$\begin{align*}&\forall \vec{x} \Bigl(\bigl[\mathrm{Pr}_U(\ulcorner\psi(\vec{\dot{x}})\urcorner) \land \pi^{\prime}_U(\psi(\vec{x})) \bigr] \\&\quad\to \bigl[\mathrm{Pr}_U(\ulcorner\Box \psi(\vec{\dot{x}})\urcorner) \land \mathrm{Pr}_U(\ulcorner\psi(\vec{\dot{x}})\urcorner) \land \pi^{\prime}_U(\psi(\vec{x})) \bigr] \Bigr), \end{align*}$$
 $\mathbf {PA}$
.
$\mathbf {PA}$
.
-
• If
 $\varphi (\vec {x})$
is derived from
$\varphi (\vec {x})$
is derived from
 $\psi (\vec {x})$
by Nec, then
$\psi (\vec {x})$
by Nec, then
 $\varphi (\vec {x}) \equiv \Box \psi (\vec {x})$
. Since
$\varphi (\vec {x}) \equiv \Box \psi (\vec {x})$
. Since
 $T \vdash \psi (\vec {x})$
, by the induction hypothesis,
$T \vdash \psi (\vec {x})$
, by the induction hypothesis,
 $\mathbf {PA} \vdash \pi ^{\prime }_U(\psi (\vec {x}))$
. Also,
$\mathbf {PA} \vdash \pi ^{\prime }_U(\psi (\vec {x}))$
. Also,
 $\mathbf {PA} \vdash \mathrm {Pr}_U(\ulcorner \psi (\vec {\dot {x}})\urcorner )$
because U is an extension of T. Thus,
$\mathbf {PA} \vdash \mathrm {Pr}_U(\ulcorner \psi (\vec {\dot {x}})\urcorner )$
because U is an extension of T. Thus,
 $\mathbf {PA} \vdash \pi ^{\prime }_U(\varphi (\vec {x}))$
.
$\mathbf {PA} \vdash \pi ^{\prime }_U(\varphi (\vec {x}))$
.
As in the proof of Proposition 6.47, we can prove the following proposition from Propositions 6.45 and 6.50.
Proposition 6.51 (Cf. [Reference Shapiro21, TB])
Let T be an
![]() $\mathcal {L}_A(\Box )$
-theory obtained by adding some axioms of
$\mathcal {L}_A(\Box )$
-theory obtained by adding some axioms of
![]() $\mathbf {PA}(\mathbf {S4})$
into
$\mathbf {PA}(\mathbf {S4})$
into
![]() $\mathbf {PA}_{\Box }$
, and let U be any r.e. extension of T. If
$\mathbf {PA}_{\Box }$
, and let U be any r.e. extension of T. If
![]() $\mathbb {N} \models \pi ^{\prime }_U(\varphi )$
for all
$\mathbb {N} \models \pi ^{\prime }_U(\varphi )$
for all
![]() $\varphi \in U \setminus T$
, then U is
$\varphi \in U \setminus T$
, then U is
![]() $\mathcal {L}_A(\Box )$
-sound.
$\mathcal {L}_A(\Box )$
-sound.
Corollary 6.52. The theories
![]() $\mathbf {PA}(\mathbf {KT})$
and
$\mathbf {PA}(\mathbf {KT})$
and
![]() $\mathbf {PA}(\mathbf {S4})$
are
$\mathbf {PA}(\mathbf {S4})$
are
![]() $\mathcal {L}_A(\Box )$
-sound.
$\mathcal {L}_A(\Box )$
-sound.
The alternative
![]() $\mathcal {L}_A(\Box )$
-soundness of
$\mathcal {L}_A(\Box )$
-soundness of
![]() $\mathbf {PA}(\mathbf {S4})$
is already proved by Shapiro [Reference Shapiro21, TB’].
$\mathbf {PA}(\mathbf {S4})$
is already proved by Shapiro [Reference Shapiro21, TB’].
Corollary 6.53. Let T be an r.e.
![]() $\mathcal {L}_A(\Box )$
-theory obtained by adding some axioms of
$\mathcal {L}_A(\Box )$
-theory obtained by adding some axioms of
![]() $\mathbf {PA}(\mathbf {S4}) + \{\Box \Diamond \varphi \to \varphi \mid \varphi $
is an
$\mathbf {PA}(\mathbf {S4}) + \{\Box \Diamond \varphi \to \varphi \mid \varphi $
is an
![]() $\mathcal {L}_A$
-sentence
$\mathcal {L}_A$
-sentence
![]() $\}$
into
$\}$
into
![]() $\mathbf {PA}_{\Box }$
. Then, T is
$\mathbf {PA}_{\Box }$
. Then, T is
![]() $\mathcal {L}_A(\Box )$
-sound.
$\mathcal {L}_A(\Box )$
-sound.
Proof. By Proposition 6.51, it suffices to show that for any
![]() $\mathcal {L}_A$
-sentence
$\mathcal {L}_A$
-sentence
![]() $\varphi $
, if
$\varphi $
, if
![]() $\Box \Diamond \varphi \to \varphi \in T$
, then
$\Box \Diamond \varphi \to \varphi \in T$
, then
![]() $\mathbb {N} \models \pi ^{\prime }_T(\Box \Diamond \varphi \to \varphi )$
. Suppose that
$\mathbb {N} \models \pi ^{\prime }_T(\Box \Diamond \varphi \to \varphi )$
. Suppose that
![]() $\Box \Diamond \varphi \to \varphi \in T$
and
$\Box \Diamond \varphi \to \varphi \in T$
and
![]() $\mathbb {N} \models \pi ^{\prime }_T(\Box \Diamond \varphi )$
. Then,
$\mathbb {N} \models \pi ^{\prime }_T(\Box \Diamond \varphi )$
. Then,
![]() $T \vdash \Diamond \varphi $
, and
$T \vdash \Diamond \varphi $
, and
![]() $T \vdash \Box \Diamond \varphi $
. Since
$T \vdash \Box \Diamond \varphi $
. Since
![]() $T \vdash \Box \Diamond \varphi \to \varphi $
, we have
$T \vdash \Box \Diamond \varphi \to \varphi $
, we have
![]() $T \vdash \varphi $
. Since T is a subtheory of
$T \vdash \varphi $
. Since T is a subtheory of
![]() $\mathbf {PA}(\mathbf {Triv})$
, T is an conservative extension of
$\mathbf {PA}(\mathbf {Triv})$
, T is an conservative extension of
![]() $\mathbf {PA}$
by Corollary 2.4. Then,
$\mathbf {PA}$
by Corollary 2.4. Then,
![]() $\mathbf {PA} \vdash \varphi $
because
$\mathbf {PA} \vdash \varphi $
because
![]() $\varphi $
is an
$\varphi $
is an
![]() $\mathcal {L}_A$
-sentence. By the
$\mathcal {L}_A$
-sentence. By the
![]() $\mathcal {L}_A$
-soundness of
$\mathcal {L}_A$
-soundness of
![]() $\mathbf {PA}$
, we have
$\mathbf {PA}$
, we have
![]() $\mathbb {N} \models \varphi $
and hence
$\mathbb {N} \models \varphi $
and hence
![]() $\mathbb {N} \models \pi _T'(\varphi )$
. We have proved
$\mathbb {N} \models \pi _T'(\varphi )$
. We have proved
![]() $\mathbb {N} \models \pi ^{\prime }_U(\Box \Diamond \varphi \to \varphi )$
.
$\mathbb {N} \models \pi ^{\prime }_U(\Box \Diamond \varphi \to \varphi )$
.
In contrast to Corollary 6.53, we have the following proposition which is a refinement of Proposition 4.28.1.
Proposition 6.54. Let T be a consistent r.e.
![]() $\mathcal {L}_A(\Box )$
-theory extending the theory
$\mathcal {L}_A(\Box )$
-theory extending the theory
![]() $\mathbf {PA}(\mathbf {KT}) + \{\Box \Diamond \varphi \to \varphi \mid \varphi \text { is a } \Sigma (\mathrm {B})\text {-sentence}\}$
. Then, T does not have
$\mathbf {PA}(\mathbf {KT}) + \{\Box \Diamond \varphi \to \varphi \mid \varphi \text { is a } \Sigma (\mathrm {B})\text {-sentence}\}$
. Then, T does not have
![]() $(\mathrm {B}, \Sigma _1)$
-
$(\mathrm {B}, \Sigma _1)$
-
![]() $\mathrm {DP}$
.
$\mathrm {DP}$
.
Proof. Let
![]() $\varphi $
be a
$\varphi $
be a
![]() $\Sigma _1$
sentence such that
$\Sigma _1$
sentence such that
![]() $T \nvdash \varphi $
and
$T \nvdash \varphi $
and
![]() $T \nvdash \neg \varphi $
. Then,
$T \nvdash \neg \varphi $
. Then,
![]() $T \nvdash \Box \neg \varphi $
because
$T \nvdash \Box \neg \varphi $
because
![]() $T \vdash \Box \neg \varphi \to \neg \varphi $
. Since
$T \vdash \Box \neg \varphi \to \neg \varphi $
. Since
![]() $T \vdash \Box \Diamond \varphi \to \Diamond \varphi $
, we have
$T \vdash \Box \Diamond \varphi \to \Diamond \varphi $
, we have
![]() $T \vdash \Diamond \Box \neg \varphi \lor \Diamond \varphi $
. Then,
$T \vdash \Diamond \Box \neg \varphi \lor \Diamond \varphi $
. Then,
![]() $T \vdash \Diamond (\Box \neg \varphi \lor \varphi )$
and hence
$T \vdash \Diamond (\Box \neg \varphi \lor \varphi )$
and hence
![]() $T \vdash \Box \Diamond (\Box \neg \varphi \lor \varphi )$
. Since
$T \vdash \Box \Diamond (\Box \neg \varphi \lor \varphi )$
. Since
![]() $\Box \neg \varphi \lor \varphi $
is a
$\Box \neg \varphi \lor \varphi $
is a
![]() $\Sigma (\mathrm {B})$
sentence, we obtain
$\Sigma (\mathrm {B})$
sentence, we obtain
![]() $T \vdash \Box \neg \varphi \lor \varphi $
because
$T \vdash \Box \neg \varphi \lor \varphi $
because
![]() $\Box \Diamond (\Box \neg \varphi \lor \varphi ) \to (\Box \neg \varphi \lor \varphi )$
is an axiom of T. We have shown that
$\Box \Diamond (\Box \neg \varphi \lor \varphi ) \to (\Box \neg \varphi \lor \varphi )$
is an axiom of T. We have shown that
![]() $T \nvdash \Box \neg \varphi $
,
$T \nvdash \Box \neg \varphi $
,
![]() $T \nvdash \varphi $
, and
$T \nvdash \varphi $
, and
![]() $T \vdash \Box \neg \varphi \lor \varphi $
. This means that T does not have
$T \vdash \Box \neg \varphi \lor \varphi $
. This means that T does not have
![]() $(\mathrm {B}, \Sigma _1)$
-
$(\mathrm {B}, \Sigma _1)$
-
![]() $\mathrm {DP}$
.
$\mathrm {DP}$
.
6.2
 $\Sigma (\mathrm {B})$
-soundness and weak
$\Sigma (\mathrm {B})$
-soundness and weak
 $\Sigma (\mathrm {B})$
-soundness
$\Sigma (\mathrm {B})$
-soundness
We then export the notion of the
![]() $\Sigma _1$
-soundness to modal arithmetic. This is easy to do since we have already introduced the class
$\Sigma _1$
-soundness to modal arithmetic. This is easy to do since we have already introduced the class
![]() $\Sigma (\mathrm {B})$
corresponding to
$\Sigma (\mathrm {B})$
corresponding to
![]() $\Sigma _1$
in modal arithmetic. Here we further introduce another type of translation
$\Sigma _1$
in modal arithmetic. Here we further introduce another type of translation
![]() $\rho _T$
, which is different from
$\rho _T$
, which is different from
![]() $\pi _T$
.
$\pi _T$
.
Definition 6.55 (
 $\rho $
-translations)
$\rho $
-translations)
Let T be any r.e.
![]() $\mathcal {L}_A(\Box )$
-theory. We define a translation
$\mathcal {L}_A(\Box )$
-theory. We define a translation
![]() $\rho _T$
of
$\rho _T$
of
![]() $\mathcal {L}_A(\Box )$
-formulas into
$\mathcal {L}_A(\Box )$
-formulas into
![]() $\mathcal {L}_A$
-formulas inductively as follows:
$\mathcal {L}_A$
-formulas inductively as follows:
-
1. If
 $\varphi $
is an
$\varphi $
is an
 $\mathcal {L}_A$
-formula, then
$\mathcal {L}_A$
-formula, then
 $\rho _T(\varphi ) : \equiv \varphi $
.
$\rho _T(\varphi ) : \equiv \varphi $
. -
2.
 $\rho _T$
preserves logical connectives and quantifiers.
$\rho _T$
preserves logical connectives and quantifiers. -
3.
 $\rho _T(\Box \varphi (\vec {x})) : \equiv \mathrm {Pr}_T(\ulcorner \Box \varphi (\vec {\dot {x}}) \urcorner )$
.
$\rho _T(\Box \varphi (\vec {x})) : \equiv \mathrm {Pr}_T(\ulcorner \Box \varphi (\vec {\dot {x}}) \urcorner )$
.
With respect to
![]() $\Sigma (\mathrm {B})$
sentences, there is the following relationship between the translations
$\Sigma (\mathrm {B})$
sentences, there is the following relationship between the translations
![]() $\pi _T$
and
$\pi _T$
and
![]() $\rho _T$
.
$\rho _T$
.
Proposition 6.56. Let T be any r.e.
![]() $\mathcal {L}_A(\Box )$
-theory.
$\mathcal {L}_A(\Box )$
-theory.
-
1. For any
 $\Sigma (\mathrm {B})$
-sentence
$\Sigma (\mathrm {B})$
-sentence
 $\varphi $
,
$\varphi $
,
 $\mathbb {N} \models \pi _T(\varphi ) \to \rho _T(\varphi )$
.
$\mathbb {N} \models \pi _T(\varphi ) \to \rho _T(\varphi )$
. -
2. If T is closed under the box elimination rule, then for any
 $\Sigma (\mathrm {B})$
-sentence
$\Sigma (\mathrm {B})$
-sentence
 $\varphi $
,
$\varphi $
,
 $\mathbb {N} \models \rho _T(\varphi ) \to \pi _T(\varphi )$
.
$\mathbb {N} \models \rho _T(\varphi ) \to \pi _T(\varphi )$
.
Proof. These statements are proved by induction on the construction of
![]() $\varphi $
. We only prove the case of
$\varphi $
. We only prove the case of
![]() $\varphi \equiv \Box \psi $
.
$\varphi \equiv \Box \psi $
.
1. If
![]() $\mathbb {N} \models \pi _T(\Box \psi )$
, then
$\mathbb {N} \models \pi _T(\Box \psi )$
, then
![]() $\mathbb {N} \models \mathrm {Pr}_T(\ulcorner \psi \urcorner )$
. Then,
$\mathbb {N} \models \mathrm {Pr}_T(\ulcorner \psi \urcorner )$
. Then,
![]() $T \vdash \psi $
. By the rule Nec,
$T \vdash \psi $
. By the rule Nec,
![]() $T \vdash \Box \psi $
. Then,
$T \vdash \Box \psi $
. Then,
![]() $\mathbb {N} \models \mathrm {Pr}_T(\ulcorner \Box \psi \urcorner )$
, and hence
$\mathbb {N} \models \mathrm {Pr}_T(\ulcorner \Box \psi \urcorner )$
, and hence
![]() $\mathbb {N} \models \rho _T(\Box \psi )$
.
$\mathbb {N} \models \rho _T(\Box \psi )$
.
2. If
![]() $\mathbb {N} \models \rho _T(\Box \psi )$
, then
$\mathbb {N} \models \rho _T(\Box \psi )$
, then
![]() $T \vdash \Box \psi $
. By the box elimination rule,
$T \vdash \Box \psi $
. By the box elimination rule,
![]() $T \vdash \psi $
. Hence,
$T \vdash \psi $
. Hence,
![]() $\mathbb {N} \models \pi _T(\Box \psi )$
.
$\mathbb {N} \models \pi _T(\Box \psi )$
.
We strengthen the usual
![]() $\Sigma _1$
-completeness theorem of
$\Sigma _1$
-completeness theorem of
![]() $\mathbf {PA}$
as follows.
$\mathbf {PA}$
as follows.
Theorem 6.57 (
 $\Sigma (\mathrm {B})$
-completeness theorem)
$\Sigma (\mathrm {B})$
-completeness theorem)
Let T be any r.e. extension of
![]() $\mathbf {PA}_{\Box }$
. Then, for any
$\mathbf {PA}_{\Box }$
. Then, for any
![]() $\Sigma (\mathrm {B})$
sentence
$\Sigma (\mathrm {B})$
sentence
![]() $\varphi $
, if
$\varphi $
, if
![]() $\mathbb {N} \models \rho _T(\varphi )$
, then
$\mathbb {N} \models \rho _T(\varphi )$
, then
![]() $T \vdash \varphi $
.
$T \vdash \varphi $
.
Proof. We prove the theorem by induction on the construction of
![]() $\varphi $
.
$\varphi $
.
-
• If
 $\varphi $
is a
$\varphi $
is a
 $\Sigma _1$
sentence, then the statement immediately follows from the usual
$\Sigma _1$
sentence, then the statement immediately follows from the usual
 $\Sigma _1$
-completeness of
$\Sigma _1$
-completeness of
 $\mathbf {PA}$
because
$\mathbf {PA}$
because
 $\rho _T(\varphi )$
is exactly
$\rho _T(\varphi )$
is exactly
 $\varphi $
.
$\varphi $
. -
• If
 $\varphi $
is of the form
$\varphi $
is of the form
 $\Box \psi $
, then
$\Box \psi $
, then
 $\mathbb {N} \models \rho _T(\Box \psi )$
means
$\mathbb {N} \models \rho _T(\Box \psi )$
means
 $\mathbb {N} \models \mathrm {Pr}_T(\ulcorner \Box \psi \urcorner )$
, and hence
$\mathbb {N} \models \mathrm {Pr}_T(\ulcorner \Box \psi \urcorner )$
, and hence
 $T \vdash \Box \psi $
.
$T \vdash \Box \psi $
. -
• If
 $\varphi $
is one of the forms
$\varphi $
is one of the forms
 $\psi \land \sigma $
,
$\psi \land \sigma $
,
 $\psi \lor \sigma $
,
$\psi \lor \sigma $
,
 $\exists x \psi $
, and
$\exists x \psi $
, and
 $\forall x < t \ \psi $
, then the proof is straightforward by the induction hypothesis.
$\forall x < t \ \psi $
, then the proof is straightforward by the induction hypothesis.
In the light of Proposition 6.56 and Theorem 6.57, we introduce the following two different types of the notion of
![]() $\Sigma (\mathrm {B})$
-soundness.
$\Sigma (\mathrm {B})$
-soundness.
Definition 6.58. Let T be any r.e.
![]() $\mathcal {L}_A(\Box )$
-theory.
$\mathcal {L}_A(\Box )$
-theory.
-
• T is said to be
 $\Sigma (\mathrm {B})$
-sound if for any
$\Sigma (\mathrm {B})$
-sound if for any
 $\Sigma (\mathrm {B})$
sentence
$\Sigma (\mathrm {B})$
sentence
 $\varphi $
, if
$\varphi $
, if
 $T \vdash \varphi $
, then
$T \vdash \varphi $
, then
 $\mathbb {N} \models \pi _T(\varphi )$
.
$\mathbb {N} \models \pi _T(\varphi )$
. -
• T is said to be weakly
 $\Sigma (\mathrm {B})$
-sound if for any
$\Sigma (\mathrm {B})$
-sound if for any
 $\Sigma (\mathrm {B})$
sentence
$\Sigma (\mathrm {B})$
sentence
 $\varphi $
, if
$\varphi $
, if
 $T \vdash \varphi $
, then
$T \vdash \varphi $
, then
 $\mathbb {N} \models \rho _T(\varphi )$
.
$\mathbb {N} \models \rho _T(\varphi )$
.
Lemma 6.59. For any r.e.
![]() $\mathcal {L}_A(\Box )$
-theory T, the following are equivalent:
$\mathcal {L}_A(\Box )$
-theory T, the following are equivalent:
-
1. T is
 $\Sigma (\mathrm {B})$
-sound.
$\Sigma (\mathrm {B})$
-sound. -
2. T is weakly
 $\Sigma (\mathrm {B})$
-sound and T is closed under the box elimination rule.
$\Sigma (\mathrm {B})$
-sound and T is closed under the box elimination rule.
Proof. By Proposition 6.56, it suffices to show that
![]() $\Sigma (\mathrm {B})$
-soundness implies the box elimination rule. Suppose that T is
$\Sigma (\mathrm {B})$
-soundness implies the box elimination rule. Suppose that T is
![]() $\Sigma (\mathrm {B})$
-sound. Let
$\Sigma (\mathrm {B})$
-sound. Let
![]() $\varphi $
be any
$\varphi $
be any
![]() $\mathcal {L}_A(\Box )$
-sentence such that
$\mathcal {L}_A(\Box )$
-sentence such that
![]() $T \vdash \Box \varphi $
. By the
$T \vdash \Box \varphi $
. By the
![]() $\Sigma (\mathrm {B})$
-soundness of T,
$\Sigma (\mathrm {B})$
-soundness of T,
![]() $\mathbb {N} \models \pi _T(\Box \varphi )$
and hence
$\mathbb {N} \models \pi _T(\Box \varphi )$
and hence
![]() $\mathbb {N} \models \mathrm {Pr}_T(\ulcorner \varphi \urcorner )$
. We obtain
$\mathbb {N} \models \mathrm {Pr}_T(\ulcorner \varphi \urcorner )$
. We obtain
![]() $T \vdash \varphi $
.
$T \vdash \varphi $
.
We are ready to prove an analogue of Guaspari’s theorem.
Theorem 6.60. Let T be an r.e. extension of
![]() $\mathbf {PA}_{\Box }$
.
$\mathbf {PA}_{\Box }$
.
-
1. If T contains
 $\mathbf {PA}(\mathbf {K})$
,
$\mathbf {PA}(\mathbf {K})$
,
 $T \nvdash \Box \bot $
, and T has
$T \nvdash \Box \bot $
, and T has
 $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
 $\mathrm {DP}$
, then T is weakly
$\mathrm {DP}$
, then T is weakly
 $\Sigma (\mathrm {B})$
-sound.
$\Sigma (\mathrm {B})$
-sound. -
2. If T is weakly
 $\Sigma (\mathrm {B})$
-sound, then T has
$\Sigma (\mathrm {B})$
-sound, then T has
 $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
 $\mathrm {EP}$
.
$\mathrm {EP}$
.
Proof. 1. We prove by induction on the construction of
![]() $\varphi $
that for any
$\varphi $
that for any
![]() $\Sigma (\mathrm {B})$
sentence
$\Sigma (\mathrm {B})$
sentence
![]() $\varphi $
, if
$\varphi $
, if
![]() $T \vdash \varphi $
, then
$T \vdash \varphi $
, then
![]() $\mathbb {N} \models \rho _T(\varphi )$
.
$\mathbb {N} \models \rho _T(\varphi )$
.
-
• If
 $\varphi $
is a
$\varphi $
is a
 $\Sigma _1$
sentence, then
$\Sigma _1$
sentence, then
 $\rho _T(\varphi ) \equiv \varphi $
. Suppose
$\rho _T(\varphi ) \equiv \varphi $
. Suppose
 $T \vdash \varphi $
. Since
$T \vdash \varphi $
. Since
 $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
 $\mathrm {DP}$
implies
$\mathrm {DP}$
implies
 $(\mathrm {B}, \Sigma _1)$
-
$(\mathrm {B}, \Sigma _1)$
-
 $\mathrm {DP}$
, T is
$\mathrm {DP}$
, T is
 $\Sigma _1$
-sound by Proposition 4.21. Therefore,
$\Sigma _1$
-sound by Proposition 4.21. Therefore,
 $\mathbb {N} \models \rho _T(\varphi )$
.
$\mathbb {N} \models \rho _T(\varphi )$
. -
• If
 $\varphi $
is of the form
$\varphi $
is of the form
 $\Box \psi $
, then
$\Box \psi $
, then
 $\rho _T(\varphi ) \equiv \mathrm {Pr}_T(\ulcorner \Box \psi \urcorner )$
. Suppose
$\rho _T(\varphi ) \equiv \mathrm {Pr}_T(\ulcorner \Box \psi \urcorner )$
. Suppose
 $T \vdash \Box \psi $
. Then, obviously
$T \vdash \Box \psi $
. Then, obviously
 $\mathbb {N} \models \rho _T(\varphi )$
.
$\mathbb {N} \models \rho _T(\varphi )$
. -
• If
 $\varphi $
is of the form
$\varphi $
is of the form
 $\psi \land \sigma $
or
$\psi \land \sigma $
or
 $\forall x < t\, \psi $
, then the proof is straightforward from the induction hypothesis.
$\forall x < t\, \psi $
, then the proof is straightforward from the induction hypothesis. -
• If
 $\varphi $
is
$\varphi $
is
 $\psi \lor \sigma $
, then
$\psi \lor \sigma $
, then
 $\rho _T(\varphi ) \equiv \rho _T(\psi ) \lor \rho _T(\sigma )$
. Suppose
$\rho _T(\varphi ) \equiv \rho _T(\psi ) \lor \rho _T(\sigma )$
. Suppose
 $T \vdash \psi \lor \sigma $
. Then, by
$T \vdash \psi \lor \sigma $
. Then, by
 $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
 $\mathrm {DP}$
,
$\mathrm {DP}$
,
 $T \vdash \psi $
or
$T \vdash \psi $
or
 $T \vdash \sigma $
. By the induction hypothesis,
$T \vdash \sigma $
. By the induction hypothesis,
 $\mathbb {N} \models \rho _T(\psi )$
or
$\mathbb {N} \models \rho _T(\psi )$
or
 $\mathbb {N} \models \rho _T(\sigma )$
. Hence,
$\mathbb {N} \models \rho _T(\sigma )$
. Hence,
 $\mathbb {N} \models \rho _T(\varphi )$
.
$\mathbb {N} \models \rho _T(\varphi )$
. -
• If
 $\varphi $
is
$\varphi $
is
 $\exists x \psi (x)$
, then
$\exists x \psi (x)$
, then
 $\rho _T(\varphi ) \equiv \exists x \rho _T(\psi (x))$
. Suppose
$\rho _T(\varphi ) \equiv \exists x \rho _T(\psi (x))$
. Suppose
 $T \vdash \exists x \psi (x)$
. Since
$T \vdash \exists x \psi (x)$
. Since
 $T \nvdash \Box \bot $
, by Theorem 5.38, T has
$T \nvdash \Box \bot $
, by Theorem 5.38, T has
 $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
 $\mathrm {EP}$
. Then, there exists a natural number
$\mathrm {EP}$
. Then, there exists a natural number
 $n$
such that
$n$
such that
 $T \vdash \psi (\overline {n})$
. By the induction hypothesis,
$T \vdash \psi (\overline {n})$
. By the induction hypothesis,
 $\mathbb {N} \models \rho _T(\psi (\overline {n}))$
. Therefore,
$\mathbb {N} \models \rho _T(\psi (\overline {n}))$
. Therefore,
 $\mathbb {N} \models \rho _T(\varphi )$
.
$\mathbb {N} \models \rho _T(\varphi )$
.
2. Let
![]() $\varphi (x)$
be any
$\varphi (x)$
be any
![]() $\Sigma (\mathrm {B})$
formula having no free variables except
$\Sigma (\mathrm {B})$
formula having no free variables except
![]() $x$
such that
$x$
such that
![]() $T \vdash \exists x \varphi (x)$
. By the weak
$T \vdash \exists x \varphi (x)$
. By the weak
![]() $\Sigma (\mathrm {B})$
-soundness of T,
$\Sigma (\mathrm {B})$
-soundness of T,
![]() $\mathbb {N} \models \rho _T(\exists x \varphi (x))$
. Then, for some natural number
$\mathbb {N} \models \rho _T(\exists x \varphi (x))$
. Then, for some natural number
![]() $n$
,
$n$
,
![]() $\mathbb {N} \models \rho _T(\varphi (\overline {n}))$
. By Theorem 6.57,
$\mathbb {N} \models \rho _T(\varphi (\overline {n}))$
. By Theorem 6.57,
![]() $T \vdash \varphi (\overline {n})$
.
$T \vdash \varphi (\overline {n})$
.
Corollary 6.61. Let T be an r.e. extension of
![]() $\mathbf {PA}_{\Box }$
.
$\mathbf {PA}_{\Box }$
.
-
1. If T contains
 $\mathbf {PA}(\mathbf {K4})$
, T is consistent, and T has
$\mathbf {PA}(\mathbf {K4})$
, T is consistent, and T has
 $\mathrm {MDP}$
, then T is
$\mathrm {MDP}$
, then T is
 $\Sigma (\mathrm {B})$
-sound.
$\Sigma (\mathrm {B})$
-sound. -
2. If T is
 $\Sigma (\mathrm {B})$
-sound, then T has
$\Sigma (\mathrm {B})$
-sound, then T has
 $\mathrm {MEP}$
.
$\mathrm {MEP}$
.
Proof. 1. Since T contains
![]() $\mathbf {PA}(\mathbf {K4})$
and T has
$\mathbf {PA}(\mathbf {K4})$
and T has
![]() $\mathrm {MDP}$
, by Proposition 5.39, T has
$\mathrm {MDP}$
, by Proposition 5.39, T has
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {DP}$
. Also, T is closed under the box elimination rule by Proposition 4.17. Then,
$\mathrm {DP}$
. Also, T is closed under the box elimination rule by Proposition 4.17. Then,
![]() $T \nvdash \Box \bot $
by the consistency of T. By Theorem 6.60.1, T is weakly
$T \nvdash \Box \bot $
by the consistency of T. By Theorem 6.60.1, T is weakly
![]() $\Sigma (\mathrm {B})$
-sound. By Lemma 6.59, T is
$\Sigma (\mathrm {B})$
-sound. By Lemma 6.59, T is
![]() $\Sigma (\mathrm {B})$
-sound.
$\Sigma (\mathrm {B})$
-sound.
2. By Lemma 6.59, T is weakly
![]() $\Sigma (\mathrm {B})$
-sound and is closed under the box elimination rule. By Theorem 6.60.2, T has
$\Sigma (\mathrm {B})$
-sound and is closed under the box elimination rule. By Theorem 6.60.2, T has
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {EP}$
. Therefore, by Proposition 4.17, T has
$\mathrm {EP}$
. Therefore, by Proposition 4.17, T has
![]() $\mathrm {MEP}$
.
$\mathrm {MEP}$
.
Since the
![]() $\mathcal {L}_A(\Box )$
-soundness implies the
$\mathcal {L}_A(\Box )$
-soundness implies the
![]() $\Sigma (\mathrm {B})$
-soundness, we obtain the following corollary from Propositions 6.47 and 6.51.
$\Sigma (\mathrm {B})$
-soundness, we obtain the following corollary from Propositions 6.47 and 6.51.
Corollary 6.62.
-
1. Let T be an
 $\mathcal {L}_A(\Box )$
-theory obtained by adding some axioms of
$\mathcal {L}_A(\Box )$
-theory obtained by adding some axioms of
 $\mathbf {PA}(\mathbf {GL})$
into
$\mathbf {PA}(\mathbf {GL})$
into
 $\mathbf {PA}_{\Box }$
, and let U be any r.e. extension of T. If
$\mathbf {PA}_{\Box }$
, and let U be any r.e. extension of T. If
 $\mathbb {N} \models \pi _U(\varphi )$
for all
$\mathbb {N} \models \pi _U(\varphi )$
for all
 $\varphi \in U \setminus T$
, then U has
$\varphi \in U \setminus T$
, then U has
 $\mathrm {MEP}$
.
$\mathrm {MEP}$
. -
2. Let T be an
 $\mathcal {L}_A(\Box )$
-theory obtained by adding some axioms of
$\mathcal {L}_A(\Box )$
-theory obtained by adding some axioms of
 $\mathbf {PA}(\mathbf {S4})$
into
$\mathbf {PA}(\mathbf {S4})$
into
 $\mathbf {PA}_{\Box }$
, and let U be any r.e. extension of T. If
$\mathbf {PA}_{\Box }$
, and let U be any r.e. extension of T. If
 $\mathbb {N} \models \pi ^{\prime }_U(\varphi )$
for all
$\mathbb {N} \models \pi ^{\prime }_U(\varphi )$
for all
 $\varphi \in U \setminus T$
, then U has
$\varphi \in U \setminus T$
, then U has
 $\mathrm {MEP}$
.
$\mathrm {MEP}$
.
In particular,
![]() $\mathbf {PA}_{\Box }$
,
$\mathbf {PA}_{\Box }$
,
![]() $\mathbf {PA}(\mathbf {K})$
,
$\mathbf {PA}(\mathbf {K})$
,
![]() $\mathbf {PA}(\mathbf {KT})$
,
$\mathbf {PA}(\mathbf {KT})$
,
![]() $\mathbf {PA}(\mathbf {K4})$
,
$\mathbf {PA}(\mathbf {K4})$
,
![]() $\mathbf {PA}(\mathbf {S4})$
, and
$\mathbf {PA}(\mathbf {S4})$
, and
![]() $\mathbf {PA}(\mathbf {GL})$
have
$\mathbf {PA}(\mathbf {GL})$
have
![]() $\mathrm {MEP}$
.
$\mathrm {MEP}$
.
By Lemma 6.59, each
![]() $\Sigma (\mathrm {B})$
-sound theory is also weakly
$\Sigma (\mathrm {B})$
-sound theory is also weakly
![]() $\Sigma (\mathrm {B})$
-sound. Therefore,
$\Sigma (\mathrm {B})$
-sound. Therefore,
![]() $\mathbf {PA}_{\Box }$
,
$\mathbf {PA}_{\Box }$
,
![]() $\mathbf {PA}(\mathbf {K})$
,
$\mathbf {PA}(\mathbf {K})$
,
![]() $\mathbf {PA}(\mathbf {KT})$
,
$\mathbf {PA}(\mathbf {KT})$
,
![]() $\mathbf {PA}(\mathbf {K4})$
,
$\mathbf {PA}(\mathbf {K4})$
,
![]() $\mathbf {PA}(\mathbf {S4})$
, and
$\mathbf {PA}(\mathbf {S4})$
, and
![]() $\mathbf {PA}(\mathbf {GL})$
also have
$\mathbf {PA}(\mathbf {GL})$
also have
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {EP}$
. Recall that
$\mathrm {EP}$
. Recall that
![]() $\mathbf {PA}(\mathbf {Verum})$
also has
$\mathbf {PA}(\mathbf {Verum})$
also has
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {EP}$
(Corollary 5.30).
$\mathrm {EP}$
(Corollary 5.30).
Here we give another sufficient condition for a theory to have
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {EP}$
. First, we prove an analogue of Proposition 6.46 with respect to
$\mathrm {EP}$
. First, we prove an analogue of Proposition 6.46 with respect to
![]() $\rho $
-translations.
$\rho $
-translations.
Proposition 6.63. Let T be any
![]() $\mathcal {L}_A(\Box )$
-theory obtained by adding some axioms of the form
$\mathcal {L}_A(\Box )$
-theory obtained by adding some axioms of the form
![]() $\forall \vec {x}(\Box \psi _0 \land \cdots \land \Box \psi _{k-1} \to \Box \psi _k)$
into
$\forall \vec {x}(\Box \psi _0 \land \cdots \land \Box \psi _{k-1} \to \Box \psi _k)$
into
![]() $\mathbf {PA}_{\Box }$
. Then, for any
$\mathbf {PA}_{\Box }$
. Then, for any
![]() $\mathcal {L}_A(\Box )$
-formula
$\mathcal {L}_A(\Box )$
-formula
![]() $\varphi $
, if
$\varphi $
, if
![]() $T \vdash \varphi $
, then for any r.e. extension U of T,
$T \vdash \varphi $
, then for any r.e. extension U of T,
![]() $\mathbf {PA} \vdash \rho _U(\varphi )$
.
$\mathbf {PA} \vdash \rho _U(\varphi )$
.
Proof. Let U be any r.e. extension of T. As in the proof of Proposition 2.3, we prove by induction on the length of proofs of
![]() $\varphi $
in T that for any
$\varphi $
in T that for any
![]() $\mathcal {L}_A(\Box )$
-formula
$\mathcal {L}_A(\Box )$
-formula
![]() $\varphi $
, if
$\varphi $
, if
![]() $T \vdash \varphi $
, then
$T \vdash \varphi $
, then
![]() $\mathbf {PA} \vdash \rho _U(\varphi )$
. We only give proofs of the following two cases.
$\mathbf {PA} \vdash \rho _U(\varphi )$
. We only give proofs of the following two cases.
-
• The case
 $\varphi \equiv \forall \vec {x} \bigl (\Box \psi _0(\vec {x}) \land \cdots \land \Box \psi _{k-1}(\vec {x}) \to \Box \psi _k(\vec {x}) \bigr )$
: Since U is an extension of T, we have
$\varphi \equiv \forall \vec {x} \bigl (\Box \psi _0(\vec {x}) \land \cdots \land \Box \psi _{k-1}(\vec {x}) \to \Box \psi _k(\vec {x}) \bigr )$
: Since U is an extension of T, we have
 $\mathbf {PA} \vdash \forall \vec {x} \, \mathrm {Pr}_U(\ulcorner \Box \psi _0(\vec {\dot {x}}) \land \cdots \land \Box \psi _{k-1}(\vec {\dot {x}}) \to \Box \psi _k(\vec {\dot {x}})\urcorner )$
, and hence
$\mathbf {PA} \vdash \forall \vec {x} \, \mathrm {Pr}_U(\ulcorner \Box \psi _0(\vec {\dot {x}}) \land \cdots \land \Box \psi _{k-1}(\vec {\dot {x}}) \to \Box \psi _k(\vec {\dot {x}})\urcorner )$
, and hence
 $\mathbf {PA}$
proves This sentence is exactly
$\mathbf {PA}$
proves This sentence is exactly $$\begin{align*}\forall \vec{x} \bigl(\mathrm{Pr}_U(\ulcorner\Box \psi_0(\vec{\dot{x}})\urcorner) \land \cdots \land \mathrm{Pr}_U(\ulcorner\Box \psi_{k-1}(\vec{\dot{x}})\urcorner) \to \mathrm{Pr}_U(\ulcorner\Box \psi_k(\vec{\dot{x}})\urcorner) \bigr). \end{align*}$$
$$\begin{align*}\forall \vec{x} \bigl(\mathrm{Pr}_U(\ulcorner\Box \psi_0(\vec{\dot{x}})\urcorner) \land \cdots \land \mathrm{Pr}_U(\ulcorner\Box \psi_{k-1}(\vec{\dot{x}})\urcorner) \to \mathrm{Pr}_U(\ulcorner\Box \psi_k(\vec{\dot{x}})\urcorner) \bigr). \end{align*}$$
 $\rho _U(\varphi )$
.
$\rho _U(\varphi )$
.
-
• If
 $\varphi (\vec {x})$
is derived from
$\varphi (\vec {x})$
is derived from
 $\psi (\vec {x})$
by Nec, then
$\psi (\vec {x})$
by Nec, then
 $\varphi (\vec {x}) \equiv \Box \psi (\vec {x})$
. Since
$\varphi (\vec {x}) \equiv \Box \psi (\vec {x})$
. Since
 $T \vdash \Box \psi (\vec {x})$
,
$T \vdash \Box \psi (\vec {x})$
,
 $U \vdash \Box \psi (\vec {x})$
, and hence
$U \vdash \Box \psi (\vec {x})$
, and hence
 $\mathbf {PA} \vdash \mathrm {Pr}_U(\ulcorner \Box \psi (\vec {\dot {x}})\urcorner )$
. Thus,
$\mathbf {PA} \vdash \mathrm {Pr}_U(\ulcorner \Box \psi (\vec {\dot {x}})\urcorner )$
. Thus,
 $\mathbf {PA} \vdash \rho _U(\varphi (\vec {x}))$
.
$\mathbf {PA} \vdash \rho _U(\varphi (\vec {x}))$
.
Corollary 6.64. Let T be any
![]() $\mathcal {L}_A(\Box )$
-theory obtained by adding some axioms of the form
$\mathcal {L}_A(\Box )$
-theory obtained by adding some axioms of the form
![]() $\forall \vec {x}(\Box \psi _0 \land \cdots \land \Box \psi _{k-1} \to \Box \psi _k)$
into
$\forall \vec {x}(\Box \psi _0 \land \cdots \land \Box \psi _{k-1} \to \Box \psi _k)$
into
![]() $\mathbf {PA}_{\Box }$
, and let U be any r.e. extension of T. If
$\mathbf {PA}_{\Box }$
, and let U be any r.e. extension of T. If
![]() $\mathbb {N} \models \rho _U(\varphi )$
for all
$\mathbb {N} \models \rho _U(\varphi )$
for all
![]() $\varphi \in U \setminus T$
, then U has
$\varphi \in U \setminus T$
, then U has
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {EP}$
.
$\mathrm {EP}$
.
6.3 Applications
In this subsection, as applications of our results we have obtained so far, we show two non-implications between the properties. Corollary 5.30 shows that in general,
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {DP}$
does not imply
$\mathrm {DP}$
does not imply
![]() $\mathrm {MDP}$
. The first application shows that this is also true for theories that do not contain
$\mathrm {MDP}$
. The first application shows that this is also true for theories that do not contain
![]() $\mathbf {PA}(\mathbf {Verum})$
.
$\mathbf {PA}(\mathbf {Verum})$
.
Proposition 6.65.
-
1. There exists an r.e. theory T such that
 $\mathbf {PA}(\mathbf {S4}) \vdash T \vdash \mathbf {PA}(\mathbf {K4})$
,
$\mathbf {PA}(\mathbf {S4}) \vdash T \vdash \mathbf {PA}(\mathbf {K4})$
,
 $T \nvdash \Box \bot $
, T has
$T \nvdash \Box \bot $
, T has
 $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
 $\mathrm {EP}$
, and T does not have
$\mathrm {EP}$
, and T does not have
 $\mathrm {MDP}$
;
$\mathrm {MDP}$
; -
2. There exists an r.e. theory T such that
 $\mathbf {PA}(\mathbf {Verum}) \vdash T \vdash \mathbf {PA}(\mathbf {GL})$
,
$\mathbf {PA}(\mathbf {Verum}) \vdash T \vdash \mathbf {PA}(\mathbf {GL})$
,
 $T \nvdash \Box \bot $
, T has
$T \nvdash \Box \bot $
, T has
 $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
 $\mathrm {EP}$
, and T does not have
$\mathrm {EP}$
, and T does not have
 $\mathrm {MDP}$
.
$\mathrm {MDP}$
.
Proof. 1. Let T be the theory
![]() $\mathbf {PA}(\mathbf {K4}) + \{\Box \neg \Box \bot \}$
. Since T is a subtheory of
$\mathbf {PA}(\mathbf {K4}) + \{\Box \neg \Box \bot \}$
. Since T is a subtheory of
![]() $\mathbf {PA}(\mathbf {Triv})$
, we have
$\mathbf {PA}(\mathbf {Triv})$
, we have
![]() $T \nvdash \Box \bot $
. By Corollary 6.64, T has
$T \nvdash \Box \bot $
. By Corollary 6.64, T has
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {EP}$
. Suppose, towards a contradiction, that
$\mathrm {EP}$
. Suppose, towards a contradiction, that
![]() $T \vdash \neg \Box \bot $
. Then, by the
$T \vdash \neg \Box \bot $
. Then, by the
![]() $\Sigma (\mathrm {B})$
-deduction theorem (Corollary 3.14),
$\Sigma (\mathrm {B})$
-deduction theorem (Corollary 3.14),
![]() $\mathbf {PA}(\mathbf {K4}) \vdash \Box \neg \Box \bot \to \neg \Box \bot $
. Then,
$\mathbf {PA}(\mathbf {K4}) \vdash \Box \neg \Box \bot \to \neg \Box \bot $
. Then,
![]() $\mathbf {PA}(\mathbf {Verum}) \vdash \Box \neg \Box \bot \to \neg \Box \bot $
. Since
$\mathbf {PA}(\mathbf {Verum}) \vdash \Box \neg \Box \bot \to \neg \Box \bot $
. Since
![]() $\mathbf {PA}(\mathbf {Verum}) \vdash \Box \neg \Box \bot \land \Box \bot $
, this contradicts the consistency of
$\mathbf {PA}(\mathbf {Verum}) \vdash \Box \neg \Box \bot \land \Box \bot $
, this contradicts the consistency of
![]() $\mathbf {PA}(\mathbf {Verum})$
. Therefore,
$\mathbf {PA}(\mathbf {Verum})$
. Therefore,
![]() $T \nvdash \neg \Box \bot $
. Since
$T \nvdash \neg \Box \bot $
. Since
![]() $T \vdash \Box \neg \Box \bot $
, T does not have
$T \vdash \Box \neg \Box \bot $
, T does not have
![]() $\mathrm {MDP}$
.
$\mathrm {MDP}$
.
2. Let
![]() $T: = \mathbf {PA}(\mathbf {GL}) + \{\Box \Box \bot \}$
. By Corollary 6.64, T has
$T: = \mathbf {PA}(\mathbf {GL}) + \{\Box \Box \bot \}$
. By Corollary 6.64, T has
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {EP}$
. Suppose, towards a contradiction, that T proves
$\mathrm {EP}$
. Suppose, towards a contradiction, that T proves
![]() $\Box \bot $
. By the
$\Box \bot $
. By the
![]() $\Sigma (\mathrm {B})$
-deduction theorem,
$\Sigma (\mathrm {B})$
-deduction theorem,
![]() $\mathbf {PA}(\mathbf {GL}) \vdash \Box \Box \bot \to \Box \bot $
. Then,
$\mathbf {PA}(\mathbf {GL}) \vdash \Box \Box \bot \to \Box \bot $
. Then,
![]() $\mathbf {PA}(\mathbf {GL}) \vdash \Box (\Box \Box \bot \to \Box \bot )$
and hence
$\mathbf {PA}(\mathbf {GL}) \vdash \Box (\Box \Box \bot \to \Box \bot )$
and hence
![]() $\mathbf {PA}(\mathbf {GL}) \vdash \Box \Box \bot $
. By
$\mathbf {PA}(\mathbf {GL}) \vdash \Box \Box \bot $
. By
![]() $\mathrm {MDP}$
of
$\mathrm {MDP}$
of
![]() $\mathbf {PA}(\mathbf {GL})$
(Corollary 6.62 and Proposition 4.18.1),
$\mathbf {PA}(\mathbf {GL})$
(Corollary 6.62 and Proposition 4.18.1),
![]() $\mathbf {PA}(\mathbf {GL}) \vdash \bot $
. This is a contradiction. Therefore,
$\mathbf {PA}(\mathbf {GL}) \vdash \bot $
. This is a contradiction. Therefore,
![]() $T \nvdash \Box \bot $
. Since
$T \nvdash \Box \bot $
. Since
![]() $T \vdash \Box \Box \bot $
, T does not have
$T \vdash \Box \Box \bot $
, T does not have
![]() $\mathrm {MDP}$
.
$\mathrm {MDP}$
.
Unlike the notion of the soundness of
![]() $\mathcal {L}_A$
-theories, Proposition 6.65.1 shows that the
$\mathcal {L}_A$
-theories, Proposition 6.65.1 shows that the
![]() $\mathcal {L}_A(\Box )$
-soundness is not preserved by taking a subtheory because
$\mathcal {L}_A(\Box )$
-soundness is not preserved by taking a subtheory because
![]() $\mathbf {PA}(\mathbf {S4})$
is
$\mathbf {PA}(\mathbf {S4})$
is
![]() $\mathcal {L}_A(\Box )$
-sound but T is not
$\mathcal {L}_A(\Box )$
-sound but T is not
![]() $\Sigma (\mathrm {B})$
-sound.
$\Sigma (\mathrm {B})$
-sound.
The second application shows that
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {DC}$
does not imply
$\mathrm {DC}$
does not imply
![]() $\mathrm {B}$
-
$\mathrm {B}$
-
![]() $\mathrm {DP}$
in general.
$\mathrm {DP}$
in general.
Proposition 6.66. There exists a consistent r.e. extension T of
![]() $\mathbf {PA}(\mathbf {K4})$
satisfying the following two conditions:
$\mathbf {PA}(\mathbf {K4})$
satisfying the following two conditions:
-
1. T is
 $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
 $\mathrm {DC}$
.
$\mathrm {DC}$
. -
2. T does not have
 $\mathrm {B}$
-
$\mathrm {B}$
-
 $\mathrm {DP}$
.
$\mathrm {DP}$
.
Proof. Let
![]() $\varphi $
be a Gödel sentence of
$\varphi $
be a Gödel sentence of
![]() $\mathbf {PA}$
. Let
$\mathbf {PA}$
. Let
![]() $T : = \mathbf {PA}(\mathbf {K4}) + \{\Box \varphi \lor \Box \neg \varphi \}$
,
$T : = \mathbf {PA}(\mathbf {K4}) + \{\Box \varphi \lor \Box \neg \varphi \}$
,
![]() $T_0 : = \mathbf {PA}(\mathbf {K4}) + \{\Box \varphi \}$
, and
$T_0 : = \mathbf {PA}(\mathbf {K4}) + \{\Box \varphi \}$
, and
![]() $T_1 : = \mathbf {PA}(\mathbf {K4}) + \{\Box \neg \varphi \}$
. By the
$T_1 : = \mathbf {PA}(\mathbf {K4}) + \{\Box \neg \varphi \}$
. By the
![]() $\Sigma (\mathrm {B})$
-deduction theorem, it is shown that for any
$\Sigma (\mathrm {B})$
-deduction theorem, it is shown that for any
![]() $\mathcal {L}_A(\Box )$
-formula
$\mathcal {L}_A(\Box )$
-formula
![]() $\psi $
,
$\psi $
,
Suppose, towards a contradiction,
![]() $T_0 \vdash \Box \bot $
. By the
$T_0 \vdash \Box \bot $
. By the
![]() $\Sigma (\mathrm {B})$
-deduction theorem,
$\Sigma (\mathrm {B})$
-deduction theorem,
![]() $\mathbf {PA}(\mathbf {K4})$
proves
$\mathbf {PA}(\mathbf {K4})$
proves
![]() $\Box \varphi \to \Box \bot $
. Since this is also provable in
$\Box \varphi \to \Box \bot $
. Since this is also provable in
![]() $\mathbf {PA}(\mathbf {Triv})$
, by Proposition 2.3, we have
$\mathbf {PA}(\mathbf {Triv})$
, by Proposition 2.3, we have
![]() $\mathbf {PA} \vdash \alpha (\Box \varphi ) \to \alpha (\Box \bot )$
. Then,
$\mathbf {PA} \vdash \alpha (\Box \varphi ) \to \alpha (\Box \bot )$
. Then,
![]() $\mathbf {PA} \vdash \neg \varphi $
, a contradiction. Similarly, we can prove
$\mathbf {PA} \vdash \neg \varphi $
, a contradiction. Similarly, we can prove
![]() $T_1 \nvdash \Box \bot $
.
$T_1 \nvdash \Box \bot $
.
1. Let
![]() $\psi $
be any
$\psi $
be any
![]() $\Sigma (\mathrm {B})$
sentence such that
$\Sigma (\mathrm {B})$
sentence such that
![]() $T \vdash \psi \lor \mathrm {Pr}_T(\ulcorner \psi \urcorner )$
. Then, for
$T \vdash \psi \lor \mathrm {Pr}_T(\ulcorner \psi \urcorner )$
. Then, for
![]() $i \in \{0, 1\}$
,
$i \in \{0, 1\}$
,
![]() $T_i \vdash \psi \lor \mathrm {Pr}_T(\ulcorner \psi \urcorner )$
by (6). By Corollary 6.64,
$T_i \vdash \psi \lor \mathrm {Pr}_T(\ulcorner \psi \urcorner )$
by (6). By Corollary 6.64,
![]() $T_i$
has
$T_i$
has
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {EP}$
, and hence has
$\mathrm {EP}$
, and hence has
![]() $(\Sigma (\mathrm {B}), \Sigma _1)$
-
$(\Sigma (\mathrm {B}), \Sigma _1)$
-
![]() $\mathrm {DP}$
. By Corollary 5.32,
$\mathrm {DP}$
. By Corollary 5.32,
![]() $T_i$
is
$T_i$
is
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {DC}$
. Therefore,
$\mathrm {DC}$
. Therefore,
![]() $T_i \vdash \psi $
. By (6), we obtain
$T_i \vdash \psi $
. By (6), we obtain
![]() $T \vdash \psi $
. Thus, T is also
$T \vdash \psi $
. Thus, T is also
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {DC}$
.
$\mathrm {DC}$
.
2. If
![]() $T \vdash \Box \neg \varphi $
or
$T \vdash \Box \neg \varphi $
or
![]() $T \vdash \Box \varphi $
, then
$T \vdash \Box \varphi $
, then
![]() $T_0 \vdash \Box \bot $
or
$T_0 \vdash \Box \bot $
or
![]() $T_1 \vdash \Box \bot $
by (6). This is a contradiction. Therefore,
$T_1 \vdash \Box \bot $
by (6). This is a contradiction. Therefore,
![]() $T \nvdash \Box \neg \varphi $
and
$T \nvdash \Box \neg \varphi $
and
![]() $T \nvdash \Box \varphi $
. On the other hand,
$T \nvdash \Box \varphi $
. On the other hand,
![]() $T \vdash \Box \varphi \lor \Box \neg \varphi $
. Thus, T does not have
$T \vdash \Box \varphi \lor \Box \neg \varphi $
. Thus, T does not have
![]() $\mathrm {B}$
-
$\mathrm {B}$
-
![]() $\mathrm {DP}$
.
$\mathrm {DP}$
.
7 Problems
In the present paper, several properties related to the modal disjunction property in modal arithmetic are introduced, and the relationships between them are studied. However, some of the properties have not yet been separated in some particular situation. In this section, we list several unsolved problems for further study.
In Section 4, we introduced
![]() $\mathrm {B}$
-
$\mathrm {B}$
-
![]() $\mathrm {DP}$
and
$\mathrm {DP}$
and
![]() $\Delta (\mathrm {B})$
-
$\Delta (\mathrm {B})$
-
![]() $\mathrm {DP}$
. For theories which are closed under the box elimination rule, these properties are equivalent. However, we have not yet been successful in clarifying whether they are equivalent or not in general. We propose the following problem.
$\mathrm {DP}$
. For theories which are closed under the box elimination rule, these properties are equivalent. However, we have not yet been successful in clarifying whether they are equivalent or not in general. We propose the following problem.
Problem 7.67.
-
1. Does there exist an
 $\mathcal {L}_A(\Box )$
-theory which has
$\mathcal {L}_A(\Box )$
-theory which has
 $\Delta (\mathrm {B})$
-
$\Delta (\mathrm {B})$
-
 $\mathrm {DP}$
but does not have
$\mathrm {DP}$
but does not have
 $\mathrm {B}$
-
$\mathrm {B}$
-
 $\mathrm {DP}$
?
$\mathrm {DP}$
? -
2. For each
 $n \geq 2$
, does there exist an
$n \geq 2$
, does there exist an
 $\mathcal {L}_A(\Box )$
-theory which has
$\mathcal {L}_A(\Box )$
-theory which has
 $\mathrm {B}^n$
-
$\mathrm {B}^n$
-
 $\mathrm {DP}$
but does not have
$\mathrm {DP}$
but does not have
 $\mathrm {B}^{n+1}$
-
$\mathrm {B}^{n+1}$
-
 $\mathrm {DP}$
?
$\mathrm {DP}$
?
For any
![]() $\Sigma _1$
-unsound r.e. extension T of
$\Sigma _1$
-unsound r.e. extension T of
![]() $\mathbf {PA}(\mathbf {Verum})$
, T has
$\mathbf {PA}(\mathbf {Verum})$
, T has
![]() $\mathrm {B}$
-
$\mathrm {B}$
-
![]() $\mathrm {DP}$
but does not have
$\mathrm {DP}$
but does not have
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {DC}$
(see Propositions 4.25 and 5.29). On the other hand, for consistent r.e. extensions of
$\mathrm {DC}$
(see Propositions 4.25 and 5.29). On the other hand, for consistent r.e. extensions of
![]() $\mathbf {PA}(\mathbf {S4})$
,
$\mathbf {PA}(\mathbf {S4})$
,
![]() $\mathrm {B}$
-
$\mathrm {B}$
-
![]() $\mathrm {DP}$
implies
$\mathrm {DP}$
implies
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {DC}$
by Propositions 4.17 and 5.39 and Corollary 5.32. We have not yet been sure whether
$\mathrm {DC}$
by Propositions 4.17 and 5.39 and Corollary 5.32. We have not yet been sure whether
![]() $\mathrm {B}$
-
$\mathrm {B}$
-
![]() $\mathrm {DP}$
yields
$\mathrm {DP}$
yields
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {DC}$
in general when
$\mathrm {DC}$
in general when
![]() $T \nvdash \Box \bot $
.
$T \nvdash \Box \bot $
.
Problem 7.68. Does there exist an
![]() $\mathcal {L}_A(\Box )$
-theory T such that
$\mathcal {L}_A(\Box )$
-theory T such that
![]() $T \nvdash \Box \bot $
, T has
$T \nvdash \Box \bot $
, T has
![]() $\mathrm {B}$
-
$\mathrm {B}$
-
![]() $\mathrm {DP}$
, and T is not
$\mathrm {DP}$
, and T is not
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {DC}$
?
$\mathrm {DC}$
?
In the statement of Proposition 5.39, it is assumed that T is an extension of
![]() $\mathbf {PA}(\mathbf {K4})$
. It is not settled yet whether
$\mathbf {PA}(\mathbf {K4})$
. It is not settled yet whether
![]() $\mathbf {PA}(\mathbf {K4})$
can be replaced by
$\mathbf {PA}(\mathbf {K4})$
can be replaced by
![]() $\mathbf {PA}(\mathbf {K})$
in the statement.
$\mathbf {PA}(\mathbf {K})$
in the statement.
Problem 7.69. In the statements of Proposition 5.39 and Corollaries 5.40 and 6.61.1, can
![]() $\mathbf {PA}(\mathbf {K4})$
be replaced by
$\mathbf {PA}(\mathbf {K4})$
be replaced by
![]() $\mathbf {PA}(\mathbf {K})$
?
$\mathbf {PA}(\mathbf {K})$
?
Proposition 6.65.1 shows that there exists an
![]() $\mathcal {L}_A(\Box )$
-unsound subtheory T of
$\mathcal {L}_A(\Box )$
-unsound subtheory T of
![]() $\mathbf {PA}(\mathbf {S4})$
. Related to this fact, we propose the following problem.
$\mathbf {PA}(\mathbf {S4})$
. Related to this fact, we propose the following problem.
Problem 7.70. Does there exist an
![]() $\mathcal {L}_A(\Box )$
-unsound r.e. subtheory of
$\mathcal {L}_A(\Box )$
-unsound r.e. subtheory of
![]() $\mathbf {PA}(\mathbf {GL})$
?
$\mathbf {PA}(\mathbf {GL})$
?
Proposition 6.66 shows that
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {DC}$
does not imply
$\mathrm {DC}$
does not imply
![]() $\mathrm {B}$
-
$\mathrm {B}$
-
![]() $\mathrm {DP}$
. We are not successful in determining whether the theory T in the proof of Proposition 6.66 is closed in the box elimination rule. We then propose the following problem.
$\mathrm {DP}$
. We are not successful in determining whether the theory T in the proof of Proposition 6.66 is closed in the box elimination rule. We then propose the following problem.
Problem 7.71. Does there exist a consistent r.e.
![]() $\mathcal {L}_A(\Box )$
-theory T such that T is closed under the box elimination rule, T is
$\mathcal {L}_A(\Box )$
-theory T such that T is closed under the box elimination rule, T is
![]() $\Sigma (\mathrm {B})$
-
$\Sigma (\mathrm {B})$
-
![]() $\mathrm {DC}$
, and T does not have
$\mathrm {DC}$
, and T does not have
![]() $\mathrm {MDP}$
?
$\mathrm {MDP}$
?
Remark 7.72. Notice that if we define T to be the theory
![]() $\mathbf {PA}(\mathbf {K4}) + \{\Box \varphi \lor \Box \neg \varphi \}$
for a
$\mathbf {PA}(\mathbf {K4}) + \{\Box \varphi \lor \Box \neg \varphi \}$
for a
![]() $\Pi _1$
Gödel sentence
$\Pi _1$
Gödel sentence
![]() $\varphi $
of
$\varphi $
of
![]() $\mathbf {PA}(\mathbf {K4})$
, then T is not closed under the box elimination rule. This is because
$\mathbf {PA}(\mathbf {K4})$
, then T is not closed under the box elimination rule. This is because
![]() $T \vdash \Box (\Box \varphi \lor \neg \varphi )$
and
$T \vdash \Box (\Box \varphi \lor \neg \varphi )$
and
![]() $T \nvdash \Box \varphi \lor \neg \varphi $
. For, if
$T \nvdash \Box \varphi \lor \neg \varphi $
. For, if
![]() $T \vdash \Box \varphi \lor \neg \varphi $
, then
$T \vdash \Box \varphi \lor \neg \varphi $
, then
![]() $\mathbf {PA}(\mathbf {K4}) \vdash \Box \neg \varphi \to (\Box \varphi \lor \neg \varphi )$
. By Proposition 6.46,
$\mathbf {PA}(\mathbf {K4}) \vdash \Box \neg \varphi \to (\Box \varphi \lor \neg \varphi )$
. By Proposition 6.46,
![]() $\mathbf {PA} \vdash \mathrm {Pr}_{\mathbf {PA}(\mathbf {K4})}(\ulcorner \neg \varphi \urcorner ) \to (\mathrm {Pr}_{\mathbf {PA}(\mathbf {K4})}(\ulcorner \varphi \urcorner ) \lor \neg \varphi )$
. Since
$\mathbf {PA} \vdash \mathrm {Pr}_{\mathbf {PA}(\mathbf {K4})}(\ulcorner \neg \varphi \urcorner ) \to (\mathrm {Pr}_{\mathbf {PA}(\mathbf {K4})}(\ulcorner \varphi \urcorner ) \lor \neg \varphi )$
. Since
![]() $\mathrm {Pr}_{\mathbf {PA}(\mathbf {K4})}(\ulcorner \varphi \urcorner )$
is
$\mathrm {Pr}_{\mathbf {PA}(\mathbf {K4})}(\ulcorner \varphi \urcorner )$
is
![]() $\mathbf {PA}(\mathbf {K4})$
-equivalent to
$\mathbf {PA}(\mathbf {K4})$
-equivalent to
![]() $\neg \varphi $
, we have
$\neg \varphi $
, we have
![]() $\mathbf {PA}(\mathbf {K4}) \vdash \mathrm {Pr}_{\mathbf {PA}(\mathbf {K4})}(\ulcorner \neg \varphi \urcorner ) \to \neg \varphi $
. By Löb’s theorem,
$\mathbf {PA}(\mathbf {K4}) \vdash \mathrm {Pr}_{\mathbf {PA}(\mathbf {K4})}(\ulcorner \neg \varphi \urcorner ) \to \neg \varphi $
. By Löb’s theorem,
![]() $\mathbf {PA}(\mathbf {K4}) \vdash \neg \varphi $
. This contradicts the
$\mathbf {PA}(\mathbf {K4}) \vdash \neg \varphi $
. This contradicts the
![]() $\Sigma _1$
-soundness of
$\Sigma _1$
-soundness of
![]() $\mathbf {PA}(\mathbf {K4})$
.
$\mathbf {PA}(\mathbf {K4})$
.
Acknowledgments
The authors would like to thank the anonymous referees for their valuable comments and suggestions on earlier versions of this paper. This work was partly supported by JSPS KAKENHI Grant Number JP19K14586.