Article contents
DEPENDENT CHOICE, PROPERNESS, AND GENERIC ABSOLUTENESS
Published online by Cambridge University Press: 02 July 2020
Abstract
We show that Dependent Choice is a sufficient choice principle for developing the basic theory of proper forcing, and for deriving generic absoluteness for the Chang model in the presence of large cardinals, even with respect to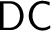 $\mathsf {DC}$
-preserving symmetric submodels of forcing extensions. Hence,
$\mathsf {DC}$
-preserving symmetric submodels of forcing extensions. Hence,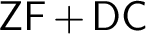 $\mathsf {ZF}+\mathsf {DC}$
not only provides the right framework for developing classical analysis, but is also the right base theory over which to safeguard truth in analysis from the independence phenomenon in the presence of large cardinals. We also investigate some basic consequences of the Proper Forcing Axiom in
$\mathsf {ZF}+\mathsf {DC}$
not only provides the right framework for developing classical analysis, but is also the right base theory over which to safeguard truth in analysis from the independence phenomenon in the presence of large cardinals. We also investigate some basic consequences of the Proper Forcing Axiom in $\mathsf {ZF}$
, and formulate a natural question about the generic absoluteness of the Proper Forcing Axiom in
$\mathsf {ZF}$
, and formulate a natural question about the generic absoluteness of the Proper Forcing Axiom in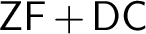 $\mathsf {ZF}+\mathsf {DC}$
and
$\mathsf {ZF}+\mathsf {DC}$
and $\mathsf {ZFC}$
. Our results confirm
$\mathsf {ZFC}$
. Our results confirm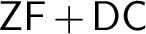 $\mathsf {ZF} + \mathsf {DC}$
as a natural foundation for a significant portion of “classical mathematics” and provide support to the idea of this theory being also a natural foundation for a large part of set theory.
$\mathsf {ZF} + \mathsf {DC}$
as a natural foundation for a significant portion of “classical mathematics” and provide support to the idea of this theory being also a natural foundation for a large part of set theory.
- Type
- Research Article
- Information
- Copyright
- © Association for Symbolic Logic, 2020
References
BIBLIOGRAPHY
- 3
- Cited by



