Article contents
BELIEF REVISION IN NON-CLASSICAL LOGICS
Published online by Cambridge University Press: 01 October 2008
Abstract
In this article, we propose a belief revision approach for families of (non-classical) logics whose semantics are first-order axiomatisable. Given any such (non-classical) logic 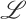 , the approach enables the definition of belief revision operators for
, the approach enables the definition of belief revision operators for 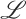 , in terms of a belief revision operation satisfying the postulates for revision theory proposed by Alchourrón, Gärdenfors and Makinson (AGM revision, Alchourrón et al. (1985)). The approach is illustrated by considering the modal logic K, Belnap's four-valued logic, and Łukasiewicz's many-valued logic. In addition, we present a general methodology to translate algebraic logics into classical logic. For the examples provided, we analyse in what circumstances the properties of the AGM revision are preserved and discuss the advantages of the approach from both theoretical and practical viewpoints.
, in terms of a belief revision operation satisfying the postulates for revision theory proposed by Alchourrón, Gärdenfors and Makinson (AGM revision, Alchourrón et al. (1985)). The approach is illustrated by considering the modal logic K, Belnap's four-valued logic, and Łukasiewicz's many-valued logic. In addition, we present a general methodology to translate algebraic logics into classical logic. For the examples provided, we analyse in what circumstances the properties of the AGM revision are preserved and discuss the advantages of the approach from both theoretical and practical viewpoints.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2008
References
BIBLIOGRAPHY
- 12
- Cited by


