This paper studies the computational complexity of the properinterval colored graph problem (PICG), when the input graphis a colored caterpillar, parameterized by hair length. In order prove ourresult we establish a close relationship between the PICG anda graph layout problem the proper colored layout problem(PCLP). We show a dichotomy: the PICG and thePCLP are NP-complete for colored caterpillars of hair length ≥2, while both problems are in P for colored caterpillarsof hair length <2.For the hardness results we provide a reduction from the multiprocessor scheduling problem, while the polynomial time resultsfollow from a characterization in terms of forbidden subgraphs.

We study infinite words u over an alphabet $\mathcal{A}$ satisfying the property $\mathcal{P} :~\mathcal{P}(n)+\mathcal{P}(n+1) = 1+ \#\mathcal{A}\ {\rm for\ any}\ n \in\mathbb{N}$ , where $\mathcal{P}(n)$ denotes the number ofpalindromic factors of length n occurring in the language of u.We study also infinite words satisfying a strongerproperty $\mathcal{PE}$ : every palindrome of u has exactly one palindromic extension in u. For binary words, the properties $\mathcal{P}$ and $\mathcal{PE}$ coincide and these properties characterize Sturmian words, i.e.,words with the complexity C(n) = n + 1 for any $n \in \mathbb{N}$ . In this paper, we focus on ternary infinite wordswith the language closed under reversal. For such words u,we prove that if C(n) = 2n + 1 for any $n \in \mathbb{N}$ ,then u satisfies the property $\mathcal{P}$ andmoreover u is rich in palindromes. Also a sufficient condition for the property $\mathcal{PE}$ is given.We construct a word demonstrating that $\mathcal{P}$ on a ternaryalphabet does not imply $\mathcal{PE}$ .

This paper presents two extensions of the second order polymorphiclambda calculus, system F, with monotone (co)inductive types supporting(co)iteration, primitive (co)recursion and inversion principles asprimitives. One extension is inspired by the usual categoricalapproach to programming by means of initial algebras and finalcoalgebras; whereas the other models dialgebras, and can be seen as an extension of Hagino'scategorical lambda calculus within the framework of parametricpolymorphism. The systems are presented in Curry-style, and are proven to be terminating andtype-preserving. Moreovertheir expressiveness is shown by means of several programmingexamples, going from usual data types to lazy codata types such as streamsor infinite trees.

A well known result of Fraenkel and Simpson states that the number of distinct squares in a word of length n is bounded by 2n since at each position there are at most two distinct squares whose last occurrence starts. In this paper, we investigate squares in partial words with one hole,or sequences over a finite alphabet that have a “do not know” symbol or “hole”. A square in a partial word over a given alphabet has the form uv where u is compatible with v, and consequently, such square is compatible with a number of words over the alphabet that are squares. Recently, it was shown that for partial words with one hole, there may be more than two squares that have their last occurrence starting at the same position. Here, we prove that if such is the case, then the length of the shortest square is at most half the length of the third shortest square.As a result, we show that the number of distinct squares compatible with factors of a partial word with one hole of length n is bounded by $\frac{7n}{2}$ .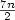

We show that Dejean's conjectureholds for n ≥ 27. This brings the final resolution of the conjecture by the approach of Moulin Ollagnier within range of the computationally feasible.

We describe a technique that maps unranked trees to arbitrary hash codes using a bottom-up deterministic tree automaton (DTA). In contrast to other hashing techniques based on automata, our procedure builds a pseudo-minimal DTA for this purpose. A pseudo-minimal automaton may be larger than the minimal one accepting the same language but, in turn, it contains proper elements (states or transitions which are unique) for every input accepted by the automaton. Therefore, pseudo-minimal DTA are a suitable structure to implement stable hashing schemes, that is, schemes where the output for every key can be determined prior to the automaton construction. We provide incremental procedures to build the pseudo-minimal DTA and the mapping that associates an integer value to every transition that will be used to compute the hash codes. This incremental construction allows for the incorporation of new trees and their hash codes without the need to rebuild the whole DTA from scratch.