Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T09:26:42.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Well quasi-orders, unavoidable sets, and derivation systems

Published online by Cambridge University Press:  18 October 2006

Flavio D'Alessandro  and
Stefano Varricchio
Flavio D'Alessandro
Affiliation:
Dipartimento di Matematica, Università di Roma “La Sapienza” Piazzale Aldo Moro 2, 00185 Roma, Italy; [email protected]
Stefano Varricchio
Affiliation:
Dipartimento di Matematica, Università di Roma “Tor Vergata”, via della Ricerca Scientifica, 00133 Roma, Italy; [email protected]
Get access

Abstract

Let I be a finite set of words and $\Rightarrow_I^*$ be the derivation relation generated by the set of productions {ε → u | u ∈ I}. Let $L_I^{\epsilon}$ be the set of words u such that $\epsilon \Rightarrow_I^* u$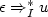. We prove that the set I is unavoidable if and only if the relation $\Rightarrow_I^*$ is a well quasi-order on the set $L_I^{\epsilon}$. This result generalizes a theorem of [Ehrenfeucht et al.,Theor. Comput. Sci.27 (1983) 311–332]. Further generalizations are investigated.

Keywords

Well quasi-orderscontext-free languages.
Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 40 , Issue 3: Word Avoidability Complexity And Morphisms (WACAM) , July 2006 , pp. 407 - 426
Copyright
© EDP Sciences, 2006

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bovet, D.P. and Varricchio, S., On the regularity of languages on a binary alphabet generated by copying systems. Inform. Process. Lett. 44 (1992) 119–123. CrossRef
D'Alessandro, F. and Varricchio, S., On well quasi-orders on languages. Lect. Notes Comput. Sci. 2710 (2003) 230–241, CrossRef
D'Alessandro, F. and Varricchio, S., Well quasi-orders and context-free grammars. Theor. Comput. Sci. 327 (2004) 255–268. CrossRef
de Luca, A. and Varricchio, S., Some regularity conditions based on well quasi-orders. Lect. Notes Comput. Sci. 583 (1992) 356–371. CrossRef
de Luca, A. and Varricchio, S., Well quasi-orders and regular languages. Acta Inform. 31 (1994) 539–557. CrossRef
A. de Luca and S. Varricchio, Finiteness and regularity in semigroups and formal languages. EATCS Monographs on Theoretical Computer Science, Springer, Berlin (1999).
Ehrenfeucht, A., Haussler, D. and Rozenberg, G., On regularity of context-free languages. Theor. Comput. Sci. 27 (1983) 311–332. CrossRef
Harju, T. and Ilie, L., On well quasi orders of words and the confluence property. Theor. Comput. Sci. 200 (1998) 205–224. CrossRef
Haussler, D., Another generalization of Higman's well quasi-order result on ∑*. Discrete Math. 57 (1985) 237–243. CrossRef
Higman, G.H., Ordering by divisibility in abstract algebras. Proc. London Math. Soc. 3 (1952) 326–336. CrossRef
Ilie, L. and Salomaa, A., On well quasi orders of free monoids. Theor. Comput. Sci. 204 (1998) 131–152. CrossRef
Intrigila, B. and Varricchio, S., On the generalization of Higman and Kruskal's theorems to regular languages and rational trees. Acta Inform. 36 (2000) 817–835. CrossRef
Ito, M., Kari, L. and Thierrin, G., Shuffle and scattered deletion closure of languages. Theor. Comput. Sci. 245 (2000) 115–133. CrossRef
Jantzen, M., Extending regular expressions with iterated shuffle. Theor. Comput. Sci. 38 (1985) 223–247. CrossRef
Kruskal, J., The theory of well quasi-ordering: a frequently discovered concept. J. Combin. Theory Ser. A 13 (1972) 297–305. CrossRef
Puel, L., Using unavoidable sets of trees to generalize Kruskal's theorem. J. Symbolic Comput. 8 (1989) 335–382. CrossRef