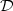Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rothe, Jan
2002.
A Syntactical Approach to Weak (Bi-)Simulation for Coalgebras.
Electronic Notes in Theoretical Computer Science,
Vol. 65,
Issue. 1,
p.
270.
Rothe, Jan
and
Mašulović, Dragan
2002.
Towards Weak Bisimulation For Coalgebras.
Electronic Notes in Theoretical Computer Science,
Vol. 68,
Issue. 1,
p.
32.
Chen, Hubie
and
Pucella, Riccardo
2003.
A Coalgebraic Approach to Kleene Algebra with Tests.
Electronic Notes in Theoretical Computer Science,
Vol. 82,
Issue. 1,
p.
94.
Chen, Hubie
and
Pucella, Riccardo
2004.
A coalgebraic approach to Kleene algebra with tests.
Theoretical Computer Science,
Vol. 327,
Issue. 1-2,
p.
23.
Sokolova, Ana
de Vink, Erik
and
Woracek, Harald
2005.
Weak Bisimulation for Action-Type Coalgebras.
Electronic Notes in Theoretical Computer Science,
Vol. 122,
Issue. ,
p.
211.
Thiyagarajan, M.
and
Sairam, N.
2007.
Verification of the correctness of compiler optimization using co-induction.
Journal of Discrete Mathematical Sciences and Cryptography,
Vol. 10,
Issue. 3,
p.
329.
Nakata, Keiko
and
Uustalu, Tarmo
2009.
Theorem Proving in Higher Order Logics.
Vol. 5674,
Issue. ,
p.
375.
Nakata, Keiko
and
Uustalu, Tarmo
2010.
Programming Languages and Systems.
Vol. 6012,
Issue. ,
p.
488.
Gribovskaya, Natalya
and
Virbitskaite, Irina
2010.
Theory and Applications of Models of Computation.
Vol. 6108,
Issue. ,
p.
443.
Nakata, Keiko
2011.
Resumption-based big-step and small-step interpreters for While with interactive I/O.
Electronic Proceedings in Theoretical Computer Science,
Vol. 66,
Issue. ,
p.
226.
Danielsson, Nils Anders
2012.
Operational semantics using the partiality monad.
p.
127.
Danielsson, Nils Anders
2012.
Operational semantics using the partiality monad.
ACM SIGPLAN Notices,
Vol. 47,
Issue. 9,
p.
127.
Brengos, Tomasz
2012.
Theoretical Computer Science.
Vol. 7604,
Issue. ,
p.
87.
Piróg, Maciej
and
Gibbons, Jeremy
2013.
Monads for Behaviour.
Electronic Notes in Theoretical Computer Science,
Vol. 298,
Issue. ,
p.
309.
Brengos, Tomasz
2014.
Advanced Information Systems Engineering.
Vol. 7908,
Issue. ,
p.
75.
Goncharov, Sergey
Rauch, Christoph
and
Schröder, Lutz
2015.
Unguarded Recursion on Coinductive Resumptions.
Electronic Notes in Theoretical Computer Science,
Vol. 319,
Issue. ,
p.
183.
Tsampas, Stelios
Nuyts, Andreas
Devriese, Dominique
and
Piessens, Frank
2020.
Coalgebraic Methods in Computer Science.
Vol. 12094,
Issue. ,
p.
155.