Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T04:33:09.206Z Has data issue: false hasContentIssue false
  • English
  • Français

Function operators spanning the arithmetical and the polynomial hierarchy

Published online by Cambridge University Press:  05 October 2010

Armin Hemmerling
Armin Hemmerling*
Affiliation:
Ernst-Moritz-Arndt–Universität Greifswald, Institut für Mathematik und Informatik. Walther-Rathenau-Str. 47, 17487 Greifswald, Germany; [email protected]
Get access

Abstract

A modified version of the classical µ-operator as well as the first value operator and the operator of inverting unary functions, applied in combination with the composition of functions and starting from the primitive recursive functions, generate all arithmetically representable functions. Moreover, the nesting levels of these operators are closely related to the stratification of the arithmetical hierarchy. The same is shown for some further function operators known from computability and complexity theory. The close relationships between nesting levels of operators and the stratification of the hierarchy also hold for suitable restrictions of the operators with respect to the polynomial hierarchy if one starts with the polynomial-time computable functions. It follows that questions around P vs. NP and NP vs. coNP can equivalently be expressed by closure properties of function classes under these operators. The polytime version of the first value operator can be used to establish hierarchies between certain consecutive levels within the polynomial hierarchy of functions, which are related to generalizations of the Boolean hierarchies over the classes $\mbox{$\Sigma^p_{k}$}$.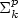

Keywords

Arithmetical hierarchypolynomial hierarchyBoolean hierarchyP versus NPNP versus coNPfirst value operatorminimalizationinversion of functions
Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 44 , Issue 3 , July 2010 , pp. 379 - 418
Copyright
© EDP Sciences, 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Buss, S. and On, L. Hay truth-table reducibility to SAT. Inf. Comput. 91 (1991) 86–102. CrossRef
J.L. Balcazar, J. Diaz and J. Gabarro, Structural complexity I and II. Springer-Verlag, Berlin (1990).
Bellantoni, S.J. and Niggl, K.-H., Ranking primitive recursions: the low Grzegorczyk classes revised. SIAM Journal on Computing 29 (1999) 401–415. CrossRef
Cai, J.-Y., Gundermann, T., Hartmanis, J., Hemachandra, L., Sawelson, V., Wagner, K. and Wechsung, G., The Boolean hierarchy I: structural properties. SIAM Journal on Computing 17 (1988) 1232–1252. CrossRef
Cai, J.-Y., Gundermann, T., Hartmanis, J., Hemachandra, L., Sawelson, V., Wagner, K. and Wechsung, G., The Boolean hierarchy II: applications. SIAM Journal on Computing 18 (1989) 95–111. CrossRef
S.B. Cooper, Computability theory. Chapman & Hall/CRC, Boca Raton (2004).
D.-Z. Du and K.-I. Ko, Theory of computational complexity. Wiley-Interscience, New York (2000).
R.L. Epstein, R. Haas and R.L. Kramer, Hierarchies of sets and degrees below 0'. In: Logic Year (1979/80), Univ. of Connecticut, edited by M. Lerman, J.H. Schmerl, R.I. Soare. LN in Math 859. Springer Verlag, 32–48.
Y.L. Ershov, A hierarchy of sets. I; II; III. Algebra i Logica 7 (1968) no. 1, 47–74; no. 4, 15–47; 9 (1970), no. 1, 34–51 (English translation by Plenum P.C.).
M.R. Garey and D.S. Johnson, Computers and intractability – a guide to the theory of NP–completeness. W.H. Freeman, San Francisco (1979).
F. Hausdorff, Grundzüge der Mengenlehre. W. de Gruyter & Co., Berlin and Leipzig (1914); Reprint: Chelsea P.C., New York (1949).
Hemmerling, A., The Hausdorff-Ershov hierarchy in Euclidean spaces. Arch. Math. Logic 45 (2006) 323–350. CrossRef
Hemmerling, A., Hierarchies of function classes defined by the first-value operator. RAIRO - Theor. Inf. Appl. 42 (2008) 253–270. Extended abstract in: Proc. of CCA'2004. Electronic Notes in Theoretical Computer Science 120 (2005) 59–72. CrossRef
J. Krajicek, Bounded arithmetic, propositional logic, and complexity theory. Cambridge Univ. Press (1995).
Krentel, M.W., The complexity of optimization problems. J. Comput. Syst. Sci. 36 (1988) 490–509. CrossRef
A.I. Malcev, Algorithmen und rekursive Funktionen. Akademie-Verlag, Berlin (1974).
P. Odifreddi, Classical recursion theory. North-Holland P.C., Amsterdam (1989).
C.H. Papadimitriou, Computational complexity. Addison Wesley P.C., Reading (1994).
C. Parsons, Hierarchies of primitive recursive functions. Zeitschr. f. Math. Logik u. Grundl. d. Math. 14 (1968) 357–376. CrossRef
Robinson, J., General recursive functions. Proc. Am. Math. Soc. 72 (1950) 703–718. CrossRef
H. Rogers Jr, Theory of recursive functions and effective computability. McGraw-Hill, New York (1967).
H.E. Rose, Subrecursion: functions and hierarchies. Clarendon Press, Oxford (1984).
J. Rothe, Complexity theory and cryptology. Springer-Verlag, Berlin (2005).
Schwichtenberg, H., Rekursionszahlen und Grzegorczyk-Hierarchie. Arch. Math. Logic 12 (1969) 85–97. CrossRef
Selman, A.L., A survey of one-way functions in complexity theory. Math. Syst. Theory 25 (1992) 203–221. CrossRef
Selman, A., A taxonomy of complexity classes of functions. J. Comput. Syst. Sci. 48 (1994) 357–381. CrossRef
Shoenfield, J.R., On degrees of unsolvability. Ann. Math. 69 (1959) 644–653. CrossRef
R.I. Soare, Recursively enumerable sets and degrees. Springer-Verlag, Berlin (1987).
Soare, R.I., Computability and recursion. Bulletin of symbolic Logic 2 (1996) 284–321. CrossRef
R.I. Soare, Computability theory and applications. Springer-Verlag, Berlin, forthcoming.
Wagner, K.W., Bounded query classes. SIAM Journal on Computing 19 (1990) 833–846. CrossRef
G. Wechsung, Vorlesungen zur Komplexitätstheorie. B.G. Teubner, Stuttgart (2000).
K. Weihrauch, Computability. Springer-Verlag, Berlin (1987).