Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T17:01:32.721Z Has data issue: false hasContentIssue false
  • English
  • Français

The Fibonacci automorphismof free Burnside groups

Published online by Cambridge University Press:  26 August 2011

Ashot S. Pahlevanyan
Ashot S. Pahlevanyan*
Affiliation:
Faculty of Mathematics and Mechanics, Yerevan State University, A. Manoogian st. 1, Yerevan-0025, Armenia. [email protected]
Get access

Abstract

We prove that the Fibonacci morphism is an automorphism of infinite order of free Burnside groups for all odd $n\geq 665$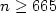 and even $n = 16k \geq 8000$.

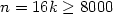Keywords

Free periodic groupsBurnside groupsgroupautomorphismsFibonacci morphismFibonacci sequenceFibonacciwordgolden ratio
Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 45 , Issue 3 , July 2011 , pp. 301 - 309
Copyright
© EDP Sciences, 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

S.I. Adian, The Burnside Problem and Identities in Groups. Nauka (1975); English translation, Springer-Verlag (1979) 1–336.
Atabekyan, V.S., Non-$\varphi$-admissible normal subgroups of free Burnside groups. J. Contemp. Math. Anal. 45 (2010) 112–122. CrossRef
Atabekyan, V.S., Normal automorphisms of free Burnside groups. Izv. RAN. Ser. Math. 75 (2011) 3–18. CrossRef
Cherepanov, E.A., Free semigroup in the group of automorphisms of the free Burnside group. Comm. Algebra 33 (2005) 539–547. CrossRef
Cherepanov, E.A., Normal automorphisms of free Burnside groups of large odd exponents. Int. J. Algebra Comput. 16 (2006) 839–847. CrossRef
Karhumäki, J., On cube-free $\omega$-words generated by binary morphisms. Disc. Appl. Math. 5 (1983) 279–297. CrossRef
Kourovka Notebook, Unsolved Problems in Group Theory. Novosibirsk (2006).
Lysënok, I.G., Infinite Burnside groups of even exponent. Izv. Math. 60 (1996) 453–654. CrossRef
Mignosi, F. and Pirillo, G., Repetitions in the Fibonacci infinite word. Informatique Théorique et Applications 26 (1992) 199–204. CrossRef