Published online by Cambridge University Press: 15 April 2002
We present an algorithm for computing the prefix of an automaton.
Automata considered are non-deterministic, labelled on words, and can
have ε-transitions. The prefix automaton of an automaton
$\mathcal{A}$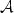 has the following characteristic properties. It has the
same graph as $\mathcal{A}$
has the following characteristic properties. It has the
same graph as $\mathcal{A}$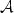 . Each accepting path has the same label as in
$\mathcal{A}$
. Each accepting path has the same label as in
$\mathcal{A}$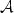 . For each state q, the longest common prefix of the
labels of all paths going from q to an initial or final state is empty.
The interest of the computation of the prefix of an automaton is that it
is the first step of the minimization of sequential transducers.
The algorithm that we describe has the same worst case time complexity as
another algorithm due to Mohri but our algorithm allows automata that
have empty labelled cycles. If we denote by P(q) the longest common
prefix of labels of paths going from q to an initial or final state, it
operates in time O((P+1) × |E|) where P is the maximal length of
all P(q).
. For each state q, the longest common prefix of the
labels of all paths going from q to an initial or final state is empty.
The interest of the computation of the prefix of an automaton is that it
is the first step of the minimization of sequential transducers.
The algorithm that we describe has the same worst case time complexity as
another algorithm due to Mohri but our algorithm allows automata that
have empty labelled cycles. If we denote by P(q) the longest common
prefix of labels of paths going from q to an initial or final state, it
operates in time O((P+1) × |E|) where P is the maximal length of
all P(q).