Article contents
Coalgebras for Binary Methods: Properties of Bisimulations and Invariants
Published online by Cambridge University Press: 15 April 2002
Abstract
Coalgebras for endofunctors ${\mathcal C}\rightarrow{\mathcal
C}$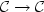 can be used to model classes of object-oriented
languages. However, binary methods do not fit directly into
this approach. This paper proposes an extension of the
coalgebraic framework, namely the use of extended
polynomial functors${\mathcal C}^{op} \times {\mathcal
C}\rightarrow{\mathcal C}$
can be used to model classes of object-oriented
languages. However, binary methods do not fit directly into
this approach. This paper proposes an extension of the
coalgebraic framework, namely the use of extended
polynomial functors${\mathcal C}^{op} \times {\mathcal
C}\rightarrow{\mathcal C}$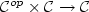 . This extension allows the incorporation
of binary methods into coalgebraic class specifications. The
paper also discusses how to define bisimulation and invariants
for coalgebras
of extended polynomial functors and proves many standard
results.
. This extension allows the incorporation
of binary methods into coalgebraic class specifications. The
paper also discusses how to define bisimulation and invariants
for coalgebras
of extended polynomial functors and proves many standard
results.
- Type
- Research Article
- Information
- RAIRO - Theoretical Informatics and Applications , Volume 35 , Issue 1: Coalgebraic Methods in Computer Science , January 2001 , pp. 83 - 111
- Copyright
- © EDP Sciences, 2001
References
- 3
- Cited by


