Article contents
Arithmetization of the field of reals with exponentiation extended abstract
Published online by Cambridge University Press: 18 January 2008
Abstract
(1) Shepherdson proved that a discrete unitary commutative semi-ring
A+ satisfies IE0 (induction scheme restricted to quantifier
free formulas) iff A is integral part of a
real closed field; and Berarducci asked about extensions of this
criterion when exponentiation is added to the language of rings. Let T range over axiom systems for ordered fields with
exponentiation; for three values of T we provide a theory
$_{\llcorner} T _{\lrcorner}$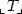 in the language of rings plus exponentiation such that the
models (A, expA) of $_{\llcorner} T _{\lrcorner}$
in the language of rings plus exponentiation such that the
models (A, expA) of $_{\llcorner} T _{\lrcorner}$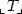 are all integral parts A of models
M of T with A+ closed under expM and
expA = expM | A+. Namely T = EXP, the basic theory of
real exponential fields; T = EXP+ the Rolle and the intermediate
value properties for all 2x-polynomials; and T = Texp, the
complete theory of the field of reals with exponentiation.
(2)$_{\llcorner}$
are all integral parts A of models
M of T with A+ closed under expM and
expA = expM | A+. Namely T = EXP, the basic theory of
real exponential fields; T = EXP+ the Rolle and the intermediate
value properties for all 2x-polynomials; and T = Texp, the
complete theory of the field of reals with exponentiation.
(2)$_{\llcorner}$ Texp$_{\lrcorner}$
Texp$_{\lrcorner}$ is recursively axiomatizable iff Texp is
decidable. $_{\llcorner}$
is recursively axiomatizable iff Texp is
decidable. $_{\llcorner}$ Texp$_{\lrcorner}$
Texp$_{\lrcorner}$ implies LE0(xy) (least element
principle for open formulas in the language <,+,x,-1,xy)
but the reciprocal is an open question. $_{\llcorner}$
implies LE0(xy) (least element
principle for open formulas in the language <,+,x,-1,xy)
but the reciprocal is an open question. $_{\llcorner}$ Texp$_{\lrcorner}$
Texp$_{\lrcorner}$ satisfies
“provable polytime witnessing”: if $_{\llcorner} $
satisfies
“provable polytime witnessing”: if $_{\llcorner} $ Texp$_{\lrcorner}$
Texp$_{\lrcorner}$ proves ∀x∃y : |y| < |x|k)R(x,y) (where $|y|:=_{\llcorner}$
proves ∀x∃y : |y| < |x|k)R(x,y) (where $|y|:=_{\llcorner}$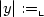 log(y)$_{\lrcorner}$
log(y)$_{\lrcorner}$ , k < ω
and R is an NP relation), then it proves ∀x R(x,ƒ(x))
for some polynomial time function f.
(3) We introduce “blunt” axioms for Arithmetics: axioms which do as
if every real number was a fraction (or even a dyadic number). The
falsity of such a contention in the standard model of the integers
does not mean inconsistency; and bluntness has both a heuristic
interest and a simplifying effect on many questions – in particular
we prove that the blunt version of $_{\llcorner} $
, k < ω
and R is an NP relation), then it proves ∀x R(x,ƒ(x))
for some polynomial time function f.
(3) We introduce “blunt” axioms for Arithmetics: axioms which do as
if every real number was a fraction (or even a dyadic number). The
falsity of such a contention in the standard model of the integers
does not mean inconsistency; and bluntness has both a heuristic
interest and a simplifying effect on many questions – in particular
we prove that the blunt version of $_{\llcorner} $ Texp$_{\lrcorner}$
Texp$_{\lrcorner}$ is a
conservative extension of $_{\llcorner} $
is a
conservative extension of $_{\llcorner} $ Texp$_{\lrcorner}$
Texp$_{\lrcorner}$ for sentences in
∀Δ0(xy) (universal quantifications of bounded
formulas in the language of rings plus xy). Blunt Arithmetics –
which can be extended to a much richer language – could become a
useful tool in the non standard approach to discrete geometry, to
modelization and to approximate computation with reals.
for sentences in
∀Δ0(xy) (universal quantifications of bounded
formulas in the language of rings plus xy). Blunt Arithmetics –
which can be extended to a much richer language – could become a
useful tool in the non standard approach to discrete geometry, to
modelization and to approximate computation with reals.
- Type
- Research Article
- Information
- Copyright
- © EDP Sciences, 2007
References
- 2
- Cited by


