Article contents
Translation from classical two-way automata to pebble two-way automata
Published online by Cambridge University Press: 28 February 2011
Abstract
We study the relation between the standard two-way automata and
more powerful devices, namely, two-way finite automata equipped
with some $\ell$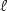 additional “pebbles” that are movable along
the input tape, but their use is restricted (nested) in
a stack-like fashion. Similarly as in the case of the classical
two-way machines, it is not known whether there exists
a polynomial trade-off, in the number of states, between the
nondeterministic and deterministic two-way automata with $\ell$
additional “pebbles” that are movable along
the input tape, but their use is restricted (nested) in
a stack-like fashion. Similarly as in the case of the classical
two-way machines, it is not known whether there exists
a polynomial trade-off, in the number of states, between the
nondeterministic and deterministic two-way automata with $\ell$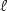 nested pebbles. However, we show that these two machine models
are not independent: if there exists a polynomial trade-off for
the classical two-way automata, then, for each $\ell$
nested pebbles. However, we show that these two machine models
are not independent: if there exists a polynomial trade-off for
the classical two-way automata, then, for each $\ell$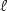 ≥ 0,
there must also exist a polynomial trade-off for the two-way
automata with $\ell$
≥ 0,
there must also exist a polynomial trade-off for the two-way
automata with $\ell$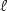 nested pebbles. Thus, we have an upward
collapse (or a downward separation) from the classical two-way
automata to more powerful pebble automata, still staying within
the class of regular languages. The same upward collapse holds
for complementation of nondeterministic two-way machines. These results are obtained by
showing that each pebble machine
can be, by using suitable inputs, simulated by a classical
two-way automaton (and vice versa), with only a linear number of
states, despite the existing exponential blow-up between the
classical and pebble two-way machines.
nested pebbles. Thus, we have an upward
collapse (or a downward separation) from the classical two-way
automata to more powerful pebble automata, still staying within
the class of regular languages. The same upward collapse holds
for complementation of nondeterministic two-way machines. These results are obtained by
showing that each pebble machine
can be, by using suitable inputs, simulated by a classical
two-way automaton (and vice versa), with only a linear number of
states, despite the existing exponential blow-up between the
classical and pebble two-way machines.
- Type
- Research Article
- Information
- RAIRO - Theoretical Informatics and Applications , Volume 44 , Issue 4 , October 2010 , pp. 507 - 523
- Copyright
- © EDP Sciences, 2011
References
- 4
- Cited by


