Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-03T05:41:35.329Z Has data issue: false hasContentIssue false
  • English
  • Français

Hierarchies of function classes defined by the first-value operator

Published online by Cambridge University Press:  25 December 2007

Armin Hemmerling
Armin Hemmerling*
Affiliation:
Ernst-Moritz-Arndt–Universität Greifswald, Institut für Mathematik und Informatik, Friedrich-Ludwig-Jahn–Str. 15a, 17487 Greifswald, Germany; [email protected]
Get access

Abstract

The first-value operator assigns to any sequence of partial functions of the same type a new such function. Its domain is the union of the domains of the sequence functions, and its value at any point is just the value of the first function in the sequence which is defined at that point. In this paper, the first-value operator is applied to establish hierarchies of classes of functions under various settings. For effective sequences of computable discrete functions, we obtain a hierarchy connected with Ershov's one within $\Delta^{0}_2$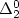. The non-effective version over real functions is connected with the degrees of discontinuity and yields a hierarchy related to Hausdorff's difference hierarchy in the Borel class $\Delta^{B}_2$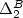. Finally, the effective version over approximately computable real functions forms a hierarchy which provides a useful tool in computable analysis.

Keywords

Hierarchies of functionsdegree of discontinuitycomputable analysiseffective descriptive set theoryHausdorff hierarchyErshov hierarchy
Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 42 , Issue 2 , April 2008 , pp. 253 - 270
Copyright
© EDP Sciences, 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Brattka, V., Effective Borel measurability and reducibility of functions. Math. Logic Quart. 51 (2005) 19–44. CrossRef
R. Engelking, General topology. Heldermann Verlag, Berlin (1989).
R.L. Epstein, R. Haas and R.L. Kramer, Hierarchies of sets and degrees below 0', in Logic Year 1979/80, Univ. of Connecticut, edited by M. Lerman, J.H. Schmerl and R.I. Soare. Lect. Notes Math. 859 32–48.
Yu. L. Ershov, A hierarchy of sets. I; II; III. Algebra Logica 7 (1968) 15–47. Algebra Logica 7 (1968) 47–74. Algebra Logica 9 (1970) 34–51 (English translation by Plenum P.C.).
F. Hausdorff, Grundzüge der Mengenlehre. W. de Gruyter & Co., Berlin and Leipzig (1914); Reprint: Chelsea P.C., New York (1949).
F. Hausdorff, Mengenlehre. W. de Gruyter & Co., Berlin and Leipzig (1927).
Hemmerling, A., Approximate decidability in Euclidean spaces. Math. Logic Quart. 49 (2003) 34–56. CrossRef
Hemmerling, A., Characterizations of the class $\Delta^{ta}_2$ over Euclidean spaces. Math. Logic Quart. 50 (2004) 507–519. CrossRef
Hemmerling, A., The Hausdorff-Ershov hierarchy in Euclidean spaces. Arch. Math. Logic 45 (2006) 323–350. CrossRef
P. Hertling, Unstetigkeitsgrade von Funktionen in der effektiven Analysis. Dissertation. Informatik Berichte 208-11/1996, Fern-Uni Hagen (1996).
Hertling, P., Topological complexity with continuous operations. J. Complexity 12 (1996) 315–338. CrossRef
P. Hertling and K. Weihrauch, Levels of degeneracy and exact lower complexity bounds for geometric algorithms, in Proc. of the 6th Canadian Conf. on Computational Geometry, Saskatoon (1994) 237–242.
A.S. Kechris, Classical descriptive set theory. Springer Verlag, New York (1995).
K.-I. Ko, Complexity theory of real functions. Birkhäuser, Boston (1991).
Ko, K.-I. and Friedman, H., Computational complexity of real functions. Theoret. Comput. Sci. 20 (1982) 323–352. CrossRef
Kreitz, C. and Weihrauch, K., Complexity theory on real numbers and functions. Lect. Notes. Comput. Sci. 145 (1982) 165–174. CrossRef
Y.N. Moschovakis, Descriptive set theory. North-Holland, Amsterdam (1980).
P. Odifreddi, Classical recursion theory. North–Holland, Amsterdam (1989).
H. Rogers Jr., Theory of recursive functions and effective computability. McGraw-Hill, New York (1967).
Selivanov, V.L., Wadge degrees of ω-languages of deterministic Turing machines. RAIRO-Theor. Inf. Appl. 37 (2003) 67–84. CrossRef
R.I. Soare, Recursively enumerable sets and degrees. Springer-Verlag, Berlin (1987).
K. Weihrauch, Computable analysis. Springer-Verlag, Berlin (2000).