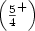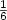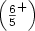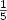Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rao, Michaël
2011.
Last cases of Dejean’s conjecture.
Theoretical Computer Science,
Vol. 412,
Issue. 27,
p.
3010.
Ochem, Pascal
Rao, Michaël
and
Rosenfeld, Matthieu
2018.
Sequences, Groups, and Number Theory.
p.
177.