Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-24T13:32:32.086Z Has data issue: false hasContentIssue false
  • English
  • Français

Communication Complexity and Lower Bounds on Multilective Computations

Published online by Cambridge University Press:  15 August 2002

Juraj Hromkovič
Juraj Hromkovič*
Affiliation:
Department of Computer Science I, Algorithms and Complexity, University of Technology, Aachen, Ahornstrasse 55, 52056 Aachen, Germany; [email protected].
Get access

Abstract

Communication complexity of two-party (multiparty)protocols has established itself as a successful method for proving lower bounds on the complexity of concrete problems for numerous computing models. While the relations between communication complexity and oblivious, semilective computations are usually transparent and the main difficulty is reduced to proving nontrivial lower bounds on the communication complexity of given computing problems, the situation essentially changes, if one considers non-oblivious or multilective computations. The known lower bound proofs for such computations are far from being transparent and the crucial ideas of these proofs are often hidden behind some nontrivial combinatorial analysis. The aim of this paper is to create a general framework for the use of two-party communication protocols for lower bound proofs on multilective computations. The result of this creation is not only a transparent presentation of some known lower bounds on the complexity of multilective computations on distinct computing models, but also the derivation of new nontrivial lower bounds on multilective VLSI circuits and multilective planar Boolean circuits.In the case of VLSI circuits we obtain a generalization ofThompson's lower bounds on AT 2 complexity for multilective circuits.The Ω(n 2) lower bound on the number of gates of any k-multilectiveplanar Boolean circuit computing a specific Boolean function of n variablesis established for $k<\frac{1}{2} \log_2 n$ 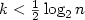. Another advantage of this framework is that it provides lower bounds for a lot of concrete functions. This contrasts to the typical papersdevoted to lower bound proofs, where one establishes a lower bound for one or a few specific functions.

Keywords

Communication complexitylower bounds on complexityBoolean functionsbranching programscircuits.
Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 33 , Issue 2 , March 1999 , pp. 193 - 212
Copyright
© EDP Sciences, 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

H. Abelson, Lower bounds on information transfer in distributed computations, in Proc. 19th IEEE FOCS, IEEE (1978) 151-158.
N. Alon and W. Maas, Meanders, Ramsey theory and lower bounds for branching programs, in Proc.27th IEEE FOCS, IEEE (1986) 410-417.
M. Ajtai, L. Babai, P. Hajnal, J. Komlós, P. Pudlák, V. Rödl, E. Szemerédi and G. Turán, Two lower bounds for branching programs, in Proc. 18th ACM STOC, ACM (1986) 30-38.
A.V. Aho, J.D. Ullman and M. Yanakakis, On notions of information transfer in VLSI circuits, in Proc. 15th ACM STOC, ACM (1983) 133-139.
Babai, L., Nisan, N. and Szegedy, M., Multiparty protocols, pseudorandom generators for logspace, and time-space trade-offs. J. Comput. System Sci. 45 (1992) 204-232. CrossRef
Borodin, A., Razborov, A. and Smolensky, R., On lower bounds for read-k-times branching programs. Computational Complexity 3 (1993) 1-18. CrossRef
Bollig, B. and Wegener, I., A very simple function that requires exponential size read-once branching programs. Inform. Process. Lett. 66 (1998) 53-57. CrossRef
Duris, P. and Galil, Z., On the power of multiple read in chip. Inform. and Comput. 104 (1993) 277-287. CrossRef
P. Duris, and Galil Z., Schnitger G., Lower bounds on communication complexity, in Proc. 16th ACM STOC, ACM (1984), 81-91.
M. Dietzfelbinger, J. Hromkovic and G. Schnitger, A comparison of two lower bounds methods for communication complexity. Theoret. Comput. Sci. 168 (1996), 39-51.
H.D. Gr÷ger, A new partition lemma for planar graphs and its application to circuit complexity, in Proc. FCT'91, Springer-Verlag, Lecture Notes in Computer Science 529 (1991) 220-229.
Hromkovic, J., Krause, M., Meinel and Ch., S. Waack, Branching programs provide lower bounds on the area of multilective deterministic and nondeterministic VLSI circuits. Inform. and Comput. 95 (1992) 117-128. CrossRef
Hromkovic, J., Nonlinear lower bounds on the number of processors of circuits with sublinear seperators. Inform. and Comput. 95 (1991) 117-128. CrossRef
J. Hromkovic, Communication Complexity and Parallel Computing. EATCS Series, Springer (1997).
Krause, M., Lower bounds for depth-restricted branching programs. Inform. and Comput. 91 (1991) 1-14. CrossRef
M. Krause, Ch. Meinel and S. Waack, Separating complexity classes related to certain input oblivious logarithmic space-bounded Turing machines, in Proc. Structure in Complexity Theory (1989) 240-249.
E. Kushilevitz and N. Nisan, Communication Complexity. Cambridge University Press (1997).
Lipton, R.J. and Tarjan, R.E., A separator theorem for planar graphs. SIAM J. Appl. Math. 36 (1979) 177-189. CrossRef
E.A. Okolnishkova, On lower bounds for branching programs. Siberian Advances in Mathematics 3 (1993) 152-166.
P. Pudlák and S. Zák, Space complexity of computation. Techn. Report, Prague (1983).
M. Sauerhoff, Lower bounds for randomized read-k-times branching programs, in Proc. STACS'98, Lecture Notes in Computer Science (1373) 105-115.
Savage, J.E., The performance of multilective VLSI algorithms. J. Comput. System Sci. 29 (1984) 243-273. CrossRef
J. Simon and M. Szegedy, A new lower bound theorem for read-only-once branching programs and its application, J. Cai, Ed., Advances in Computational Complexity Theory, DIMACS Series in Discrete Mathematics and Theoretical Computer Science 13, AMS (1993) 183-193.
P. Savický and S. Zák, A large lower bound for 1-branching programs. ECCC Report TR D36-96 (1996).
C.D. Thompson, Area-time complexity for VLSI, in Proc. 11th ACM STOC, ACM (1979) 81-88.
Gy. Turán, On restricted Boolean circuits, in Proc. FCT'89, Springer-Verlag, Lecture Notes in Computer Science 380 (1989) 460-469.
Turán, Gy., Lower bounds for synchronous circuits and planar circuits. Inform. Process. Lett. 30 (1989) 37-40. CrossRef
Gy. Turán, On the complexity of planar Boolean circuits. Comput. Complexity 5 (1995) 24-42. CrossRef
J.D. Ullman, Computational Aspects of VLSI. Comput. Science Press, Rockwille MD (1984).
I. Wegener, The Complexity of Boolean Functions. Wiley-Teubner Series in Computer Science, John Wiley and Sons Ltd., and Teubner, B.G., Stuttgart (1987).
Wegener, I., On the complexity of branching programs and decision trees for clique funcion. J. Assoc. Comput. Mach. 35 (1988) 461-471. CrossRef
A.C. Yao, Some complexity questions related to distributive computing, in Proc. 11th ACM STOC, ACM (1979) 209-213.
A.C. Yao, The entropic limitations on VLSI computations, in Proc. 11th ACM STOC, ACM (1979) 209-213.
Zák, S., An exponential lower bound for one-time-only branching programs, in Proc MFCS '84, Springer, Berlin, Lecture Notes in Computer Science 176 (1984) 562-566. CrossRef
Zák, S., An exponential lower bound for real-time branching programs. Inform. and Control 71 (1986) 87-94.