No CrossRef data available.
Article contents
Generalized Characterizationof the Convex Envelope of a Function
Published online by Cambridge University Press: 15 July 2002
Abstract
We investigate the minima of functionals of the form $$\int_{[a,b]}g(\dot u(s)){\rm d}s$$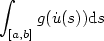 
where g is strictly convex. The admissible functions $u:[a,b]\longrightarrow\mathbb{R}$ 
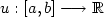are not necessarily convex and satisfy $u\leq f$ 
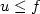on [a,b], u(a)=f(a), u(b)=f(b), f is a fixed function on [a,b].We show that the minimum is attained by $\bar f$ 
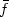, the convex envelope of f.
- Type
- Research Article
- Information
- Copyright
- © EDP Sciences, 2002
References
J. Benoist and J.B. Hiriart-Urruty, What Is the Subdifferential of the Closed Convex Hull of a Function? SIAM J. Math. Anal.
27 (1994) 1661-1679.
H. Brezis, Analyse Fonctionnelle: Théorie et Applications. Masson, Paris, France (1983).
B. Dacorogna, Introduction au Calcul des Variations. Presses Polytechniques et Universitaires Romandes, Lausanne (1992).
Kadhi, F. and Trad, A., Characterization and Approximation of the Convex Envelope of a Function.
J. Optim. Theory Appl.
110 (2001) 457-466.
CrossRef
Lachand-Robert, T. and Peletier, M.A., Minimisation de Fonctionnelles dans un Ensemble de Fonctions Convexes.
C. R. Acad. Sci. Paris Sér. I Math.
325 (1997) 851-855.
CrossRef
T. Rockafellar, Convex Analysis. Princeton University Press, Princeton, New Jersey (1970).
W. Rudin, Real and Complex Analysis, Third Edition. McGraw Hill, New York (1987).