Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-24T04:32:15.876Z Has data issue: false hasContentIssue false
  • English
  • Français

Computational schemes for two exponential servers where the first has a finite buffer

Published online by Cambridge University Press:  10 May 2011

Moshe Haviv  and
Rita Zlotnikov
Moshe Haviv
Affiliation:
Department of Statistics, The Hebrew University of Jerusalem, 91905 Jerusalem, Israel. [email protected]
Rita Zlotnikov
Affiliation:
Department of Statistics, The Hebrew University of Jerusalem, 91905 Jerusalem, Israel. [email protected]
Get access

Abstract

We consider a system consisting of two not necessarily identicalexponential servers having a common Poisson arrival process. Uponarrival, customers inspect the first queue and join it if it isshorter than some threshold n. Otherwise, they join the secondqueue. This model was dealt with, among others, by Altman et al. [Stochastic Models 20 (2004) 149–172].We first derive an explicitexpression for the Laplace-Stieltjes transform of the distributionunderlying the arrival (renewal) process to the second queue. Second,we observe that given that the second serveris busy, the two queue lengths are independent.Third, we develop two computational schemes for thestationary distribution of the two-dimensional Markov process underlying thismodel, one with a complexity of$O(n \log\delta^{-1})$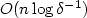, the other with a complexity of $O(\log n\log^2\delta^{-1})$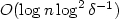, where δ is the tolerance criterion.

Keywords

Memoryless queuesquasi birth and death processesmatrix geometric
Type
Research Article
Information
RAIRO - Operations Research , Volume 45 , Issue 1 , January 2011 , pp. 17 - 36
Copyright
© EDP Sciences, ROADEF, SMAI, 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Altman, E., Jimenez, T., Nunez Queija, R. and Yechiali, U., Optimal routing among $\cdot$/M/1 queues with partial information. Stochastic Models 20 (2004) 149–172 CrossRef
Altman, E., Jimenez, T., Nunez Queija, R. and Yechiali, U., A correction to Optimal routing among $\cdot$/M/1 queues with partial information. Stochastic Models 21 (2005) 981 CrossRef
F. Avram, Analytic solutions for some QBD models (2010)
Hassin, R., On the advantage of being the first server. Management Sci. 42 (1996) 618–623 CrossRef
Haviv, M. and Kerner, Y., The age of the arrival process in the G/M/1 and M/G/1 queues. Math. Methods Oper. Res. 73 (2011) 139–152 CrossRef
Kopzon, A., Nazarathy, Y. and Weiss, G., A push-pull network with infinite supply of work. Queueing Systems: Theory and Application 62 (2009) 75–111 CrossRef
Karlin, S. and McGregor, J.L., The differential equations of birth-and-death processes, and the Stieltjes moment problem. Trans. Am. Math. Soc. 85 (1957) 589–646 CrossRef
Keller-Gehring, W., Fast algorithm for the characteristic polynomial. Theor. Comput. Sci. 36 (1985) 309–317 CrossRef
L. Kleinrock, Queueing Systems 2. John Wiley and Sons, New York (1976)
D.P. Kroese, W.R.W. Scheinhardt and P.G. Taylor, Spectral properties of the tandem Jackson network, seen as a quisi-birth-and-death process, Ann. Appl. Prob. 14 (2004) 2057–2089 CrossRef
D. Liu and Y.Q. Zhao, Determination of explict solutions for a general class of Markov processes, in Matrix-Analytic Methods in Stochastic Models, edited by S. Charvarthy and A.S. Alfa, Marcel Dekker (1996) 343–357
M. Neuts Matrix-Geometric Solutions in Stochastic Models. The John Hopkins University Press, Baltimore (1981)
Ramaswami, V. and Latouch, G., A general class of Markov processes with explicit matrix-geometric solutions. OR Spektrum 8 (1986) 209–218 CrossRef
S.M. Ross Stochastic Processes, 2nd edition, John Wiley and Sons, New York (1996)