No CrossRef data available.
Article contents
On the parallel complexityof the alternating Hamiltonian cycle problem
Published online by Cambridge University Press: 15 August 2002
Abstract
Given a graph with colored edges, a Hamiltonian cycle iscalled alternating if its successive edges differ in color. The problemof finding such a cycle, even for 2-edge-colored graphs, is triviallyNP-complete, while it is known to be polynomial for 2-edge-coloredcomplete graphs. In this paper we study the parallel complexity of finding such a cycle, if any, in 2-edge-colored complete graphs. We givea new characterization for such a graph admitting an alternatingHamiltonian cycle which allows us to derive a parallel algorithm forthe problem. Our parallel solution uses a perfect matching algorithmputting the alternating Hamiltonian cycle problem to the RNC class. Inaddition, a sequential version of our parallel algorithm improves thecomputation time of the fastest known sequential algorithm for thealternating Hamiltonian cycle problem by a factor of $O(\sqrt {n} )$ 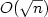 .
.
- Type
- Research Article
- Information
- Copyright
- © EDP Sciences, 1999


