Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-28T14:41:33.729Z Has data issue: false hasContentIssue false
  • English
  • Français

WIGGLE MATCHING WITH CORRELATIONS

Published online by Cambridge University Press:  18 January 2022

Paul Muzikar Open the ORCID record for Paul Muzikar [Opens in a new window]  and
Timothy J Heaton
Paul Muzikar*
Affiliation:
Department of Physics and Astronomy, Purdue University West Lafayette, IN47907, USA
Timothy J Heaton
Affiliation:
School of Mathematics and Statistics, University of SheffieldSheffieldS3 7RH, UK
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Wiggle matching is an important and powerful technique in radiocarbon dating that can be used to improve the precision of calendar age estimates. All radiocarbon determinations require calibration to provide calendar age estimates. This calibration is achieved by comparing the determinations against a calibration curve 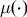$\mu ( \cdot )$ to calculate the probability the sample arises from any particular calendar age t. Wiggle matching involves the calibration of a set of radiocarbon determinations taken from samples with known separations between their calendar ages. Since the calendar age separations between samples are known, all the calendar ages are known functions of one particular age, 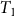${T_1}$ — commonly the most recent calendar age. Dating the sequence then reduces to considering 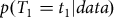$p({T_1} = {t_1}|data)$, the probability of the calendar age 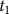${t_1}$ given the set of radiocarbon determinations. In previous work, a Bayesian approach has been used to derive a nice formula for this quantity under the assumption we have independent pointwise estimates of the calibration curve 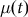$\mu (t)$. In this paper, we derive a generalization of this formula showing how to incorporate covariance information from the calibration curve under an assumption of multivariate normality.

Keywords

Bayesian analysisradiocarbon dating
Type
Technical Note
Information
Radiocarbon , Volume 64 , Issue 1 , February 2022 , pp. 187 - 194
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press for the Arizona Board of Regents on behalf of the University of Arizona

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Adolphi, F, Muscheler, R, Friedrich, M, Guttler, D, Wacker, L, Talamo, S, Kromer, B. 2017. Radiocarbon calibration uncertainties during the last deglaciation: insights from new floating tree-ring chronologies. Quaternary Science Reviews 170:98–108.CrossRefGoogle Scholar
Bard, E, Menot, G, Rostek, F, Licari, L, Boning, P, Edwards, R, Cheng, H, Wang, Y, Heaton, T. 2013. Radiocarbon calibration/comparison records based on marine sediments from the Pakistan and Iberian margins. Radiocarbon 55(4):1999–2019.CrossRefGoogle Scholar
Blackwell, PG, Buck, CE. 2008. Estimating radiocarbon calibration curves. Bayesian Analysis 3(2):225–248.CrossRefGoogle Scholar
Bronk Ramsey, C. 2015. Mathematics and archaeology. Bayesian approaches to the building of archaeological chronologies. Taylor and Francis. p. 272–292.Google Scholar
Bronk Ramsey, C, Heaton, TJ, Schlolaut, G, Staff, RA, Bryant, CL, Brauer, A, Lamb, HF, Marshall, MH, Nakagawa, T. 2020. Reanalysis of the atmospheric radiocarbon calibration record from Lake Suigetsu, Japan. Radiocarbon 62(4):989–999.CrossRefGoogle Scholar
Bronk Ramsey, C, van der Plicht, J, Weninger, B. 2001. Wiggle matching radiocarbon dates. Radiocarbon 43(2A):381–389.CrossRefGoogle Scholar
Butzin, M, Heaton, TJ, Kohler, P, Lohmann, G. 2020. A short note on marine reservoir age simulations used in IntCal20. Radiocarbon 62(4):865–871.CrossRefGoogle Scholar
Cheng, H, Lawrence Edwards, R, Southon, J, Matsumoto, K, Feinberg, JM, Sinha, A, Zhou, W, Li, H, Li, X, Xu, Y, et al. 2018. Atmospheric 14C/12C changes during the last glacial period from Hulu Cave. Science 362(6420):1293–1297.CrossRefGoogle ScholarPubMed
Christen, J, Litton, C. 1995. A Bayesian approach to wiggle-matching. Journal of Archaeological Science 22(6):719–725.CrossRefGoogle Scholar
Heaton, T, Bard, E, Hughen, K. 2013. Elastic tie-pointing-transferring chronologies between records via a Gaussian process. Radiocarbon 55(4):1975–1997.CrossRefGoogle Scholar
Heaton, TJ, Blaauw, M, Blackwell, PG, Bronk Ramsey, C, Reimer, PJ, Scott, EM. 2020. The IntCal20 approach to radiocarbon calibration curve construction: a new methodology using Bayesian splines and errors-in-variables. Radiocarbon 62(4):821–863.CrossRefGoogle Scholar
Heaton, TJ, Blackwell, PG, Buck, CE. 2009. A Bayesian approach to the estimation of radiocarbon calibration curves: the IntCal09 methodology. Radiocarbon 51(4):1151–1164.CrossRefGoogle Scholar
Hughen, K, Heaton, T. 2020. Updated Cariaco Basin 14C calibration dataset from 0–60 cal kyr BP. Radiocarbon 62(4):1001–1043.CrossRefGoogle Scholar
Millard, AR. 2008. Comment on “Estimating radiocarbon calibration curves”. Bayesian Analysis 3(2):255–262.Google Scholar
Niu, M, Heaton, TJ, Blackwell, PG, Buck, CE. 2013. The Bayesian approach to radiocarbon calibration curve estimation: the IntCal13, Marine13, SHCal13 methodologies. Radiocarbon 55(4):1905–1922.CrossRefGoogle Scholar
Pearson, GW. 1986. Precise calendrical dating of known growth-period samples using a curve fitting technique. Radiocarbon 28(2A):292–299.CrossRefGoogle Scholar
Reimer, PJ, Austin, WEN, Bard, E, Bayliss, A, Blackwell, PG, Ramsey, CB, Butzin, M, Cheng, H, Edwards, RL, Friedrich, M, Grootes, PM, Guilderson, TP, Hajdas, I, Heaton, TJ, Hogg, AG, Hughen, KA, Kromer, B, Manning, SW, Muscheler, R, Palmer, JG, Pearson, C, van der Plicht, J, Reimer, RW, Richards, DA, Scott, EM, Southon, JR, Turney, CSM, Wacker, L, Adolphi, F, Büntgen, U, Capano, M, Fahrni, SM, Fogtmann-Schulz, A, Friedrich, R, Köhler, P, Kudsk, P, Miyake, F, Olsen, J, Reinig, F, Sakamoto, M, Sookdeo, A, Talamo, S. 2020. The IntCal20 Northern Hemisphere radiocarbon age calibration curve (0–55 cal kBP). Radiocarbon 62(4):725–757.CrossRefGoogle Scholar
Southon, J, Noronha, AL, Cheng, H, Edwards, RL, Wang, Y. 2012. A high resolution record of atmospheric 14C based on Hulu Cave speleothem H82. Quaternary Science Reviews 33:32–41.CrossRefGoogle Scholar
Turney, CSM, Fifeld, LK, Hogg, AG, Palmer, JG, Hughen, K, Baillie, MGL, Galbraith, R, Ogden, J, Lorrey, A, Tims, SG, Jones, RT. 2010. The potential of New Zealand kauri (Agathis australis) for testing the synchronicity of abrupt climate change during the Last Glacial Interval (60,000–11,700 years ago). Quaternary Science Reviews 29(27):3677–3682.CrossRefGoogle Scholar
Turney, CSM, Palmer, J, Bronk Ramsey, C, Adolphi, F, Muscheler, R, Hughen, KA, Staff, R A, Jones, RT, Thomas, ZA, Fogwill, CJ, Hogg, A. 2016. High-precision dating and correlation of ice, marine and terrestrial sequences spanning Heinrich Event 3: testing mechanisms of interhemispheric change using New Zealand ancient kauri (Agathis australis). Quaternary Science Reviews 137:126–134.CrossRefGoogle Scholar
van der Plicht, J, Bronk Ramsey, C, Heaton, TJ, Scott, EM, Talamo, S. 2020. Recent developments in calibration for archaeological and environmental samples. Radiocarbon 62(4):1095–1117.CrossRefGoogle Scholar