1 INTRODUCTION
The asteroseismology of red giant stars has become a highlight of the CoRoT and Kepler space missions (for general reviews, see e.g. Chaplin & Miglio Reference Chaplin and Miglio2013; García & Stello Reference García, Stello, Tong and García2015). One feature that has made these stars interesting, is the presence of non-radial oscillation modes that reveal properties of the stellar cores. The non-radial modes have a mixed nature, behaving like acoustic (or p) modes in the envelope with pressure acting as the restoring force, and as gravity (or g) modes in the core region with buoyancy being the restoring force (e.g. Bedding Reference Bedding2014). The p- and g-mode cavities are separated by an evanescent zone, which the waves can tunnel through from either side. The exact p- and g-‘mixture’, or flavour, of a mixed mode depends on its frequency and spherical degree, ℓ. Modes with frequencies close to the acoustic resonant frequencies of the stellar envelope tend to be more p-mode like, while those far from the acoustic resonances are much more g-mode like. The latter therefore probe deeper into the stellar interior compared to the former. How much the flavour changes from mode to mode across the acoustic resonances depends on the overall coupling between the envelope and the core. The overall aspects of mode mixing in red giants arising from this coupling is well understood theoretically (Dupret et al. Reference Dupret2009). Observationally, the dipole modes (ℓ = 1) have turned out to be particularly useful probes of the core because of their stronger coupling between core and envelope. The characterisation of dipole mixed modes (Beck et al. Reference Beck2011) led to the discovery that red giant branch stars can be clearly distinguished from red clump stars (Bedding et al. Reference Bedding2011), and to the detection of radial differential rotation (Beck et al. Reference Beck2012). Modes of higher spherical degree are also mixed, but the weaker coupling makes it difficult to observe the modes with strong g-mode flavour. The quadrupole modes (ℓ = 2) we observe, and to a larger degree the octupole modes (ℓ = 3), are therefore on average more acoustic compared to the dipole modes, and hence less sensitive to the stellar core.
One particular observational result about the dipole modes posed an intriguing puzzle. The ensemble study of a few hundred Kepler red giants by Mosser et al. (Reference Mosser2012) showed that a few dozen stars—about 20% of their sample—had significantly lower power in the dipole modes than ‘normal’ stars. However, no significant suppression of higher degree modes was reported, leading to the conclusion only dipole modes were affected.
Recent theoretical work has proposed that the mechanism responsible for the mode suppression results in almost total trapping of the mode energy that leaks into the g-mode cavity (Fuller et al. Reference Fuller, Cantiello, Stello, Garcia and Bildsten2015). They put forward magnetic fields in the core region of the stars as the most plausible candidate for the suppression mechanism. This interpretation was further supported by the observation that mode suppression only occurs in stars above 1.1 M⊙, with an increasing fraction up to 50–60% for slightly more massive stars, all of which hosted convective cores during their main sequence phase; strongly pointing to a convective core dynamo as the source of the mode suppressing magnetic field (Stello et al. Reference Stello, Cantiello, Fuller, Huber, Garcia, Bedding, Bildsten and Aguirre2016). Both Fuller et al. (Reference Fuller, Cantiello, Stello, Garcia and Bildsten2015) and Stello et al. (Reference Stello, Cantiello, Fuller, Huber, Garcia, Bedding, Bildsten and Aguirre2016) focused their analysis on dipole modes. However, the theory by Fuller et al. (Reference Fuller, Cantiello, Stello, Garcia and Bildsten2015) does allow one to predict the magnitude of the suppression for higher degree modes. Agreement with observations of these modes would provide important support for the proposed mechanism.
In this paper, we use 3.5 yrs of Kepler data of over 3 600 carefully selected red giant branch stars to investigate the mode suppression in the non-radial modes of degree ℓ = 1, 2, and 3, and compare theoretical predictions with our observed mode visibilities.
2 THEORETICAL PREDICTIONS
We use the Modules for Experiments in Stellar Evolution (mesa, release #7456, Paxton et al. Reference Paxton, Bildsten, Dotter, Herwig, Lesaffre and Timmes2011, Reference Paxton2013, Reference Paxton2015) to compute stellar evolution models of low-mass stars from the zero age main sequence to the tip of the red giant branch. Non-rotating models have been computed using an initial metallicity of Z = 0.02 with a mixture taken from Asplund et al. (Reference Asplund, Grevesse, Sauval, Barnes and Bash2005) and adopting the opal opacity tables (Iglesias & Rogers Reference Iglesias and Rogers1996). We calculate convective regions using the mixing-length theory with αMLT = 2.0. The boundaries of convective regions are determined according to the Schwarzschild criterion.
We calculate the expected visibilities for dipole, quadrupole, and octupole modes in models with masses 1.1, 1.3, 1.5, 1.7, and 1.9M⊙ following Fuller et al. (Reference Fuller, Cantiello, Stello, Garcia and Bildsten2015). According to the theory, the ratio of suppressed mode power to normal mode power is
 $$\begin{equation}
\frac{V_{\rm sup}^2}{V_{\rm norm}^2} = \bigg [ 1 + \Delta \nu \, \tau \,T^2 \bigg ]^{-1} \, ,
\end{equation}$$
$$\begin{equation}
\frac{V_{\rm sup}^2}{V_{\rm norm}^2} = \bigg [ 1 + \Delta \nu \, \tau \,T^2 \bigg ]^{-1} \, ,
\end{equation}$$
where Δν is the large frequency separation, τ is the radial mode lifetime [measurable from the observed frequency power spectrum (e.g. Corsaro, De Ridder, & García Reference Corsaro, De Ridder and García2015)], and T is the wave transmission coefficient through the evanescent zone. T is calculated via
 $$\begin{equation}
T = \exp \bigg [ - \int ^{r_2}_{r_1} dr \sqrt{ -\frac{ \big ( L_\ell ^2 - \omega ^2 \big ) \big (N^2 - \omega ^2 \big ) }{v_{\rm s}^2 \omega ^2} } \bigg ] \,.
\end{equation}$$
$$\begin{equation}
T = \exp \bigg [ - \int ^{r_2}_{r_1} dr \sqrt{ -\frac{ \big ( L_\ell ^2 - \omega ^2 \big ) \big (N^2 - \omega ^2 \big ) }{v_{\rm s}^2 \omega ^2} } \bigg ] \,.
\end{equation}$$
Here, r 1 and r 2 are the lower and upper boundaries of the evanescent zone, L 2 ℓ = l(l + 1)v s 2/r 2 is the Lamb frequency squared, N is the buoyancy frequency, ω is the angular wave frequency, and vs is the sound speed. We calculate Δν and the frequency of maximum power, νmax, using the scaling relations of Brown et al. (Reference Brown, Gilliland, Noyes and Ramsey1991) and Kjeldsen & Bedding (Reference Kjeldsen and Bedding1995) with the solar references values, Δν⊙ = 135.1μHz and νmax ⊙ = 3090μHz.
3 DATA ANALYSIS
3.1. Sample selection
Our initial selection of stars was based on the analysis by Stello et al. (Reference Stello2013) of 13 412 red giants from which we adopt their measurements of Δν and νmax, as well as their estimates of stellar mass based on the combination of those seismic observables with photometrically derived effective temperatures using scaling relations (see Stello et al. Reference Stello2013, for details). In order to select only red giant branch stars from this sample, we follow the approach by Stello et al. (Reference Stello, Cantiello, Fuller, Huber, Garcia, Bedding, Bildsten and Aguirre2016). We selected all 3 993 stars with νmax > 50 μHz and M < 2.1M⊙, which based on stellar models is expected to select only red giant branch stars (e.g. Stello et al. Reference Stello2013). However, this selection does not take measurement uncertainties in νmax and M into account, possibly introducing some helium-core burning stars into our sample towards the lower end of the νmax bracket. We therefore performed a few additional steps to further reduce the possible ‘contamination’ by helium-burning stars in our sample.
First, we derived the offset from zero of the harmonic series of radial modes, known as ε in the asymptotic relation, ν = Δν(n + ℓ/2 + ε), where ν is the mode frequency and n is the radial order. This offset is known to be different for helium-burning stars (Kallinger et al. Reference Kallinger2012; Christensen-Dalsgaard et al. Reference Christensen-Dalsgaard, Silva Aguirre, Elsworth and Hekker2014) relative to red giant branch stars of similar density, and hence has diagnostic power to distinguish the two types of stars. To measure ε, we calculated frequency power spectra for each star using long-cadence (Δt ≃ 29.4min) Kepler data obtained between 2009 May 2 and 2012 October 3, corresponding to observing quarters 0–14, or a total of about 54 000 data points per star. We used the method by Huber et al. (Reference Huber, Stello, Bedding, Chaplin, Arentoft, Quirion and Kjeldsen2009) to fit and remove the background noise profile of the spectra, and then selected the central ± 2Δν spectral range around νmax, which we folded with an interval of Δν. The folded spectrum was smoothed by a Gaussian function with a full-width-half-maximum of 0.1Δν, and correlated with a model of the spectrum (Figure 1).

Figure 1. (a) Folded and smoothed spectrum (black curve) of the central 4Δν-wide region around νmax of a normal star (KIC2141255). Regions dominated by modes of degrees, ℓ = 0, 1, 2, and 3 are indicated. The red curve shows the model shifted to the position resulting in the largest correlation with the data. (b) Correlation versus shift between model and data. (c) and (d) The same as (a) and (b), but for a star with suppressed non-radial modes (KIC4348666).
Each spherical degree in the model was described by a Lorentzian profile with relative heights of 1.0, 0.5, and 0.8 for the ℓ = 0, ℓ = 1, and ℓ = 2 modes, and widths of 5, 10, and 5% of Δν, respectively. The Lorentzian profiles were centred relative to each other with the one representing quadrupole modes being 0.12Δν to the left of the radial mode profile, and the one representing the dipole modes being 0.52Δν to the right of the radial mode following the results by Huber et al. (Reference Huber2010) (see Figure 1). The shift between data and model providing the largest correlation was adopted as εmod1. Only the 3 721 stars with ε within ± 0.1 of the Δν-ε relation by Corsaro et al. (Reference Corsaro2012) (ε = 0.634 + 0.63log(Δν)) were kept in our sample (see Figure 2).

Figure 2. Δν versus ε of the 3,993 red giants from the Stello et al. (Reference Stello2013) sample with νmax > 50μHz and M < 2.1M⊙. The solid red curve shows the relation by Corsaro et al. (Reference Corsaro2012), and the dotted red curves show the relation shifted by ± 0.1.
Second, we cross matched our remaining sample with the stars identified as burning helium by Stello et al. (Reference Stello2013) and Mosser et al. (Reference Mosser2014) based on their dipole-mode period spacings. We found 86 helium-burning stars this way, which we removed. We note that all but eight of these helium-burning contaminants had νmax < 70μHz (and all < 85μHz). Although our remaining sample could potentially still include some helium-burning stars if they were not in the Stello et al. (Reference Stello2013) and Mosser et al. (Reference Mosser2014) samples, the above cross match indicates such contaminants would most likely have νmax < 70μHz. As a final check, we visually inspected the power spectra of the remaining sample (3 635 stars), which led to the removal of 24 stars that appeared to be helium-core burning or had spectra of such poor quality (low signal-to-noise or bad window function) that the stellar classification was ambiguous.
3.2. Mode visibility measurements
To measure the mode visibilities, we first needed to identify the regions in the power spectra dominated by the different modes. Here, we used the ε values found in the previous step (Section 3.1) to locate the four central radial modes closest to νmax, and followed the approach by Stello et al. (Reference Stello, Cantiello, Fuller, Huber, Garcia, Bedding, Bildsten and Aguirre2016) for masking the parts of the spectra dominated by ℓ = 0, ℓ = 1, ℓ = 2, and ℓ = 3 modes. The regions we chose were ε − 0.06 < (ν/Δνmod1) < ε + 0.10 for ℓ = 0, ε + 0.25 < (ν/Δνmod1) < ε + 0.78 for ℓ = 1, ε − 0.22 < (ν/Δνmod1) < ε − 0.06 for ℓ = 2, and ε + 0.10 < (ν/Δνmod1) < ε + 0.25 for ℓ = 3. In this way, the entire 4Δν-wide central part of the spectrum was divided up into distinct segments associated with either ℓ = 0, ℓ = 1, ℓ = 2, or ℓ = 3 modes. In Figure 3, we show a couple of representative spectra with the results of the masking, identifying the different mode degrees. See also Figure 1 in Stello et al. (Reference Stello, Cantiello, Fuller, Huber, Garcia, Bedding, Bildsten and Aguirre2016) who used the exact same scheme.
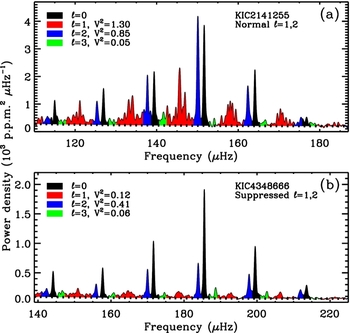
Figure 3. Representative power spectra of two red giants from our sample. For clarity, the spectra have been smoothed by 0.03Δν, which partly merges the power from individual mixed modes into one broad peak around each acoustic resonance. The coloured regions indicate the integrated power associated with each mode of degree ℓ = 0, 1, 2, and 3. The horizontal-dashed curves shows the estimated noise profile (a) Star with normal mode visibility, V 2, of the non-radial modes. (b) Star with low mode visibilities in both dipole and quadrupole modes, but normal octupole mode visibility.
Finally, the mode visibilities, V 2, of the non-radial modes were derived as the ratio of the total mode power of the segments associated with a given degree relative to the total radial mode power. For this, we used the background-corrected spectra described in Section 3.1. We note that the uncertainty in the background estimation introduces measurement scatter on top of the intrinsic spread in the visibilities, potentially pushing intrinsically low values of V 2 below zero. Rejecting those stars or artificially pushing them up to V 2 = 0 would be statistically incorrect and bias our measurements of the average V 2.
4 RESULTS
4.1. The dipole modes revisited
In Figure 4, we show our measurements of the dipole mode visibility as function of νmax. We denote the stars below the dotted line as the dipole-suppressed sample, as opposed to the ‘normal’ stars. As shown in Fuller et al. (Reference Fuller, Cantiello, Stello, Garcia and Bildsten2015) and Stello et al. (Reference Stello, Cantiello, Fuller, Huber, Garcia, Bedding, Bildsten and Aguirre2016), the predicted visibilities of the suppressed dipole modes (solid lines) match the observations remarkably well, and with normal stars on average being less massive. Here, we show that the prediction for the dipole-mode suppression is insensitive to stellar mass for the typical mass range of the Kepler red giants (the solid black curves fall almost on top of each other), which is also what we observe in the data. The slight dependence on mode lifetime, τ, is illustrated by comparing the black curves (all τ = 20d) with the gray curves based on a 1.7M⊙ track just above (τ = 10d) and below (τ = 40d) the black curves. We find no variation in the average visibility (V 2 ℓ = 1 = 1.35) and its scatter for the normal stars as a function on νmax.

Figure 4. Visibility of dipole modes (V 2 ℓ = 1) for 3 611 red giants below the red giant branch luminosity bump. Stars evolve from right to left, and their approximate logg values are shown on the top axis. The rms scatter in V 2 ℓ = 1 is 0.26 (or 20%) for the normal stars. The colour of each symbol indicates the stellar mass according to the scale on the right-hand side. The solid black lines are the predicted visibilities from 1.1, 1.3, 1.5, 1.7, and 1.9 M⊙ models adopting an average mode lifetime of 20 d in agreement with Corsaro et al. (Reference Corsaro, De Ridder and García2015) (Section 2). The solid gray curves are the predicted visibilities from 1.7 M⊙ models for mode lifetimes of 10 d (highest V 2 ℓ = 1) and 40 d (lowest V 2 ℓ = 1). The dotted fiducial line, adopted from Stello et al. (Reference Stello, Cantiello, Fuller, Huber, Garcia, Bedding, Bildsten and Aguirre2016), separates dipole-suppressed and normal stars. The observed dipole visibilities are identical to those by Stello et al. (Reference Stello, Cantiello, Fuller, Huber, Garcia, Bedding, Bildsten and Aguirre2016).
In an attempt to determine if the dipole-suppressed sample is somehow distinct other than by their mass (Stello et al. Reference Stello, Cantiello, Fuller, Huber, Garcia, Bedding, Bildsten and Aguirre2016), we do not find them to be statistically different in terms of their distance and position on sky. If we focus on the mass range 1.5 < M/M⊙ < 1.8, where we find the highest number and fraction (50–60%) of dipole-suppressed stars (Stello et al. Reference Stello, Cantiello, Fuller, Huber, Garcia, Bedding, Bildsten and Aguirre2016), the dipole-suppressed sample is on average slightly more metal poor (by 0.045 ± 0.017 dex) than the normal stars, and slightly hotter (by 26.9 ± 8.9K) (based on SDSS-APOGEE DR12, Alam et al. Reference Alam2015).
4.2. The quadrupole and octupole modes
The quadrupole and octupole visibilities are shown in Figures 5(a) and (b), respectively. Here, we only show the dipole-suppressed sample as filled symbols, to make it easier to distinguish them from the normal population shown as empty symbols. While less dramatic than the dipole modes, the quadrupole modes show significant reduction in mode power for the dipole-suppressed sample. The least evolved stars (210 <νmax/μHz < 240) show on average V 2 ℓ = 2 = 0.350 ± 0.053, compared to V 2 ℓ = 2 = 0.688 ± 0.003 for all the normal stars, corresponding to 49% reduction in power. Although there is overall good agreement between the predictions and the observations, the trend of the visibility as a function of νmax is predicted to be steeper than observed if we, as done here, assume a fixed mode lifetime along the red giant branch [Figure 5(a)]. We used a lifetime of 20d, which is representative for the average value found by Corsaro et al. (Reference Corsaro, De Ridder and García2015). This assumption could, at least partly, explain the discrepancy, because the observed mode lifetimes are most likely increasing as red giants evolve towards lower νmax and lower T eff. The variation in mode lifetime was found to be roughly 50% by Corsaro et al. (Reference Corsaro, De Ridder and García2015, their Figure 7) across a sample spanning a νmax range of ~ 110–160μHz (their Table A.2). Our sample span a much larger νmax range, and for reference we therefore also show the 1.7M⊙ tracks in gray with factors of two difference in mode lifetime; 10 and 40 d, respectively. Based on this, we conclude that an increasing mode lifetime along the red giant branch could possibly explain the apparent discrepancy of the predicted versus observed trend seen in Figure 5(a). A mode lifetime of ~ 15d at νmax = 200μHz and a lifetime of ~ 30d at νmax = 70μHz would provide a better match to the data. However, we note that the predicted visibilities of the suppressed sample depends somewhat on the overshoot beyond classical Schwarzschild implemented in the stellar models (Cantiello et al. Reference Cantiello, Fuller and Bildsten2016), so we defer a more thorough analysis to future work, but point out here the possibility of constraining either the mode lifetime or the overshoot given independent measurements of the other.

Figure 5. (a) Visibility of quadrupole modes for the same stars as shown in Figure 4. The notation follows that of Figure 4 except only the dipole-suppressed stars (those below the dotted line in Figure 4) are shown by filled symbols. The observed rms scatter in V 2 ℓ = 2 is 0.14 (or 20%) for the normal stars. (b) The same as panel (a) but for octupole modes. Here, the observed V 2 ℓ = 3 scatter is 0.05 (84%).
Turning to the octupole modes [Figure 5(b)], we see no significant effect of the suppression, as anticipated by theory (solid black curves) because they are almost purely acoustic envelope modes. We find the average visibilities to be V 2 ℓ = 3 = 0.0591 ± 0.0009 for the normal stars, and V 2 ℓ = 3 = 0.0577 ± 0.0018 for the dipole-suppressed sample, which are the same within 1σ. In Figure 5(b), we do not show the tracks of different mode lifetimes because they are essentially indistinguishable from the black curves.
4.3. Discussion
Both the evolution of the predicted mode visibility as a function of νmax (for fixed spherical degree) and its dependence on mode degree (for fixed νmax) are essentially determined by the difference in coupling between the core and envelope as the star evolves (or as seen by modes of different degree). The key aspect of this predicted behaviour is that there is perfect trapping of the mode energy leaking into the core by the suppression mechanism. Hence, given the agreement reported here between theory and observations for both ℓ = 2 and ℓ = 3 modes, in addition to what is seen for dipole modes, supports this notion that the mode suppression mechanism indeed traps almost, if not, all the energy that leaks into the core region.
The theoretical predictions presented in Figures 4 and 5 are derived relative to non-suppressed stars, and are hence scaled to the observed average visibilities of the normal stars. We note that the absolute scale of the observed visibilities reported here are not directly comparable with expectations for the normal stars (Ballot, Barban, & van’t Veer-Menneret Reference Ballot, Barban and van’t Veer-Menneret2011) because we simply integrated the power over fixed regions of the spectrum in terms of Δν. Due to the presence of mixed modes, which strictly speaking exist across the entire spectrum, small amounts of power (from gravity-dominated modes far from the acoustic resonant frequencies) from one degree of modes will be present in the regions that we associate with modes of another degree. Direct comparisons would therefore need to be based on simultaneous fitting of model profiles to all the modes in the spectrum, which is currently not practically possible for large numbers of stars (Corsaro et al. Reference Corsaro, De Ridder and García2015). Similarly, any differences between the average visibilities reported here and those by Mosser et al. (Reference Mosser2012), are most likely due to slight different choices for the mode integration regions in the two studies.
5 SUMMARY AND OUTLOOK
We have measured oscillation mode power in over 3 600 red giant stars, and compared our results to theoretical predictions based on the ‘magnetic greenhouse’ mechanism proposed by Fuller et al. (Reference Fuller, Cantiello, Stello, Garcia and Bildsten2015) for dipole mode suppression. Our results from modes of spherical degrees ℓ ⩽ 3, provide strong support for one of the main assertions of the theory behind the mode suppression—all mode energy leaking into the g-mode cavity of a star is efficiently trapped or dissipated. Specifically, we confirm the up to almost 100% suppression for dipole modes previously shown and measure for the first time up to 49% suppression on average of the quadrupole modes and no suppression of the octupole modes. We find it likely that a variation in the mode lifetime along the red giant branch could explain the small difference in slope between our prediction and the observations in the V 2 ℓ = 2 versus νmax diagram. However, the variation required needs to be confirmed by measurements of the mode lifetime of radial modes for a robust sample of stars with νmax around 220 and 70 μHz.
Further tests of the magnetic greenhouse effect could be implemented with determinations of the lifetimes of the suppressed dipole modes, or the measurement of suppressed dipole mode visibilities in helium-burning clump stars (Cantiello et al. Reference Cantiello, Fuller and Bildsten2016).
ACKNOWLEDGEMENTS
We acknowledge the entire Kepler team, whose efforts made these results possible. D.S. is the recipient of an Australian Research Council Future Fellowship (project number FT140100147). J.F. acknowledges support from NSF under grant no. AST-1205732 and through a Lee DuBridge Fellowship at Caltech. R.A.G. acknowledge the support of the European Community’s Seventh Framework Programme (FP7/2007-2013) under grant agreement No. 269194 (IRSES/ASK), the ANR- IDEE (n ANR-12-BS05-0008), and from the CNES. D.H. acknowledges support by the Australian Research Council’s Discovery Projects funding scheme (project number DE140101364) and support by the National Aeronautics and Space Administration under Grant NNX14AB92G issued through the Kepler Participating Scientist Program. This project was supported by NASA under TCAN grant number NNX14AB53G, and the NSF under grants PHY 11-25915 and AST 11-09174. Funding for the Stellar Astrophysics Centre is provided by The Danish National Research Foundation (Grant agreement no.: DNRF106). The research is supported by the ASTERISK project (ASTERoseismic Investigations with SONG and Kepler) funded by the European Research Council (Grant agreement no.: 267864).








