Stellar Populations and the Star Formation Histories of LSB Galaxies: IV Spitzer Surface Photometry of LSB Galaxies

Abstract

Surface photometry at 3.6 μm is presented for 61 low surface brightness (LSB) galaxies (μ_o<19 3.6 μm mag arcsecs⁻²). The sample covers a range of luminosity from −11 to −22 in M_3.6 and size from 1 to 25 kpc. The morphologies in the mid-IR are comparable to those in the optical with 3.6 μm imaging reaches similar surface brightness depth as ground-based optical imaging. A majority of the resulting surface brightness profiles are single exponential in shape with very few displaying upward or downward breaks. The mean V − 3.6 colour of LSB is 2.3 with a standard deviation of 0.5. Colour-magnitude and two-colour diagrams are well matched to models of constant star formation, where the spread in colour is due to small changes in the star formation rate (SFR) over the last 0.5 Gyrs as also suggested by the specific SFR measured by Hα.

1 INTRODUCTION

The primary characteristic of a galaxy is its luminosity and the deduced stellar mass from that luminosity. Of secondary interest is how that luminosity is distributed (again, a proxy for the stellar mass distribution) and galaxy colour, which reflect the properties of the underlying stellar population. The run of luminosity with radius (surface brightness profiles) continue to be the most direct method of deriving the size, luminosity, and density scale parameters that are key to understanding the details of galaxy formation. The total stellar mass and its distribution, as given by surface brightness profiles, also play important roles in the various scaling relations between galaxy types. For example, the Tully–Fisher relation (TF; Tully & Fisher 1977) is one of the strongest correlations in extragalactic astronomy. It provides a vital constraint on galaxy formation theory (e.g., Eisenstein & Loeb 1996; McGaugh & de Blok 1998; Courteau & Rix 1999; van den Bosch 2000; Navarro & Steinmetz 2000; Mo & Mao 2000, 2004).

The dominant uncertainty in the TF relation is the deduction of stellar mass from luminosity. In order to constrain the luminosity to stellar mass relationship, our stellar population models agree that longer wavelength observations more accurately map into stellar mass (Bruzual & Charlot 2003). Empirically, the scatter in the TF relation declines as one goes from blue to red to NIR wavelengths (Verheijen 2001), consistent with the expected decrease in scatter in M/L _*. However, low surface brightness (LSB) galaxies are, by definition, very faint in luminosity density, typically well below the natural sky brightness. This is particularly a problem at near-IR wavelengths where the sky brightness from the ground is several magnitudes brighter than the sky at near-UV wavelengths. To this end, the longer wavelength IRAC (InfraRed Array Camera) data from the Spitzer orbiting telescope provides a unique probe of stellar mass, dust, and star formation, useful for testing whether extinction or fluctuations in the star formation rate (SFR) cause deviations from the TF relation.

The goal of this paper, the fourth in our series to understand the star formation history of LSB galaxies, is to present the 3.6 μm imaging for a sample of high surface brightness (HSB) and LSB galaxies obtained during the 2009/2010 observing seasons. The data was acquired as part of a study of the baryonic TF relation (McGaugh & Schombert 2013) where the total luminosity of a galaxy at 3.6 μm provides a more accurate measure of stellar mass and an independent estimate of the colour-mass to light ratio. During data reduction it was determined that the images were comparable in depth to optical imaging, and open to a full surface photometric analysis for direct comparison to optical values obtained in Paper I (Schombert, Maciel, & McGaugh 2011).

2 OBSERVATIONS

2.1 Sample properties

Selection criteria based on magnitudes preferentially miss LSB galaxies because much of their integrated light resides below the detection threshold of wide area surveys (McGaugh 1994). However, the low sky afforded by Spitzer observations is ideally suited to the observation of LSB galaxies and is vastly superior to ground-based observations in the JHK bands, which still lag well behind other types of data for these systems because of the obvious technical challenges. To this end, our sample was designed to explore a wide swath of under-sampled parameter space in the mid-IR, probing a large region in galaxy mass and gas fraction as well as surface brightness.

The sample presented herein are a combination of LSB galaxies, selected for Spitzer cycle 9 observing based on their central surface brightness and existing optical and Hα imaging, and a small subset of comparison HSB galaxies. The HSB galaxies were taken from McGaugh (2005), selected for their large mass and observed for a baryonic TF cycle 5 program. All the LSB galaxies are selected from the Schombert F and D LSB catalogues (Schombert & Bothun 1988; Schombert et al. 1992; Schombert et al. 1995) with some additional, previously known, LSB UGC (Uppsala General Catalogue) galaxies. All the LSB galaxies have central B surface brightness μ _o >23 mag arcsecs⁻², which differs from previous Spitzer LSB programs which usually observed intermediate surface brightness galaxies (22<μ _o <23 mag arcsecs⁻²). The basic characteristics of the entire sample are found in Tables 1 and 2. All the photometry (found in Tables 3 and 4) presented herein were corrected for Galactic extinction using the extinction maps from Schlegel, Finkbeiner, & Davis (1998) and the extinction curve of Li & Draine (2001). Redshifts are determined from previous HI work (Eder & Schombert 2000; Schombert et al. 1992) and used to derive distances based on the CMB (Cosmic Microwave Background) reference frame or tabulated in the Extragalactic Distance Database (Tully et al. 2009). Stellar and gas masses, plus other optical values (such as L _Hα), are taken from Paper I (Schombert et al. 2011).

Table 1. LSB sample morphology.

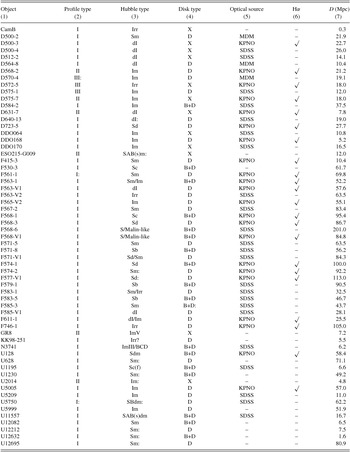
Note. – (1) Galaxy name. (2) Surface brightness profile type; Erwin et al. (2008). (3) Hubble type from Schombert et al. (1992, 1997). (4) Surface brightness profile structure: D = disk, B+D = bulge+disk, X = unknown. (5) Source of optical data. (6) Hα images available. (7) Distance in Mpc from Tully et al. (2009).

Table 2. HSB sample morphology.

Table 3. LSB photometric properties.

Note. – (1) Galaxy name. (2) Apparent magnitude at 3.6 μm. (3) V−3.6 colour, corrected from g for SDSS data (4) Holmberg radius in kpc. (5) Central 3.6-μm surface brightness (mag arcsecs⁻²). (6) Stellar mass. (7) Gas mass. (8) Baryon mass (stars+gas). (9) Gas fraction.

Table 4. HSB photometric properties.

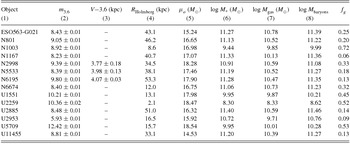
Note. – (1) Galaxy name. (2) Apparent magnitude at 3.6 μm. (3) V−3.6 colour, corrected from g for SDSS data (4) Holmberg radius in kpc. (5) Central 3.6-μm surface brightness (mag arcsecs⁻²). (6) Stellar mass. (7) Gas mass. (8) Baryon mass (stars+gas). (9) Gas fraction.

The range in absolute 3.6 μm magnitude and galaxy size can be found in the top panel of Figure 1. Determination of these parameters is described in Section 3.1, and comparison to optical values can be made with the knowledge that the mean V − 3.6 colour is 2.3 for disk galaxies. The LSB galaxies range from −10 to −22 M _3.6, whereas the HSB galaxies range from −18 to −26. As the HSB subset was selected for their high rotation values (i.e., high mass) to explore the baryonic TF relation, it is not surprising to find that they fill the bright end of the sequence. The brightest galaxy in our sample is F568-6, a supergiant Malin cousin (Bothun et al. 1990). Size, as given by the Holmberg radius, scales with total magnitude, such that the smallest galaxy in the sample (Cam B) has a radius of 0.2 kpc. The typical LSB galaxy ranges from 1 to 10 kpc, which encompasses dwarfs and normal-sized disks. Most of the HSB galaxies are greater than 30 kpc, i.e., Milky Way-sized systems, again due to their selection for high mass.

Figure 1. The top panel displays absolute 3.6-μm magnitude versus the 3.6-μm Holmberg radius. The blue symbols are the LSB galaxies and the red symbols are the HSB sample from our baryonic TF project (McGaugh et al. 2010). The largest galaxy in the sample is F568-6, a supergiant Malin cousin, the smallest is Cam B. The linear relationship between size and luminosity is evident. The bottom panel displays central surface brightness (μ _O , based on exponential fits to the surface brightness profile) versus gas fraction ( $f_g = M_{\text{gas}}/M_{\text{gas}}+M_*$ ). While presenting a wide range in f_g , the highest f_g galaxies are low in surface brightness. Galaxies with f_g > 0.5 are defined as ‘gas-rich’.

The bottom panel in Figure 1 displays one of the primary differences between LSB and HSB, the gas fraction defined as the gas mass of a galaxy (HI plus H₂ and He) divided by the total mass of the galaxy in stars and gas (i.e., baryons). Figure 1 displays what is well known about LSB galaxies (McGaugh & de Blok 1997; Schombert et al. 1995) that f_g rises with lower central surface brightness, although there is only a weak correlation between f_g and μ _o for there exist several LSB galaxies with gas fractions similar to HSB galaxies. We define the phrase ‘gas-rich’ for those galaxies with f_g values above 0.5 and a majority of LSB galaxies (81%) are gas-rich. Thus, while LSB galaxies are difficult to detect at wavelengths where stellar light dominates, they are often quite bright at 21 cm, i.e., neutral hydrogen (Schombert et al. 1992).

2.2 Detector characteristics

The images used in this study were obtained with the Spitzer IRAC. Briefly, IRAC is a four-channel camera that provides simultaneous 5.2 by 5.2 arcmin images at 3.6, 4.5, 5.8, and 8 μm. Two adjacent fields of view are imaged in pairs (3.6 and 5.8 μm; 4.5 and 8.0 μm) using dichroic beamsplitters. All four detector arrays in the camera are 256 by 256 pixels in size, with a pixel size of 1.2 by 1.2 arcsecs.

Our primary data was taken in the 3.6 μm band, whose filter centres at 3.55 μm and covers between 3.1 and 3.9 μm a nearly constant transmission. The maximum exposure time of 100 s was used for each observation, with 24 frames taken for each galaxy for a total of 2 400 s of integration per pixel. The frames were obtained using a 12-point Reuleaux pattern in a 1/2 subpixel dither. The resulting pixels were 0.61 arcsecs in resolution. The frames were flat-fielded and calibrated using the standard Spitzer pipeline. As all our objects were small relative to the field of view, no geometric or spatial flux corrections were applied. The FWHM of the PSF (point spread function) was 1.7 arcsecs for 3.6- and 4.5-μm detectors. No corrections were made for the pixel phase effect as our galaxies are much larger in angular size than any inter-pixel effects. The diffuse light component is removed by our sky procedures.

Photometric calibration is supplied by the Spitzer processing pipeline and has an estimated zero-point error of less than 2% (Reach et al. 2005). However, the true photometric error will be strongly dependent on the knowledge of the correct sky values for each frame, as has always been true for LSB photometry (Schombert et al. 2011). The sky brightness error will have two major components, the pixel-to-pixel noise in the detector pixels and the flatness of the image on the scale of the object to be studied.

As has been successful in our past surface photometry work (Schombert 2011), we have used a sky box technique to determine the absolute sky value and its uncertainty. This technique uses visually selected regions of the galaxy image that are free of contaminating stars and background galaxies. Typically 10 to 20 boxes of 20 × 20 pixels are used in these calculations. For 90% of the galaxy frames in our sample, the sky brightness varied between 20 and 23 AB mags with a mean of 21.0 (where a 0 AB magnitude object has a flux of 280.9 Jys at 3.6 μm). The mean error on the sky was 2.2%, but 80% of the sample had a sky noise of less than 3%. This error dominates all other sources of error in our surface photometry and aperture magnitudes, and is used to assign the uncertainty in all photometric values.

The mean sky value of 21 mag arcsecs⁻² at 3.6 μm is 2.5 mags darker than the optical night sky at our best ground observatories. Thus, where the best optical surface photometry reaches a depth of 28 to 29 V mag arcsecs⁻² (Schombert 1988), it is not uncommon in this sample for the mid-IR data to reach 25 mag arcsecs⁻² at 3.6 μm with error bars of less than 0.5 mags (this corresponds to 0.4 L _⊙ pc⁻²). This is equivalent to optical photometry, but at least 4 mags fainter than ground-based IR surface photometry (e.g., Galaz et al. 2002).

2.3 Frame cleaning

Perhaps the most salient difference between optical and Spitzer imaging is the sharp increase in the number of point sources, not associated with the galaxy of interest, visible in each frame. Figure 2 displays a comparison of 150-s V image (taken with the KPNO 2.1 m) and a 2 400-s Spitzer IRAC 3.6-μm image. The number of point sources in the 3.6-μm image is a factor of 10 greater than the number in the V image, although this is expected from early Spitzer number counts (Fazio et al. 2004). We have matching HST WFC3 imaging of one object in our sample (F415-3), and comparison with those images reveals that (1) bright sources in common with the V and Spitzer images are mostly galactic stars or unresolved nearby galaxies, and (2) faint sources found only the 3.6-μm images are background galaxies, either resolved in the WFC3 frames or sufficiently faint as to be below any galactic star magnitude limit.

Figure 2. Optical V (left) and Spitzer 3.6-μm (right) images for LSB galaxy F568-1. The V image is a 600-s exposure from Kitt Peak National Observatory's (KPNO's) 2.1m (plate scale of 0.6 arcsecs per pixel), the 3.6-μm image is based on a 2 400-s exposure of the same plate scale. The top panels display the uncleaned images, note the larger number of point sources in the 3.6-μm frame (background galaxies) compared to the V frame. The bottom panels display the results of the point source cleaning algorithm which are designed to clean objects not associated with structure in the galaxy itself. All features associated with Hα emission were preserved.

While the percentage of the image frame contaminated by point sources is still a small fraction of the total number of pixels (typically less than 10%), there is a much higher probability that a significant portion of the galaxy image has contaminating point sources compared to V images (although it begs the question that these same sources are interfering with V images in a fashion that is not visible in the V frames).

There are three salient issues for the larger number of contaminating point sources in the Spitzer images: (1) how the point sources interfere with isophote fitting, (2) how much of the galaxy luminosity is contaminated by stellar objects, and (3) how does the observer distinguish between unresolved galaxy features (clusters, Hii regions, etc.) and contaminating point sources. The first issue can be resolved by masking the more obvious stellar features, then allowing the ellipse fitting algorithms to automatically remove pixels above and below a set threshold. Even in small LSB galaxies, there are a sufficient number of remaining pixels to determine the mean isophote value.

The second issue can be mitigated by using the measured isophote values to refill the masked pixels with galaxy light. For small masked areas in the outer regions, this is a simple process with little increase in the uncertainties on the aperture magnitudes. Large masked areas in the core region are most problematic. Fortunately, most LSB galaxies are more symmetric in the core regions, such that filled in masked areas appear visually to be sufficient. Galaxies with large contaminating objects in their cores were simply discarded from our sample.

The third issue, discriminating foreground stars (or background galaxies) from real point-like objects in the galaxies (e.g., unresolved clusters or knots), is the most difficult to replicate in an automatic script. For this study we have followed three guidelines: (1) any feature associated with an enhanced region of surface brightness (i.e., a spiral arm or bulge) was not removed, (2) any feature visible in our deep V or Hα frames was not removed, and (3) any feature which displayed a ‘soft’ core (suggesting a non-stellar profile) was not removed. Operationally, there is no simple method to automatically apply the above criteria, so we allowed the processing pipeline remove objects beyond the 5% isophote, but used visual inspection for the inner regions.

The results are fairly successful as can be seen in Figure 2. The bottom images are the cleaned and filled frames for V and Spitzer 3.6 μm. There is very little obvious evidence of the removed areas, and there is no disjoint increase or decrease in the aperture magnitudes curve-of-growth that would signal an error in the filled regions. However, at 3.6 μm, these corrections involve a significant fraction of the galaxy light, up to 15%, and make comparison with other studies difficult. This technique is much more conservative than the methods applied by Muñoz-Mateos et al. (2009), for a comparison of their cleaned images (their Figure 2) indicates a number of faint point sources that remain after cleaning. As their SINGS (Spitzer Infrared Nearby Galaxies Survey) sample studies HSB spirals and irregulars, their slightly lower luminosities should not significantly contribute to their error budget, but may be critical in our LSB sample.

2.4 Isophotometry

Determining mean isophotes followed the same procedures that we have applied to optical data for LSB galaxies (Schombert et al. 2011). Frames that were manually cleaned were submitted to the ARCHANGEL pipeline (Schombert 2007) in the same manner as optical data. Sky boxes were used to determine the local sky in each frame. Ellipse fitting was performed using the standard Fourier series iterative least-squares algorithm. Given the irregular morphology of LSB galaxies, very few of the isophote contours are truly elliptical. However, to first order, a round shape with a long and short axis is the best approximation and the errors in the surface photometry are dominated by knowledge of the sky value rather than RMS around each ellipse. All the data (images, surface brightness profiles, colours, and fit parameters) are found at our website, http://abyss.uoregon.edu/~js/spitzer.

A few selected surface brightness profiles are shown in Figure 3 to display the range in the sample in terms of size and central surface brightness. The surface brightness profiles for the entire sample are available for download from our website. While some LSB galaxies have a clear bulge and disk appearance (plus a double-horned HI profile), which signals a rotational dominate oblate 3D shape, many LSB galaxies are irregular in appearance (some with single-horned HI profiles) with no indication that they are oblate, prolate or triaxial in 3D shape (Sung et al. 1998). However, historically, LSB surface brightness profiles are displayed as the major axis (r) versus surface brightness (μ, mag arcsecs⁻²) and fit with exponential fitting functions assuming a flattened shape. We simply follow past procedure, but make the reader aware that this does not assume a disk-like structure for all LSB galaxies (Schombert et al. 1997).

Figure 3. A comparison of four surface brightness profiles in V (blue) and 3.6 μm (red). The resulting V − 3.6 colour profiles are also shown. The depth of the 3.6-μm data is compatible to the optical data, and all the features in the optical profiles are reproduced in the 3.6-μm profiles despite the broad range in morphology.

Aperture and total magnitudes are determined from the same procedures as the optical data for LSB galaxies (Schombert, McGaugh, & Maciel 2013). Aperture magnitudes used the best fit ellipses for the radius in question. Luminosities were summed for all the unmasked pixels interior to the ellipse (a surveyor method was used to include the partial pixels at the ellipse edge). Masked pixels were replaced with the mean surface brightness of the fitted isophote for that radius. The amount of galaxy light derived from masked pixels varied from 2% to 15%. Total magnitudes were derived from asymptotic fits to the curve-of-growth. Beyond the 90% total luminosity radius, the apertures were replaced by the mean isophote value in order to capture the light associated with the very LSB halos.

This adjusted curve-of-growth procedure is highly successful for the LSB galaxies in the sample as all the galaxies have well-defined curves of growth at the faint ends that convert to clear total magnitudes. The errors quoted in Tables 3 and 4 reflect the Poisson noise for the galaxies, error in the sky value, and errors in the asymptotic fit. Of the three sources of error, Poisson noise dominates the total magnitude calculations by a factor of 10. While the errors are atypically low, comparison with other studies will reveal differences due to luminosity determination techniques rather than an external check to the luminosities. For example, comparison with SING luminosities (Muñoz-Mateos et al. 2011) reveals an external scatter of 5% to 10%.

Galaxy size is determined by the isophotal Holmberg radius (Holmberg 1958; Faber & Gallagher 1979). This is the size of the major axis at the point where the surface brightness profile reaches 26.5 B mag arcsecs⁻². Assuming a B − V colour of 0.5 and a V − 3.6 colour of 2.5 produces a surface brightness cutoff of 23.5 mag arcsecs⁻² at 3.6 μm. However, using this isophote only captures 50% to 60% of an LSB galaxies light (due to colour gradients). Therefore, we reduced the isophote value to 24.5, which captures typically 80% of a galaxy's light. This isophote is used to calculate the Holmberg radii ( $R_{\text{H}}$ ) quoted in Tables 3 and 4, the major axis of the galaxy at the 24.5 3.6-μm isophote. As displayed in Figure 1, the galaxy sizes in the sample range from dwarfs (1 to 2 kpcs) to large disks (10 to 20 kpcs). The Holmberg radius is strongly correlated with disk scale length (α, based on exponential fits to the profile) such that 2.5α is equivalent to a galaxy's Holmberg radius.

Comparison to optical colours used either Johnson V frames obtained from the KPNO 2.1m (Schombert et al. 2011) or SDSS (Sloan Digital Sky Survey) g frames taken from DR7 (seventh data release; Abazajian et al. 2009). The SDSS g values were converted to Johnson V using the standard SDSS conversions (Jester et al. 2005). Colours (V/g − 3.6 μm) were calculated by three methods: (1) direct subtraction of the aperture magnitudes (integrated colours), (2) differences in the surface brightness V and 3.6 μm profiles, and (3) differential magnitudes (annular apertures). Of the three methods, the best total colours were provided by direct comparison of the asymptotic magnitudes. The best measure of spatial colour was the differential surface brightness profiles, examples of which are shown in Figure 3. Colour gradients were determined using interpolation of the surface brightness profiles. Again, the errors were dominated by sky value in both V and 3.6 μm and were added in quadrature for the errors on the quoted colours.

3 DISCUSSION

3.1 Optical to mid-IR surface brightness profiles

The most important result from our study is that the Spitzer observations reach to similar depth and radii as the deepest optical surface brightness profiles, in many cases farther than previous optical work of similar exposure times. This type of accuracy in the IR is simply not obtainable from the ground due to the high atmospheric absorption combined with a bright background. Therefore, IR space imaging has numerous advantages for studies of galaxy mass since a mid-IR luminosity minimises the internal absorption corrections, resulting in photometric parameters that better reflect the underlying stellar population (McGaugh & Schombert 2013). In addition, the morphology and structure of a galaxy in the mid-IR will tend to follow the underlying kinematic stellar distribution, rather than being distorted by dust lanes and recent star formation.

The visual morphology of the LSB galaxies falls, primarily, into the extreme late-type classes (Sm, Im or dI). Only two of the dwarf LSB galaxies (D-class) have any symmetric shape (Sm class) and only seven of the F-class LSB galaxies have Sc or Sd morphology. The appearance of all the LSB galaxies at 3.6 μm is identical to their optical appearance (see Figure 2). This was not unexpected as optical colour maps reveal very little absorption by dust or gas, so extinction that changes the morphology of early-type spirals from optical to IR has little effect on LSB galaxies. This also reinforces expectations that, with low SFRs, LSB galaxies will vary little in stellar population age with spatial position, unlike spirals.

Surface brightness profiles are found in Figure 3, and visual inspection of the side-by-side surface brightness profiles reveals that the optical and mid-IR profiles follow the same slopes and contain the same general features (bulges, lens, and disk length). The few differences in the optical and mid-IR profiles can be attributed to asymmetric features (i.e., star-forming regions, see Section 3.1) which can have different luminosities at the optical and IR wavelengths depending on the age of the stellar population. This result was also expected based on the behavior of multi-wavelength profiles from the SINGS project (Muñoz-Mateos et al. 2009, see their Figure 6) where strong differences in profile shape were noted between the near-UV and far-IR, but with little change from optical to the mid-IR.

It is standard procedure to fit late-type galaxies to exponential profiles, for one the most distinguishing characteristics between ellipticals and spirals is a power-law versus exponential surface brightness profile (Schombert & Smith 2012). The consistency of these shapes as a function of morphology suggests that this is a property that is imposed during galaxy formation and tied to physical properties, such as total angular momentum. With respect to disk galaxies, exponential profiles in the outer regions are well defined by two parameters, central surface brightness (μ _o ) and scale length (α; van der Kruit 2002). Central surface brightness is only loosely correlated with global galaxies properties, such as galaxy mass. However, scale length, which is independent of Hubble type, increases with galaxy mass (de Jong 1996; Fathi 2010).

The fitting of an exponential profile to an irregular galaxy often has subtle differences compared to procedures for spirals. Very few of the LSB galaxies in our sample have a well-defined bulge+disk appearance (e.g., F568-1, in Figure 2, F579-1, and UGC 11557). Of the 59 galaxies in the sample classified as LSB, only 15 have canonical bulge+disk morphology, although this is not a statement on the morphology of LSB galaxies as a type of galaxy as all the D-class galaxies in our sample were selected for irregular morphology and specifically avoiding a disk-like appearance. Without a well-defined bulge, the location of the isophotal centre becomes an exercise of the region of highest surface brightness or the geometric mean from outer isophotes.

While symmetric disk galaxies are not dominant in our sample, even an irregular LSB galaxy tends to have a brighter central region surrounded by a fainter envelope. This central region is rarely at the same centre as the outer isophotes, but is typically within a half of a scale length (α) of the mean isophotal centre. Truly undefined objects (e.g., D500-4, F565-V2, UGC 5209) are rare, as are galaxies with nearly constant interior surface brightness than a sharp drop-off (box profile, e.g., D500-3, D572-5, ESO215-G009).

Despite their irregularities, most of the surface brightness profiles at 3.6 μm are adequately described by an exponential fit. We divided the sample by profile shape in three categories: (1) box-like shape (flat core region with an exponential drop-off), (2) disk (pure exponential), and (3) bulge+disk (two distinct components, the bulge need not be a r ^1/4 power-law shape as is common with bright spiral bulges). These classifications are listed in Tables 1 and 2. Half the LSB samples have profiles which are described by a single exponential (disk-like), which due to the close correspondence to the optical profiles, matches previous results (Schombert et al. 2013). The other half of the sample was evenly divided into box-like and bulge+disk shapes. Unsurprisingly, the box-like profiles are associated with most irregular morphologies and the least elliptical isophotal shape.

We have also classified each profile according to the classification scheme proposed by Erwin et al. (2008), where a Type I profile has no breaks from an exponential, Type II has a downward break, and Type III has an upbending break. Only nine (15%) galaxies were classed as Type II or III, which is significantly different from Herrmann, Hunter, & Elmegreen (2013) who found 77% of their dwarfs to have Type II or III profiles. For our dwarf galaxies (R ₂₅<10 kpc) our Type II or III numbers increase to 30% of the sample. Part of the difference is due to stylistic differences in applying the classification scheme. For example, a box-like profile would automatically be a Type II profile, however, if the flattened profile is clearly an interior phenomenon and unrelated to the exponential fit in the halo, we called this a Type I. Part of the difference is also due to the LSB nature of our sample, as the outer isophotes have less S/N than higher surface brightness systems. Larger error bars would disguise any break.

Figure 4 displays a comparison of scale length, α, obtained by exponential fits to the 48 galaxies in our sample with both optical (V or SDSS g) and mid-IR (3.6-μm) profiles. The correspondence is excellent considering the differences in wavelength, telescopes, detectors, and sky background. The total radial extent of the stellar component of a LSB galaxy is well described either by optical or near-IR imaging. However, space mid-IR imaging displays greater S/N due to the fact that the luminosity of older stars peaks in the mid-IR and the sky is darker than the ground. There is a slight tendency for large galaxies to be under-sized at 3.6 μm and small galaxies to be over-sized (compared to their V scale lengths), but the trend is not statistically strong.

Figure 4. Comparison of size and luminosity between optical and mid-IR imaging. The top panel display a comparison of scalelength, α, based on exponential fits where the blue line is the unity relationship. Given the similarity between the optical and mid-IR surface brightness profiles, the close correspondence between scalelength fits is unsurprising and reinforces the universality of the exponential shape for late-type galaxies. The comparison of total apparent magnitude is shown in the bottom panel, the unity line assumes a V − 3.6 colour of 2.3. The correspondence is excellent considering the range in colour for LSB galaxies.

We conclude that the exponential profile shape for LSB galaxies is universal at 3.6 μm, even given the problematics due to irregular isophotes. There is no compelling reason to conclude any other fitting function is a better fit, particularly considering the uniformity in profiles from optical V to the mid-IR. Given the range in kinematics for the sample, from rotating disk with flat rotation curves to triaxial irregulars with solid-body motion, the mechanism determining galaxy structure must be ubiquitous. Also, given the similarity in shape between HSB and LSB galaxies, star formation must not play a dominant role (Ferguson & Clarke 2001). Simulations of gravitationally self-consistent disk collapse naturally produce exponential shapes (Mestel 1963; Dalcanton, Spergel, & Summers 1997), however, the exact mechanism is unclear. Features such as bars and spiral arms serve to redistribute angular momentum (Hohl 1971) and tend to form double exponentials as seen by Herrmann et al. (2013). But these features are rare in LSB galaxies (which may explain the lack of double exponentials in our sample).

The most likely mechanism is the one proposed by Elmegreen & Struck (2013), where stellar scattering off of baryon clumps (stars or gas) leads to the formation of exponential profiles. In their simulations, a sufficiently strong irregular morphology, which very much describes an LSB sample, drives a uniform and cold disk into an exponential shape. For objects in our sample, where most of the baryons are located in distinct regions, the timescale for an exponential formation is less than a gigayear. Their simulations also indicate that asymmetric features tend to be permanent, which explains why the internal colours in LSB galaxies are so uniform between the lower and higher surface brightness regions, indicating the stellar populations across an LSB disk have evolved in lockstep with the surface brightness of the feature (Schombert et al. 2013).

3.2 Optical to mid-IR luminosities/colours

Also shown in Figure 4 is a comparison of total magnitudes in V (or g) and 3.6 μm. Again the correspondence is excellent (a mean V − 3.6 colour of 2.3 is assumed for the unity line), and the lack of a broader scatter is a statement concerning the low range in V − 3.6 colour for late-type galaxies. LSB galaxies display better uniformity in colour at 3.6 μm than the optical bandpasses. Converting 3.6 μm to stellar mass (McGaugh & Schombert 2013) gives a range of 10⁷ to 10¹⁰ M _⊙ for LSB galaxies with a mean of 10⁹ M _⊙ versus the HSB galaxies in the sample with a mean of 5×10¹⁰ M _⊙. These value are consistent with optically derived masses.

Mean V − 3.6 colours are shown in Figure 5 for both the LSB and HSB galaxies in the sample with both optical and mid-IR imaging. These are isophotal colours, rather than aperture colours, meaning they are weighted by number of pixels rather than luminosity of the pixels. This produces a total colour that underweights bulge and core regions, and emphasises the colour of the LSB regions. Despite the different methods, the isophotal colours never differed from the total aperture colours by more than 0.3 mags.

Figure 5. Histogram of the total V − 3.6 colours for the LSB and HSB galaxies in our sample. A mean colour of 2.3 with a standard deviation of 0.5 is measured for the sample.

The mean V − 3.6 colour for the sample was 2.3, excluding the HSB galaxies from the average. As can be seen from Figure 5, the HSB galaxies are 1.5 mags redder than the LSB galaxies although we note that the LSB sample has a mean absolute magnitude of −19 and the HSB galaxies have a mean of −24, meaning that some of this colour difference could be due to the mass-metallicity effect. However, the SFR is higher in HSB galaxies which should offset any metallicity effects.

The canonical test of the mass-metallicity effect is the colour-magnitude relation (CMR; Tully, Mould & Aaronson 1982; Peletier & de Grijs 1998). Although the CMR is clearer for early-type galaxies (whose lack of current star formation produces a relationship dominated solely by metallicity effects), the CMR for spirals and irregulars is also a useful stellar population diagnostic. For example, regardless of the dominant processes (star formation or chemical evolution), comparison of the CMR in spirals and irregulars between clusters and the fields illuminates environmental processes (Mobasher, Ellis, & Sharples 1986).

The CMR for our sample is shown in the top panel of Figure 6. The various symbols represent our sample, the THINGS (The HI Nearby Galaxy Survey) data (Leroy et al. 2008), and the sample from Dale et al. (2005), all of which cover a range of luminosities and Hubble types. The red line is the CMR for ellipticals, which is pure mass-metallicity. No corrections are made for internal extinction. While dust is minimal in LSB galaxies, some of the scatter in the THINGS and Dale datasets are due to the lack of extinction corrections. Colour gradients are also quite strong in spiral galaxies (see Section 3.3), so this effect will also contribute to the large scatter around a linear best fit.

Figure 6. The top panel displays the colour-magnitude relation (CMR) for our sample (black symbols, solid for LSB, open for HSB) and the Dale et al. (2005) sample of early-type spirals (blue). The relationship for ellipticals and S0's (Falcón-Barroso et al. 2011) is denoted by the red line, the blue line is the fit to spiral galaxies from Peletier & de Grijs (1998) corrected to V − 3.6 using a mean colours of K − 3.6 = 0.3. The steeper slope, compared to ellipticals, indicates that star formation/age is an increasingly dominant component to the CMR over pure metallicity effects. The bottom panel displays the relationship between Hα luminosity (i.e., current SFR) and stellar mass (absolute 3.6-μm luminosity).

Despite the large scatter, the correlation between colour and luminosity is clear in Figure 6. Brighter galaxies tend to be earlier in Hubble type, thus, the relationship converges onto the elliptical sequence as the bulge light dominates a galaxy's colour. However, the slope is much steeper than the elliptical/S0 sequence, therefore metallicity cannot be the sole component to the late-type CMR (at least, not global metallicity set by the onset of galactic winds). Stellar mass (using M _3.6 as a proxy) is also strongly correlated with Hα luminosity (a proxy for the SFR, see bottom panel of Figure 6). However, the relationship between SFR and colour is inverse to the expected bluer colours with more star formation.

The solution appears to be a combination of the explanations proposed by Tully et al. (1982) and Peletier and de Grijs (1998). First, the spiral CMR is due, in part, to an increase in the ratio of young to old stellar populations for later-type galaxies. Evolution from a star-forming spiral to an S0 (by mass) must begin with an abrupt cessation of star formation to jump from the spiral CMR to the elliptical/S0 CMR (crossing the ‘green valley’; Strateva et al. 2001). The analysis by Peletier and de Grijs (1998) shows that decreasing mean age is insufficient to explain the spiral CMR slope, and an additional metallicity component is required. This agrees well with the studies of [OIII] lines in dwarf galaxies (Zahid et al. 2012) and large colour surveys with SDSS (Tojeiro et al. 2013) where galaxies of the same morphology have their colours correlated with SFR, not mass.

Further illumination to the underlying stellar population in LSB galaxies is given by the two-colour B − V versus V − 3.6 diagram, shown in Figure 7. The red symbols are early-type galaxies from Falcón-Barroso et al. (2011), the blue symbols are the LSB galaxies from our sample. Also shown are single-burst 12- and 3-Gyrs multi-metallicity models (Rakos & Schombert 2009) where the red side of the models represents [Fe/H] = +0.3 and the blue side represents [Fe/H] = −0.5. A majority of ellipticals are well described by a single age of 12 Gyrs with the variation in colour due to the mass-metallicity effect. S0- and Sa-type galaxies have slightly younger mean ages, but none are bluer than the 3-Gyrs model.

Figure 7. The two-colour diagram, B − V versus V − 3.6, for the LSB galaxies in our sample with both optical and mid-IR photometry. The red symbols are early-type galaxies from Falcón-Barroso et al. (2011), and blue symbols are LSB galaxies. The two solid lines are 12- and 3-Gyrs multi-metallicity burst models from Schombert & Rakos (2009) based on Bruzual & Charlot (2003) isochrones. The grid represents models of constant star formation over 12 Gyrs with varying terminal [Fe/H] values. Bluer and redder models are constructed by assuming a four-fold increase/decrease in star formation over the last 0.5 Gyrs.

Star-forming galaxies (late-type) display much bluer optical and mid-IR colours, and a much larger range in V − 3.6 colour. The range of colour are incompatible with any single age or frosting model (where an old population contains a small fraction of young stars; Schombert & McGaugh 2013). We note that the current SFR of LSB galaxies, divided by their stellar mass, is near a Hubble time (Schombert et al. 2013). This implies that the mean SFR in LSB galaxies has been nearly constant for their lifetimes. While this rate may vary wildly at any particular epoch, a first-order stellar population model is one which assumes a constant SFR, then sums the luminosities over all the generations to form a final colour. It is this type of model that is shown in Figure 7.

The constant star formation model shown in Figure 7 is based on modified Bruzual & Charlot SSP's (single stellar populations, single age, and metallicity isochrones). The BC03 models were successfully modified to reproduce the CMR for ellipticals using a multi-metallicity technique (Odell, Schombert, & Rakos 2002). Multi-metallicity populations are generated by selecting BC03 models of a single age and summing various metallicities using the shape of the metallicity distribution in our Galaxy, and allowing the peak to vary to represent a changing mean [Fe/H]. To model a constant star formation population, the total population is divided into a number of bins from 12 Gyrs to the present. Each age is assigned a mean [Fe/H] starting at [Fe/H]= − 1.7 at 12 Gyrs and advanced to a final value that varied from −1.5 to +0.3 following a chemical evolution prescription (Prantzos 2009) and following the CMR with redshift (Zahid et al. 2013). Each bin is summed to and weighted by the mean luminosity compared to the 12-Gyr bin (i.e., older, more metal-poor stars tend to be brighter than their younger, metal-rich counterparts).

In addition, as our data covers the mid-IR portion, we extended the BC03 models to cover TP-AGB evolutionary tracks (Marigo et al. 2008). This correction begins for populations older than 40 Myrs with a Δ(V − 3.6) = 0.5, dropping to 0.2 by 500 Myrs and less than 0.05 for greater than 2 Gyrs. While this correction is applied to each age bin, the total effect is Δ(V − 3.6) = 0.25 with respect to models without the AGB correction. This is a significant difference in Figure 7 resulting in primarily overestimating an LSB galaxy's metallicity. We have ignored extinction effects due to the low dust content in LSB galaxies (these models are described in greater detail in Schombert & McGaugh 2013).

The mid line in Figure 7 presents the final model with a run of mean galaxy metallicity from <Fe/H > = −1.5 to solar. Due to the stochastic nature of star formation, we also considered two other models where the star formation was suppressed by a factor of four for the last 0.5 Gyrs and where the star formation was enhanced by a factor of four for the last 0.5 Gyrs (4× and 1/4×). The resulting model tracks are shown in Figure 7 where changing the recent star formation has the largest effect in B − V colour as expected.

A majority of the LSB colours fall within the range of models described above. The mean colour for the sample falls exactly on the midline model, although the colour errors prevent any exact mapping of star formation history to a particular galaxy. We can rule out a majority of the stars in LSB galaxies being formed in the last few gigayears, or their V − 3.6 colours would be much redder due to a strong TP-AGB component. The spread in colours are well matched by the models with enhanced/suppressed SFR by factors of four, which is consistent with the spread in Hα emission as a function of stellar mass for LSB galaxies (Schombert et al. 2013).

3.3 Colour gradients

Colour gradients between V (or g) and 3.6 μm are found at the bottom of each surface brightness plot. These are calculated by interpolating the 3.6-μm surface brightness value at each V surface brightness point. The resulting colour gradients are shown in Figure 8 where the colour profiles have be normalised to r = 1 kpc and divided into two groups: (1) those with flat or slightly rising profiles, and (2) those with decreasing colours with radius. The sample divides evenly into those galaxies with flat versus decreasing colour gradients. The mean down gradient is Δ(V − 3.6)/log R = −0.4, the mean up gradient is Δ(V − 3.6)/log R = +0.3.

Figure 8. The V − 3.6 colour gradients for 45 LSB galaxies. The gradients are normalised to r = 1 kpc. Flat or rising gradients are shown in the top panel, downward gradients are displayed in the bottom panel. The sample is evenly divided into flat/upward versus downward gradients. LSB galaxies with late-type morphology or low baryon mass tend to have flat or upward gradients.

Galaxies with decreasing gradients are predominately disk-like in morphology. Those galaxies with flat gradients are irregular in morphology or dwarf-like. Galaxies with decreasing gradients are brighter, on average, than flat or increasing-gradient galaxies, but both types are found at all masses. There is a sharp transition with respect to baryon mass. A majority of the galaxies with baryon masses less than 10⁹ M _⊙ have flat or upward colour gradients, those galaxies with masses greater than 10⁹ M _⊙ have downward gradients. This is similar to the result found by Tortora et al. (2010) for 50 000 SDSS galaxies.

While colour gradients in early-type galaxies are primarily due to metallicity effects, disk- and late-type galaxies have significant star formation which could produce a colour gradient based on mean local stellar age. Since the CMR for our sample is significantly steeper than the slope of the CMR for ellipticals, star formation must play a strong role in the observed colour gradients herein. In addition, those galaxies with downward gradients have, on average, 100 times more Hα emission than flat gradient galaxies in our sample. Flat gradients for low-mass LSB galaxies probably reflect their already low-mean metallicities, due to a suppressed past SFR, such that there is very little dynamic range in [Fe/H] within the entire galaxy.

All the galaxies with up or flat gradients have no gradients in B − V. And a majority of the galaxies with downward gradients also have no or very modest B − V gradients. The lack of optical gradients is a known property of LSB galaxies (Schombert et al. 2013), mostly due to the fact that star formation is more dispersed in LSB galaxies compared to their HSB cousins. This implies that the LSB gradients are dominated by metallicity effects, rather than age (recent SF, see Figure 7) and the low SFR in LSB galaxies may allow a sharper analysis of metallicity gradients (i.e., spatial chemical evolution) due to decoupling of SF effects.

4 SUMMARY

Deep Spitzer surface photometry is presented for 61 LSB galaxies (45 with matching optical imaging) and an additional 14 HSB galaxies. Spitzer imaging has several unique data reduction challenges, such as a sharp increase in the number of background point sources, all of which can be resolved with well-designed software routines. The data presented herein have comparable depth to sky-limited optical imaging, but at wavelengths that are impossible to achieve from the ground and measure the portion of a galaxy's spectral energy distribution (SED) critical to estimates of galaxy stellar mass and star formation history. Our results are summarised as the following:

1. (1) Our sample, selected for low central surface brightness (μ _o <19 mag arcsecs⁻² at 3.6 μm), covers a luminosity range of −11 to −22 in M _3.6, a size range of 1 to 25 kpc, and gas mass fraction of 30% to 95%. While a majority of the sample is gas-rich (f_g >0.5), the only defining characteristic to the sample is central surface brightness, not mass or size.

2. (2) Surface brightness profiles at 3.6 μm have identical features to profiles at V, regardless of galaxy morphology. Contrary to studies of HSB dwarfs (Herrmann et al. 2013), we find a majority of LSB galaxies have single exponential profiles with only 15% displaying upward or downward breaks from a single exponential. Part of this difference may be due to the lower S/N in LSB envelopes, which disguises outer changes in the profile shape.

3. (3) V − 3.6 colours of LSB galaxies are bluer than their HSB counterparts with a mean colour of 2.3 and a standard deviation of 0.5. The CMR is evident for LSB galaxies, with a similar slope to that found for normal spirals, indicating that star formation (age) dominates over metallicity effects.

4. (4) The timescale for total star formation in LSB galaxies (M _*/SFR, the ratio of the total stellar mass to the current SFR) is near a Hubble time implying a history of constant, albeit extremely low, star formation. This is consistent with the fact that single-age stellar population models (where all the stars are of a single age, but varying metallicities) fail to reproduce the blue optical colours compared with red near-IR colours (a signature of a mixed-age stellar population). However, the mean LSB optical to mid-IR colours do compare well with models of constant star formation, as can be seen in Figure 7.

5. (5) The spread in B − V colour for LSB galaxies can be modelled by assuming a fourfold decrease/increase in star formation over the last 0.5 Gyrs. These quasi-stochastic bursts of star formation would explain the weak correlation between SFR and surface brightness (Paper I, where low SFR is associated with low-stellar-density galaxies) such that the wide variation in SFR versus surface brightness is due to the present SFR being a snapshot of the current epoch and the mean surface brightness represents the integrated effect of star formation over the age of the galaxy.

6. (6) Downward colour gradients exist for 1/2 the sample, but low-mass and late-type-morphology LSB galaxies display no gradients. Gradients appear to be driven more by metallicity effects as irregular LSB galaxies have very low SFR and are relatively uniform in disk colour.

Our sample emphasises the promise that mid-IR imaging has for studies attempting to measure the total luminosity and size of a galaxy population, particularly with respect to formation correlations such as the TF relation and the Fundamental Plane. More surprising is the information provided by optical to mid-IR colours with respect to the underlying stellar population. The combination of near-IR colours with current SFRs from Hα imaging yields a clearer picture of star formation in LSB galaxies than afforded by optical colours alone. The model of roughly constant mean star formation rate punctuated by stochastic variations in current SFR agrees well with constraints from kinematic studies, providing a natural explanation for the observed range of stellar mass-to-light ratios. We will use these as inputs towards a coherent history of the evolution of LSB galaxies in the next paper of our series.