Photometric Variability of the mCP Star CS Vir: Evolution of the Rotation Period

Abstract

The aim of this study is to accurately calculate the rotational period of CS Vir by using STEREO observations and investigate a possible period variation of the star with the help of all accessible data. The STEREO data that cover 5-yr time interval between 2007 and 2011 are analysed by means of the Lomb–Scargle and Phase Dispersion Minimization methods. In order to obtain a reliable rotation period and its error value, computational algorithms such as the Levenberg–Marquardt and Monte Carlo simulation algorithms are applied to the data sets. Thus, the rotation period of CS Vir is improved to be 9.29572(12) d by using the 5-yr of combined data set. Also, the light elements are calculated as HJD_max = 2454715.975(11) + 9^d_· 29572(12) × E + 9^d_· 78(1.13) × 10 ^{− 8} × E² by means of the extremum times derived from the STEREO light curves and archives. Moreover, with this study, a period variation is revealed for the first time, and it is found that the period has lengthened by 0.66(8) s y⁻¹, equivalent to 66 s per century. Additionally, a time-scale for a possible spin-down is calculated around τ_SD ~ 10⁶ yr. The differential rotation and magnetic braking are thought to be responsible of the mentioned rotational deceleration. It is deduced that the spin-down time-scale of the star is nearly three orders of magnitude shorter than its main-sequence lifetime (τ_MS ~ 10⁹ yr). It is, in return, suggested that the process of increase in the period might be reversible.

1 INTRODUCTION: CHEMICALLY PECULIAR STARS

Chemically Peculiar (CP) stars are located from the zero age main sequence (MS) to the terminal age MS. They have masses in the range between 1.5 M_⊙ and about 7 M_⊙ (Netopil et al. 2014), and their spectral types spread from early-B to late-F (Smith 1996). Therefore, they contain stars with effective temperatures greater than 6 500 K (Hubrig et al. 2005). In general, CP stars consist of A and B type peculiar (Ap and Bp, respectively) variables separated from normal stars which have the same effective temperature due to their abnormal chemical compositions and low rotational velocities (typically vsini < 120 km s⁻¹; Abt 2000). The reasons of this peculiarity are the under-abundance of solar-like elements as well as over-abundance of metal and rare-earth elements seen in these stars (Mikulášek et al. 2009).

Based on their chemical peculiarity, CP variables are divided into four main subgroups as CP1, CP2, CP3, and CP4 (Preston 1974). Also, they are clearly split up into two main groups by the fact that CP2 and some of the CP4 stars show organised magnetic fields with a large-scale structure (typically from 300 G to about 30 kG), whereas CP1 and CP3 stars do not have such magnetic fields (Preston 1974). Although the production mechanism of these magnetic fields is still a matter of debate, the fossil field theory is the most widely accepted mechanism which successfully explains the above mentioned field formation in Ap and Bp stars (LeBlanc 2010).

The formation of anomalous chemical compositions is another controversial issue for CP stars. Several hypotheses such as the interior nucleosynthesis resulting from evolution (Fowler et al. 1965), surface contamination of a normal star by a supernova companion (Guthrie 1967), radiative diffusion by gravity and radiation pressure (Michaud 1970), and the selective accretion of interstellar matter via the stellar magnetic field (Havnes & Conti 1971) have been proposed. However, none of these theories, except the radiative diffusion—which leads to the accumulation or depreciation of the atoms at certain depths and causes some of the elements to become excessive at the surface—can successfully account for the CP phenomenon (Michaud 2004).

Magnetic fields also play an important role in the distributions of elements at the stellar surface by directly affecting radiative acceleration and atomic diffusion. Such that the spherical symmetry of the diffusive segregation of chemical elements is broken due to the Zeeman splitting and the Lorentz force. So, the diffusions that take place in the presence of horizontal and vertical magnetic fields differ from each other. This situation is thought to cause the formation of spots and rings of enhanced element abundance (Michaud, Charland, & Megessier 1981).

With the combination of the stellar rotation, these non-uniformly distributed spot regions on the surface cause periodic variations in the average magnetic field characteristics, line profiles, spectral energy distribution, and brightness in different photometric bands (Kochukhov 2011), and all of these variations can best be explained by the oblique-rotator model (Stibbs 1950).

From several observations, it is known that the phases of these periodic modulations are directly correlated (Catalano, Kroll, & Leone 1992). For some CP stars, the phase extrema of the variations coincide with each other (53 Cam; Jarzȩbowski 1960), while some of the extrema occur in the anti-phase for some other stars (CS Vir; Mikulášek et al. 2004). On the other hand, in some cases such as HD 83 368 (Polosukhina et al. 1999), the extrema do not take place at the same time even though the periods of all these variations are same.

Most of the CP stars are slow rotators with periods roughly between a day and a week. Long-term observations have revealed that the geometry of the spots can remain stable on the surface for decades as a consequence of the slow rotation. Thereupon, surface distribution, rotational periods, and even rotational braking of some of these stars can be calculated with unprecedented accuracies (Mikulášek et al. 2008; Kochukhov 2011).

Although a vast majority of the discovered CP stars do not exhibit a light curve or a period variation, it is reported that there is a small number of them such as SX Ari ( $\dot{P}=0.02$ s y⁻¹; Adelman et al. 2001), V901 Ori ( $\dot{P} = 0.356$ s y⁻¹; Mikulášek et al. 2014), and CU Vir ( $\dot{P}= 0.165$ s y⁻¹; Pyper, Stevens, & Adelman 2013) whose rotation periods slightly or excessively change over decades, and it is thought that magnetic braking is the major cause of these variations.

The changes in period can be easily obtained through long-term monitoring of seasonal light curves. However, peculiarities of only a small fraction of CP have been investigated, and approximately one-tenth of these stars have been considered in terms of rotation or photometric periods. To determine these parameters, high-precision instruments and long-term observations are needed (with an accuracy better than 0.005 mag; Mikulášek et al. 2009).

In order to present the light variations and the evolution of rotational period of magnetic CP (mCP) star CS Vir, this paper is organised as follows: in Section 2, the literature studies of the star are reviewed; in Section 3, the STEREO satellite is briefly introduced; in Section 4, the characteristics of the photometric data and the pipeline used for light curve analyses are described. In Section 5, the results on CS Vir are presented, and finally the overall study is summarised and the results are discussed in Section 6.

2 LITERATURE REVIEW OF CS VIR

CS Vir (HD 125 248; HIP 69 929; HR 5355) (A9SrEuCr, V = 5.86 mag) is a well-known, bright mCP star that has attracted the attention of many researchers due to its line strength and light curve variabilities for several decades (Table 1).

Table 1. Available period values for CS Vir. The periods, except the last four values, are around a mean value of 9.2954 d. The last four data excessively deviate from the mean value and do not fit the STEREO light curves very well.

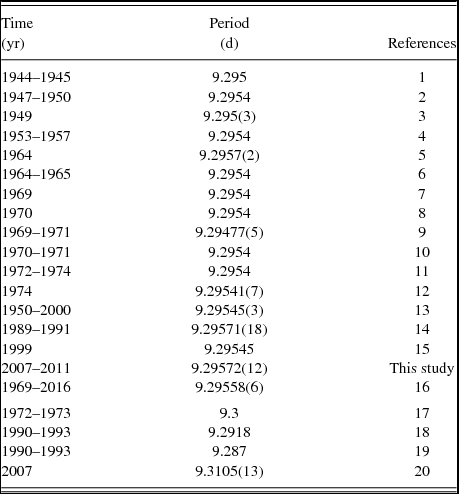
References. (1) Deutsch (1947); (2) Babcock (1951); (3) Stibbs (1950); (4) Babcock (1960); (5) Adam (1965); (6) Hockey (1969); (7) Maitzen & Rakosch (1970); (8) Wolff & Wolff (1971); (9) Blanco, Catalano, & Strazzulla (1978); (10) Maitzen & Moffat (1972); (11) Pyper & Adelman (1985); (12) Renson (1975); (13) Mikulášek et al. (2004); (14) Catalano et al. (1992); (15) Leone & Catanzaro (2001); (16) Rusomarov et al. (2016); (17) Pilachowski & Bonsack (1975); (18) Dubath et al. (2011); (19) Perryman et al. (1997); (20) Wraight et al. (2012).

Morgan (1931) was the first investigator who detected variable line intensities similar to those in α² CVn. Deutsch (1947) confirmed non-harmonic intensity variation and found that Eu II and Cr II lines changed in the same period (~9.295 d), but in opposite phases (the maximum of Eu II modulation coincided with the minimum of Cr II).

Stibbs (1950) photoelectrically obtained the light curve of the star with a period of 9.295 d (A = 0.053 mag), and found that the phase of the light maximum with respect to the Eu II variation was 0.55, but coincided with the maximum of Cr II variation. They also proposed the oblique rotator model for the first time in order to explain the photometric, spectral, and magnetic field variations.

Babcock (1951) studied on the magnetic variability of CS Vir and explored a large reversing magnetic field with a variation period of around 9.3 d. They observed that the Eu II maximum occurred when magnetic polarity reached the positive maximum. Based on the variabilities in the observations, they stated that the star was a component of a binary system.

The spectroscopic observations by Hockey (1969) verified that the star was a spectroscopic binary with the period of 4.4 yrs. On the basis of magnetic field observations, they showed that the rotational period of CS Vir was 9.2954 d. Unlike other studies, Blanco et al. (1978) found a slightly shorter period of 9.29477 d after 3 yrs observation, and reported that the light variation in V-band was double-waved whereas U- and B-bands showed single-wave curves.

Contrary to the arguments that Ap magnetic stars do not have a large inhomogeneities of oxygen, Mathys (1992) revealed that the atmosphere of CS Vir exhibited a strong and large inhomogeneous oxygen distribution. Additionally, Catalano et al. (1992) observed some variabilities in infra-red region and derived the best period to be 9.29571(18) d, compatible with visible light, spectrum, and magnetic field variations.

Mikulášek et al. (2004) improved the rotational period of star as 9.295450(30) d by combining 592 observations over 43 yrs. Finally, Rusomarov et al. (2016) obtained high-resolution spectropolarimetric observations of CS Vir to have a better understanding of the mechanism of atomic diffusion in the presence of magnetic fields. They constructed detailed maps of the surface magnetic field and abundance distributions for the star and showed that its magnetic field has mostly been poloidal and quasi-dipolar with two large spots of different polarity and field strength. Combining 47 yrs of longitudinal field measurements with their own observations, they improved the rotational period of the star to be P _rot = 9.29558(6) d.

3 THE SOLAR TERRESTRIAL RELATIONS OBSERVATORY

The Solar TErrestrial RElations Observatory, STEREO, is the third mission of the ‘Solar Terrestrial Probes’ programme of the NASA. Two identically designed spacecrafts are positioned in a heliocentric orbit at radii of ~1 au. STEREO-A (orbiting ahead of the Earth) and STEREO-B (orbiting behind the Earth) orbit around the Sun while they drift away from the Earth in opposite directions.

STEREO monitors coronal mass ejections of the Sun and their propagations in the interplanetary medium. For this task, the satellites have been equipped with several instrument packages. The Sun Earth Connection Coronal and Heliospheric Investigation (SECCHI) is one of these packages and includes the Heliospheric Imagers (HI), which contain two visible-light cameras (HI-1 and HI-2), referred to HI-1A, HI-1B, HI-2A, and HI-2B, depending on the satellite on which they are located. They produce photometric data by pointing near to the solar disk and monitoring brightness of background stars around the ecliptic (V = 12 mag or brighter). The HI-1 instrument observes the stars in 20° by 20° field of view (FOV) with 40 min cadence for ~20 d, while HI-2 has a 70° by 70° FOV and 2-h cadence. For details of the HI instruments, refer to Eyles et al. (2009) and Bewsher et al. (2010).

As periods of most mCP stars vary from several hours to days, STEREO satellite is quite suitable to detect these periodic signals. Also, spectral energy distribution of mCP stars decreases with increasing wavelengths in visual spectral range. Since the spectral response of the HI instruments is very broad (400 nm up to 950 nm), the window around 400 nm in the filter allows STEREO to be sensitive to the variations of mCP stars (Mikulášek 2007).

For this study, only the data from HI-1A are used since the data from the other three instruments are progressively deteriorating. A more detailed description of the basic light curves can be found in Sangaralingam & Stevens (2011) and Whittaker, Stevens, & Sangaralingam (2013).

4 PHOTOMETRIC DATA AND LIGHT CURVE ANALYSIS

Seasonal data comprise an observation interval of ~20 d. The cadence of the data is a photometry point every 40 min. This data set allows to perform analysis in a wide frequency range with the Nyquist frequency of around 18 c d⁻¹ (~1.5 h).

In order to analyse the data of CS Vir, the light curves are needed to be decontaminated from internal and external effects caused by the circumstances mentioned by Sangaralingam & Stevens (2011). Therefore, long-term variations are removed from the light curves by using a third-order polynomial fit, which is the CCD response function of HI-1A, and observation points greater than 3σ are clipped. Thus, the light curves cleaned from spurious effects are obtained.

The light curve of CS Vir has presented a sinusoidal characteristic due to a spot modulation on stellar surface. All analyses are therefore performed using the Lomb-Scargle (LS) algorithm since this method is sensitive to such variations (Lomb 1976; Scargle 1982). During the analyses, the number of independent frequencies (N _id) is calculated by employing N _raw/2, where N _raw is the number of observation points in the raw data (e.g. N _id = 325 for light curve of CS Vir taken in 2007). Also, false alarm probability (FAP) is assumed to be 99% (P ₀ = 0.01). Apart from these, signals are sought between the frequency range of 0.05–18 c d⁻¹, and variabilities greater than the Nyquist frequency are not taken into account.

The Levenberg–Marquardt Optimisation (LM-fit) Method is applied to the curve by defining a simple Fourier series to determine a model of the examined sinusoidal light curve. Moreover, more than one Fourier series with different coefficients and their derivatives are defined in the case of any other harmonics in the light curve. Frequency and amplitude values derived from the LS analysis of the cleaned light curve are used as initial parameters. As a result of 5 000 iterations, the most accurate fit with the smallest error value is obtained.

Once a model light curve is derived, the most accurate frequency and its uncertainty are assessed using the Monte Carlo simulation algorithm. To do this, random Gaussian noise with the mean of zero and the sigma value determined from the cleaned curve is produced and the noise component is then added to the model fit. Subsequently, another LS procedure is implemented to this noisy curve. Once a frequency value is identified, all these processes are repeated by adding another noise component to the model curve. After 500 repetitions, 500 random frequencies are produced around the actual frequency. When a probability distribution is performed by a histogram, a well-defined peak, close to the expected value, is plotted on the diagram, and the most accurate frequency is calculated using a simple Gaussian fit (Figure 1). Moreover, the final frequency error is found from the standard deviation of these 500 frequencies.

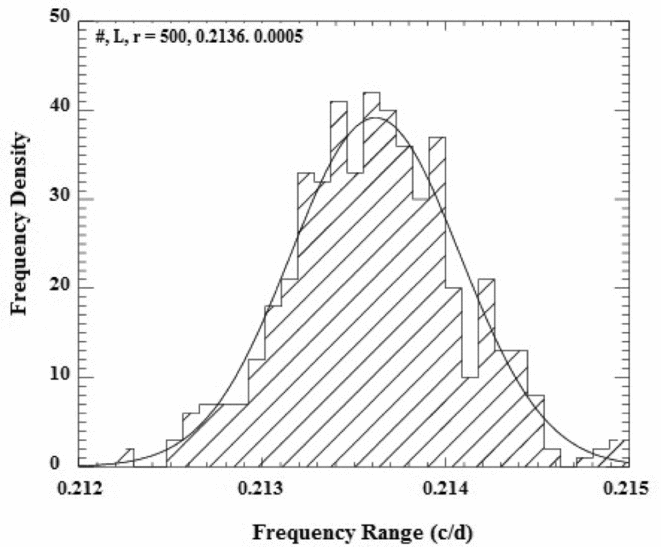
Figure 1. Frequency probability distribution of the data taken in 2007 and the best Gaussian fit made to calculate the most accurate frequency. #, L, and r denote the number of random frequencies used for histogram, frequency of cycles in a day, and its error derived from the Gaussian fit, respectively.

All processes taking part in the analyses are repeated by using the Phase Dispersion Minimization (PDM) technique to make a comparison with LS frequencies. The results are also compared with the period values given in the literature and with data derived by the Hipparcos satellite. Phased light curve profile of the star is generated based on periods derived from combination of all seasonal light curves.

The maximum times are obtained from the seasonal light curves by means of the Kwee–van Woerden method (Kwee & van Woerden 1956) to investigate period variability over years, and those with the smallest errors are put together with data from the literature (Table 2). In the first column of the Table 2, the archival extremum times (Raw Extremum Times) are given as Julian Date (JD). The star symbols in this column indicate that these data have been interpolated either from line intensity measurements or photometric data sets. Also, the obelisk symbols (†) in the same column represent minimum times derived either from the light curves or from line intensities at ϕ = 0.5. These data have been subjected to phase correction for shifting to zero phase. Phase corrected extremum times have been converted to Heliocentric JD and are presented in the fourth column of the Table 2. The archival data with no standard deviation are marked with the asterisk symbols (⋆). The error values of these data are assumed to be ±0.1 d.

Table 2. All available extremum times for CS Vir. In the first column, the archival time values (Raw Extremum Times) are given as Julian Date (JD). The star symbols indicate that these data have been interpolated from archival data sets. The obelisk symbols represent minimum times derived either from the light curves or from line intensities. Phase corrected extremum times, which have also been converted to Heliocentric JD, are presented in the fourth column. The archival data with no standard deviation value are marked with the asterisk symbols. The error values of these data are assumed to be ±0.1 d. Last two columns are the epoch and O–C values calculated from the maximum times.

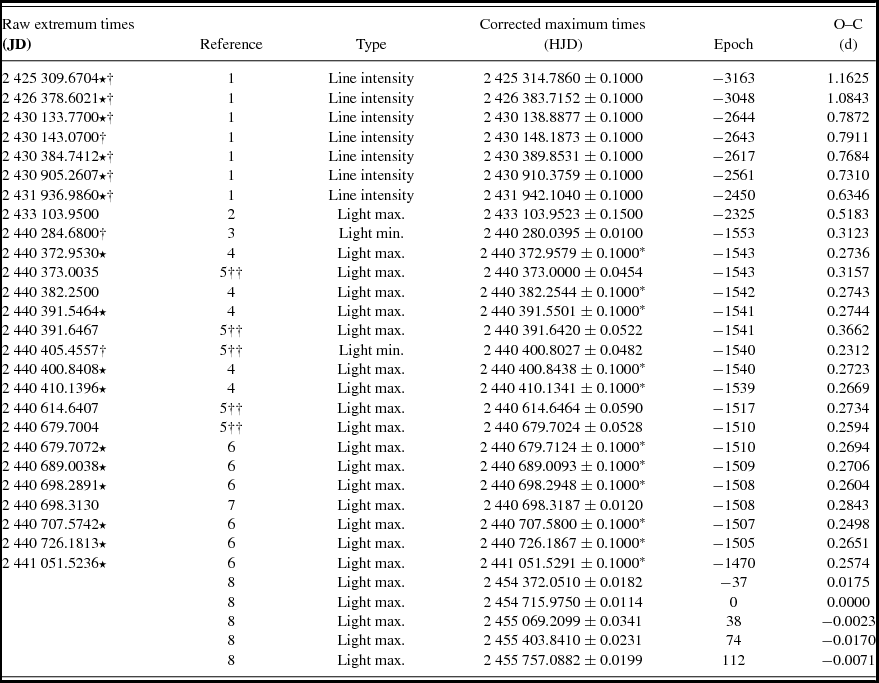
Notes. †† http://astro.physics.muni.cz/mcpod/ References. (1) Deutsch (1947); (2) Stibbs (1950); (3) Blanco et al. (1978); (4) Maitzen & Rakosch (1970); (5) mCPod; (6) Maitzen & Moffat (1972); (7) Mikulášek et al. (2004); (8) STEREO (this study).

The times of photometric maximum light of the star are presented in the form of

$$\begin{equation*} HJD_\mathrm{max} = T_\mathrm{0} + PE + \frac{1}{2}\frac{\text{d}P}{\text{d}t} \overline{P}E^2, \end{equation*}$$

where T ₀ is the zero epoch, P is the rotational period in days, E is the number of cycles and $\frac{1}{2}\frac{\text{d}P}{\text{d}t} \overline{P}$ represents the long-term variation in period.

5 RESULTS

In this study, 5-yr light curves of CS Vir taken between 2007 and 2011 are analysed, and the details related to the data are given in Table 3. Due to some satellite-related problems, such as pointing discontinuity or tracking error, the numbers of seasonal raw data are less than 720 points (the maximum number of observation points taken in 20 d). Except the light curve data taken in 2009, the curves consist of ~600 data points. Even though the data sets do not have the maximum number of observation points, the sinusoidal structure of the light curve is clearly observed as shown in Figure 2.

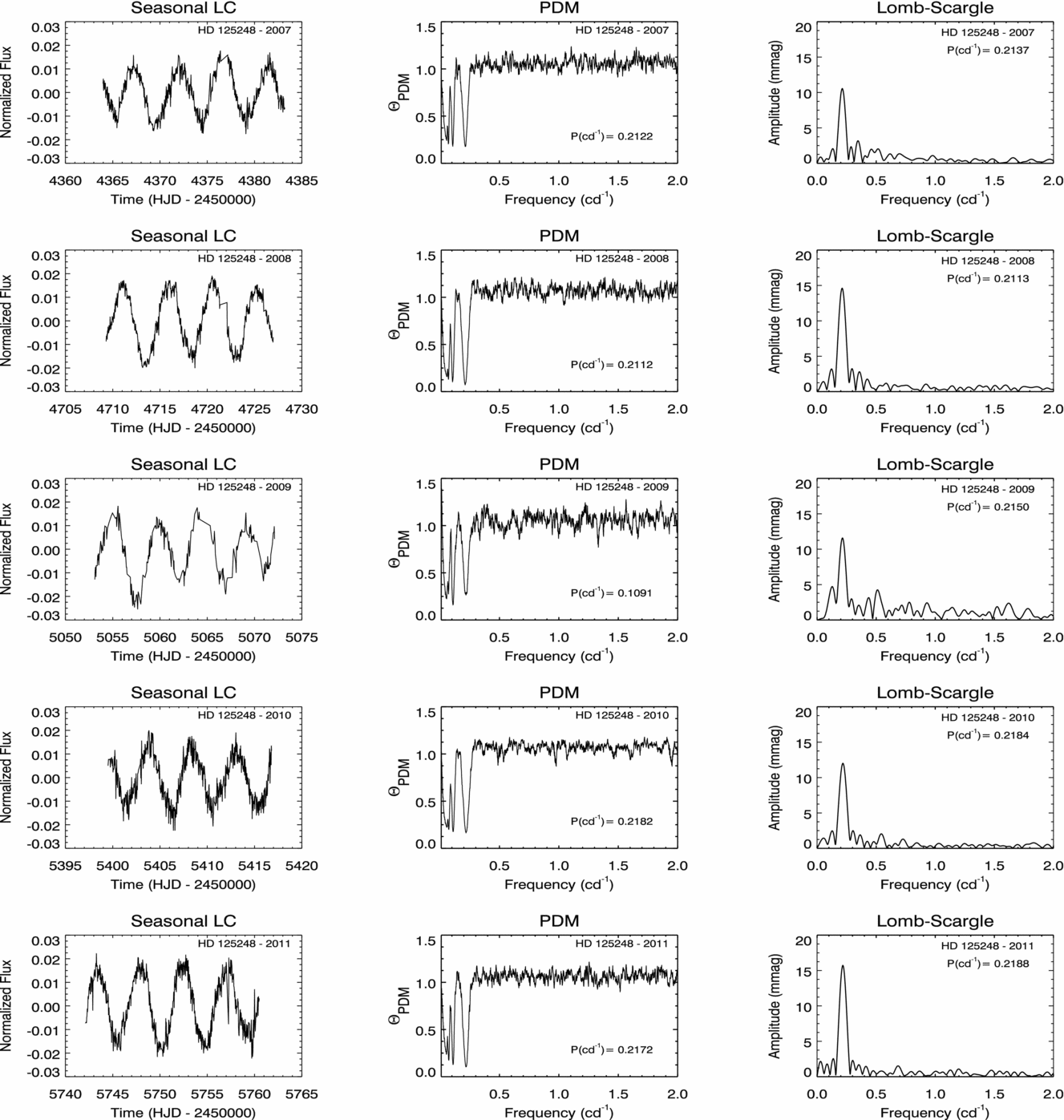
Figure 2. Annual light curves, related PDM and LS analyses of CS Vir are shown in the columns. In the first column, the x-axis of the light curves represents the observation duration in Heliocentric JD and the y-axis shows normalised flux count calculated from ( $F(t)/\overline{F}) -1$ .

Table 3. Details of the seasonal and combined observations of CS Vir. Observation years, observation lengths, start, and mid times of each observation, the numbers of raw and cleaned data points, frequencies and amplitudes derived from the seasonal and combined data sets with the Lomb–Scargle method are given in the table. Due to some satellite-related problems, such as pointing discontinuity or tracking error, the numbers of seasonal raw data points are less than 720 points (maximum points derived in 20 d).

For the analyses, the LS method is initially applied to the seasonal data and a period value of around 4.64 d, half of the literature period, is acquired for each year. Following this, each data set is analysed by using the PDM technique. As the number of light cycles is limited, the PDM method also detects a period of ~ 4.60 d for the seasonal data sets (except for 2009). On the other hand, the frequency analyses of the 5-yr combined data show that the actual period is around 9.29 d. Therefore, the seasonal periods are assumed to be the twice of the LS and PDM results.

The LS and PDM periods of the 5-yr data combination are used to check general light curve characteristics of CS Vir. Since the LS period (0.107576(1) c d⁻¹) provides a more suitable folded curve having the less scattered data points and the smallest sigma value, it is chosen for the further calculations. As shown in Figure 3 (upper left), the main light curve exhibits a double-waved structure that is not observed in most studies discussed in Section 2. In this plot, it is seen that one of the maxima is slightly shallower than the other. Moreover, the analysis of the Hipparcos data produces a similar period (0.10763 c d⁻¹) to that of the STEREO (Figure 3, upper right).

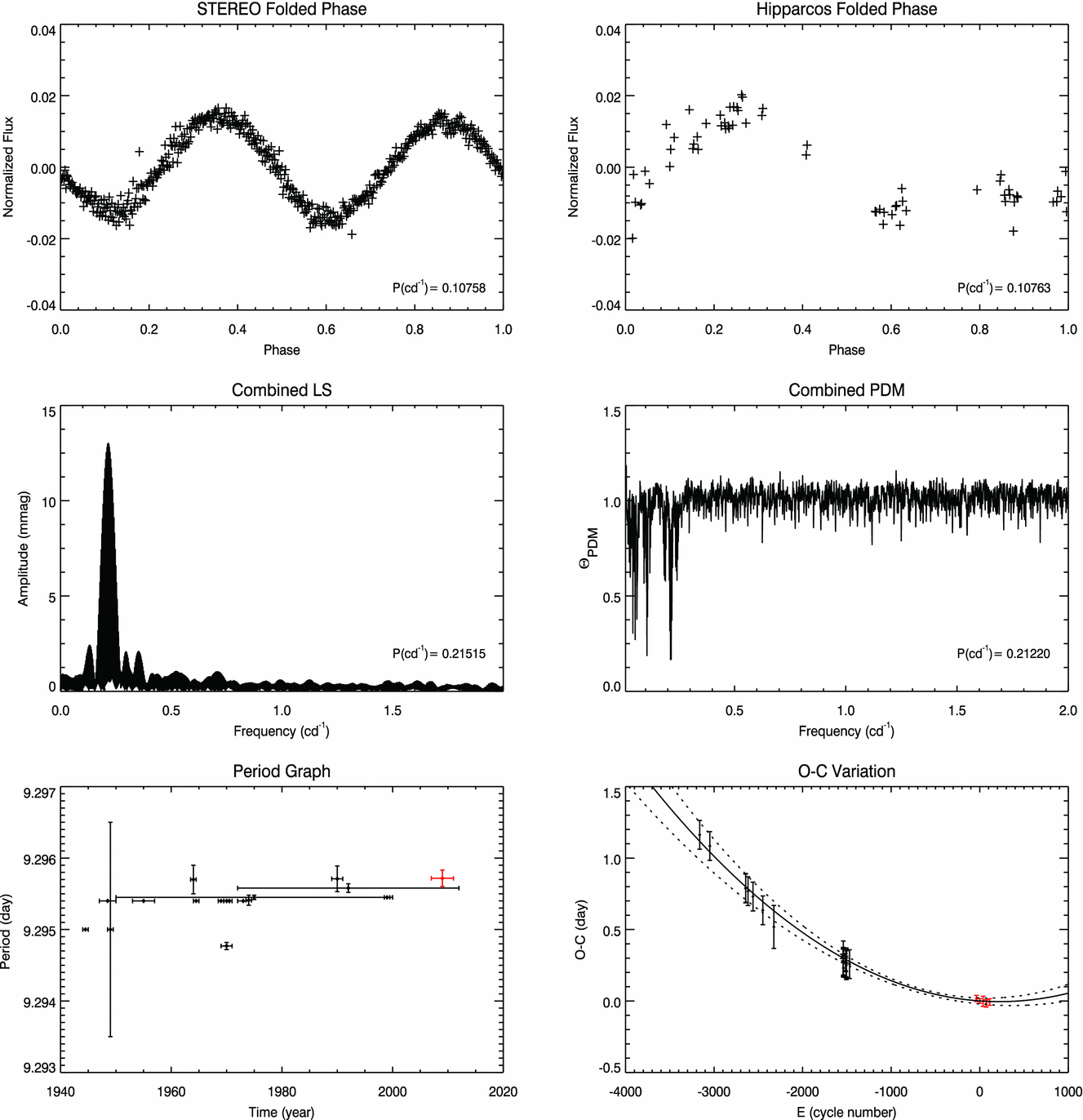
Figure 3. Analysis results of CS Vir. Folded light curves produced by the STEREO and the Hipparcos periods are given in the first row. The phase folded light curves do not have the same shape since the Hipparcos observations have been performed using Hp filter (ESA 1997). A sample Hp observation of the star can be also seen in Mikulášek et al. (2004). LS and PDM analyses of the combined light curve are presented in the second row. Period and O–C variation graphs of CS Vir are shown in the last row. The long-term rotational change in the observed time of the light maximum minus the calculated time of light maximum is expressed in days.

Thereto, a possible long-term period variation is investigated by collecting all available archival data, even though a stable period is reported by several authors. More than 20 periods have been given in archives as seen in Table 1. The majority of these values are around a mean period of 9.2954 d, whereas the last four data in the table excessively deviates from this value and do not fit the STEREO light curves very well. Therefore, they have not been used for our calculations. In Figure 3 (left bottom), archival and combined STEREO period values are shown with black and red diamond symbols, respectively. From the graph, it is not easy to deduce any period change in the star, because the vast majority of the data are gathered around the mean value. However, our 5-yr combined data suggest a moderate increase in the period if it is assessed with the result from Rusomarov et al. (2016).

For the purpose of substantiating this period change, E and O–C values are determined from the maximum times given in the Table 2 and presented in the last two columns of the same table. Data, covering a long time interval, come from different observers using various detectors and different pass bands. Such data are not homogeneous and their effects in the O–C diagram should be appropriately evaluated. Therefore, the errors of the O–C values are calculated by using the error propagation method. Accordingly, all errors from the maximum times T, reference maximum time T ₀ and period P are considered even if the uncertainties of T ₀ and P do not significantly affect the result. On the other hand, based on Sterken (2005), the cycle number E is assumed to be error-free since it has been a function of T. Together with the errors, O–C values are shown in Figure 3 (right bottom). As seen from the figure, the data display a parabolic variation, which opens upward, since 1930. To calculate the rate of this parabolic change, O–C values are fitted with the Levenberg–Marquardt least-squares method, which iteratively minimises the sum of the squares of the errors between the data points and the function through a sequence of updates to parameter values. The solid and dashed lines in the figure are the best fit to the data and the 1-σ uncertainty from the fit, respectively. As a result of this fitting procedure, the period variation is found to be around 0.66(8) s y⁻¹, or 66(8) s per century.

Based on these results, the times of maximum light of the star are computed as HJD _max = 2454715.975(11) + 9^d _· 29572(12) × E + 9^d _· 78(1.13) × 10 ^{− 8} × E ².

6 DISCUSSION AND SUMMARY

In this study, photometric data of CS Vir are derived from STEREO satellite between 2007 and 2011 to investigate its period evolution. During the analyses, 5 yrs of seasonal light curves and a compilation of these data are examined with one of the most widely used frequency detection methods, LS. By cleaning the light curves from the distorted effects, the best periods are obtained with a precision of 10⁻⁴ and 10⁻⁶ c d⁻¹ for the seasonal and combined data sets, respectively. These are then used to investigate a possible variation in period. From the STEREO light curves, the seasonal maximum times with the smallest error values are calculated and supplemented with all the relevant archived observations that are available to study the period evolution seen in the O–C diagram.

Based on the examination of the STEREO and archival data, it is detected that CS Vir has an explicit period variation in its O–C diagram. The data collected since 1930 indicated that the period has been gradually increasing over years. Accordingly, the rotation of CS Vir has slowed down by 0.66(8) s per year. Such a deceleration in rotation suggests a possible decrease in the kinetic energy of the star. Using the physical parameters given in Table 4, the energy and the rate at which the energy decreased are roughly calculated as E = 1.02(19) × 10⁴⁵ erg and dE/dt = −5.33(1.17) × 10³¹ erg s⁻¹. According to its period variation, the spin-down time-scale of the star is approximately τ_SD = 1.21(35) × 10⁶ yr. The MS lifetime of the star is also found as τ_MS = 1.29(9) × 10⁹ yr from the equation of τ_MS = 10¹⁰ yr × (M/M_⊙)^{(1 − α)}, where α = 3.5 for MS stars and 10¹⁰ yr is the approximate lifetime of the Sun in the MS (Ghosh 2007; Koupelis & Kuhn 2007; Hansen & Kawaler 1994).

Table 4. Physical parameters of CS Vir. temperature, luminosity, and mass values have been adopted from Kochukhov & Bagnulo (2006). Radius and rotational velocities were estimated from period, temperature, and luminosity values.

Table 5. Period and its variation rate as well as spin-down and main sequence lifetime of CS Vir.

As stated by several researchers such as Mikulášek et al. (2009), strict periodicity due to slow rotation is a common property of the majority of CP stars. However, it is reported in the literature that a small number of CP stars shows notable period changes within several years. CU Vir ( $\dot{P}/P = 5.28 \times 10^{-14}$ s⁻¹) and V901 Ori ( $\dot{P}/P = 1.33 \times 10^{-13}$ s⁻¹), which have sinusoidal period variations, as well as BS Cir, which has a moderate rotation deceleration ( $\dot{P}/P = 3.02 \times 10^{-14}$ s⁻¹), are some of the most important samples among these type of stars (Mikulášek et al. 2014).

In relation to these period variations, Meynet & Maeder (2006) suggest that the moment of inertia and rotation period should change in mildly rotating stars showing no substantial angular momentum loss, and that evolution models in fact predict a slow down in their stellar rotation. Mikulášek et al. (2014) point out that the fastest change in period is seen in the most massive stars (τ_MS ≈ 30 M yr), and is roughly $\dot{P}/P = 1.04 \times 10^{-15}$ s⁻¹. However, change rates given for CU Vir, V901 Ori, and BS Cir are several times greater than evolutionary changes. From the findings in this study, such a result is also confirmed. The variation in period of CS Vir ( $\dot{P}/P \sim 10^{-14}$ s⁻¹) is 10 times greater than that of the most massive CP stars ( $\dot{P}/P \sim 10^{-15}$ s⁻¹) discussed by Mikulášek et al. (2014), and also quite compatible with their findings. In addition, the spin-down time-scale of the star is found around τ_MS ~ 10⁶ yr (Table 5). This value is nearly three orders of magnitude shorter than the MS lifetime of the star (τ_MS = 10⁹ yr). This, in turn, suggests that the process of the increase in the period of CS Vir might be reversible. If so, the length of these cycles could be roughly estimated to be 248(14) yr for CS Vir.

It is not possible to measure rotational deceleration caused by stellar evolution of MS stars with current methods, since variation rates are quite small. Also, if rotational evolution is a consequence only of evolutionary changes, the rotational periods of CP stars would be relatively constant (Mikulášek et al. 2014). In spite of this, observational facts indicate that the periods of some CPs vary. As a result, numerous hypotheses related to the origin of these changes have been offered. These hypotheses, all of which assume that these stars rotate as a solid body (Stibbs 1950), can be outlined as (1) mass and radius variations during MS evolution, (2) angular momentum loss because of standard and magnetised stellar winds, (3) precession of rotation axis, (4) light-time effect occurring due to an additional component.

The reason for the period decrease in CP stars can be explained by the first item given above. However, it has been already mentioned that detection of rotational slowing due to evolutionary reasons is not possible since variation is at least three times larger than the observational limits. Also, the spin-down time-scale caused by the standard stellar winds cannot be measured, because it is much larger than the evolutionary time-scale (Mikulášek et al. 2014). For the third explanation, the effects of precession in rotation axis should be seen as cyclic changes in light curves. Yet, there is no peculiarity observed in the STEREO light curves of CS Vir, and no archival records have been found related to such changes. Also, Mikulášek et al. (2014) indicate that the amplitude of these variations originating from precession can be ignored. Finally, the last mechanism is a light-time effect, which causes a cyclic variations in the O–C diagram. Even though it has been reported that the star is a spectroscopic binary, this case is also not appropriate as its O–C variation shows a parabolic change.

On the other hand, this parabolic O–C diagram may be indicating a mass transfer existing between the components. If such a situation is indeed in question, the increment in the period should be the result of a mass transfer occurring towards the more massive component from the less massive one. When the semi-amplitude of the radial velocity variation (K = 7.60(17) km s⁻¹) and the orbital period (P _orb = 1618(8.1) d) are adopted from Abt & Snowden (1973), and sin³ i is assumed to be 0.679 (Hogeveen 1992), the mass of the companion star is estimated to be around 1.0 M_⊙. According to this, the radii of the Roche Lobes of the components are calculated as RL ₁ = 123 R_⊙ and RL ₂ = 87 R_⊙ by using the formula given by Eggleton (1983), and this result reveals that there is no mass transfer in this system yet.

Considering the options outlined above and the fact that period variation process might be reversible due to shorter spin-down time-scale than that of MS lifetime, the rigid rotation hypothesis should be discarded and the differential rotation model should alternatively be discussed in detail as expressed by Stepien (1998). As a result of such a rotation, an interaction between the layers takes place and hence, a cyclic increase and decrease in the moment of inertia occurs (Stepien 1998). This means that an unexpected alternating variability of rotation periods can be observed. In this case, rotation deceleration in CS Vir may be interpreted as a consequence of torsional oscillations produced by meridional circulations being in interaction with a magnetic field, and of rotational braking in outer layers caused by angular momentum loss via magnetically confined stellar wind. Such explanation, which the angular momentum loss that occurs due to magnetic winds can be calculated for the hot CP stars with strong magnetic fields, is also supported by Mikulášek et al. (2014).

There are numerous compiled catalogues with hundreds of CP stars, including Paunzen et al. (2013) and Wraight et al. (2012) (STEREO), Niemczura, Morel, & Aerts (2009) (CoRoT), and Romanyuk & Kudryavtsev (2008) (ground-based). There are also several studies related to surface structures (CoRoT stars HD 49 310 and HD 50 773; Paunzen et al. 2015; Lüftinger et al. 2010), and pulsational behaviour of CP stars (CoRoT object HD 45 975; Morel et al. 2014). However, few studies have been performed to achieve a better understanding of the period changes of these variables (Mikulášek et al. 2010, 2014, etc.), and almost none of them are based on space-based missions. Therefore, this investigation is quite important in terms of contributing to the studies on the period evolution of CP stars.

To increase the accuracy and precision of the results, the amount of data collected between 2007 and 2011 can be increased. For this purpose, the data of the HI-1A obtained after 2011 can be collected, or light curves observed by the HI-1B and the HI-2 can be made compatible with HI-1A data. Additionally, the FOVs of SMEI and K2 overlap the HI-1 image. Thus, if there is any available data provided by these missions, the current data can be combined with them. As a result, further information about the evolutionary stage of CS Vir can be obtained.