1. Introduction
Cosmic reionisation, a pivotal epoch in the history of the Universe, marks the last phase transition of the Universe when neutral hydrogen (H i) in the intergalactic medium (IGM) became fully ionised, ending the cosmic ‘Dark Ages.’ However, the precise timing of reionisation and sources capable of emitting sufficient ionising photons remain subjects of active debate till date. Previously, it was believed that reionisation was largely complete by
![]() $z\sim 6$
(Fan et al. Reference Fan2006). However, recent studies suggest a relatively late end of reionisation at
$z\sim 6$
(Fan et al. Reference Fan2006). However, recent studies suggest a relatively late end of reionisation at
![]() $z\sim 5.3 - 5.5$
(Becker et al. Reference Becker2015; Kulkarni et al. Reference Kulkarni2019; Cain et al. Reference Cain, D’Aloisio, Gangolli and Becker2021; Bosman et al. Reference Bosman2022). A common belief is that galaxies which are faint in intrinsic ultraviolet (UV) radiation are the primary contributors of reionisation, typically releasing about 10 % of their Lyman continuum (LyC) photons (see Finkelstein et al. Reference Finkelstein2019; Dayal et al. Reference Dayal2020). However, to explain the relatively rapid decrease in the neutral IGM fraction in later epochs, it is possible that more infrequent luminous sources might also have played a significant role (see Naidu et al. Reference Naidu2020).
$z\sim 5.3 - 5.5$
(Becker et al. Reference Becker2015; Kulkarni et al. Reference Kulkarni2019; Cain et al. Reference Cain, D’Aloisio, Gangolli and Becker2021; Bosman et al. Reference Bosman2022). A common belief is that galaxies which are faint in intrinsic ultraviolet (UV) radiation are the primary contributors of reionisation, typically releasing about 10 % of their Lyman continuum (LyC) photons (see Finkelstein et al. Reference Finkelstein2019; Dayal et al. Reference Dayal2020). However, to explain the relatively rapid decrease in the neutral IGM fraction in later epochs, it is possible that more infrequent luminous sources might also have played a significant role (see Naidu et al. Reference Naidu2020).
Due to the attenuation of UV photons below the Lyman break by the increasingly neutral IGM at
![]() $z \gt 4$
(e.g. Inoue et al. Reference Inoue, Shimizu, Iwata and Tanaka2014; Steidel et al. Reference Steidel2018), direct observation of LyC photons is almost impossible. Reionisation models suggest that a minimum escape fraction of LyC photons,
$z \gt 4$
(e.g. Inoue et al. Reference Inoue, Shimizu, Iwata and Tanaka2014; Steidel et al. Reference Steidel2018), direct observation of LyC photons is almost impossible. Reionisation models suggest that a minimum escape fraction of LyC photons,
![]() $f^{\mathrm{LyC}}_{\mathrm{esc}} \gtrsim 10$
% is required to complete reionisation (Robertson et al. Reference Robertson, Ellis, Furlanetto and Dunlop2015; Finkelstein et al. Reference Finkelstein2019). Therefore, it is crucial to comprehend how LyC photons escape into the IGM and subsequently ionise it during the epoch of reionisation (EoR). Several studies have attempted to make connection between
$f^{\mathrm{LyC}}_{\mathrm{esc}} \gtrsim 10$
% is required to complete reionisation (Robertson et al. Reference Robertson, Ellis, Furlanetto and Dunlop2015; Finkelstein et al. Reference Finkelstein2019). Therefore, it is crucial to comprehend how LyC photons escape into the IGM and subsequently ionise it during the epoch of reionisation (EoR). Several studies have attempted to make connection between
![]() $f^{\mathrm{LyC}}_{\mathrm{esc}}$
and nebular emission line features such as [O iii], C iv, C iii Mg ii etc (see, Izotov et al. Reference Izotov2020; Nakajima et al. Reference Nakajima, Ellis, Robertson, Tang and Stark2020; Schaerer et al. Reference Schaerer2022; Katz et al. Reference Katz2022; Xu et al. Reference Xu2022; Mascia et al. Reference Mascia2023; Choustikov et al. Reference Choustikov2024).
$f^{\mathrm{LyC}}_{\mathrm{esc}}$
and nebular emission line features such as [O iii], C iv, C iii Mg ii etc (see, Izotov et al. Reference Izotov2020; Nakajima et al. Reference Nakajima, Ellis, Robertson, Tang and Stark2020; Schaerer et al. Reference Schaerer2022; Katz et al. Reference Katz2022; Xu et al. Reference Xu2022; Mascia et al. Reference Mascia2023; Choustikov et al. Reference Choustikov2024).
The Ly
![]() $\alpha$
emission line of atomic hydrogen has been identified as the most reliable indirect tracer of LyC leakage and is used as one of the promising probes of the EoR (Kakiichi et al. Reference Kakiichi, Dijkstra, Ciardi and Graziani2016; Laursen et al. Reference Laursen, Sommer-Larsen, Milvang-Jensen, Fynbo and Razoumov2019; Tang et al. Reference Tang2023). A rapid decline in the fraction of Ly
$\alpha$
emission line of atomic hydrogen has been identified as the most reliable indirect tracer of LyC leakage and is used as one of the promising probes of the EoR (Kakiichi et al. Reference Kakiichi, Dijkstra, Ciardi and Graziani2016; Laursen et al. Reference Laursen, Sommer-Larsen, Milvang-Jensen, Fynbo and Razoumov2019; Tang et al. Reference Tang2023). A rapid decline in the fraction of Ly
![]() $\alpha$
emitting galaxies (LAEs) towards higher redshifts (
$\alpha$
emitting galaxies (LAEs) towards higher redshifts (
![]() $z \gt 5$
) has been interpreted as a rapid escalation in the H i fraction with increasing redshift (Pentericci et al. Reference Pentericci2011; Tilvi et al. Reference Tilvi2014; Stark et al. Reference Stark2017; Hoag et al. Reference Hoag2019; Whitler et al. Reference Whitler2020; Jones et al. Reference Jones2024; Nakane et al. Reference Nakane2024; Napolitano et al. Reference Napolitano2024; Tang et al. Reference Tang, Stark, Topping, Mason and Ellis2024a). Both the observed intensity and shape of the Ly
$z \gt 5$
) has been interpreted as a rapid escalation in the H i fraction with increasing redshift (Pentericci et al. Reference Pentericci2011; Tilvi et al. Reference Tilvi2014; Stark et al. Reference Stark2017; Hoag et al. Reference Hoag2019; Whitler et al. Reference Whitler2020; Jones et al. Reference Jones2024; Nakane et al. Reference Nakane2024; Napolitano et al. Reference Napolitano2024; Tang et al. Reference Tang, Stark, Topping, Mason and Ellis2024a). Both the observed intensity and shape of the Ly
![]() $\alpha$
line offer delicate insights into the proportion of H i within the IGM (Robertson et al. Reference Robertson, Ellis, Dunlop, McLure and Stark2010). The Ly
$\alpha$
line offer delicate insights into the proportion of H i within the IGM (Robertson et al. Reference Robertson, Ellis, Dunlop, McLure and Stark2010). The Ly
![]() $\alpha$
rest-frame equivalent width (
$\alpha$
rest-frame equivalent width (
![]() $\mathrm{EW}_0$
) has been identified as an excellent indicator of Ly
$\mathrm{EW}_0$
) has been identified as an excellent indicator of Ly
![]() $\alpha$
escape fraction (
$\alpha$
escape fraction (
![]() $f^{\mathrm{Ly}\alpha}_{\mathrm{esc}}$
; see Matthee et al. Reference Matthee2017b; Begley et al. Reference Begley2024; Tang et al. Reference Tang2024b). The separation between the blue and red peaks in the double-peak emission can be used to infer H i column densities (
$f^{\mathrm{Ly}\alpha}_{\mathrm{esc}}$
; see Matthee et al. Reference Matthee2017b; Begley et al. Reference Begley2024; Tang et al. Reference Tang2024b). The separation between the blue and red peaks in the double-peak emission can be used to infer H i column densities (
![]() $N_{\mathrm{HI}}$
), consequently, the escape of LyC photons (see, Verhamme et al. Reference Verhamme, Orlitová, Schaerer and Hayes2015; Verhamme et al. Reference Verhamme2017; Izotov et al. Reference Izotov2018; Naidu et al. Reference Naidu2022). Furthermore, the detection of a stronger blue-peak profile also indicates a very low column density channel of H i that can leak LyC photons (see, Furtak et al. Reference Furtak2022; Mukherjee et al. Reference Mukherjee2023). However, the blue-peak is expected to be scattered away by the neutral IGM at
$N_{\mathrm{HI}}$
), consequently, the escape of LyC photons (see, Verhamme et al. Reference Verhamme, Orlitová, Schaerer and Hayes2015; Verhamme et al. Reference Verhamme2017; Izotov et al. Reference Izotov2018; Naidu et al. Reference Naidu2022). Furthermore, the detection of a stronger blue-peak profile also indicates a very low column density channel of H i that can leak LyC photons (see, Furtak et al. Reference Furtak2022; Mukherjee et al. Reference Mukherjee2023). However, the blue-peak is expected to be scattered away by the neutral IGM at
![]() $z \gt 5$
(Hu et al. Reference Hu2010; Hayes et al. Reference Hayes, Runnholm, Gronke and Scarlata2021), leaving only a single-peak red-skewed profile.
$z \gt 5$
(Hu et al. Reference Hu2010; Hayes et al. Reference Hayes, Runnholm, Gronke and Scarlata2021), leaving only a single-peak red-skewed profile.
Narrow-band (NB) surveys have discovered a substantial sample of LAE at
![]() $z = 5.7$
and
$z = 5.7$
and
![]() $z = 6.6$
(see Hu et al. Reference Hu2010; Matthee et al. Reference Matthee2015; Santos, Sobral, & Matthee Reference Santos, Sobral and Matthee2016; Bagley et al. Reference Bagley2017; Konno et al. Reference Konno2018; Taylor et al. Reference Taylor, Barger, Cowie, Hu and Songaila2020; Taylor et al. Reference Taylor, Cowie, Barger, Hu and Songaila2021), and several LAE have also been detected at
$z = 6.6$
(see Hu et al. Reference Hu2010; Matthee et al. Reference Matthee2015; Santos, Sobral, & Matthee Reference Santos, Sobral and Matthee2016; Bagley et al. Reference Bagley2017; Konno et al. Reference Konno2018; Taylor et al. Reference Taylor, Barger, Cowie, Hu and Songaila2020; Taylor et al. Reference Taylor, Cowie, Barger, Hu and Songaila2021), and several LAE have also been detected at
![]() $z = 6.9$
(Hu et al. Reference Hu2017) and
$z = 6.9$
(Hu et al. Reference Hu2017) and
![]() $z = 7.3$
(Konno et al. Reference Konno2014). Recent data from the James Webb Space Telescope (JWST) has also contributed to the unprecedented characterisation of LAEs throughout the EoR (Tang et al. Reference Tang2023; Jung et al. Reference Jung2024; Witten et al. Reference Witten2024). The advent of giant imagers, such as Subaru/ Hyper Suprime-Cam (HSC; Miyazaki et al. Reference Miyazaki2018), has allowed detections of several rare ultra-luminous LAEs (ULLAEs) with
$z = 7.3$
(Konno et al. Reference Konno2014). Recent data from the James Webb Space Telescope (JWST) has also contributed to the unprecedented characterisation of LAEs throughout the EoR (Tang et al. Reference Tang2023; Jung et al. Reference Jung2024; Witten et al. Reference Witten2024). The advent of giant imagers, such as Subaru/ Hyper Suprime-Cam (HSC; Miyazaki et al. Reference Miyazaki2018), has allowed detections of several rare ultra-luminous LAEs (ULLAEs) with
![]() $\mathrm{log}( L_{\mathrm{Ly}\alpha} \, [\mathrm{erg} \, \mathrm{s}^{-1}]) \gt 43.5 $
(see, Songaila et al. Reference Songaila, Barger, Cowie, Hu and Taylor2022), including the detections of extremely rare double-peaked LAEs with a blue-wing (see Hu et al. Reference Hu2016; Songaila et al. Reference Songaila2018; Meyer et al. Reference Meyer, Laporte, Ellis, Verhamme and Garel2021).
$\mathrm{log}( L_{\mathrm{Ly}\alpha} \, [\mathrm{erg} \, \mathrm{s}^{-1}]) \gt 43.5 $
(see, Songaila et al. Reference Songaila, Barger, Cowie, Hu and Taylor2022), including the detections of extremely rare double-peaked LAEs with a blue-wing (see Hu et al. Reference Hu2016; Songaila et al. Reference Songaila2018; Meyer et al. Reference Meyer, Laporte, Ellis, Verhamme and Garel2021).
The Multi Unit Spectroscopic Explorer (see, Bacon et al. Reference Bacon, McLean, Ramsay and Takami2010) on the Very Large Telescope (VLT) has been instrumental in identifying faint LAEs during the EoR (up to
![]() $z \sim 6.6$
) by providing deep, high-resolution spectral data across a wide field of view, without any redshift restrictions of NB imaging (see, Hashimoto et al. Reference Hashimoto2017; Urrutia et al. Reference Urrutia2019; Kerutt et al. Reference Kerutt2022; Bacon et al. Reference Bacon2023).
$z \sim 6.6$
) by providing deep, high-resolution spectral data across a wide field of view, without any redshift restrictions of NB imaging (see, Hashimoto et al. Reference Hashimoto2017; Urrutia et al. Reference Urrutia2019; Kerutt et al. Reference Kerutt2022; Bacon et al. Reference Bacon2023).
Reionisation is known to be an inhomogeneous process (Pentericci et al. Reference Pentericci2014; Becker et al. Reference Becker2015; Bosman et al. Reference Bosman2022), indicating that galaxies in denser regions are likely to create the first ’ionised bubbles’ in the Universe (Mason et al. Reference Mason2018; Endsley et al. Reference Endsley2021a; Jung et al. Reference Jung2022b; Endsley & Stark Reference Endsley and Stark2022; Whitler et al. Reference Whitler2024), which then preferentially emit Ly
![]() $\alpha$
radiation once they reach a significant size. As a result, the most distant LAEs are vital for observing and mapping the reionisation process. Strong Ly
$\alpha$
radiation once they reach a significant size. As a result, the most distant LAEs are vital for observing and mapping the reionisation process. Strong Ly
![]() $\alpha$
emission at
$\alpha$
emission at
![]() $z \gtrsim 6$
often indicates the presence of large ionised bubbles in an otherwise neutral IGM, providing direct observational insights into the reionised regions of the early Universe. When Ly
$z \gtrsim 6$
often indicates the presence of large ionised bubbles in an otherwise neutral IGM, providing direct observational insights into the reionised regions of the early Universe. When Ly
![]() $\alpha$
photons are emitted from galaxies located within large ionised bubbles, they undergo cosmological redshifting far into the damping wing before encountering neutral hydrogen. As a result, they transmit more effectively through IGM (Weinberger et al. Reference Weinberger, Kulkarni, Haehnelt, Choudhury and Puchwein2018; Mason & Gronke Reference Mason and Gronke2020; Smith et al. Reference Smith2022; Qin et al. Reference Qin2022). Recent studies have found that Ly
$\alpha$
photons are emitted from galaxies located within large ionised bubbles, they undergo cosmological redshifting far into the damping wing before encountering neutral hydrogen. As a result, they transmit more effectively through IGM (Weinberger et al. Reference Weinberger, Kulkarni, Haehnelt, Choudhury and Puchwein2018; Mason & Gronke Reference Mason and Gronke2020; Smith et al. Reference Smith2022; Qin et al. Reference Qin2022). Recent studies have found that Ly
![]() $\alpha$
line width increases with luminosity and this trend becomes more prominent at
$\alpha$
line width increases with luminosity and this trend becomes more prominent at
![]() $z = 6.6$
(see, Matthee et al. Reference Matthee2017b; Songaila et al. Reference Songaila, Cowie, Barger, Hu and Taylor2024), where higher-luminosity LAEs with
$z = 6.6$
(see, Matthee et al. Reference Matthee2017b; Songaila et al. Reference Songaila, Cowie, Barger, Hu and Taylor2024), where higher-luminosity LAEs with
![]() $\mathrm{log}( L_{\mathrm{Ly}\alpha} \, [\mathrm{erg} \, \mathrm{s}^{-1}]) \gtrsim 43.25 $
show significantly broad Ly
$\mathrm{log}( L_{\mathrm{Ly}\alpha} \, [\mathrm{erg} \, \mathrm{s}^{-1}]) \gtrsim 43.25 $
show significantly broad Ly
![]() $\alpha$
lines (Songaila et al. Reference Songaila, Cowie, Barger, Hu and Taylor2024). At higher redshifts, the IGM becomes more neutral, increasing Ly
$\alpha$
lines (Songaila et al. Reference Songaila, Cowie, Barger, Hu and Taylor2024). At higher redshifts, the IGM becomes more neutral, increasing Ly
![]() $\alpha$
line scattering and hence narrowing of the lines is expected. The lack of this effect in brighter LAEs suggests that they reside in more ionised regions, shielding themselves from scattering.
$\alpha$
line scattering and hence narrowing of the lines is expected. The lack of this effect in brighter LAEs suggests that they reside in more ionised regions, shielding themselves from scattering.
One of the key components in determining the ionising photon budget is the ionising photon production efficiency (
![]() $\xi_{\mathrm{ion}}$
), which is defined as the ratio between the production rate of ionising photons over the non-ionising UV luminosity density. It has been found that as we delve deeper into the universe’s history, young galaxies seem to appear more efficient in producing ionising photons (see, Bouwens et al. Reference Bouwens2016; Endsley et al. Reference Endsley, Stark, Chevallard and Charlot2021b; Prieto-Lyon et al. Reference Prieto-Lyon2023; Simmonds et al. Reference Simmonds2023; Tang et al. Reference Tang2023). Moreover, UV-faint galaxies with Ly
$\xi_{\mathrm{ion}}$
), which is defined as the ratio between the production rate of ionising photons over the non-ionising UV luminosity density. It has been found that as we delve deeper into the universe’s history, young galaxies seem to appear more efficient in producing ionising photons (see, Bouwens et al. Reference Bouwens2016; Endsley et al. Reference Endsley, Stark, Chevallard and Charlot2021b; Prieto-Lyon et al. Reference Prieto-Lyon2023; Simmonds et al. Reference Simmonds2023; Tang et al. Reference Tang2023). Moreover, UV-faint galaxies with Ly
![]() $\alpha$
emission are found to have enhanced
$\alpha$
emission are found to have enhanced
![]() $\xi_{\mathrm{ion}}$
(Maseda et al. Reference Maseda2020; Ning et al. Reference Ning2023; Saxena et al. Reference Saxena2024; Lin et al. Reference Lin2024) at
$\xi_{\mathrm{ion}}$
(Maseda et al. Reference Maseda2020; Ning et al. Reference Ning2023; Saxena et al. Reference Saxena2024; Lin et al. Reference Lin2024) at
![]() $z \sim 6$
, making LAEs in the reionisation era the most exciting sources for studying and constraining reionisation.
$z \sim 6$
, making LAEs in the reionisation era the most exciting sources for studying and constraining reionisation.
In this paper, we present spectroscopic properties of 22 new LAEs at the end of reionisation (
![]() $z = 5.5 - 6.6$
) found in the MUSE data obtained as a part of the Middle Ages Galaxy Properties with Integral Field Spectroscopy (MAGPI) survey (Foster et al. Reference Foster2021). We restrict this current study to redshifts of
$z = 5.5 - 6.6$
) found in the MUSE data obtained as a part of the Middle Ages Galaxy Properties with Integral Field Spectroscopy (MAGPI) survey (Foster et al. Reference Foster2021). We restrict this current study to redshifts of
![]() $z \gtrsim 5.5$
, considering the global neutral hydrogen fraction approaches
$z \gtrsim 5.5$
, considering the global neutral hydrogen fraction approaches
![]() $x_{HI}\,{\sim}\,0$
at around
$x_{HI}\,{\sim}\,0$
at around
![]() $z \sim 5.5$
in ‘late’ reionisation scenarios (Kulkarni et al. Reference Kulkarni2019; Bosman et al. Reference Bosman2022). We constrain the evolution of Ly
$z \sim 5.5$
in ‘late’ reionisation scenarios (Kulkarni et al. Reference Kulkarni2019; Bosman et al. Reference Bosman2022). We constrain the evolution of Ly
![]() $\alpha$
line width as a function of Ly
$\alpha$
line width as a function of Ly
![]() $\alpha$
luminosity up to
$\alpha$
luminosity up to
![]() $z\,{\sim}\,7$
. Using spectroscopic information of these LAEs, along with the Subaru Hyper-Suprime Cam (HSC) optical photometric information, we estimate their ionising photon contribution toward the global reionisation budget. We also estimate the size of ionised bubbles around these LAEs to investigate the mechanism leading to the visibility of strong Ly
$z\,{\sim}\,7$
. Using spectroscopic information of these LAEs, along with the Subaru Hyper-Suprime Cam (HSC) optical photometric information, we estimate their ionising photon contribution toward the global reionisation budget. We also estimate the size of ionised bubbles around these LAEs to investigate the mechanism leading to the visibility of strong Ly
![]() $\alpha$
emission even beyond
$\alpha$
emission even beyond
![]() $z \gt 6$
.
$z \gt 6$
.
The layout of this paper is as follows: In Section 2, we describe the reduction and selection of MUSE data of potential LAE candidates along with the extraction of HSC photometric magnitudes. Section 3 explores the data analyses: Ly
![]() $\alpha$
line fitting and spectroscopic and photometric measurements. Section 4 presents results on the evolution of the Ly
$\alpha$
line fitting and spectroscopic and photometric measurements. Section 4 presents results on the evolution of the Ly
![]() $\alpha$
line widths and give an insight into the potential ionised bubbles surrounding these LAEs and also discusses these findings in context of previous works. The main conclusions and summary of this study are presented in Section 5. Throughout this paper, we assume a standard flat
$\alpha$
line widths and give an insight into the potential ionised bubbles surrounding these LAEs and also discusses these findings in context of previous works. The main conclusions and summary of this study are presented in Section 5. Throughout this paper, we assume a standard flat
![]() $\Lambda$
CDM cosmology with parameters
$\Lambda$
CDM cosmology with parameters
![]() $H_0$
= 70
$H_0$
= 70
![]() $\mathrm{km} \, \mathrm{s}^{-1} \mathrm{Mpc}^{-1}$
,
$\mathrm{km} \, \mathrm{s}^{-1} \mathrm{Mpc}^{-1}$
,
![]() $\Omega_{\mathrm{m}}$
=
$\Omega_{\mathrm{m}}$
=
![]() $0.3$
, and
$0.3$
, and
![]() $\Omega_{\Lambda}$
=
$\Omega_{\Lambda}$
=
![]() $0.7$
.
$0.7$
.
2. Observations and data
2.1 MUSE spectroscopic data
The MAGPI surveyFootnote a is an ongoing Large Program on the VLT/MUSE, targeting 56 fields from the Galaxy and Mass Assembly (GAMA; Driver et al. Reference Driver2011) G12, G15, and G23 fields. MAGPI also includes archival observations of legacy fields Abell 370 and Abell 2744. The survey targets a total of 60 primary galaxies with stellar masses
![]() $M_{*} \gt 7 \times10^{10}$
M
$M_{*} \gt 7 \times10^{10}$
M
![]() $_\odot$
and
$_\odot$
and
![]() $\sim$
100 satellite galaxies with
$\sim$
100 satellite galaxies with
![]() $M_{*} \gt 10^{9}$
M
$M_{*} \gt 10^{9}$
M
![]() $_\odot$
. The primary objective of MAGPI is to conduct a detailed spatially resolved spectroscopic analysis of stars and ionised gas within
$_\odot$
. The primary objective of MAGPI is to conduct a detailed spatially resolved spectroscopic analysis of stars and ionised gas within
![]() $0.25 \lt z \lt 0.35$
galaxies (see Foster et al. Reference Foster2021). Data are taken using the MUSE Wide Field Mode (
$0.25 \lt z \lt 0.35$
galaxies (see Foster et al. Reference Foster2021). Data are taken using the MUSE Wide Field Mode (
![]() $1^{\prime}\times1^{\prime}$
) with a spatial sampling rate of
$1^{\prime}\times1^{\prime}$
) with a spatial sampling rate of
![]() $0.2^{\prime\prime}$
/pixel and the median Full Width at Half Maximum (FWHM) is
$0.2^{\prime\prime}$
/pixel and the median Full Width at Half Maximum (FWHM) is
![]() $0.64^{\prime\prime}$
in g band,
$0.64^{\prime\prime}$
in g band,
![]() $0.6^{\prime\prime}$
in r band and
$0.6^{\prime\prime}$
in r band and
![]() $0.55^{\prime\prime}$
in i band. Each field is observed in six observing blocks, each comprising 2
$0.55^{\prime\prime}$
in i band. Each field is observed in six observing blocks, each comprising 2
![]() $\times$
1 320 s exposures, resulting in a total integration time of
$\times$
1 320 s exposures, resulting in a total integration time of
![]() $4.4$
h. The survey primarily employs the nominal mode, providing a wavelength coverage ranging from
$4.4$
h. The survey primarily employs the nominal mode, providing a wavelength coverage ranging from
![]() $4\,700$
to
$4\,700$
to
![]() $9\,350$
Å, with a dispersion of
$9\,350$
Å, with a dispersion of
![]() $1.25$
Å. Ground-layer adaptive optics (GLAO) is used to correct atmospheric seeing effects, resulting in a gap between
$1.25$
Å. Ground-layer adaptive optics (GLAO) is used to correct atmospheric seeing effects, resulting in a gap between
![]() $5\,805$
and
$5\,805$
and
![]() $5\,965$
Å due to the GALACSI laser notch filter. The depth of MAGPI data allows for the detection of both foreground sources within the Local Universe and distant background sources, including LAEs at
$5\,965$
Å due to the GALACSI laser notch filter. The depth of MAGPI data allows for the detection of both foreground sources within the Local Universe and distant background sources, including LAEs at
![]() $ 2.9 \lesssim z \lesssim 6.6$
.
$ 2.9 \lesssim z \lesssim 6.6$
.
The raw MUSE data cubes are reduced using Pymusepipe2
Footnote b, a Python wrapper for the ESO MUSE reduction pipeline (Weilbacher et al. Reference Weilbacher2020). This pipeline is used to perform the standard bias and overscan subtraction, flat-fielding, wavelength calibration, and telluric correction. Additional information about the data reduction process is provided in Foster et al. (Reference Foster2021) and it will be presented in a greater detail (Mendel et al. in prep.). LSDCat
Footnote c (Herenz & Wisotzki Reference Herenz and Wisotzki2017) was used for the identification of faint sources – particularly LAEs – accompanied by both automated and visual inspection. LAEs are confirmed using visual inspections of line-profiles and using MARZ
Footnote d redshifting software (Hinton et al. Reference Hinton, Davis, Lidman, Glazebrook and Lewis2016) to rule out interlopers. This search led to the detection of 380 new LAEs distributed across 35 MAGPI fields (Mukherjee et al. in preparation). Among these, we found 22 LAEs with
![]() $\mathrm{log} \,( L_{\mathrm{Ly}\alpha} \, [\mathrm{erg} \, \mathrm{s}^{-1}]) \gt 42.4 $
at
$\mathrm{log} \,( L_{\mathrm{Ly}\alpha} \, [\mathrm{erg} \, \mathrm{s}^{-1}]) \gt 42.4 $
at
![]() $5.5 \lesssim z \lesssim 6.6$
.
$5.5 \lesssim z \lesssim 6.6$
.
2.2 HSC photometry
We use optical photometric data for 17 MAGPI LAEs of our sample that are covered in the broad-band filters (g, r, i, z and y) of Subaru HSC Wide layer. HSC Strategic Program (see Aihara et al. Reference Aihara2018) is a wide-field optical imaging survey on the
![]() $8.2$
meter Subaru Telescope. The HSC-Wide layer data cover about 300
$8.2$
meter Subaru Telescope. The HSC-Wide layer data cover about 300
![]() $\mathrm{deg}^2$
in all five broad-band filters to the nominal survey exposure (10 min in g and r bands and 20 min in i, z, and y bands; see Aihara et al. Reference Aihara2019) with a median seeing
$\mathrm{deg}^2$
in all five broad-band filters to the nominal survey exposure (10 min in g and r bands and 20 min in i, z, and y bands; see Aihara et al. Reference Aihara2019) with a median seeing
![]() $0.6^{\prime\prime}$
in the i-band.
$0.6^{\prime\prime}$
in the i-band.
Using HSC command-line SQL (Structured Query Language) toolFootnote e, we retrieve the Wide layer photometric data from data-release 2 (Aihara et al. Reference Aihara2019). We extract fluxes and corresponding
![]() $1 \sigma$
flux uncertainties and limiting
$1 \sigma$
flux uncertainties and limiting
![]() $2\sigma$
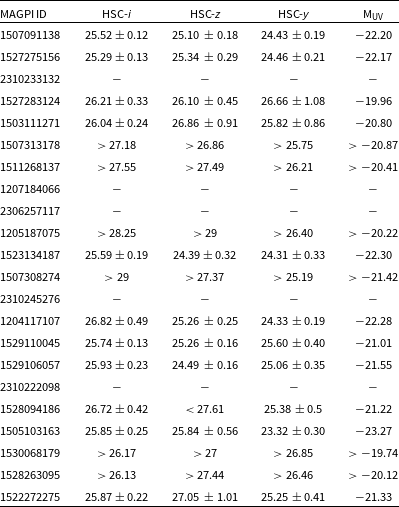
fluxes (for non-detections) using 2′′ aperture diameter. These fluxes and corresponding uncertainties for i, z, and y bands are presented in Table 1.
$2\sigma$
fluxes (for non-detections) using 2′′ aperture diameter. These fluxes and corresponding uncertainties for i, z, and y bands are presented in Table 1.
Table 1. HSC photometry of MAGPI LAEs at
![]() $z = 5.5 - 6.6$
, in order of increasing redshift. HSC-i, z and y band AB magnitudes, and
$z = 5.5 - 6.6$
, in order of increasing redshift. HSC-i, z and y band AB magnitudes, and
![]() $2\sigma$
limits (for non-detections) are presented.
$2\sigma$
limits (for non-detections) are presented.
![]() $\mathrm{M}_{\mathrm{UV}}$
is the rest-frame absolute UV magnitude estimated from the y-band magnitudes.
$\mathrm{M}_{\mathrm{UV}}$
is the rest-frame absolute UV magnitude estimated from the y-band magnitudes.
3. Data analyses
For our sample of 22 LAEs, 1D spectra are extracted using an aperture of 2′′ radius. MUSE 1D spectra reveal the detection of Ly
![]() $\alpha$
emissions where spectroscopic redshifts are determined based on the peak of the Ly
$\alpha$
emissions where spectroscopic redshifts are determined based on the peak of the Ly
![]() $\alpha$
line. No other associated emission lines are found in the MUSE data for these 22 LAEs, restricting the measurement of systemic redshift. Below we estimate UV magnitudes and discuss the procedures of analysing Ly
$\alpha$
line. No other associated emission lines are found in the MUSE data for these 22 LAEs, restricting the measurement of systemic redshift. Below we estimate UV magnitudes and discuss the procedures of analysing Ly
![]() $\alpha$
spectra to study properties of these LAEs.
$\alpha$
spectra to study properties of these LAEs.
3.1 Estimating UV magnitudes
Out of the 22 sources, 11 LAEs are detected in HSC broad-band filters. HSC does not cover GAMA23 fields and hence we do not have photometric data for four sources in this field. We also do not have photometric data for MAGPI1207184066 as it is located at the edge of the HSC field. For rest of the six sources, which are not detected in HSC, we calculate a
![]() $2\, \sigma$
limit on the magnitudes (see Table 1). As we do not have photometry beyond y band, no meaningful constraints can be obtained on the UV slope (
$2\, \sigma$
limit on the magnitudes (see Table 1). As we do not have photometry beyond y band, no meaningful constraints can be obtained on the UV slope (
![]() $\beta$
). Therefore, we assume a flat UV slope
$\beta$
). Therefore, we assume a flat UV slope
![]() $\beta = -2$
, which is the typical value that most of the high-redshift galaxies have (see, Dunlop et al. Reference Dunlop2013; Bouwens et al. Reference Bouwens2014; Matthee et al. Reference Matthee2017b). We convert the y band magnitudes to the rest-frame absolute UV magnitudes (
$\beta = -2$
, which is the typical value that most of the high-redshift galaxies have (see, Dunlop et al. Reference Dunlop2013; Bouwens et al. Reference Bouwens2014; Matthee et al. Reference Matthee2017b). We convert the y band magnitudes to the rest-frame absolute UV magnitudes (
![]() $\mathrm{M}_{\mathrm{UV}}$
) at
$\mathrm{M}_{\mathrm{UV}}$
) at
![]() $1\,500$
Å. We also note that, for
$1\,500$
Å. We also note that, for
![]() $z \gt 6$
sources, y-band magnitude is not exactly measuring the flux at
$z \gt 6$
sources, y-band magnitude is not exactly measuring the flux at
![]() $1\,500$
Å. Still, it provides a decent approximation of the UV magnitudes. The estimated UV magnitudes of our sources lie in the range
$1\,500$
Å. Still, it provides a decent approximation of the UV magnitudes. The estimated UV magnitudes of our sources lie in the range
![]() $-19.74 \lesssim \mathrm{M}_{\mathrm{UV}} \lesssim -23.27$
, which are given in Table 1.
$-19.74 \lesssim \mathrm{M}_{\mathrm{UV}} \lesssim -23.27$
, which are given in Table 1.
3.2 Line profile fitting
We use pyplatefit,Footnote f a python module (Bacon et al. Reference Bacon2023) to fit a local continuum and obtain a continuum subtracted spectrum. pyplatefit performs a continuum fit around the observed Ly
![]() $\alpha$
line in a spectral window of
$\alpha$
line in a spectral window of
![]() $\pm 50$
Å centred on the Ly
$\pm 50$
Å centred on the Ly
![]() $\alpha$
line, using a simple stellar population model (Bruzual & Charlot Reference Bruzual and Charlot2003). It then subtracts the continuum and returns a continuum-subtracted spectrum. Next we fit the continuum subtracted Ly
$\alpha$
line, using a simple stellar population model (Bruzual & Charlot Reference Bruzual and Charlot2003). It then subtracts the continuum and returns a continuum-subtracted spectrum. Next we fit the continuum subtracted Ly
![]() $\alpha$
profiles using an asymmetric Gaussian which has been found to provide an extremely good representation of the Ly
$\alpha$
profiles using an asymmetric Gaussian which has been found to provide an extremely good representation of the Ly
![]() $\alpha$
line (see Shibuya et al. Reference Shibuya2014; Herenz et al. Reference Herenz2017; Claeyssens et al. Reference Claeyssens2019; Songaila et al. Reference Songaila, Cowie, Barger, Hu and Taylor2024):
$\alpha$
line (see Shibuya et al. Reference Shibuya2014; Herenz et al. Reference Herenz2017; Claeyssens et al. Reference Claeyssens2019; Songaila et al. Reference Songaila, Cowie, Barger, Hu and Taylor2024):
where
![]() $f_{\mathrm{max}}$
is the flux normalisation (amplitude),
$f_{\mathrm{max}}$
is the flux normalisation (amplitude),
![]() $\Delta v$
is the velocity shift (in
$\Delta v$
is the velocity shift (in
![]() $\mathrm{km}\, \mathrm{s}^{-1}$
) relative to the peak velocity,
$\mathrm{km}\, \mathrm{s}^{-1}$
) relative to the peak velocity,
![]() $a_{\mathrm{asym}}$
determines the asymmetry or skewness of the line and w (in
$a_{\mathrm{asym}}$
determines the asymmetry or skewness of the line and w (in
![]() $\mathrm{km}\, \mathrm{s}^{-1}$
) controls the line width (FWHM). A positive asymmetry value suggests that the Ly
$\mathrm{km}\, \mathrm{s}^{-1}$
) controls the line width (FWHM). A positive asymmetry value suggests that the Ly
![]() $\alpha$
line has a red wing, which is usually seen in most of the single-peaked Ly
$\alpha$
line has a red wing, which is usually seen in most of the single-peaked Ly
![]() $\alpha$
lines (Kerutt et al. Reference Kerutt2022; Songaila et al. Reference Songaila, Barger, Cowie, Hu and Taylor2022). The line width can be obtained in terms of fitting parameters as follows (see also, Claeyssens et al. Reference Claeyssens2019; Songaila et al. Reference Songaila, Cowie, Barger, Hu and Taylor2024):
$\alpha$
lines (Kerutt et al. Reference Kerutt2022; Songaila et al. Reference Songaila, Barger, Cowie, Hu and Taylor2022). The line width can be obtained in terms of fitting parameters as follows (see also, Claeyssens et al. Reference Claeyssens2019; Songaila et al. Reference Songaila, Cowie, Barger, Hu and Taylor2024):
The corresponding error in the FWHM is almost fully dominated by the error in w, with only a few percent contribution from the asymmetry term. The fits on the continuum-subtracted spectra along with the values of the free parameters and corresponding
![]() $1 \sigma$
errors are shown in Appendix 1.
$1 \sigma$
errors are shown in Appendix 1.
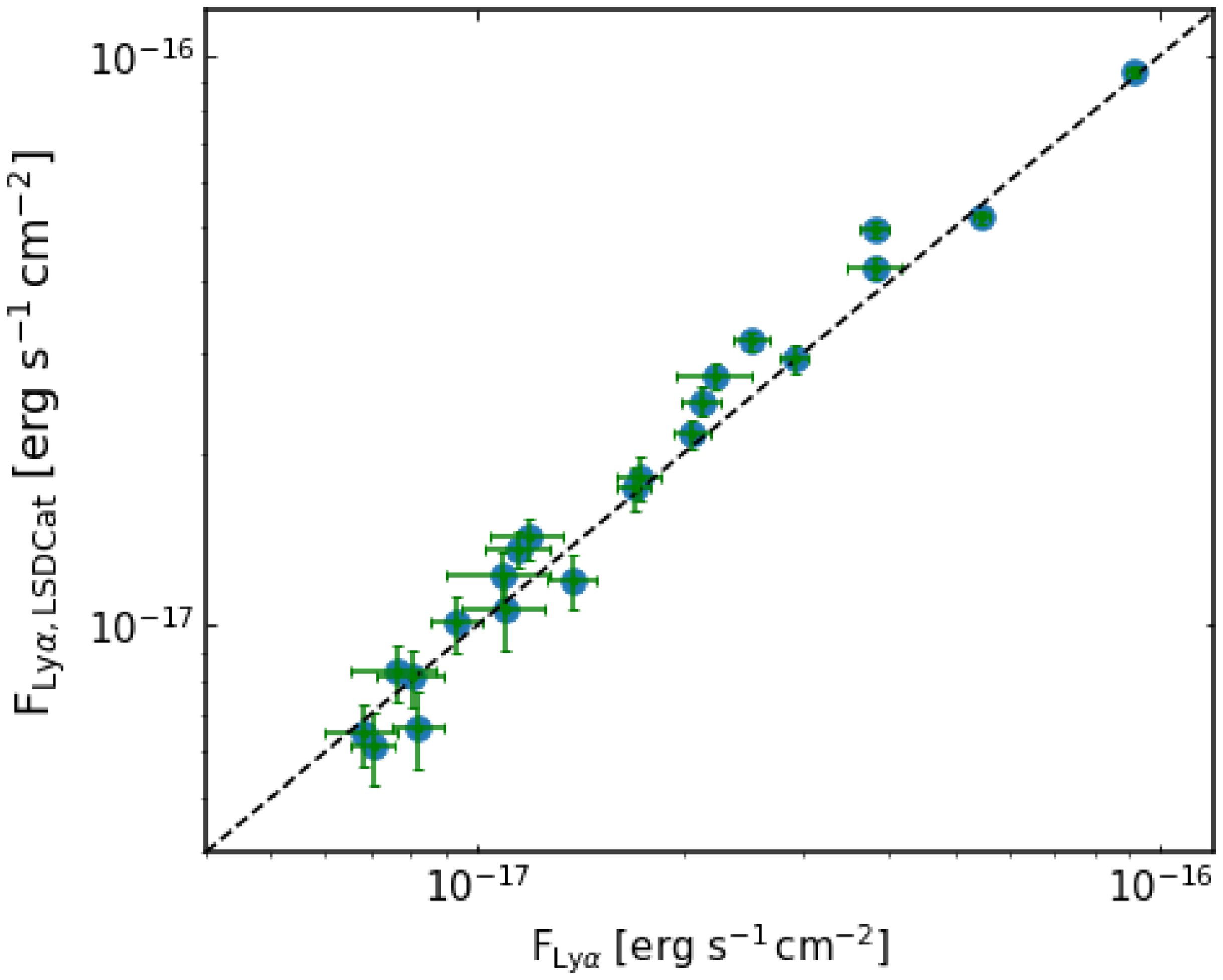
Figure 1. Ly
![]() $\alpha$
line fluxes obtained from MUSE 1D spectra (extracted using 2′′ radius aperture) are compared against LSDCat
$\alpha$
line fluxes obtained from MUSE 1D spectra (extracted using 2′′ radius aperture) are compared against LSDCat
![]() $3\, R_{\mathrm{KRON}}$
fluxes. The one-to-one relation is shown as the dashed line.
$3\, R_{\mathrm{KRON}}$
fluxes. The one-to-one relation is shown as the dashed line.
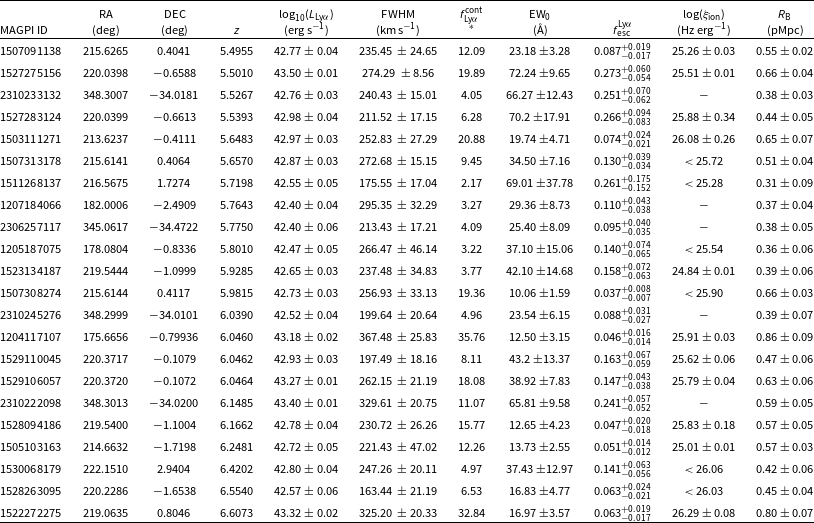
Table 2. Properties of 22 MAGPI LAEs at
![]() $5.5 \lesssim z \lesssim 6.6$
in the sample, in order of increasing redshift. Columns are as follows: MAGPI ID; RA: Right Ascension in degrees; DEC: Declination in degrees; z: Redshift based on the peak of the Ly
$5.5 \lesssim z \lesssim 6.6$
in the sample, in order of increasing redshift. Columns are as follows: MAGPI ID; RA: Right Ascension in degrees; DEC: Declination in degrees; z: Redshift based on the peak of the Ly
![]() $\alpha$
line;
$\alpha$
line;
![]() $\mathrm{log}_{10}(L_{\mathrm{Ly}\alpha})$
: observed Ly
$\mathrm{log}_{10}(L_{\mathrm{Ly}\alpha})$
: observed Ly
![]() $\alpha$
luminosity in
$\alpha$
luminosity in
![]() $\mathrm{erg}\, \mathrm{s}^{-1}$
; FWHM: Ly
$\mathrm{erg}\, \mathrm{s}^{-1}$
; FWHM: Ly
![]() $\alpha$
line width measured using asymmetric Gaussian fit;
$\alpha$
line width measured using asymmetric Gaussian fit;
![]() $f^{\mathrm{cont}}_{\mathrm{Ly}\alpha}$
*: Observed UV-continuum flux-density at the location of Ly
$f^{\mathrm{cont}}_{\mathrm{Ly}\alpha}$
*: Observed UV-continuum flux-density at the location of Ly
![]() $\alpha$
wavelength, in
$\alpha$
wavelength, in
![]() $10^{-20} \, \mathrm{erg}\, \mathrm{s}^{-1} \mathrm{cm}^{-2}$
Å–1;
$10^{-20} \, \mathrm{erg}\, \mathrm{s}^{-1} \mathrm{cm}^{-2}$
Å–1;
![]() $\mathrm{EW}_{0}$
: Spectroscopically measured Ly
$\mathrm{EW}_{0}$
: Spectroscopically measured Ly
![]() $\alpha$
rest-frame equivalent width;
$\alpha$
rest-frame equivalent width;
![]() $f^{\mathrm{Ly}\alpha}_{\mathrm{esc}}$
: Ly
$f^{\mathrm{Ly}\alpha}_{\mathrm{esc}}$
: Ly
![]() $\alpha$
escape fraction;
$\alpha$
escape fraction;
![]() $\mathrm{log}(\xi_{\mathrm{ion}})$
: Ionising photon production efficiency in
$\mathrm{log}(\xi_{\mathrm{ion}})$
: Ionising photon production efficiency in
![]() $\mathrm{Hz}\, \mathrm{erg}^{-1}$
;
$\mathrm{Hz}\, \mathrm{erg}^{-1}$
;
![]() $R_{\mathrm{B}}$
: radius of bubble ionised by LAE itself, in pMpc.
$R_{\mathrm{B}}$
: radius of bubble ionised by LAE itself, in pMpc.
3.3 Spectroscopic measurements
Using a single asymmetric Gaussian fit to the Ly
![]() $\alpha$
profile extracted using 2′′ radius aperture, as mentioned above, we measure Ly
$\alpha$
profile extracted using 2′′ radius aperture, as mentioned above, we measure Ly
![]() $\alpha$
line fluxes (
$\alpha$
line fluxes (
![]() $F_{\mathrm{Ly}\alpha}$
) for our LAEs. In Fig. 1, we compare them with the
$F_{\mathrm{Ly}\alpha}$
) for our LAEs. In Fig. 1, we compare them with the
![]() $3\, R_{\mathrm{KRON}}$
fluxes obtained using LSDCat (flux extracted using the aperture of radius
$3\, R_{\mathrm{KRON}}$
fluxes obtained using LSDCat (flux extracted using the aperture of radius
![]() $3\times R_{\mathrm{KRON}}$
that contains
$3\times R_{\mathrm{KRON}}$
that contains
![]() $ \gt 95$
% of the total line flux; (see, Graham & Driver Reference Graham and Driver2005; Herenz et al. Reference Herenz2017). The values of
$ \gt 95$
% of the total line flux; (see, Graham & Driver Reference Graham and Driver2005; Herenz et al. Reference Herenz2017). The values of
![]() $3\, R_{\mathrm{KRON}}$
radii in which fluxes were extracted are ranging from
$3\, R_{\mathrm{KRON}}$
radii in which fluxes were extracted are ranging from
![]() $1.6^{\prime\prime}$
to
$1.6^{\prime\prime}$
to
![]() $2.2^{\prime\prime}$
. Since both flux values match well, we conclude that our line flux measurements are accurate. The observed Ly
$2.2^{\prime\prime}$
. Since both flux values match well, we conclude that our line flux measurements are accurate. The observed Ly
![]() $\alpha$
luminosities (
$\alpha$
luminosities (
![]() $L_{\mathrm{Ly}\alpha}$
) are then calculated from fluxes as
$L_{\mathrm{Ly}\alpha}$
) are then calculated from fluxes as
![]() $L_{\mathrm{Ly}\alpha} = 4 \pi \, F_{\mathrm{Ly}\alpha} D^{\,2}_{\mathrm{L}} $
, where
$L_{\mathrm{Ly}\alpha} = 4 \pi \, F_{\mathrm{Ly}\alpha} D^{\,2}_{\mathrm{L}} $
, where
![]() $D_{\mathrm{L}}$
is the luminosity distance, calculated using the cosmological parameters that we assume in Section 1.
$D_{\mathrm{L}}$
is the luminosity distance, calculated using the cosmological parameters that we assume in Section 1.
We measure the Ly
![]() $\alpha$
$\alpha$
![]() $\mathrm{EW}_{0}$
to investigate the strength of the Ly
$\mathrm{EW}_{0}$
to investigate the strength of the Ly
![]() $\alpha$
line. In order to do that, we need measurements of UV continuum flux density at the Ly
$\alpha$
line. In order to do that, we need measurements of UV continuum flux density at the Ly
![]() $\alpha$
wavelength. However, due to lack of UV-slope measurement (see Section 3.1), it is not possible to determine continuum flux density from the photometric data. Further, Hashimoto et al. (Reference Hashimoto2017) caution that fixing the value of UV-slope
$\alpha$
wavelength. However, due to lack of UV-slope measurement (see Section 3.1), it is not possible to determine continuum flux density from the photometric data. Further, Hashimoto et al. (Reference Hashimoto2017) caution that fixing the value of UV-slope
![]() $\beta$
at high-redshift can lead to an underestimation of
$\beta$
at high-redshift can lead to an underestimation of
![]() $\mathrm{EW}_{0}$
due to the redshift evolution of
$\mathrm{EW}_{0}$
due to the redshift evolution of
![]() $\beta$
. Therefore, we obtain the observed median UV-continuum flux density (
$\beta$
. Therefore, we obtain the observed median UV-continuum flux density (
![]() $f^{\mathrm{cont}}_{\mathrm{Ly}\alpha}$
) from the continuum fit performed using pyplatefit (see Section 3.2). We then divide the total Ly
$f^{\mathrm{cont}}_{\mathrm{Ly}\alpha}$
) from the continuum fit performed using pyplatefit (see Section 3.2). We then divide the total Ly
![]() $\alpha$
line flux (
$\alpha$
line flux (
![]() $ \mathrm{F}_{\mathrm{Ly}\alpha} $
) by
$ \mathrm{F}_{\mathrm{Ly}\alpha} $
) by
![]() $f^{\mathrm{cont}}_{\mathrm{Ly}\alpha}$
to determine observed Ly
$f^{\mathrm{cont}}_{\mathrm{Ly}\alpha}$
to determine observed Ly
![]() $\alpha$
equivalent width (EW). The rest-frame equivalent width is then given as
$\alpha$
equivalent width (EW). The rest-frame equivalent width is then given as
![]() $\mathrm{EW}_{0} = \mathrm{EW} / (1 + z)$
. We note that for some LAEs, the continuum in the MUSE data is too faint, and thus we can only derive lower limits for
$\mathrm{EW}_{0} = \mathrm{EW} / (1 + z)$
. We note that for some LAEs, the continuum in the MUSE data is too faint, and thus we can only derive lower limits for
![]() $\mathrm{EW}_{0}$
for them. As H
$\mathrm{EW}_{0}$
for them. As H
![]() $\alpha$
emission is not covered within the MUSE spectral range, Ly
$\alpha$
emission is not covered within the MUSE spectral range, Ly
![]() $\alpha$
escape fraction cannot be directly measured. A strong correlation between
$\alpha$
escape fraction cannot be directly measured. A strong correlation between
![]() $f^{\mathrm{Ly}\alpha}_{\mathrm{esc}}$
and
$f^{\mathrm{Ly}\alpha}_{\mathrm{esc}}$
and
![]() $\mathrm{EW}_{0}$
has been found in both low- and high-redshift LAEs (see, Matthee et al. Reference Matthee2017b; Yang et al. Reference Yang2017; Sobral & Matthee Reference Sobral and Matthee2019; Begley et al. Reference Begley2024). In Begley et al. (Reference Begley2024), a sample of 152 star-forming galaxies with
$\mathrm{EW}_{0}$
has been found in both low- and high-redshift LAEs (see, Matthee et al. Reference Matthee2017b; Yang et al. Reference Yang2017; Sobral & Matthee Reference Sobral and Matthee2019; Begley et al. Reference Begley2024). In Begley et al. (Reference Begley2024), a sample of 152 star-forming galaxies with
![]() $z \sim 4 - 5$
is used to obtain a linear dependence between
$z \sim 4 - 5$
is used to obtain a linear dependence between
![]() $f^{\mathrm{Ly}\alpha}_{\mathrm{esc}}$
and
$f^{\mathrm{Ly}\alpha}_{\mathrm{esc}}$
and
![]() $\mathrm{EW}_{0}$
. We estimate
$\mathrm{EW}_{0}$
. We estimate
![]() $f^{\mathrm{Ly}\alpha}_{\mathrm{esc}}$
using this best-fit relation. We tabulate the spectroscopic properties of these LAEs in Table 2.
$f^{\mathrm{Ly}\alpha}_{\mathrm{esc}}$
using this best-fit relation. We tabulate the spectroscopic properties of these LAEs in Table 2.
Begley et al. (Reference Begley2024) discuss that their
![]() $f^{\mathrm{Ly}\alpha}_{\mathrm{esc}}$
-
$f^{\mathrm{Ly}\alpha}_{\mathrm{esc}}$
-
![]() $\mathrm{EW}_{0}$
relation agrees well with the relation derived for low-redshift LAEs (Sobral & Matthee Reference Sobral and Matthee2019). The observed scatter in this relation are found to be well-consistent with that observed in both low and high-z LAE samples (see, Pucha et al. Reference Pucha2022; Roy et al. Reference Roy2023). A similar positive correlation has also been observed in LAEs in the reionisation era (Saxena et al. Reference Saxena2024; Tang et al. Reference Tang2024b). However, the slope, normalisation, and scatter of the observed
$\mathrm{EW}_{0}$
relation agrees well with the relation derived for low-redshift LAEs (Sobral & Matthee Reference Sobral and Matthee2019). The observed scatter in this relation are found to be well-consistent with that observed in both low and high-z LAE samples (see, Pucha et al. Reference Pucha2022; Roy et al. Reference Roy2023). A similar positive correlation has also been observed in LAEs in the reionisation era (Saxena et al. Reference Saxena2024; Tang et al. Reference Tang2024b). However, the slope, normalisation, and scatter of the observed
![]() $f^{\mathrm{Ly}\alpha}_{\mathrm{esc}}$
-
$f^{\mathrm{Ly}\alpha}_{\mathrm{esc}}$
-
![]() $\mathrm{EW}_{0}$
relationship are likely influenced by dust attenuation, differential dust geometry and
$\mathrm{EW}_{0}$
relationship are likely influenced by dust attenuation, differential dust geometry and
![]() $\xi_{\mathrm{ion}}$
(Matthee et al. Reference Matthee2017a; Harikane et al. Reference Harikane2018; Shivaei et al. Reference Shivaei2018; Sobral & Matthee Reference Sobral and Matthee2019). Additionally, for a given
$\xi_{\mathrm{ion}}$
(Matthee et al. Reference Matthee2017a; Harikane et al. Reference Harikane2018; Shivaei et al. Reference Shivaei2018; Sobral & Matthee Reference Sobral and Matthee2019). Additionally, for a given
![]() $\mathrm{EW}_{0}$
value, intrinsic scatter in
$\mathrm{EW}_{0}$
value, intrinsic scatter in
![]() $f^{\mathrm{Ly}\alpha}_{\mathrm{esc}}$
is expected due to variations in stellar populations and dust/gas properties (Begley et al. Reference Begley2024). We conclude that, despite the complexity of factors,
$f^{\mathrm{Ly}\alpha}_{\mathrm{esc}}$
is expected due to variations in stellar populations and dust/gas properties (Begley et al. Reference Begley2024). We conclude that, despite the complexity of factors,
![]() $f^{\mathrm{Ly}\alpha}_{\mathrm{esc}}$
can be predicted within
$f^{\mathrm{Ly}\alpha}_{\mathrm{esc}}$
can be predicted within
![]() $\sim$
0.5 dex of actual values from the
$\sim$
0.5 dex of actual values from the
![]() $f^{\mathrm{Ly}\alpha}_{\mathrm{esc}}$
-
$f^{\mathrm{Ly}\alpha}_{\mathrm{esc}}$
-
![]() $\mathrm{EW}_{0}$
relation of Begley et al. (Reference Begley2024) using only the equivalent width information.
$\mathrm{EW}_{0}$
relation of Begley et al. (Reference Begley2024) using only the equivalent width information.
4. Results and discussions
We present photometric and spectroscopic properties (see Tables 1 and 2, respectively) of 22 LAEs at
![]() $5.5 \lesssim z \lesssim 6.6$
. These sources have Ly
$5.5 \lesssim z \lesssim 6.6$
. These sources have Ly
![]() $\alpha$
luminosities
$\alpha$
luminosities
![]() $\mathrm{log} (L_{\mathrm{Ly}\alpha} \, [\mathrm{erg} \, \mathrm{s}^{-1}]) = 42.4 - 43.5 $
and Ly
$\mathrm{log} (L_{\mathrm{Ly}\alpha} \, [\mathrm{erg} \, \mathrm{s}^{-1}]) = 42.4 - 43.5 $
and Ly
![]() $\alpha$
rest-frame equivalent widths
$\alpha$
rest-frame equivalent widths
![]() $\mathrm{EW}_{0} \simeq 10-72$
Å. In the following subsections, we explore the relation between the Ly
$\mathrm{EW}_{0} \simeq 10-72$
Å. In the following subsections, we explore the relation between the Ly
![]() $\alpha$
line width and Ly
$\alpha$
line width and Ly
![]() $\alpha$
luminosity and investigate this relation in the context of the size of the ionised bubbles created by each LAE at the end of the reionisation era.
$\alpha$
luminosity and investigate this relation in the context of the size of the ionised bubbles created by each LAE at the end of the reionisation era.
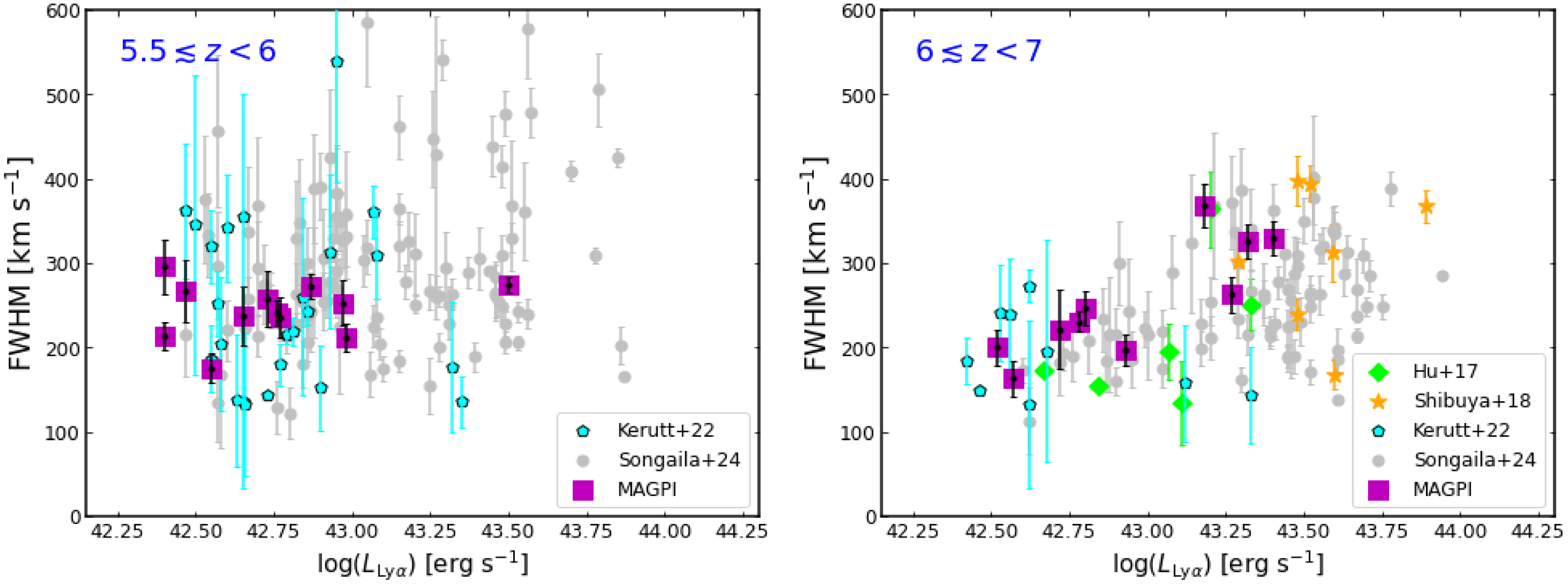
Figure 2. Evolution of Ly
![]() $\alpha$
line width is shown as function of Ly
$\alpha$
line width is shown as function of Ly
![]() $\alpha$
luminosity at
$\alpha$
luminosity at
![]() $5.5 \lesssim z \lt 6$
(left panel) and at
$5.5 \lesssim z \lt 6$
(left panel) and at
![]() $6 \lesssim z \lesssim 7$
(right panel). MAGPI LAEs (this work) are shown as purple squares. We also include data from MUSE DEEP and MUSE WIDE surveys (blue pentagons; Kerutt et al. Reference Kerutt2022), (grey circles; Songaila et al. Reference Songaila, Cowie, Barger, Hu and Taylor2024), LAGER survey (green diamonds; Hu et al. Reference Hu2017) and (orange stars; Shibuya et al. Reference Shibuya2018).
$6 \lesssim z \lesssim 7$
(right panel). MAGPI LAEs (this work) are shown as purple squares. We also include data from MUSE DEEP and MUSE WIDE surveys (blue pentagons; Kerutt et al. Reference Kerutt2022), (grey circles; Songaila et al. Reference Songaila, Cowie, Barger, Hu and Taylor2024), LAGER survey (green diamonds; Hu et al. Reference Hu2017) and (orange stars; Shibuya et al. Reference Shibuya2018).
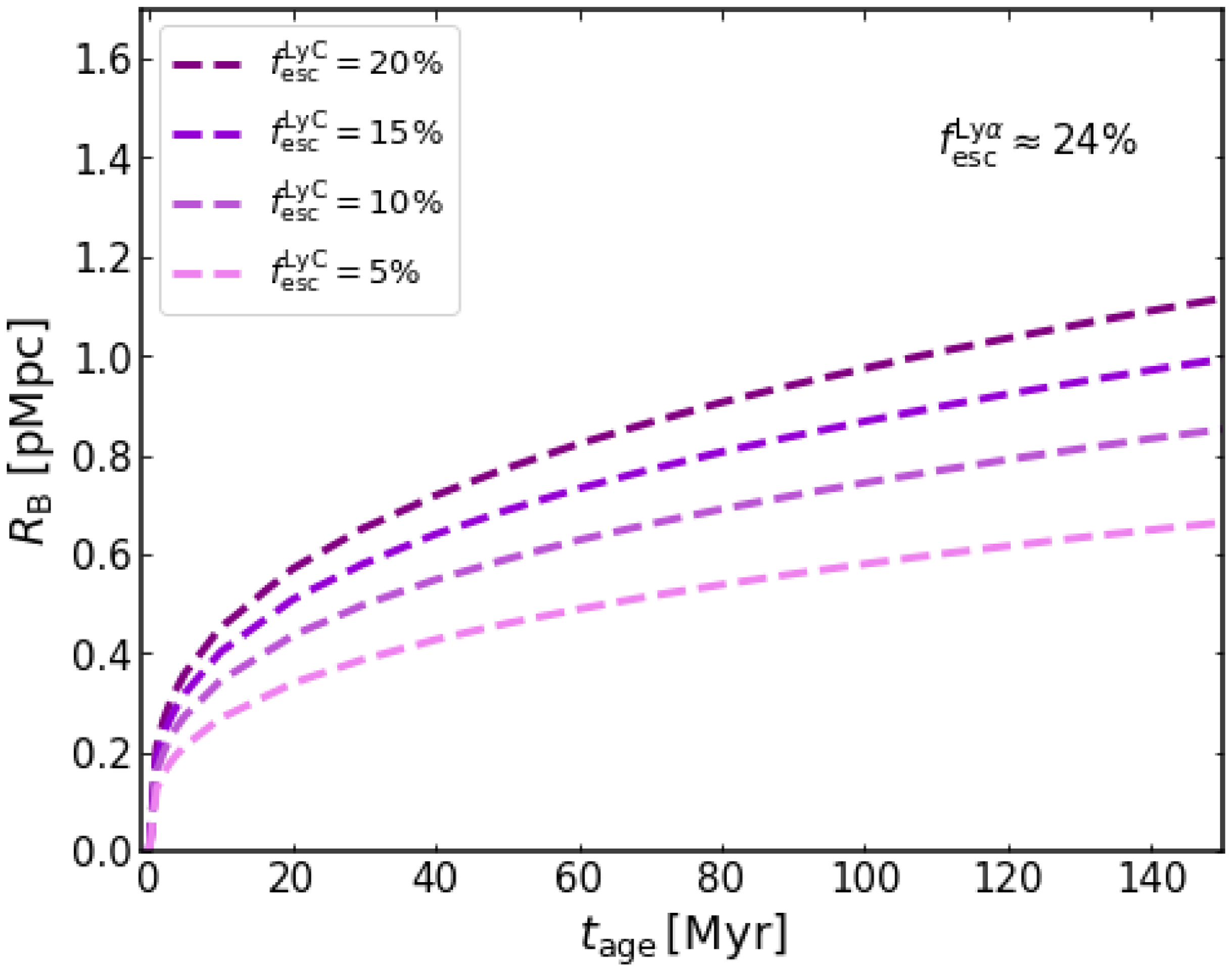
Figure 3. Radius of spherical bubble ionised by MAGPI2310222098 as a function of the age parameter (
![]() $t_{\mathrm{age}}$
), for different values of the LyC escape fraction (
$t_{\mathrm{age}}$
), for different values of the LyC escape fraction (
![]() $f^{\mathrm{LyC}}_{\mathrm{esc}} = 5$
%, 10%, 15% and 20%). Here we assume a fixed Ly
$f^{\mathrm{LyC}}_{\mathrm{esc}} = 5$
%, 10%, 15% and 20%). Here we assume a fixed Ly
![]() $\alpha$
escape fraction
$\alpha$
escape fraction
![]() $f^{\mathrm{Ly}\alpha}_{\mathrm{esc}} = 24$
%, as estimated (see Table 2).
$f^{\mathrm{Ly}\alpha}_{\mathrm{esc}} = 24$
%, as estimated (see Table 2).
4.1 Evolution of the Ly
 $\alpha$
line width
$\alpha$
line width
We fit the Ly
![]() $\alpha$
lines with an asymmetric/skewed Gaussian. This provides excellent representation of all the Ly
$\alpha$
lines with an asymmetric/skewed Gaussian. This provides excellent representation of all the Ly
![]() $\alpha$
profiles. All of the asymmetry parameters are positive, corresponding to red-skewed profiles. The asymmetry of all the lines also confirm that these are Ly
$\alpha$
profiles. All of the asymmetry parameters are positive, corresponding to red-skewed profiles. The asymmetry of all the lines also confirm that these are Ly
![]() $\alpha$
emission from star-forming galaxies rather than other emission lines from low-redshift interlopers. In Fig. 2, we present the evolution of Ly
$\alpha$
emission from star-forming galaxies rather than other emission lines from low-redshift interlopers. In Fig. 2, we present the evolution of Ly
![]() $\alpha$
line widths with Ly
$\alpha$
line widths with Ly
![]() $\alpha$
luminosities across two redshifts ranges. For MAGPI LAEs, we find that at
$\alpha$
luminosities across two redshifts ranges. For MAGPI LAEs, we find that at
![]() $z \lt 6$
(see Fig. 3, left panel), FWHM distribution is almost uniform, with no significant evolution with increasing luminosities. In contrast,
$z \lt 6$
(see Fig. 3, left panel), FWHM distribution is almost uniform, with no significant evolution with increasing luminosities. In contrast,
![]() $z \gt 6$
LAEs show a strong evolution of increasing line width with increasing luminosities (see Fig. 2, right panel). For comparison, we also include data from MUSE DEEP and MUSE WIDE surveys (Kerutt et al. Reference Kerutt2022), bright LAEs from Shibuya et al. (Reference Shibuya2018),
$z \gt 6$
LAEs show a strong evolution of increasing line width with increasing luminosities (see Fig. 2, right panel). For comparison, we also include data from MUSE DEEP and MUSE WIDE surveys (Kerutt et al. Reference Kerutt2022), bright LAEs from Shibuya et al. (Reference Shibuya2018),
![]() $z \sim 6.9 $
LAEs from LAGER survey (Hu et al. Reference Hu2017) and recent large sample of LAEs from Songaila et al. (Reference Songaila, Cowie, Barger, Hu and Taylor2024), which allows a better understanding of the evolution of line widths across a wide redshift range (
$z \sim 6.9 $
LAEs from LAGER survey (Hu et al. Reference Hu2017) and recent large sample of LAEs from Songaila et al. (Reference Songaila, Cowie, Barger, Hu and Taylor2024), which allows a better understanding of the evolution of line widths across a wide redshift range (
![]() $5.5 \lesssim z \lesssim 7$
) at the edge of reionisation. We note large uncertainties in luminosities and FWHMs in the data of Kerutt et al. (Reference Kerutt2022). Apart from that, we find our result is well-consistent with the others. We note that, at
$5.5 \lesssim z \lesssim 7$
) at the edge of reionisation. We note large uncertainties in luminosities and FWHMs in the data of Kerutt et al. (Reference Kerutt2022). Apart from that, we find our result is well-consistent with the others. We note that, at
![]() $z \gt 6$
, line widths of MAGPI LAEs are narrower (FWHM
$z \gt 6$
, line widths of MAGPI LAEs are narrower (FWHM
![]() $\lesssim 250 \, \mathrm{km}\, \mathrm{s}^{-1}$
) at luminosities
$\lesssim 250 \, \mathrm{km}\, \mathrm{s}^{-1}$
) at luminosities
![]() $\mathrm{log}(L_{\mathrm{Ly}\alpha}\, [\mathrm{erg}\, \mathrm{s}^{-1}]) \lt 43 $
, as compared to LAEs at
$\mathrm{log}(L_{\mathrm{Ly}\alpha}\, [\mathrm{erg}\, \mathrm{s}^{-1}]) \lt 43 $
, as compared to LAEs at
![]() $\mathrm{log}(L_{\mathrm{Ly}\alpha}\, [\mathrm{erg}\, \mathrm{s}^{-1}]) \gt 43 $
, where we find broader line widths (i.e. FWHM
$\mathrm{log}(L_{\mathrm{Ly}\alpha}\, [\mathrm{erg}\, \mathrm{s}^{-1}]) \gt 43 $
, where we find broader line widths (i.e. FWHM
![]() $ \gt 260 \, \mathrm{km}\, \mathrm{s}^{-1}$
). The visibility of Ly
$ \gt 260 \, \mathrm{km}\, \mathrm{s}^{-1}$
). The visibility of Ly
![]() $\alpha$
emission from high-redshift star-forming galaxies is primarily determined by the star formation rate and ionising photon budget, which influence the size of ionised bubbles around them that allow Ly
$\alpha$
emission from high-redshift star-forming galaxies is primarily determined by the star formation rate and ionising photon budget, which influence the size of ionised bubbles around them that allow Ly
![]() $\alpha$
photons to travel unattenuated along the line of sight (Malhotra & Rhoads Reference Malhotra and Rhoads2006). Despite the fact that increasingly neutral IGM potentially scatters most of the Ly
$\alpha$
photons to travel unattenuated along the line of sight (Malhotra & Rhoads Reference Malhotra and Rhoads2006). Despite the fact that increasingly neutral IGM potentially scatters most of the Ly
![]() $\alpha$
photons and make the line narrower, the broadening of the line at
$\alpha$
photons and make the line narrower, the broadening of the line at
![]() $z \gt 6$
suggests that the high-luminosity LAEs may preferentially lie in more highly ionised regions than the lower luminosity LAEs (Matthee et al. Reference Matthee2017b; Songaila et al. Reference Songaila, Cowie, Barger, Hu and Taylor2024), protecting themselves from the scattering effects of the IGM. In the next section, we discuss how LAEs themselves can produce ionised bubbles around them.
$z \gt 6$
suggests that the high-luminosity LAEs may preferentially lie in more highly ionised regions than the lower luminosity LAEs (Matthee et al. Reference Matthee2017b; Songaila et al. Reference Songaila, Cowie, Barger, Hu and Taylor2024), protecting themselves from the scattering effects of the IGM. In the next section, we discuss how LAEs themselves can produce ionised bubbles around them.
4.2 Ionising photon escape and size of ionised region
The absorption of ionising photons by the interstellar medium within galaxies leads to Ly
![]() $\alpha$
emissions through recombination processes, while photons that escape contribute to cosmic reionisation. The size of the ionised region (H ii bubble) around an ionising source can be estimated by solving the evolution equation of the ionising front (e.g. Cen & Haiman Reference Cen and Haiman2000; Yajima, Sugimura, & Hasegawa Reference Yajima, Sugimura and Hasegawa2018):
$\alpha$
emissions through recombination processes, while photons that escape contribute to cosmic reionisation. The size of the ionised region (H ii bubble) around an ionising source can be estimated by solving the evolution equation of the ionising front (e.g. Cen & Haiman Reference Cen and Haiman2000; Yajima, Sugimura, & Hasegawa Reference Yajima, Sugimura and Hasegawa2018):
where
![]() $R_{\mathrm{B}}$
is the proper physical radius of ionised bubble in physical Mpc (pMpc), H (z) is the Hubble parameter,
$R_{\mathrm{B}}$
is the proper physical radius of ionised bubble in physical Mpc (pMpc), H (z) is the Hubble parameter,
![]() $Q_{\mathrm{ion}}$
is the intrinsic production rate of ionising photons (in
$Q_{\mathrm{ion}}$
is the intrinsic production rate of ionising photons (in
![]() $\mathrm{s}^{-1}$
),
$\mathrm{s}^{-1}$
),
![]() $C_{\mathrm{HII}}$
is the clumping factor of ionised hydrogen and
$C_{\mathrm{HII}}$
is the clumping factor of ionised hydrogen and
![]() $\alpha_{\mathrm{rec}}$
is the temperature-dependent total recombination rate coefficient under Case B approximation (T =
$\alpha_{\mathrm{rec}}$
is the temperature-dependent total recombination rate coefficient under Case B approximation (T =
![]() $10^{4}$
K,
$10^{4}$
K,
![]() $n_{e} = 350\,\mathrm{cm}^{-3}$
). The mean hydrogen density of the IGM (
$n_{e} = 350\,\mathrm{cm}^{-3}$
). The mean hydrogen density of the IGM (
![]() $n_{\mathrm{H}}$
) scales with redshift as follows:
$n_{\mathrm{H}}$
) scales with redshift as follows:
![]() $n_{\mathrm{H}} \approx 8.5 \times 10^{-5} \, \left(\frac{1 + z}{8}\right)^{3} \, \mathrm{cm}^{-3}$
(see, Mason & Gronke Reference Mason and Gronke2020; Meyer et al. Reference Meyer, Laporte, Ellis, Verhamme and Garel2021).
$n_{\mathrm{H}} \approx 8.5 \times 10^{-5} \, \left(\frac{1 + z}{8}\right)^{3} \, \mathrm{cm}^{-3}$
(see, Mason & Gronke Reference Mason and Gronke2020; Meyer et al. Reference Meyer, Laporte, Ellis, Verhamme and Garel2021).
We can define ionising photon production rate (
![]() $Q_{\mathrm{ion}}$
) in terms of direct Ly
$Q_{\mathrm{ion}}$
) in terms of direct Ly
![]() $\alpha$
observables (see, Matthee et al. Reference Matthee2017b; Yajima et al. Reference Yajima, Sugimura and Hasegawa2018; Sobral & Matthee Reference Sobral and Matthee2019; Matthee et al. Reference Matthee2022):
$\alpha$
observables (see, Matthee et al. Reference Matthee2017b; Yajima et al. Reference Yajima, Sugimura and Hasegawa2018; Sobral & Matthee Reference Sobral and Matthee2019; Matthee et al. Reference Matthee2022):
where
![]() $c_{\mathrm{H}\alpha} = 1.36 \times 10^{-12} $
erg (under case B recombination; Kennicutt Reference Kennicutt1998; Schaerer Reference Schaerer2003). Here, we assume negligible nebular attenuation (Naidu et al. Reference Naidu2022). A detailed discussion on the role of dust in the context of Ly
$c_{\mathrm{H}\alpha} = 1.36 \times 10^{-12} $
erg (under case B recombination; Kennicutt Reference Kennicutt1998; Schaerer Reference Schaerer2003). Here, we assume negligible nebular attenuation (Naidu et al. Reference Naidu2022). A detailed discussion on the role of dust in the context of Ly
![]() $\alpha$
and LyC escape can be found in Kakiichi & Gronke (Reference Kakiichi and Gronke2021). In Section 3.3, we estimated Ly
$\alpha$
and LyC escape can be found in Kakiichi & Gronke (Reference Kakiichi and Gronke2021). In Section 3.3, we estimated Ly
![]() $\alpha$
escape fractions (within
$\alpha$
escape fractions (within
![]() $\simeq 0.5$
dex) using its linear dependence on
$\simeq 0.5$
dex) using its linear dependence on
![]() $\mathrm{EW}_0$
. However, this relation can be influenced by dust attenuation and
$\mathrm{EW}_0$
. However, this relation can be influenced by dust attenuation and
![]() $\xi_{\mathrm{ion}}$
, as discussed in Section 3.3. A prominent degeneracy between dust extinction and
$\xi_{\mathrm{ion}}$
, as discussed in Section 3.3. A prominent degeneracy between dust extinction and
![]() $\xi_{\mathrm{ion}}$
has been observed in Sobral & Matthee (Reference Sobral and Matthee2019), where higher dust extinction allows for a lower
$\xi_{\mathrm{ion}}$
has been observed in Sobral & Matthee (Reference Sobral and Matthee2019), where higher dust extinction allows for a lower
![]() $\xi_{\mathrm{ion}}$
and vice versa. Current data restrict us from accurately estimating both
$\xi_{\mathrm{ion}}$
and vice versa. Current data restrict us from accurately estimating both
![]() $f^{\mathrm{Ly}\alpha}_{\mathrm{esc}}$
and
$f^{\mathrm{Ly}\alpha}_{\mathrm{esc}}$
and
![]() $\xi_{\mathrm{ion}}$
as it requires dust-corrected H
$\xi_{\mathrm{ion}}$
as it requires dust-corrected H
![]() $\alpha$
luminosity. Direct observations of Balmer decrements and high-excitation UV lines are necessary to further validate and confirm our results.
$\alpha$
luminosity. Direct observations of Balmer decrements and high-excitation UV lines are necessary to further validate and confirm our results.
A correlation between Ly
![]() $\alpha$
and LyC escape fractions has been investigated in several observational studies and hydrodynamical simulations (Verhamme et al. Reference Verhamme2017; Chisholm et al. Reference Chisholm2018; Flury et al. Reference Flury2022; Maji et al. Reference Maji2022). Begley et al. (Reference Begley2024) find a linear dependence between
$\alpha$
and LyC escape fractions has been investigated in several observational studies and hydrodynamical simulations (Verhamme et al. Reference Verhamme2017; Chisholm et al. Reference Chisholm2018; Flury et al. Reference Flury2022; Maji et al. Reference Maji2022). Begley et al. (Reference Begley2024) find a linear dependence between
![]() $f^{\mathrm{LyC}}_{\mathrm{esc}}$
and
$f^{\mathrm{LyC}}_{\mathrm{esc}}$
and
![]() $f^{\mathrm{Ly}\alpha}_{\mathrm{esc}}$
. Using this relation, we estimate that our sources have
$f^{\mathrm{Ly}\alpha}_{\mathrm{esc}}$
. Using this relation, we estimate that our sources have
![]() $f^{\mathrm{LyC}}_{\mathrm{esc}} = 0.5 - 4$
%. Hydrodynamical and radiative transfer simulations are used to calibrate the same relation (Maji et al. Reference Maji2022), using which we get
$f^{\mathrm{LyC}}_{\mathrm{esc}} = 0.5 - 4$
%. Hydrodynamical and radiative transfer simulations are used to calibrate the same relation (Maji et al. Reference Maji2022), using which we get
![]() $f^{\mathrm{LyC}}_{\mathrm{esc}} \lt 3$
% for our sources. However, this correlation between Ly
$f^{\mathrm{LyC}}_{\mathrm{esc}} \lt 3$
% for our sources. However, this correlation between Ly
![]() $\alpha$
and LyC escape does not seem to work well for LyC leakers at higher redshifts (see, Kerutt et al. Reference Kerutt2024). Kinematics and ISM properties of high-redshift leakers are more complex (Guaita et al. Reference Guaita2015) as compared to low-redshift leakers. A spatial offset between Ly
$\alpha$
and LyC escape does not seem to work well for LyC leakers at higher redshifts (see, Kerutt et al. Reference Kerutt2024). Kinematics and ISM properties of high-redshift leakers are more complex (Guaita et al. Reference Guaita2015) as compared to low-redshift leakers. A spatial offset between Ly
![]() $\alpha$
and LyC emission has been observed in high-redshift leakers (Kerutt et al. Reference Kerutt2024; Gupta et al. 2024), which indicates that the two are escaping from different locations in the galaxy. For instance, high-redshift leakers prefer asymmetric escape (indicating scattering or expanding gas) rather than through optically thin ionised channel, which seems to be the case for low-redshift leakers (Kerutt et al. Reference Kerutt2024).
$\alpha$
and LyC emission has been observed in high-redshift leakers (Kerutt et al. Reference Kerutt2024; Gupta et al. 2024), which indicates that the two are escaping from different locations in the galaxy. For instance, high-redshift leakers prefer asymmetric escape (indicating scattering or expanding gas) rather than through optically thin ionised channel, which seems to be the case for low-redshift leakers (Kerutt et al. Reference Kerutt2024).
We do not expect LAEs in our sample to be strong LyC leakers. Hence, we simply assume a fiducial value of LyC escape
![]() $f^{\mathrm{LyC}}_{\mathrm{esc}} = 5$
% for our sources throughout the analysis. The ionising photon production efficiency is defined as the ratio of
$f^{\mathrm{LyC}}_{\mathrm{esc}} = 5$
% for our sources throughout the analysis. The ionising photon production efficiency is defined as the ratio of
![]() $Q_{\mathrm{ion}}$
and intrinsic UV luminosity density (
$Q_{\mathrm{ion}}$
and intrinsic UV luminosity density (
![]() $L_{\mathrm{UV},\nu}$
) (Matthee et al. Reference Matthee2017b) :
$L_{\mathrm{UV},\nu}$
) (Matthee et al. Reference Matthee2017b) :
We obtain
![]() $L_{\mathrm{UV},\nu}$
from
$L_{\mathrm{UV},\nu}$
from
![]() $\mathrm{M}_{\mathrm{UV}}$
, assuming negligible dust attenuation. We refer to Bouwens et al. (Reference Bouwens2016) for a discussion on the impact of dust attenuation on
$\mathrm{M}_{\mathrm{UV}}$
, assuming negligible dust attenuation. We refer to Bouwens et al. (Reference Bouwens2016) for a discussion on the impact of dust attenuation on
![]() $\xi_{\mathrm{ion}}$
. Our measured
$\xi_{\mathrm{ion}}$
. Our measured
![]() $\mathrm{M}_{\mathrm{UV}}$
values (see Table 1) indicate that these LAEs are UV-bright (
$\mathrm{M}_{\mathrm{UV}}$
values (see Table 1) indicate that these LAEs are UV-bright (
![]() $ -19.74 \leq \mathrm{M}_{\mathrm{UV}} \leq -23.27$
). The estimated
$ -19.74 \leq \mathrm{M}_{\mathrm{UV}} \leq -23.27$
). The estimated
![]() $\xi_{\mathrm{ion}}$
values are presented in Table 2. For the sources, which are detected in HSC, we find an average ionising photon production efficiency
$\xi_{\mathrm{ion}}$
values are presented in Table 2. For the sources, which are detected in HSC, we find an average ionising photon production efficiency
![]() $\mathrm{log}(\xi_{\mathrm{ion}}\, [\mathrm{Hz}\, \mathrm{erg}^{-1}]) = 25.51$
at
$\mathrm{log}(\xi_{\mathrm{ion}}\, [\mathrm{Hz}\, \mathrm{erg}^{-1}]) = 25.51$
at
![]() $z \lt 6$
, while
$z \lt 6$
, while
![]() $\mathrm{log}(\xi_{\mathrm{ion}}\, [\mathrm{Hz}\, \mathrm{erg}^{-1}]) = 25.74$
at
$\mathrm{log}(\xi_{\mathrm{ion}}\, [\mathrm{Hz}\, \mathrm{erg}^{-1}]) = 25.74$
at
![]() $z \gt 6$
. The slight evolution of
$z \gt 6$
. The slight evolution of
![]() $\xi_{\mathrm{ion}}$
with redshift is consistent with the previous studies (eg. Bouwens et al. Reference Bouwens2014; Endsley et al. Reference Endsley, Stark, Chevallard and Charlot2021b; Simmonds et al. Reference Simmonds2023; Tang et al. Reference Tang2023; Saxena et al. Reference Saxena2024). This aligns with the idea that younger galaxies may achieve higher ionising photon production efficiencies. However, the evolution is very mild which could suggest that the production and escape of ionising photons are governed by physical processes operating on much shorter timescales, such as intense star formation or supernova activity, which do not show a strong trend with redshift (Saxena et al. Reference Saxena2024). Further, we also note that some of the low-equivalent width (therefore, low
$\xi_{\mathrm{ion}}$
with redshift is consistent with the previous studies (eg. Bouwens et al. Reference Bouwens2014; Endsley et al. Reference Endsley, Stark, Chevallard and Charlot2021b; Simmonds et al. Reference Simmonds2023; Tang et al. Reference Tang2023; Saxena et al. Reference Saxena2024). This aligns with the idea that younger galaxies may achieve higher ionising photon production efficiencies. However, the evolution is very mild which could suggest that the production and escape of ionising photons are governed by physical processes operating on much shorter timescales, such as intense star formation or supernova activity, which do not show a strong trend with redshift (Saxena et al. Reference Saxena2024). Further, we also note that some of the low-equivalent width (therefore, low
![]() $f^{\mathrm{Ly}\alpha}_{\mathrm{esc}}$
) LAEs (
$f^{\mathrm{Ly}\alpha}_{\mathrm{esc}}$
) LAEs (
![]() $\mathrm{EW}_0 \lt 20$
Å; i.e, MAGPI1503111271, MAGPI1204117107, MAGPI1528094186, and MAGPI1522272275) show higher
$\mathrm{EW}_0 \lt 20$
Å; i.e, MAGPI1503111271, MAGPI1204117107, MAGPI1528094186, and MAGPI1522272275) show higher
![]() $\xi_{\mathrm{ion}}$
(see Table 2). Such a tentative anti-correlation between
$\xi_{\mathrm{ion}}$
(see Table 2). Such a tentative anti-correlation between
![]() $f^{\mathrm{Ly}\alpha}_{\mathrm{esc}}$
and
$f^{\mathrm{Ly}\alpha}_{\mathrm{esc}}$
and
![]() $\xi_{\mathrm{ion}}$
has been reported in a large sample of LAEs from JEMS and MUSE (see Simmonds et al. Reference Simmonds2023). This could indicate a time delay between production and escape of ionising photons in these galaxies (Katz et al. Reference Katz2020), which again may be linked to supernova activity.
$\xi_{\mathrm{ion}}$
has been reported in a large sample of LAEs from JEMS and MUSE (see Simmonds et al. Reference Simmonds2023). This could indicate a time delay between production and escape of ionising photons in these galaxies (Katz et al. Reference Katz2020), which again may be linked to supernova activity.
For constant Ly
![]() $\alpha$
luminosity and
$\alpha$
luminosity and
![]() $f^{\mathrm{LyC}}_{\mathrm{esc}}$
, hence for a constant production rate
$f^{\mathrm{LyC}}_{\mathrm{esc}}$
, hence for a constant production rate
![]() $Q_{\mathrm{ion}}$
, Equation (3) can be solved analytically to obtain an expression of bubble sizes that can be produced by the LAE on its own. For instance, neglecting the accelerated expansion due to Hubble flow and for luminous sources at
$Q_{\mathrm{ion}}$
, Equation (3) can be solved analytically to obtain an expression of bubble sizes that can be produced by the LAE on its own. For instance, neglecting the accelerated expansion due to Hubble flow and for luminous sources at
![]() $z \lesssim 8$
, when the recombination rate is relatively low, second term of Equation (3) dominates and we get an expression for bubble radius (Cen & Haiman Reference Cen and Haiman2000):
$z \lesssim 8$
, when the recombination rate is relatively low, second term of Equation (3) dominates and we get an expression for bubble radius (Cen & Haiman Reference Cen and Haiman2000):
 \begin{align} R_{\mathrm{B}} \approx \left(\frac{3\, Q_{\mathrm{ion}}\,f^{\mathrm{LyC}}_{\mathrm{esc}}\, t_{\mathrm{age}} }{4\pi\,n_{\mathrm{H}}(z)}\right)^{1/3}\end{align}
\begin{align} R_{\mathrm{B}} \approx \left(\frac{3\, Q_{\mathrm{ion}}\,f^{\mathrm{LyC}}_{\mathrm{esc}}\, t_{\mathrm{age}} }{4\pi\,n_{\mathrm{H}}(z)}\right)^{1/3}\end{align}
where
![]() $t_{\mathrm{age}}$
is the time since the ionising source has switched on. For these estimates, we assume a fiducial value of
$t_{\mathrm{age}}$
is the time since the ionising source has switched on. For these estimates, we assume a fiducial value of
![]() $t_{\mathrm{age}} = 100$
Myr (a reasonable amount of time for
$t_{\mathrm{age}} = 100$
Myr (a reasonable amount of time for
![]() $f^{\mathrm{LyC}}_{\mathrm{esc}} = 5$
%; see Witstok et al. Reference Witstok2024; Whitler et al. Reference Whitler2024) for all the LAEs. Recent studies note that the inferred bubble size does not strongly depend on small deviations in LyC escape fraction and age (see, Witstok et al. Reference Witstok2024; Torralba-Torregrosa et al. Reference Torralba-Torregrosa2024). For one luminous LAE (ID: MAGPI2310222098), we study the evolution of bubble size as a function of
$f^{\mathrm{LyC}}_{\mathrm{esc}} = 5$
%; see Witstok et al. Reference Witstok2024; Whitler et al. Reference Whitler2024) for all the LAEs. Recent studies note that the inferred bubble size does not strongly depend on small deviations in LyC escape fraction and age (see, Witstok et al. Reference Witstok2024; Torralba-Torregrosa et al. Reference Torralba-Torregrosa2024). For one luminous LAE (ID: MAGPI2310222098), we study the evolution of bubble size as a function of
![]() $t_{\mathrm{age}}$
for different values of the LyC escape fraction (see, Fig. 3). For a constant Ly
$t_{\mathrm{age}}$
for different values of the LyC escape fraction (see, Fig. 3). For a constant Ly
![]() $\alpha$
escape fraction (
$\alpha$
escape fraction (
![]() $f^{\mathrm{Ly}\alpha}_{\mathrm{esc}} \approx 24$
%), we find that this LAE is capable of ionising a bubble of radius
$f^{\mathrm{Ly}\alpha}_{\mathrm{esc}} \approx 24$
%), we find that this LAE is capable of ionising a bubble of radius
![]() $R_{\mathrm{B}} \sim 0.59$
pMpc in
$R_{\mathrm{B}} \sim 0.59$
pMpc in
![]() $t_{\mathrm{age}} = 100$
Myr for a LyC escape of
$t_{\mathrm{age}} = 100$
Myr for a LyC escape of
![]() $f^{\mathrm{LyC}}_{\mathrm{esc}} = 5$
% while it takes
$f^{\mathrm{LyC}}_{\mathrm{esc}} = 5$
% while it takes
![]() $t_{\mathrm{age}} = 50\, (30)$
Myr to ionise the same bubble size, when
$t_{\mathrm{age}} = 50\, (30)$
Myr to ionise the same bubble size, when
![]() $f^{\mathrm{LyC}}_{\mathrm{esc}} = 10\, (15)$
%. We also note that
$f^{\mathrm{LyC}}_{\mathrm{esc}} = 10\, (15)$
%. We also note that
![]() $t_{\mathrm{age}}$
depends on the actual time duration of constant star-formation within the galaxy, which is fundamentally bounded to
$t_{\mathrm{age}}$
depends on the actual time duration of constant star-formation within the galaxy, which is fundamentally bounded to
![]() $\lesssim+200$
Myr at this epoch (see, Tacchella et al. Reference Tacchella, Bose, Conroy, Eisenstein and Johnson2018; Whitler et al. Reference Whitler2023).
$\lesssim+200$
Myr at this epoch (see, Tacchella et al. Reference Tacchella, Bose, Conroy, Eisenstein and Johnson2018; Whitler et al. Reference Whitler2023).
Based on the assumptions mentioned above (
![]() $t_{\mathrm{age}} = 100$
Myr and
$t_{\mathrm{age}} = 100$
Myr and
![]() $f^{\mathrm{LyC}}_{\mathrm{esc}} = 5$
%), we find that each of our LAEs reside in ionised bubbles of radii
$f^{\mathrm{LyC}}_{\mathrm{esc}} = 5$
%), we find that each of our LAEs reside in ionised bubbles of radii
![]() $R_\mathrm{B} = 0.31 - 0.86$
pMpc (see, Table 2). From Equations (4) and (6), we note that bubble radius scales with the Ly
$R_\mathrm{B} = 0.31 - 0.86$
pMpc (see, Table 2). From Equations (4) and (6), we note that bubble radius scales with the Ly
![]() $\alpha$
luminosity as
$\alpha$
luminosity as
![]() $R_\mathrm{B} \propto L^{1/3}_{\mathrm{Ly}\alpha}$
. Modeling of Ly
$R_\mathrm{B} \propto L^{1/3}_{\mathrm{Ly}\alpha}$
. Modeling of Ly
![]() $\alpha$
emission and transmission during the EoR also predicts that Ly
$\alpha$
emission and transmission during the EoR also predicts that Ly
![]() $\alpha$
luminosity increases with
$\alpha$
luminosity increases with
![]() $R_{\mathrm{B}}$
due to higher IGM transmission for large ionised bubbles (see, Yajima et al. Reference Yajima, Sugimura and Hasegawa2018). We find a linear correlation between bubble radii and Ly
$R_{\mathrm{B}}$
due to higher IGM transmission for large ionised bubbles (see, Yajima et al. Reference Yajima, Sugimura and Hasegawa2018). We find a linear correlation between bubble radii and Ly
![]() $\alpha$
line widths (see Fig. 4) with high statistical significance (Spearman correlation coefficient
$\alpha$
line widths (see Fig. 4) with high statistical significance (Spearman correlation coefficient
![]() $= 0.53$
and p-value
$= 0.53$
and p-value
![]() $= 0.006$
). This trend is more prominent in LAEs at
$= 0.006$
). This trend is more prominent in LAEs at
![]() $z \gt 6$
, which is expected given the correlation between Ly
$z \gt 6$
, which is expected given the correlation between Ly
![]() $\alpha$
luminosity and line width at
$\alpha$
luminosity and line width at
![]() $z \gt 6$
, as discussed in the previous section. This again supports the fact that broadening of Ly
$z \gt 6$
, as discussed in the previous section. This again supports the fact that broadening of Ly
![]() $\alpha$
lines at
$\alpha$
lines at
![]() $z \gt 6$
is due to large ionised bubble which are created around them, allowing most of the Ly
$z \gt 6$
is due to large ionised bubble which are created around them, allowing most of the Ly
![]() $\alpha$
photons to come out of that the galaxy without suffering from much scattering in the IGM (Songaila et al. Reference Songaila, Barger, Cowie, Hu and Taylor2022; Songaila et al. Reference Songaila, Cowie, Barger, Hu and Taylor2024).
$\alpha$
photons to come out of that the galaxy without suffering from much scattering in the IGM (Songaila et al. Reference Songaila, Barger, Cowie, Hu and Taylor2022; Songaila et al. Reference Songaila, Cowie, Barger, Hu and Taylor2024).
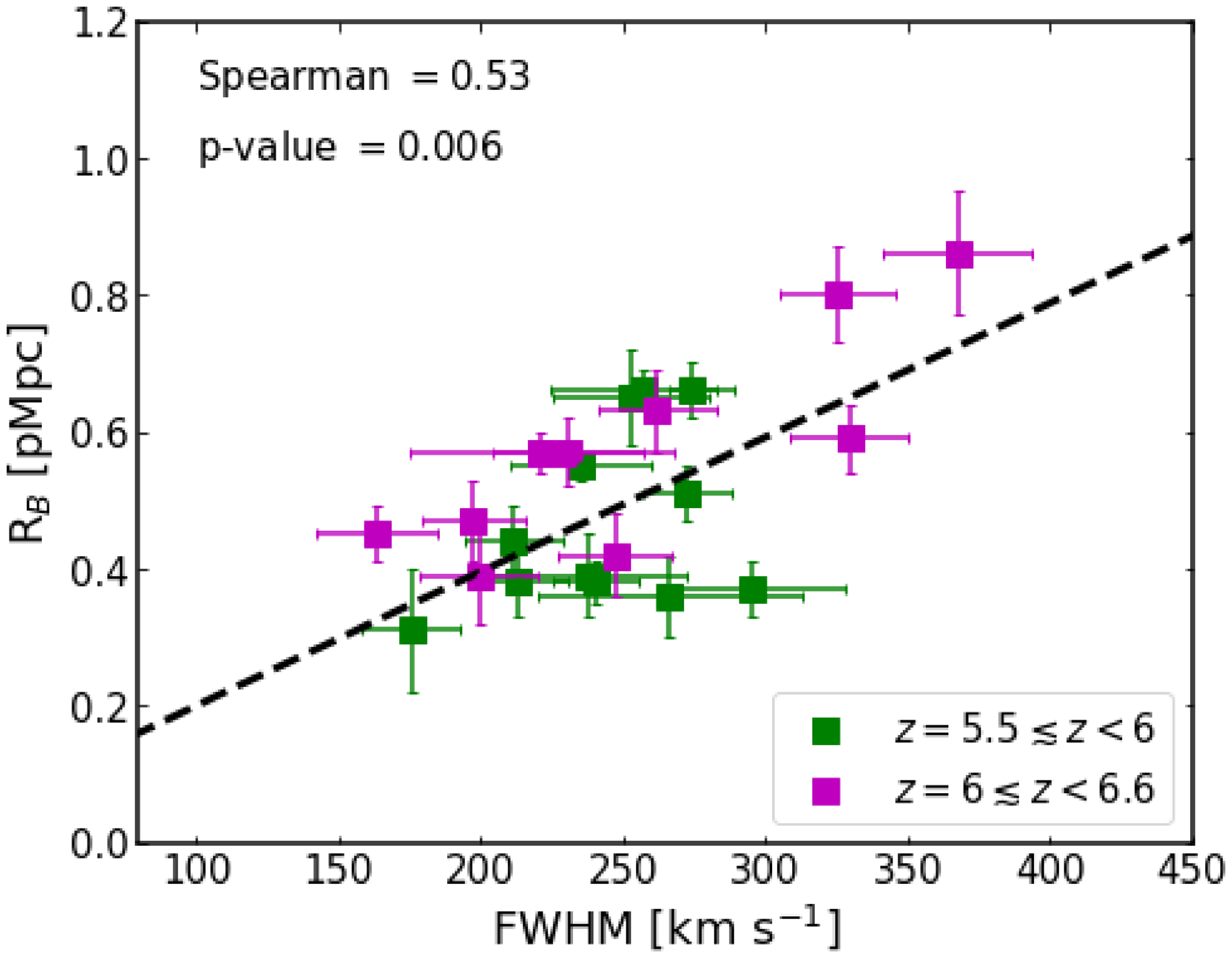
Figure 4. Evolution of the bubble radius as a function of Ly
![]() $\alpha$
line width for our 22 MAGPI LAEs. LAEs at
$\alpha$
line width for our 22 MAGPI LAEs. LAEs at
![]() $5.5 \lesssim z \lt 6$
are highlighted in green squares whereas LAEs at
$5.5 \lesssim z \lt 6$
are highlighted in green squares whereas LAEs at
![]() $z \gt 6$
are shown in purple squares. Significance of the plot (Spearman correlation coefficient and p-value) are shown in the top left corner.
$z \gt 6$
are shown in purple squares. Significance of the plot (Spearman correlation coefficient and p-value) are shown in the top left corner.
At high redshifts, Ly
![]() $\alpha$
lines are usually redshifted with respect to systemic velocity due to strong outflows, which facilitates the transmission of Ly
$\alpha$
lines are usually redshifted with respect to systemic velocity due to strong outflows, which facilitates the transmission of Ly
![]() $\alpha$
photons through IGM (Dijkstra, Mesinger, & Wyithe Reference Dijkstra, Mesinger and Wyithe2011). The velocity offset of the red peak has been used to place lower limits on the bubble sizes required for IGM transmission (Mason & Gronke Reference Mason and Gronke2020; Witstok et al. Reference Witstok2024). Considering a patchy reionisation scenario, where a galaxy is typically surrounded by a completely neutral IGM, it is found that Ly
$\alpha$
photons through IGM (Dijkstra, Mesinger, & Wyithe Reference Dijkstra, Mesinger and Wyithe2011). The velocity offset of the red peak has been used to place lower limits on the bubble sizes required for IGM transmission (Mason & Gronke Reference Mason and Gronke2020; Witstok et al. Reference Witstok2024). Considering a patchy reionisation scenario, where a galaxy is typically surrounded by a completely neutral IGM, it is found that Ly
![]() $\alpha$
can be detected at a high velocity offset of
$\alpha$
can be detected at a high velocity offset of
![]() $\gtrsim+300 \, \mathrm{km}\, \mathrm{s}^{-1}$
when the galaxy is situated in a ionised region of radius
$\gtrsim+300 \, \mathrm{km}\, \mathrm{s}^{-1}$
when the galaxy is situated in a ionised region of radius
![]() $R_{\mathrm{B}} \gtrsim 0.1$
pMpc (see Mason & Gronke Reference Mason and Gronke2020; Umeda et al. Reference Umeda2023). A Bayesian approach of modeling intrinsic Ly
$R_{\mathrm{B}} \gtrsim 0.1$
pMpc (see Mason & Gronke Reference Mason and Gronke2020; Umeda et al. Reference Umeda2023). A Bayesian approach of modeling intrinsic Ly
![]() $\alpha$
profiles has predicted the size of ionised regions to be
$\alpha$
profiles has predicted the size of ionised regions to be
![]() $R_{\mathrm{B}} = 0.5 - 2.5$
pMpc at
$R_{\mathrm{B}} = 0.5 - 2.5$
pMpc at
![]() $z \gt 6$
(Hayes & Scarlata Reference Hayes and Scarlata2023). Witstok et al. (Reference Witstok2024) find that LAEs with relatively low Ly
$z \gt 6$
(Hayes & Scarlata Reference Hayes and Scarlata2023). Witstok et al. (Reference Witstok2024) find that LAEs with relatively low Ly
![]() $\alpha$
velocity offset (
$\alpha$
velocity offset (
![]() $\lesssim+300 \, \mathrm{km}\, \mathrm{s}^{-1}$
) with moderately high escape fraction can represent ionised regions of sizes
$\lesssim+300 \, \mathrm{km}\, \mathrm{s}^{-1}$
) with moderately high escape fraction can represent ionised regions of sizes
![]() $R_{\mathrm{B}} = 0.1 - 1$
pMpc. Further, several attempts have been made to put constraints on the size of ionised regions that allow blue peak of Ly
$R_{\mathrm{B}} = 0.1 - 1$
pMpc. Further, several attempts have been made to put constraints on the size of ionised regions that allow blue peak of Ly
![]() $\alpha$
to be detected at
$\alpha$
to be detected at
![]() $z \gt 6$
, where it is found that the blue peak can be detected if the source galaxy resides in a highly ionised region (
$z \gt 6$
, where it is found that the blue peak can be detected if the source galaxy resides in a highly ionised region (
![]() $x_{\mathrm{HI}} \gt 10^{-5}$
) of radius
$x_{\mathrm{HI}} \gt 10^{-5}$
) of radius
![]() $R_{\mathrm{B}} \gtrsim 0.5 $
pMpc (see, Mason & Gronke Reference Mason and Gronke2020; Torralba-Torregrosa et al. Reference Torralba-Torregrosa2024). We note that, while some of our LAEs show larger bubble sizes, we cannot always anticipate seeing a blue-peak emission from them, as these photons might be heavily absorbed by neutral hydrogen in the circumgalactic medium (CGM; Henry et al. Reference Henry, Scarlata, Martin and Erb2015; Gazagnes et al. Reference Gazagnes, Chisholm, Schaerer, Verhamme and Izotov2020; Endsley & Stark Reference Endsley and Stark2022).
$R_{\mathrm{B}} \gtrsim 0.5 $
pMpc (see, Mason & Gronke Reference Mason and Gronke2020; Torralba-Torregrosa et al. Reference Torralba-Torregrosa2024). We note that, while some of our LAEs show larger bubble sizes, we cannot always anticipate seeing a blue-peak emission from them, as these photons might be heavily absorbed by neutral hydrogen in the circumgalactic medium (CGM; Henry et al. Reference Henry, Scarlata, Martin and Erb2015; Gazagnes et al. Reference Gazagnes, Chisholm, Schaerer, Verhamme and Izotov2020; Endsley & Stark Reference Endsley and Stark2022).
Ly
![]() $\alpha$
radiative transfer modeling suggests strong correlation between Ly
$\alpha$
radiative transfer modeling suggests strong correlation between Ly
![]() $\alpha$
velocity offset and
$\alpha$
velocity offset and
![]() $N_{\mathrm{HI}}$
(Verhamme et al. Reference Verhamme, Orlitová, Schaerer and Hayes2015). As
$N_{\mathrm{HI}}$
(Verhamme et al. Reference Verhamme, Orlitová, Schaerer and Hayes2015). As
![]() $N_{\mathrm{HI}}$
increases the peak velocity shifts farther from the systemic velocity. Further, shell model predicts that for a low
$N_{\mathrm{HI}}$
increases the peak velocity shifts farther from the systemic velocity. Further, shell model predicts that for a low
![]() $N_{\mathrm{HI}}$
and high outflow velocity, most of the Ly
$N_{\mathrm{HI}}$
and high outflow velocity, most of the Ly
![]() $\alpha$
photons can directly escape at the line centre frequency (Yajima et al. Reference Yajima, Sugimura and Hasegawa2018). In addition, line width becomes narrower when
$\alpha$
photons can directly escape at the line centre frequency (Yajima et al. Reference Yajima, Sugimura and Hasegawa2018). In addition, line width becomes narrower when
![]() $N_{\mathrm{HI}}$
decreases. This is expected as low
$N_{\mathrm{HI}}$
decreases. This is expected as low
![]() $N_{\mathrm{HI}}$
shifts the peak to shorter wavelengths, where Ly
$N_{\mathrm{HI}}$
shifts the peak to shorter wavelengths, where Ly
![]() $\alpha$
flux is significantly reduced due to IGM scattering. While IGM radiative transfer establishes a typical correlation between the line width and velocity offset of Ly
$\alpha$
flux is significantly reduced due to IGM scattering. While IGM radiative transfer establishes a typical correlation between the line width and velocity offset of Ly
![]() $\alpha$
red peaks (e.g. Neufeld Reference Neufeld1990; Verhamme et al. Reference Verhamme2018; Li & Gronke Reference Li and Gronke2022), this trend is expected to change at high redshifts due to IGM absorption. Ignoring such complicated radiative transfer effects at high redshifts, we can simply assume that Ly
$\alpha$
red peaks (e.g. Neufeld Reference Neufeld1990; Verhamme et al. Reference Verhamme2018; Li & Gronke Reference Li and Gronke2022), this trend is expected to change at high redshifts due to IGM absorption. Ignoring such complicated radiative transfer effects at high redshifts, we can simply assume that Ly
![]() $\alpha$
line width is positively correlated with
$\alpha$
line width is positively correlated with
![]() $N_{\mathrm{HI}}$
as
$N_{\mathrm{HI}}$
as
![]() $\mathrm{FWHM} \simeq 320 \left(\frac{N_{\mathrm{HI}}}{10^{20} \mathrm{cm}^{-2}}\right)^{1/3}$
(Dijkstra Reference Dijkstra2017; Li & Gronke Reference Li and Gronke2022) for a static shell with temperature
$\mathrm{FWHM} \simeq 320 \left(\frac{N_{\mathrm{HI}}}{10^{20} \mathrm{cm}^{-2}}\right)^{1/3}$
(Dijkstra Reference Dijkstra2017; Li & Gronke Reference Li and Gronke2022) for a static shell with temperature
![]() ${T}_{\mathrm{eff}} = 10^4$
K. This translates to a column density
${T}_{\mathrm{eff}} = 10^4$
K. This translates to a column density
![]() $\mathrm{log}(N_{\mathrm{HI}}) \sim 20.18 \, \mathrm{cm}^{-2} $
for the highest FWHM LAE in our sample (i.e. MAGPI1204117107 at
$\mathrm{log}(N_{\mathrm{HI}}) \sim 20.18 \, \mathrm{cm}^{-2} $
for the highest FWHM LAE in our sample (i.e. MAGPI1204117107 at
![]() $z = 6.046$
). Further, using the correlation between velocity offset and
$z = 6.046$
). Further, using the correlation between velocity offset and
![]() $\mathrm{log}(N_{\mathrm{HI}})$
(which is approximated by a second order polynomial, see Fig. 2 of Verhamme et al. Reference Verhamme, Orlitová, Schaerer and Hayes2015), we expect this line to be at an offset of
$\mathrm{log}(N_{\mathrm{HI}})$
(which is approximated by a second order polynomial, see Fig. 2 of Verhamme et al. Reference Verhamme, Orlitová, Schaerer and Hayes2015), we expect this line to be at an offset of
![]() $300 \, \mathrm{km}\, \mathrm{s}^{-1}$
. We follow the IGM transmission model of Witstok et al. (Reference Witstok2024) and find that this LAE can have
$300 \, \mathrm{km}\, \mathrm{s}^{-1}$
. We follow the IGM transmission model of Witstok et al. (Reference Witstok2024) and find that this LAE can have
![]() $ \gt $
30% IGM transmission if it resides inside a bubble of radius
$ \gt $
30% IGM transmission if it resides inside a bubble of radius
![]() $R_{B} = 0.86$
pMpc. This estimation is in agreement with the findings of Endsley et al. (Reference Endsley2022), where they discover boosted Ly
$R_{B} = 0.86$
pMpc. This estimation is in agreement with the findings of Endsley et al. (Reference Endsley2022), where they discover boosted Ly
![]() $\alpha$
transmission in LAEs with large velocity offsets and broad line widths. On the other hand, MAGPI2310245276 at
$\alpha$
transmission in LAEs with large velocity offsets and broad line widths. On the other hand, MAGPI2310245276 at
![]() $z= 6.039$
(FWHM
$z= 6.039$
(FWHM
![]() $= 199.64 \, \mathrm{km}\, \mathrm{s}^{-1}$
) can only transmit
$= 199.64 \, \mathrm{km}\, \mathrm{s}^{-1}$
) can only transmit
![]() $ \lt $
10% of Ly
$ \lt $
10% of Ly
![]() $\alpha$
photons if it resides in
$\alpha$
photons if it resides in
![]() $R_{B} = 0.39$
pMpc bubble. However, it is also possible that for a very low velocity offset (
$R_{B} = 0.39$
pMpc bubble. However, it is also possible that for a very low velocity offset (
![]() $ \lt +200 \, \mathrm{km}\, \mathrm{s}^{-1} $
), a sufficiently large (
$ \lt +200 \, \mathrm{km}\, \mathrm{s}^{-1} $
), a sufficiently large (
![]() $R_{B} \gt 1.5$
pMpc) bubble will be able to transmit
$R_{B} \gt 1.5$
pMpc) bubble will be able to transmit
![]() $ \gt +60$
% of Ly
$ \gt +60$
% of Ly
![]() $\alpha$
photons (see, Fig. 3 of Witstok et al. Reference Witstok2024) by reducing the scattering effect, which can increase the observed Ly
$\alpha$
photons (see, Fig. 3 of Witstok et al. Reference Witstok2024) by reducing the scattering effect, which can increase the observed Ly
![]() $\alpha$
luminosity and may allow some photons to escape on the bluer side. A better understanding of
$\alpha$
luminosity and may allow some photons to escape on the bluer side. A better understanding of
![]() $N_{\mathrm{HI}}$
– FWHM – velocity offset relation at
$N_{\mathrm{HI}}$
– FWHM – velocity offset relation at
![]() $z \gt 6$
will require efficient radiative transfer modeling of these high-redshift LAEs.
$z \gt 6$
will require efficient radiative transfer modeling of these high-redshift LAEs.
Our analysis suggests that galaxies with broader Ly
![]() $\alpha$
emission lines are generally located within larger ionised bubbles. However, we caution that this may not always hold true. For instance, UV-bright galaxies in the reionisation era may exhibit wider Ly
$\alpha$
emission lines are generally located within larger ionised bubbles. However, we caution that this may not always hold true. For instance, UV-bright galaxies in the reionisation era may exhibit wider Ly
![]() $\alpha$
line profiles if they have more H i present in their CGM, resulting in more scattering of Ly
$\alpha$
line profiles if they have more H i present in their CGM, resulting in more scattering of Ly
![]() $\alpha$
photons (see, Tang et al. Reference Tang2023). Moreover, UV-bright galaxies are found to display larger Ly
$\alpha$
photons (see, Tang et al. Reference Tang2023). Moreover, UV-bright galaxies are found to display larger Ly
![]() $\alpha$
velocity offsets (e.g. Endsley et al. Reference Endsley2022; Valentino et al. Reference Valentino2022; Tang et al. Reference Tang2023; Witten et al. Reference Witten, Laporte and Katz2023). In such cases, most of the Ly
$\alpha$
velocity offsets (e.g. Endsley et al. Reference Endsley2022; Valentino et al. Reference Valentino2022; Tang et al. Reference Tang2023; Witten et al. Reference Witten, Laporte and Katz2023). In such cases, most of the Ly
![]() $\alpha$
photons emerge at relatively high velocities, experiencing minimal attenuation by the neutral IGM (see, Mason & Gronke Reference Mason and Gronke2020). Visibility of Ly
$\alpha$
photons emerge at relatively high velocities, experiencing minimal attenuation by the neutral IGM (see, Mason & Gronke Reference Mason and Gronke2020). Visibility of Ly
![]() $\alpha$
during reionisation can also be enhanced by efficient ionising photon production due to hard ionising field (e.g. Mainali et al. Reference Mainali2018; Tang et al. Reference Tang2023), or if Ly
$\alpha$
during reionisation can also be enhanced by efficient ionising photon production due to hard ionising field (e.g. Mainali et al. Reference Mainali2018; Tang et al. Reference Tang2023), or if Ly
![]() $\alpha$
is produced in gas clumps moving with large peculiar motions, leading to intrinsically broad Ly
$\alpha$
is produced in gas clumps moving with large peculiar motions, leading to intrinsically broad Ly
![]() $\alpha$
profile (e.g. Endsley et al. Reference Endsley2022). Therefore, wide Ly
$\alpha$
profile (e.g. Endsley et al. Reference Endsley2022). Therefore, wide Ly
![]() $\alpha$
lines from LAEs can survive even in moderate-sized ionised bubbles (e.g. Endsley et al. Reference Endsley2022). Future observations of Ly
$\alpha$
lines from LAEs can survive even in moderate-sized ionised bubbles (e.g. Endsley et al. Reference Endsley2022). Future observations of Ly
![]() $\alpha$
in both UV-bright and faint galaxies during the reionisation era will provide more precise constraints on bubble sizes and the influence of the IGM on Ly
$\alpha$
in both UV-bright and faint galaxies during the reionisation era will provide more precise constraints on bubble sizes and the influence of the IGM on Ly
![]() $\alpha$
transmission.
$\alpha$
transmission.
Figure 5.
Left panel: Synthetic MUSE Ly
![]() $\alpha$
narrow band (NB) image collapsed for wavelengths within
$\alpha$
narrow band (NB) image collapsed for wavelengths within
![]() $8\,550$
–
$8\,550$
–
![]() $8\,590$
Å, showing two LAEs with MAGPI IDs 1529106057 and 1529110045 at
$8\,590$
Å, showing two LAEs with MAGPI IDs 1529106057 and 1529110045 at
![]() $z = 6.046$
, separated by a physical distance of
$z = 6.046$
, separated by a physical distance of
![]() $15.92$
kpc. Contours are shown as black dashed lines at the 2 and
$15.92$
kpc. Contours are shown as black dashed lines at the 2 and
![]() $4 \sigma$
significance levels. Right panel: Three-dimensional visualisation of the size of ionised bubbles created by them along the line of sight. Bubbles are shown in wire-frame spheres centred on each LAE. The centre of the LAE MAGPI1529110045 is at the origin of this 3D plot.
$4 \sigma$
significance levels. Right panel: Three-dimensional visualisation of the size of ionised bubbles created by them along the line of sight. Bubbles are shown in wire-frame spheres centred on each LAE. The centre of the LAE MAGPI1529110045 is at the origin of this 3D plot.
4.3 Closely separated LAE pair: Overlapping bubbles?
We find two closely separated LAE pairs. There are two LAEs in MAGPI2310 field (MAGPI IDs: 2310245276 and 2310222098) at
![]() $z = 6.039$
and
$z = 6.039$
and
![]() $z = 6.1485$
, respectively, are located 36′′ apart on the sky, which corresponds to a physical distance of 203 kpc. Their separation along the line of sight is
$z = 6.1485$
, respectively, are located 36′′ apart on the sky, which corresponds to a physical distance of 203 kpc. Their separation along the line of sight is
![]() $6.32$
pMpc. As a result, the estimated radii of their bubbles indicate that these bubbles do not overlap. We also find two LAEs at
$6.32$
pMpc. As a result, the estimated radii of their bubbles indicate that these bubbles do not overlap. We also find two LAEs at
![]() $z = 6.046$
in MAGPI1529 field (MAGPI IDs: 1529106057 and 1529110045), whose redshifts differ only by
$z = 6.046$
in MAGPI1529 field (MAGPI IDs: 1529106057 and 1529110045), whose redshifts differ only by
![]() $0.0002$
, which corresponds to a velocity shift of only
$0.0002$
, which corresponds to a velocity shift of only
![]() $ 61 \, \mathrm{km} \, \mathrm{s}^{-1}$
. They are located only 3′′ apart on the sky (see Fig. 5), translating to a projected physical separation of
$ 61 \, \mathrm{km} \, \mathrm{s}^{-1}$
. They are located only 3′′ apart on the sky (see Fig. 5), translating to a projected physical separation of
![]() $15.92 \,$
kpc. The estimated bubble radii for them suggest that their bubbles overlap and they likely sit inside a single large ionised region (see Fig. 5, right panel).
$15.92 \,$
kpc. The estimated bubble radii for them suggest that their bubbles overlap and they likely sit inside a single large ionised region (see Fig. 5, right panel).
Closely separated LAEs have been previously observed in the reionisation era (see, Castellano et al. Reference Castellano2016; Hu et al. Reference Hu2017; Tilvi et al. Reference Tilvi2020; Endsley et al. Reference Endsley2021a; Endsley & Stark Reference Endsley and Stark2022; Chen et al. Reference Chen2024; Witstok et al. Reference Witstok2024). Many of these LAEs are found to reside in overdense regions populated by fainter galaxies (e.g. Castellano et al. Reference Castellano2016; Castellano et al. Reference Castellano2018; Chen et al. Reference Chen2024; Witstok et al. Reference Witstok2024; Whitler et al. Reference Whitler2024). On the other hand, Endsley & Stark (Reference Endsley and Stark2022) detect many UV-bright galaxies making an overdense region around three closely separated Lyman-break galaxies at
![]() $z \sim 6.8$
. Closely separated LAEs in overdense regions can cause bubble overlap, which results in the formation of giant ionised bubbles, allowing a boosted transmission of Ly
$z \sim 6.8$
. Closely separated LAEs in overdense regions can cause bubble overlap, which results in the formation of giant ionised bubbles, allowing a boosted transmission of Ly
![]() $\alpha$
through the neutral IGM (Mason et al. Reference Mason2018; Jung et al. Reference Jung2022a). With our current data, we cannot yet fully characterise the extent of the ionised regions surrounding the closely separated LAEs in our sample. Future spectroscopic follow-up of these LAEs, as well as spectroscopy and deep photometry focusing on fainter galaxies in the surrounding area are necessary to place further constraints on the size of the ionised bubbles in those regions. Further, we note that our LAE pair at
$\alpha$
through the neutral IGM (Mason et al. Reference Mason2018; Jung et al. Reference Jung2022a). With our current data, we cannot yet fully characterise the extent of the ionised regions surrounding the closely separated LAEs in our sample. Future spectroscopic follow-up of these LAEs, as well as spectroscopy and deep photometry focusing on fainter galaxies in the surrounding area are necessary to place further constraints on the size of the ionised bubbles in those regions. Further, we note that our LAE pair at
![]() $z = 6.046$
is UV-bright (
$z = 6.046$
is UV-bright (
![]() $\mathrm{M}_{\mathrm{UV}} \sim -21$
), similar to that of the closely separated LAEs discussed in Endsley et al. (Reference Endsley2021a), potentially indicating that UV-bright galaxies in overdense regions enhance Ly
$\mathrm{M}_{\mathrm{UV}} \sim -21$
), similar to that of the closely separated LAEs discussed in Endsley et al. (Reference Endsley2021a), potentially indicating that UV-bright galaxies in overdense regions enhance Ly
![]() $\alpha$
transmission (Endsley et al. Reference Endsley2021a; Endsley & Stark Reference Endsley and Stark2022). Reionisation simulation has also predicted that reionisation is more advanced in high-density regions compared to those that are isolated, indicating that LAE clustering could lead to Ly
$\alpha$
transmission (Endsley et al. Reference Endsley2021a; Endsley & Stark Reference Endsley and Stark2022). Reionisation simulation has also predicted that reionisation is more advanced in high-density regions compared to those that are isolated, indicating that LAE clustering could lead to Ly
![]() $\alpha$
emission that is less-attenuated by the IGM (Qin et al. Reference Qin2022; Lu et al. Reference Lu2024). Considering different models for the internal velocity structure of a galaxy (i.e. expanding shell or cloud), Yajima et al. (Reference Yajima, Sugimura and Hasegawa2018) find that the overlapping bubbles are likely to affect the outflow velocity. Further, LAE clustering during reionisation supports an accelerated reionisation scenario, suggesting that reionisation proceeds faster in regions around such galaxies (see, Endsley et al. Reference Endsley2021a).
$\alpha$
emission that is less-attenuated by the IGM (Qin et al. Reference Qin2022; Lu et al. Reference Lu2024). Considering different models for the internal velocity structure of a galaxy (i.e. expanding shell or cloud), Yajima et al. (Reference Yajima, Sugimura and Hasegawa2018) find that the overlapping bubbles are likely to affect the outflow velocity. Further, LAE clustering during reionisation supports an accelerated reionisation scenario, suggesting that reionisation proceeds faster in regions around such galaxies (see, Endsley et al. Reference Endsley2021a).
5. Summary and conclusions
We present spectroscopic properties of 22 newly discovered LAEs at the edge of reionisation era (
![]() $5.5 \lesssim z \lesssim 6.6$
), identified in the MAGPI data. For 17 of them covered in the HSC-Subaru Wide layer, we provide photometric magnitudes and
$5.5 \lesssim z \lesssim 6.6$
), identified in the MAGPI data. For 17 of them covered in the HSC-Subaru Wide layer, we provide photometric magnitudes and
![]() $2\sigma$
limits (for non-detections) of i, z, y broad-band filters. The HSC-y band magnitudes indicate that our LAEs are UV-bright, with rest-frame absolute UV magnitudes
$2\sigma$
limits (for non-detections) of i, z, y broad-band filters. The HSC-y band magnitudes indicate that our LAEs are UV-bright, with rest-frame absolute UV magnitudes
![]() $ -19.74 \leq \mathrm{M}_{\mathrm{UV}} \leq -23.27$
. We summarise our main findings as follows:
$ -19.74 \leq \mathrm{M}_{\mathrm{UV}} \leq -23.27$
. We summarise our main findings as follows:
(i) We observe that for
 $z \lt 6$
, the FWHM distribution of LAEs remains almost uniform with no significant change as luminosity increases. However, for
$z \lt 6$
, the FWHM distribution of LAEs remains almost uniform with no significant change as luminosity increases. However, for
 $z \gt 6$
, there is a noticeable increase in line width with increasing luminosity. This broadening at high redshifts suggests that high-luminosity LAEs at
$z \gt 6$
, there is a noticeable increase in line width with increasing luminosity. This broadening at high redshifts suggests that high-luminosity LAEs at
 $z \gt 6$
may be located in more highly ionised regions of the IGM, despite the fact that a more neutral IGM would typically narrow the line by scattering more Ly
$z \gt 6$
may be located in more highly ionised regions of the IGM, despite the fact that a more neutral IGM would typically narrow the line by scattering more Ly
 $\alpha$
photons.
$\alpha$
photons.(ii) We also find that some low-equivalent width (
 $\mathrm{EW}_0 \lt 20$
Å) LAEs exhibit higher ionising photon production efficiency. This suggests a possible anti-correlation between the Ly
$\mathrm{EW}_0 \lt 20$
Å) LAEs exhibit higher ionising photon production efficiency. This suggests a possible anti-correlation between the Ly
 $\alpha$
escape fraction and
$\alpha$
escape fraction and
 $\xi_{\mathrm{ion}}$
, as observed in other studies. This anti-correlation might indicate a time delay between the production and escape of ionising photons in these galaxies, potentially related to supernova activity.
$\xi_{\mathrm{ion}}$
, as observed in other studies. This anti-correlation might indicate a time delay between the production and escape of ionising photons in these galaxies, potentially related to supernova activity.(iii) Using the Ly
 $\alpha$
spectroscopic properties and based on some assumptions, we find that LAEs in our sample can ionise bubbles of size
$\alpha$
spectroscopic properties and based on some assumptions, we find that LAEs in our sample can ionise bubbles of size
 $R_{\mathrm{B}} = 0.31 - 0.86$
pMpc. The study also finds a significant linear correlation between bubble radii and Ly
$R_{\mathrm{B}} = 0.31 - 0.86$
pMpc. The study also finds a significant linear correlation between bubble radii and Ly
 $\alpha$
line widths. The correlation is particularly strong in LAEs at
$\alpha$
line widths. The correlation is particularly strong in LAEs at
 $z \gt 6$
, supporting the idea that the broadening of Ly
$z \gt 6$
, supporting the idea that the broadening of Ly
 $\alpha$
lines at these high redshifts is due to large ionised bubbles around those galaxies. Larger bubbles allow most of the Ly
$\alpha$
lines at these high redshifts is due to large ionised bubbles around those galaxies. Larger bubbles allow most of the Ly
 $\alpha$
photons to escape the galaxy with minimal scattering in the IGM. Based on simple model and assumptions, Ly
$\alpha$
photons to escape the galaxy with minimal scattering in the IGM. Based on simple model and assumptions, Ly
 $\alpha$
line width can be used to constrain the IGM transmission as well as bubble sizes. A narrow line width could indicate low H i column density, which will force Ly
$\alpha$
line width can be used to constrain the IGM transmission as well as bubble sizes. A narrow line width could indicate low H i column density, which will force Ly
 $\alpha$
photons to escape close to the line centre, where line flux is significantly reduced due to IGM scattering. However, this can be uncertain and depends on the complex radiative transfer of Ly
$\alpha$
photons to escape close to the line centre, where line flux is significantly reduced due to IGM scattering. However, this can be uncertain and depends on the complex radiative transfer of Ly
 $\alpha$
photons in the IGM and CGM. We also discuss that the enhanced visibility of Ly
$\alpha$
photons in the IGM and CGM. We also discuss that the enhanced visibility of Ly
 $\alpha$
could also be due to several other factors such as large velocity offset of Ly
$\alpha$
could also be due to several other factors such as large velocity offset of Ly
 $\alpha$
form systemic velocity, hardness of ionising field and due to large peculiar motions of gas clumps present in the galaxy. In such cases, wide Ly
$\alpha$
form systemic velocity, hardness of ionising field and due to large peculiar motions of gas clumps present in the galaxy. In such cases, wide Ly
 $\alpha$
can transmit through the neutral IGM even when the ionised bubble size is small.
$\alpha$
can transmit through the neutral IGM even when the ionised bubble size is small.(iv) Two closely separated LAE pairs are discovered in two MAGPI fields. One pair at
 $z = 6.046$
is just 3′′ apart on the sky, which corresponds to a physical separation of about
$z = 6.046$
is just 3′′ apart on the sky, which corresponds to a physical separation of about
 $15.92$
kpc. Their bubble radii indicate that they sit inside a single large ionised region. As far as we know, this is the pair of LAEs with the smallest separation ever identified in the reionisation era. Such overlap of ionised bubbles due to clustering of LAEs during reionisation increases the size of the ionised regions and enhances the transmission of Ly
$15.92$
kpc. Their bubble radii indicate that they sit inside a single large ionised region. As far as we know, this is the pair of LAEs with the smallest separation ever identified in the reionisation era. Such overlap of ionised bubbles due to clustering of LAEs during reionisation increases the size of the ionised regions and enhances the transmission of Ly
 $\alpha$
through the neutral IGM. Future spectroscopic and photometric follow-up of the area surrounding these LAEs will detect fainter galaxies, allowing for improved constraints on the size of the ionised bubbles in those regions.
$\alpha$
through the neutral IGM. Future spectroscopic and photometric follow-up of the area surrounding these LAEs will detect fainter galaxies, allowing for improved constraints on the size of the ionised bubbles in those regions.
This study shows how wide-area Ly
![]() $\alpha$
spectroscopy across a broad range of redshifts can aid in identifying and characterising ionised bubbles formed during reionisation. In the future, as new reionisation-era LAEs will be discovered in the upcoming MAGPI fields, it will be possible to place more precise constraints on the evolution of line width with luminosity. Additionally, spectroscopic follow-up using infrared spectroscopy will allow for the measurement of systemic redshifts, leading to more accurate determinations of bubble sizes.
$\alpha$
spectroscopy across a broad range of redshifts can aid in identifying and characterising ionised bubbles formed during reionisation. In the future, as new reionisation-era LAEs will be discovered in the upcoming MAGPI fields, it will be possible to place more precise constraints on the evolution of line width with luminosity. Additionally, spectroscopic follow-up using infrared spectroscopy will allow for the measurement of systemic redshifts, leading to more accurate determinations of bubble sizes.
Acknowledgement
We thank the anonymous referee for their constructive feedback that helped to improve this work. We wish to thank the ESO staff, and in particular the staff at Paranal Observatory, for carrying out the MAGPI observations. MAGPI targets were selected from GAMA. GAMA is a joint European-Australasian project based around a spectroscopic campaign using the Anglo-Australian Telescope. GAMA was funded by the STFC (UK), the ARC (Australia), the AAO, and the participating institutions. GAMA photometry is based on observations made with ESO Telescopes at the La Silla Paranal Observatory under programme ID 179.A-2004, ID 177.A-3016. The MAGPI team acknowledge support from the Australian Research Council Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D), through project number CE170100013.
The Hyper Suprime-Cam (HSC) collaboration includes the astronomical communities of Japan and Taiwan, and Princeton University. The HSC instrumentation and software were developed by the National Astronomical Observatory of Japan (NAOJ), the Kavli Institute for the Physics and Mathematics of the Universe (Kavli IPMU), the University of Tokyo, the High Energy Accelerator Research Organization (KEK), the Academia Sinica Institute for Astronomy and Astrophysics in Taiwan (ASIAA), and Princeton University. Funding was contributed by the FIRST program from Japanese Cabinet Office, the Ministry of Education, Culture, Sports, Science and Technology (MEXT), the Japan Society for the Promotion of Science (JSPS), Japan Science and Technology Agency (JST), the Toray Science Foundation, NAOJ, Kavli IPMU, KEK, ASIAA, and Princeton University.
This paper is based on data collected at the Subaru Telescope and retrieved from the HSC data archive system, which is operated by the Subaru Telescope and Astronomy Data Center (ADC) at NAOJ. Data analysis was in part carried out with the cooperation of Center for Computational Astrophysics (CfCA), NAOJ.
SGL acknowledge the financial support from the MICIU with funding from the European Union NextGenerationEU and Generalitat Valenciana in the call Programa de Planes Complementarios de I+D+i (PRTR 2022) Project (VAL-JPAS), reference ASFAE/2022/025. KEH acknowledges funding from the Australian Research Council (ARC) Discovery Project DP210101945. SMS acknowledges funding from the Australian Research Council (DE220100003). Parts of this research were conducted by the Australian Research Council Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D), through project number CE170100013. LMV acknowledges support by the German Academic Scholarship Foundation (Studienstiftung des deutschen Volkes) and the Marianne-Plehn-Program of the Elite Network of Bavaria.
Data availability statement
All MUSE data utilised in this work are publicly accessible through the ESO archive (http://archive.eso.org/cms.html). Data products such as fully reduced data cubes and emission line fits will be made available as part of an upcoming MAGPI team data release (Mendel et al. in prep; Battisti et al. in prep).
Appendix 1. Fitting Ly
 $\boldsymbol{\alpha}$
lines
$\boldsymbol{\alpha}$
lines
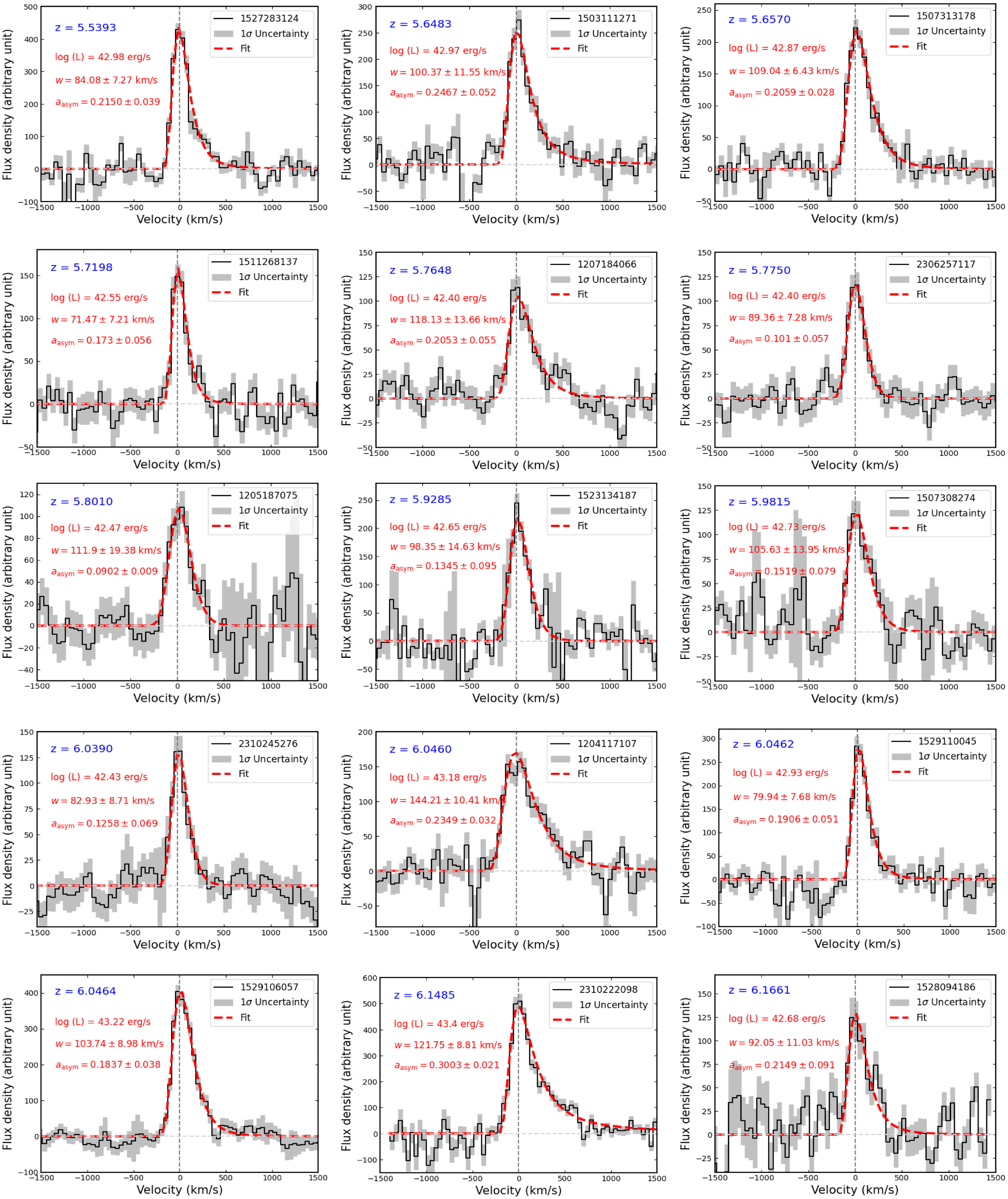
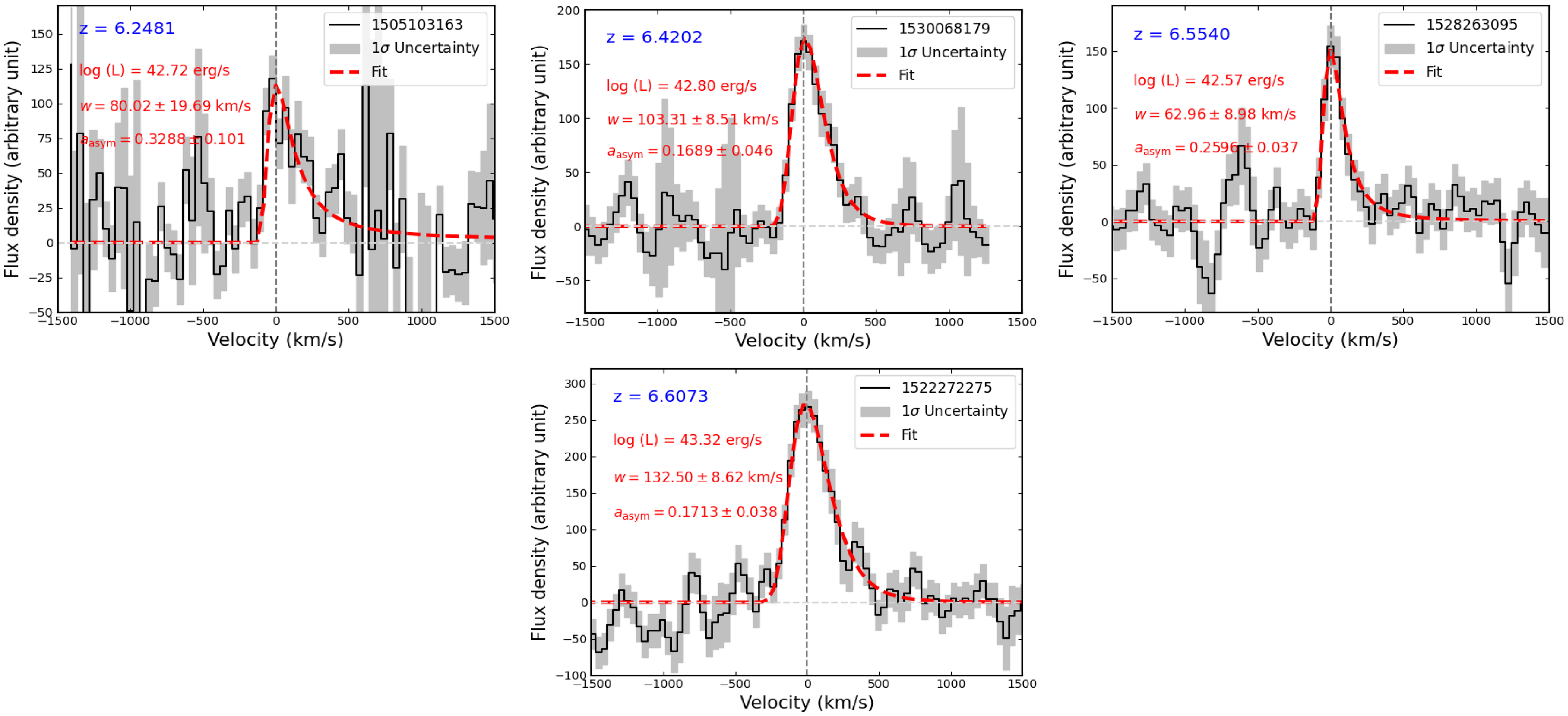
Figure A1. Shown are the velocity profiles of 22 LAEs at
![]() $5.5 \lesssim z \lesssim 6.6$
. 1D spectrum (solid black, named by corresponding MAGPI ID) and associated
$5.5 \lesssim z \lesssim 6.6$
. 1D spectrum (solid black, named by corresponding MAGPI ID) and associated
![]() $\pm 1 \sigma$
uncertainty on the flux density (grey shaded), along with the asymmetric Gaussian fit (dashed-red) to the spectrum for each LAE are presented in each panels. In each panel, luminosity, redshift and best-fit parameters such as w defining FWHM, and asymmetry parameter are given in the left corners.
$\pm 1 \sigma$
uncertainty on the flux density (grey shaded), along with the asymmetric Gaussian fit (dashed-red) to the spectrum for each LAE are presented in each panels. In each panel, luminosity, redshift and best-fit parameters such as w defining FWHM, and asymmetry parameter are given in the left corners.



































































