1 INTRODUCTION
Here, we briefly outline how the idea of dark matter (DM) emerged and when warm dark matter (WDM) branched off the mainstream theory. The idea that the temperature of DM impacts the distribution of structure in the universe is as old as the notion that galaxies cluster on large scales.
An important step in DM history, which started with the measurements of displacements within spiral galaxies to measure their rotation, was to realise that the dynamical properties of galaxies and galaxy clusters did not seem to match their observed luminous mass (see e.g. Zwicky Reference Zwicky1937; Schwarzschild Reference Schwarzschild1954; Janák Reference Janák1958; Abell Reference Abell1962; Burbidge & Sargent Reference Burbidge and Sargent1969; Paal Reference Paal1976, and references therein). Moreover, thanks to the first Palomar Observatory Sky Survey (1949-1958, Reid et al. Reference Reid1991), the distribution of galaxies in the sky was mapped for the first time in the mid 20th century and showed that galaxies conglomerated not only into clusters, but also gave rise to the cosmological ‘large-scale structure’ (Press & Schechter Reference Press and Schechter1974; Rudnicki Reference Rudnicki1976; White & Rees Reference White and Rees1978; Jones & Rees Reference Jones, Rees, Longair and Einasto1978; Wesson Reference Wesson1978; Aarseth & Fall Reference Aarseth and Fall1980), whose properties depended on cosmological parameters.
It thus became clear early on that the so-called ‘missing mass problem’ (e.g. Faber & Gallagher Reference Faber and Gallagher1979) was unlikely to be solved by dark gaseous matter, that it had to be dark stars, black holes, comets, or something else, like the conveniently weakly interacting massive particle—the neutrino. Assuming the missing mass was made up of massive neutrinos and other weakly interacting particles, an upper limit of 8 eV c−2 could be placed on their masses, assuming the measured expansion of the universeFootnote 1 (Cowsik & McClelland Reference Cowsik and McClelland1972).
The discovery of the cosmic microwave background (CMB) by Penzias & Wilson (Reference Penzias and Wilson1965); Dicke et al. (Reference Dicke, Peebles, Roll and Wilkinson1965) resulted in the acceptance of the Hot Big Bang origin of the universe. Big Bang Nucleosynthesis (BBN) put severe constraints on the amount of baryonic matter in the universe (Ωb ≪ 1, Schramm & Wagoner Reference Schramm and Wagoner1977; Olive, Steigman & Walker Reference Olive, Steigman and Walker2000, and references therein), and, combined with the requirement that the total density in the universe was close to the critical density for flatness,Footnote 2 gradually led to the belief that DM is made of new elementary particles.
One of the first candidates was a massive neutrino, but more general new particles were considered quickly, like other stable neutral leptons (Gunn et al. Reference Gunn, Lee, Lerche, Schramm and Steigman1978; Tremaine & Gunn Reference Tremaine and Gunn1979). The theory of supersymmety (SUSY) offered new candidate particles, like the gravitino with a keV mass (Pagels & Primack Reference Pagels and Primack1982), or the photino (Sciama Reference Sciama, Abell and Chincarini1983). In addition the axion, whose Jeans Mass would be smaller than galactic scales, was considered as a DM candidate (Stecker & Shafi Reference Stecker and Shafi1983; Shafi & Stecker Reference Shafi and Stecker1984). These particles were distributed in the universe as a perturbed density field, which became gravitationally coupled to the density field of baryons in the matter dominated era. However, because there was no energy dissipation for the particles of DM, they could not condense into bound objects easily. This was especially true for massive neutrinos with masses ~eV, whose damping scales reached the sizes of galaxy clusters and even superclusters (Bond, Efstathiou & Silk Reference Bond, Efstathiou and Silk1980; Schramm & Steigman Reference Schramm and Steigman1981). This meant that if the DM that was closing the universe was made up of massive neutrinos, the distributions of dark and luminous matter would have to be very different (Bruns & Zinnecker Reference Bruns and Zinnecker1983). In fact, in such a neutrino-dominated hot dark matter (HDM) model, the mechanism for galaxy formation was considered to be a fragmentation of large objects, which collapse first, as proposed by Zeldovich (Reference Zeldovich1970). These objects, which collapsed along one dimension first, were known as ‘pancakes’. After collapsing along two dimensions, they became filaments and finally spherically symmetric DM haloes.
The observations of the dynamics of galaxies, galaxy clusters, and superclusters were compared to the amount of visible mass by many authors (e.g. Bruns & Zinnecker Reference Bruns and Zinnecker1983, and references therein). A trend seemed to emerge, where the ‘missing mass’ fraction increased with object size, implying that the relation between the distributions of dark and luminous matter densities must be more biased on large scales.
Simultaneously, hierarchical merging of structure was considered via N-body simulations of the formation of the large-scale structure in the universe (Aarseth & Fall Reference Aarseth and Fall1980; White & Negroponte Reference White and Negroponte1982). In this picture, structure formed as a consequence of pure gravitational collapse of the initial linear density perturbations. Such ‘bottom-up’ hierarchical structure formation occurred if the matter density in the universe was dominated by particles more massive than at least several tens of eV (Bond, Szalay & Turner Reference Bond, Szalay and Turner1982), but it was not possible for the mν ~ 30 eV neutrinos (Peebles Reference Peebles1982). The bottom-up scenario became strongly favoured in 1984, since observations of dwarf galaxies as well as those of large-scale structure overall put strong lower limits on the mass of the DM particle (Lin & Faber Reference Lin and Faber1983; Kaiser Reference Kaiser1983; Madsen & Epstein Reference Madsen and Epstein1984). In other words, the standard model of DM became the cold dark matter (CDM) model.
However, Klypin et al. (Reference Klypin, Kravtsov, Valenzuela and Prada1999) noticed a discrepancy in the observed numbers of the smallest galaxies, assumed to reside within DM haloes with masses M dwarf ≤ 109 M ⊙ and what they expected these numbers to be from running their numerical simulations of structure formation with CDM. They proposed that the numerical simulations might be modified to account for this discrepancy, which has become known as the dwarf galaxy problem or missing satellite problem (Bode, Ostriker, & Turok Reference Bode, Ostriker and Turok2001), since the number of small objects observed fell significantly short of the expectation.
In recent years, N-body and hydro-dynamical codes have improved significantly in matching the small scales of ΛCDM to observations, for example via the suppression of the formation of baryonic objects within small DM haloes (e.g. ‘cosmic web stripping’, Benitez-Llambay et al. Reference Benitez-Llambay, Navarro, Abadi, Gottlöber, Yepes, Hoffman and Steinmetz2012). In addition, surveys like the Sloan Digital Sky Survey have found new dwarf galaxies around the Milky Way (see Bullock Reference Bullock2010, and references within for a review of the problem).
It is possible that this small-scale crisis of ΛCDM could be solved or alleviated with better numerical prescriptions for the complex baryonic processes (see e.g. Brooks et al. Reference Brooks, Kuhlen, Zolotov and Hooper2012) or it could be due to observational biases. However, the density profiles and concentrations of individual haloes (Donato et al. Reference Donato, Gentile, Salucci, Martins and Wilkinson2009) as well as the properties of voids (Tikhonov et al. Reference Tikhonov, Gottlöber, Yepes and Hoffman2009) do not seem to match what one would expect from pure ΛCDM model. Baryonic processes are difficult to invoke for explaining the properties of dwarf galaxies that are DM dominated, making it hard to fit their observational properties.
These long known ‘missing satellite’ and ‘core-cusp problems’ are related to more recently defined ‘too-big-to fail’ problem, being that the most massive Milky Way subhaloes from local ΛCDM simulations do not have dynamical properties similar to the observed Milky Way dwarf galaxies. For a recent review of the small-scale issues of ΛCDM see Weinberg et al. (Reference Weinberg, Bullock, Governato, Kuzio de Naray and Peter2013).
An elegant solution has been considered in the past, which has introduced WDM in a simple ΛWDM model with one additional parameter, which could explain all or some of these discrepancies. Because of its free-streaming, WDM is capable of damping the density field on small scales without any change to the large-scale behaviour of structure or to the dynamical evolution of space-time. For this reason we now discuss and summarise how to calculate non-linear corrections to predict the statistical properties of cosmological structure. This is not a straightforward task, but nonetheless, we describe attempts to develop a prescription valid also in ΛWDM models that may be used one day to account for some of the discrepancies at small scales of ΛCDM.
However, it should be noted that there exists a phase-space density imposed lower bound on the fermionic DM particle mass, called the Tremaine-Gunn bound (Tremaine & Gunn Reference Tremaine and Gunn1979; Hogan Reference Hogan1999), due to which it may not be possible for a WDM model to produce the relatively large cores that we seem to observe. Large halo cores can namely only be produced by very small particle mass, m wdm (Shao et al. Reference Shao, Gao, Theuns and Frenk2013). This has become known as the ‘too-small-to-succeed’ problem and put significant pressure on the WDM scenario.
In this review, we discuss the existing literature on constraining the WDM particle mass, m wdm, using the statistical properties of the large-scale structure. We choose this approach in hope that it may contain some information not contaminated by the uncertainties arising out of a lack of a rigorous model of baryonic feedback and cooling processes. There are many other works that look at individual objects of the large-scale structure and hope to constrain WDM from their properties (e.g. Pacucci, Mesinger, & Haiman Reference Pacucci, Mesinger and Haiman2013; Lovell et al. Reference Lovell, Eke, Frenk, Gao and Jenkins2012; Maccio et al. Reference Maccio, Paduroiu, Anderhalden, Schneider and Moore2012; Vinas, Salvador-Sole, & Manrique Reference Vinas, Salvador-Sole and Manrique2012; Sommer-Larsen & Dolgov Reference Sommer-Larsen and Dolgov2001).
In particular, we discuss in some detail the modelling of non-linear large-scale structure needed for comparison with data. We choose two observables to constrain our models: the Lyα forest and the cosmic shear (weak lensing) power spectrum, both of which require an accurate modelling of the non-linear matter power as a first step in the modelling of their basic properties. In Section 2, we summarise the general background physics of the smoothing of the linear matter density field by the free-streaming DM and the calculation of the linear matter power spectrum. We also briefly discuss the particle candidates for WDM. We then describe prescriptions for calculating the non-linear matter power spectra in the WDM scenario. In particular, we discuss N-body simulations, the halo model, and the current status of the two approaches for calculating the statistics of the large scales in the universe. We summarise the current limits coming from the Lyα forest data in Section 3, which present the strongest constraints on the temperature of DM to date. Finally, we report on forecasts that have been made on the WDM temperature obtained from future weak lensing surveys like EuclidFootnote 3 in Section 3.2.
2 GENERAL FRAMEWORK
Neutrinos decouple when the temperature of the primordial plasma is T ~ 1 MeV and a ~ 10−10 and become non-relativistic when T h ~ m h/3k B.Footnote 4 DM decouples and becomes non-relativistic much earlier in both the CDM and WDM cases. If WDM has a simple thermal history, analogous to neutrinos, but with a larger particle mass, we can calculate its free-streaming. Such a DM particle is called a thermal relic, because it was once in equilibrium with itself.
The Jeans length can be calculated for a perfect fluid and denotes the limit on which the gravitational effect balance out the thermal effects (Bond & Szalay Reference Bond and Szalay1983). For collisionless fluids like the DM and neutrino fluids, we can define the analogous comoving free-streaming wavenumber, which tells how far the fast-moving particles can travel within the gravitational time-scale, i.e. in the time of free-fall (Boyarsky et al. Reference Boyarsky, Lesgourgues, Ruchayskiy and Viel2009a):
In fact, even in mixed DM models (C+HDM), where the HDM component makes up a small fraction of the total energy density as in the ΛCDM + neutrinos, νΛCDM, the perturbations in the cold component are modified by the free-streaming of the HDM. In this scenario the larger scales suffer more free-streaming damping and therefore the perturbations in the HDM cannot grow until late times, which gravitationally affects the perturbations in the cold component, slowing down the growth of the perturbation amplitudes (Primack & Gross Reference Primack and Gross1998; Ghigna et al. Reference Ghigna, Borgani, Tucci, Bonometto, Klypin and Primack1997; Klypin et al. Reference Klypin, Borgani, Holtzman and Primack1995; Nolthenius, Klypin & Primack Reference Nolthenius, Klypin and Primack1994; Klypin et al. Reference Klypin, Holtzman, Primack and Regos1993; Gawiser & Silk Reference Gawiser and Silk1998; Primack Reference Primack1997; Primack et al. Reference Primack, Holtzman, Klypin and Caldwell1995; Ma & Bertschinger Reference Ma and Bertschinger1995; Zentner & Bullock Reference Zentner and Bullock2003; Primack Reference Primack2003).
The most basic model of WDM particles is to assume that they are thermal relics. This means that they were in thermal equilibrium at some point. When their temperature and density dropped, they went out of equilibrium (e.g. Bond & Szalay Reference Bond and Szalay1983) and DM particles decoupled from each other. Instead, the sterile neutrino particles, that will be discussed later, were never in thermal equilibrium.
Theoretically there would have been another kind of decoupling. This would have been when DM particles and baryons were in an extremely dense environment and so there would have been a significant interaction rate between them. We know very little about this regime, because we would have to know the mass and interaction cross-section of DM particles, but we do not even know the nature of the interaction (if any) between DM particles and other types of matter.
However, it is most likely that these two decouplings happened at the same time, because any self-interaction of DM is likely to involve the weak, strong, or electromagnetic force, which means this self-interaction would necessarily involve baryons. Were this not the case, it may be that the interaction between baryons and DM particles is weaker than the interaction among DM particles. In this case the decoupling from baryons would happen at an earlier time than decoupling of DM out of equilibrium.
The smallest important scale feature in the linear matter power spectrum is the suppression induced by DM free-streaming. In the WDM model the scale of suppression is called the free-streaming scale, k fs, and corresponds to the mode that enters the horizon at the time when WDM particles become non-relativistic, t rel. A species can become non-relativistic while still in thermal equilibrium or after it decouples (Bond & Szalay Reference Bond and Szalay1983; Bode et al. Reference Bode, Ostriker and Turok2001; White et al. Reference White, Frenk, Davis and Efstathiou1987). If it is after, we say that DM particles decouple while non-relativistic. This is what we often assume in modelling the large-scale structure in these models, for the sake of simplicity.
From Bond & Szalay (Reference Bond and Szalay1983), we get the temperature of WDM relative to that of the photons, from which one can calculate the total WDM density for a particular particle model (giving g wdm and m wdm):
 \begin{equation}
\Omega _{\rm wdm}= \frac{1.1}{h^{2}}\left(\frac{100}{3.9}\right)\left(\frac{g_{\rm wdm}}{1.5}\right) \left(\frac{T_{\rm wdm}}{T_\gamma }\right)^3\left(\frac{m_{\rm wdm}}{1 \,{\rm keV}}\right),
\end{equation}
\begin{equation}
\Omega _{\rm wdm}= \frac{1.1}{h^{2}}\left(\frac{100}{3.9}\right)\left(\frac{g_{\rm wdm}}{1.5}\right) \left(\frac{T_{\rm wdm}}{T_\gamma }\right)^3\left(\frac{m_{\rm wdm}}{1 \,{\rm keV}}\right),
\end{equation}
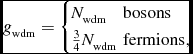 \begin{equation}
g_{\rm wdm}= \left\lbrace\! \begin{array}{ll}N_{\rm wdm}& {\rm bosons} \\[3pt]
\frac{3}{4}N_{\rm wdm}& {\rm fermions}, \end{array} \right.
\end{equation}
\begin{equation}
g_{\rm wdm}= \left\lbrace\! \begin{array}{ll}N_{\rm wdm}& {\rm bosons} \\[3pt]
\frac{3}{4}N_{\rm wdm}& {\rm fermions}, \end{array} \right.
\end{equation}
In addition we can calculate the velocity dispersion of WDM particles relative to that of the neutrinos (Bond et al. Reference Bond, Efstathiou and Silk1980):
Rescaling for WDM, if it has decoupled while relativistic:
If particles decouple while non-relativistic,
![]() $\sqrt{\langle v^2\rangle_{\rm wdm}} \lesssim \, {\rm cm\, s}^{-1}$
, so any further damping is insignificant and the species becomes effectively ‘cold’.
$\sqrt{\langle v^2\rangle_{\rm wdm}} \lesssim \, {\rm cm\, s}^{-1}$
, so any further damping is insignificant and the species becomes effectively ‘cold’.
2.1 The linear power spectrum
In the case of WDM, the initial matter power spectrum emerging from radiation domination is modified by an additional transfer function due to free streaming. Viel et al. (Reference Viel, Lesgourgues, Haehnelt, Matarrese and Riotto2005) used a fitting function that can however be calculated very accurately with a numerical Boltzmann equation solver code, like for example CMBFAST (Seljak & Zaldarriaga Reference Seljak and Zaldarriaga1996), CAMB (Lewis, Challinor & Lasenby Reference Lewis, Challinor and Lasenby2000), or CLASS (Blas, Lesgourgues, & Tram Reference Blas, Lesgourgues and Tram2011; Lesgourgues Reference Lesgourgues2011; Lesgourgues & Tram Reference Lesgourgues and Tram2011). These codes solve the equations describing the growth of perturbations in the radiation dominated universe in a semi-analytic line-of-sight approach.
The fitting function of Viel et al. (Reference Viel, Lesgourgues, Haehnelt, Matarrese and Riotto2005) with ν = 1.12 (the alternative is ν = 1.2 like in Bode et al. Reference Bode, Ostriker and Turok2001) contains a scale-break parameter, which is used in calculating the linear matter power spectrum by multiplying with the following WDM transfer function:
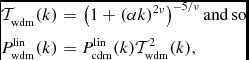 \begin{eqnarray}
\mathcal {T}_{\rm wdm}(k) &=& \left(1+(\alpha k)^{2\nu }\right)^{-5/\nu } {\rm and\, so} \\
P^{\rm lin}_{\rm wdm}(k) &=& P^{\rm lin}_{\rm cdm}(k) \mathcal {T}^2_{\rm wdm}(k),\nonumber
\end{eqnarray}
\begin{eqnarray}
\mathcal {T}_{\rm wdm}(k) &=& \left(1+(\alpha k)^{2\nu }\right)^{-5/\nu } {\rm and\, so} \\
P^{\rm lin}_{\rm wdm}(k) &=& P^{\rm lin}_{\rm cdm}(k) \mathcal {T}^2_{\rm wdm}(k),\nonumber
\end{eqnarray}
Alternatively, Boyanovsky, de Vega & Sanchez (Reference Boyanovsky, de Vega and Sanchez2008b) found a transfer function for a general initial thermal distribution of DM particles—cold WIMP DM, thermal fermionic, or bosonic DM.
The linear power spectrum, P lin wdm(k), must then be normalised to ensure the value σ2 8 at R = 8h − 1Mpc. Finally we now can plot the linear matter power spectra in Figure 1. The lightest WDM particle mass shown (500 eV) causes the linear theory matter power spectrum to be suppressed dramatically at a wavenumber significantly above 1 hMpc− 1 . The matter power spectrum of WDM starts to turn off well above the free-streaming scale, which changes the slope of the power spectrum to fall much more steeply than n eff = log P(k)/log k = −3, which is the slope for standard, bottom-up structure formation (White & Frenk Reference White and Frenk1991; Knebe et al. Reference Knebe, Devriendt, Gibson and Silk2003).

Figure 1. Left: The linear matter power spectra for three different WDM models and standard CDM. The particle masses, m wdm ∈ {0.5, 1.0, 2.0}keV, are colour coded with magenta, red, and cyan, respectively. The vertical lines correspond to a tenth of the free-streaming wavenumber, k fs/10, for each model of WDM. These power spectra were produced using the Boltzmann solver CLASS (Lesgourgues Reference Lesgourgues2011).
Right: ratios between the WDM and CDM power spectra, P wdm(k)/P cdm(k), to clearly see the suppression with respect to the k fs/10.
In fact the above seemingly artificial scale break, α, relates to the free-streaming length of thermal relic WDM particles (Zentner & Bullock Reference Zentner and Bullock2003):
We plot k fs/10 in Figure 1, because it is the scale around which the significant suppression of the power in the linear matter power spectrum begins. It is an interesting open-ended question why the free-streaming suppression reaches scales so much larger than the free-streaming scale. This has been explored, among others, by Smith & Markovič (Reference Smith and Markovič2011).
In addition, we can define a corresponding mass found, on average, in a volume with such a radius or free-streaming mass:
In Figure 2, we plot the linear matter power spectrum alongside the CMB power spectrum for the HDM scenario to illustrate the impact on the CMB and matter power of such a small mass candidate; it is thus clear that heavier masses will impact much less on these two observables at the largest scales. We plot the power spectra in the neutrino-like (but with m ~ 10eV) scenario being all of DM. We expect the power spectra to be suppressed at very large l due to the free-streaming effect and to increase for small l, due to a mixture of two effects: changes in the matter-radiation equality and because the primordial power spectrum is normalised at k = 0.05hMpc− 1 causing the small-scale-suppressed power spectrum to be boosted on large scales.

Figure 2. We plot the effect of a hot thermal relic particle (hotter than a WDM candidate) on the cosmic microwave background C(l)’s: we show models that have been long ruled out, where all the DM is made up of very light, neutrino-like particles with masses of m wdm = 0.005 and 0.01keV.
Left: The three-dimensional linear matter power spectrum, P(k), for CDM (black) and the two ‘HDM’ models (magenta and red, respectively). Compare this extreme case to the more plausible models in Figure 1 that will impact at a much smaller level. Right: The CMB un-lensed C(l)’s in the corresponding HDM models. The cosmological model is the Planck best fit as in the rest of the paper, the error bars are those of Planck survey (Planck Collaboration et al. 2013).
Since, l = 2000 corresponds to about a k ~ 0.2 hMpc−1 at z CMB = 1000, we expect the effect on the CMB from reasonable WDM scenarios to be completely negligible. In the right panel of Figure 1 it can be noted that at k = 0.2, hMpc−1, the suppression is clearly less than 1% for m wdm = 1keV.
2.2 Sterile neutrinos
We have discussed some of the particle candidates for DM in this introductory section of this review. A further hypothetical particle that has sparked interest is the sterile neutrino, which does not require an extension of the Standard Model with SUSY (Dodelson & Widrow Reference Dodelson and Widrow1994; Fuller et al. Reference Fuller, Kusenko, Mocioiu and Pascoli2003; Asaka, Blanchet & Shaposhnikov Reference Asaka, Blanchet and Shaposhnikov2005; Abazajian Reference Abazajian2006; Boyarsky et al. Reference Boyarsky, Neronov, Ruchayskiy and Shaposhnikov2006; Petraki & Kusenko Reference Petraki and Kusenko2008; Laine & Shaposhnikov Reference Laine and Shaposhnikov2008; Kusenko Reference Kusenko2009; Hamann et al. Reference Hamann, Hannestad, Raffelt, Tamborra and Wong2010; Boyarsky, Iakubovskyi & Ruchayskiy Reference Boyarsky, Iakubovskyi and Ruchayskiy2012). Sterile neutrinos are assumed to be singlet right-handed particles that become relatively heavy compared to standard, active neutrinos, which receive small masses via a see-saw mechanism (Dodelson & Widrow Reference Dodelson and Widrow1994). The lightest of the additional neutrinos can then have a mass in the keVrange, meaning that it resembles a WDM. However, the sterile neutrinos are assumed to never have been in thermal equilibrium; therefore, their abundance was suppressed.
In the above calculation of the free-streaming scale we have used three parameters that describe the thermal relic WDM model: the particle mass, m wdm, the energy density, Ωwdm, and the temperature T wdm, where the degrees of freedom at WDM decoupling, g*wdm, are determined solely by the particle mass and its energy density. We can conveniently re-parametrise the particle mass of the never-thermalised sterile neutrino in terms of the thermal relic mass, such that they are interchangeable in the calculation of the impact of their free-streaming on the large-scale structure:
2.3 The non-linear power spectrum
Now that we have shown the effects of WDM on the linear matter density field we must outline some tools for the standard model of structure formation. In the matter dominated era, the density contrast grows and eventually reaches unity, where non-linearities must be properly accounted for and modelled. From this point on, standard perturbation theory is no longer appropriate and we must employ approximation methods as exact solutions to the Einstein field equations no longer exist.
It is necessary to have a robust model of non-linear structure in order to take full advantage of future weak lensing data. For this reason we compare the non-linear matter power spectra extracted from simulations with derived non-linear models. The halo model of non-linear structure is based on the assumption that large-scale structure is made up of individual objects occupying peaks in the matter over-density field (Press & Schechter Reference Press and Schechter1974; Seljak Reference Seljak2000; Cooray & Sheth Reference Cooray and Sheth2002). The most important elements of this model, the mass function, the halo bias (Press & Schechter Reference Press and Schechter1974), and the halo density profile (Navarro, Frenk, & White Reference Navarro, Frenk and White1997), are based on the assumptions that all DM in the universe is found in haloes and that there is no observable suppression of small-scale over-densities from early-times free-streaming of DM particles or late-times thermal velocities.
These are characteristic properties of CDM, but do not apply to WDM. For this reason one should re-visit the modelling of cosmological structure. Smith & Markovič (Reference Smith and Markovič2011); Schneider et al. (Reference Schneider, Smith, Maccio and Moore2012); Dunstan et al. (Reference Dunstan, Abazajian, Polisensky and Ricotti2011); Schneider, Smith, & Reed (Reference Schneider, Smith and Reed2013b); and Angulo, Hahn, & Abel (Reference Angulo, Hahn and Abel2013) modified the halo model by applying a specific prescription to the non-linear contribution, in addition to suppressing the initial density field, modelled by applying a transfer function from Equation (7) to the linear matter power spectrum. We discuss the halo model in Section 2.3.2. However, we wish to first summarise some results from N-body simulations.
2.3.1 WDM simulations
N-body simulations have long been considered important in calculating the properties of the large-scale structure of DM and the formation of this structure in the CDM scenario (Appel Reference Appel1985; Barnes & Hut Reference Barnes and Hut1986; Katz, Weinberg & Hernquist Reference Katz, Weinberg and Hernquist1996; Frigo Reference Frigo1999; Bagla & Ray Reference Bagla and Ray2003; Springel Reference Springel2005). In recent years, this method has also been applied to the WDM case (Boehm et al. Reference Boehm, Mathis, Devriendt and Silk2005; Boyanovsky, de Vega & Sanchez Reference Boyanovsky, de Vega and Sanchez2008a; Wang & White Reference Wang and White2007; Zavala et al. Reference Zavala, Jing, Faltenbacher, Yepes, Hoffman, Gottlöber and Catinella2009; Colombi et al. Reference Colombi, Jaffe, Novikov and Pichon2008; Viel et al. Reference Viel, Markovič, Baldi and Weller2012; Schneider et al. Reference Schneider, Smith, Maccio and Moore2012; Dunstan et al. Reference Dunstan, Abazajian, Polisensky and Ricotti2011; Benson et al. Reference Benson, Farahi, Cole, Moustakas, Jenkins, Lovell, Kennedy, Helly and Frenk2012; Semenov et al. Reference Semenov, Pilipenko, Doroshkevich, Lukash and Mikheeva2013). Numerical convergence for WDM (and HDM) simulations is particularly difficult to achieve as pointed out by Wang & White (Reference Wang and White2007). The reason is due to the spurious fragmentation of filaments that give rise to a pattern of small mass haloes. This effect can be alleviated by increasing the number of particles (although convergence is slow) or by preventing the fragmentation of such structures. In any case, convergence tests of the relevant simulated physical quantities (like the Lyα forest flux and/or the mass function or matter power spectrum) must be performed in order not to be affected by this at the scales or redshifts of interest. A post hoc solution was proposed by Schneider et al. (Reference Schneider, Smith and Reed2013b), which does not solve the problem, but corrects the result via subtraction of spurious haloes, while Lovell et al. (Reference Lovell, Frenk, Eke, Jenkins, Gao and Theuns2013) identifies spurious haloes in the initial conditions.
N-body simulations assume that collapsing matter is non-relativistic (ρ ≫ P) and that collapse is only possible on sub-horizon scales (k ≫ aH). Therefore in ΛCDM, the non-relativistic, Newtonian perturbation equations are sufficient and so, the collisionless Boltzmann and Poisson equation are solved in a discreet way.
These equations are normally solved by an N-body code, e.g. Gadget (Springel, Yoshida & White Reference Springel, Yoshida and White2001). It is difficult to achieve this simply with finite difference methods, so Monte-Carlo-like N-body simulations are employed to integrate the Boltzmann equations of N particles populating the phase space, using the method of characteristics.Footnote 6
Smith et al. (Reference Smith2003) compared the standard CDM halo model to CDM simulations of large-scale structure formation and developed an analytical fit to the non-linear corrections of the matter power spectrum, known as halofit. Markovič et al. (Reference Markovič, Bridle, Slosar and Weller2011) and Viel et al. (Reference Viel, Markovič, Baldi and Weller2012) applied these corrections to a linear matter power suppressed by the Viel et al. (Reference Viel, Lesgourgues, Haehnelt, Matarrese and Riotto2005) WDM transfer function (Equation 7). Viel et al. (Reference Viel, Markovič, Baldi and Weller2012) ran cosmological N-body simulations (DM only) in the WDM scenario (see Figure 3). They found that the WDM halo model is closest to simulations at z = 1 for 1keV WDM, but that it over-estimates the suppression effect at z = 0.5 for 0.5keV WDM by about 5% on scales k > 1hMpc− 1. On scales k < 1hMpc− 1 however, the halofit non-linear correction describes the simulations better than the halo model, even though on smaller scales it severely underestimates the suppression effect, which becomes worse at lower redshifts. A further small modification of the WDM halo model improves its correspondence to the simulations and allows one to use it at small scales (Section 2.3.2).

Figure 3. We plot the projected DM overdensity from a high-resolution hydro-dynamical simulation of Viel et al. (Reference Viel, Markovič, Baldi and Weller2012), at redshifts z = 0 (upper panels) and z = 2 (lower panels) for ΛCDM and 1keV WDM, in the left and right columns, respectively. The amount of substructure present in the ΛCDM model is more pronounced with respect to the WDM one. The box size is 25 comoving Mpc h−1 and the thickness is 5 comoving Mpc h−1.
Viel et al. (Reference Viel, Markovič, Baldi and Weller2012) consider varying resolutions and WDM models. These simulations were run using the N-body code Gadget-2, for which the initial conditions were generated using the WDM-suppressed linear matter power spectrum in Equation (7). In Figure 4 we see plotted the percentage differences between the WDM and CDM non-linear matter power spectra for several different WDM models, denoted by the different thermal relic particle masses. This plot shows the suppression effect growing not only with decreasing particle mass (i.e. increasing WDM temperature), but also with increasing redshift and demonstrates the effect that the WDM signal is erased with time due to the non-linear growth of structure. It may be noted that the free-streaming scale below which the power spectrum becomes exponentially suppressed is of the order of k ~ 1hMpc− 1 for 1keV WDM particles. The authors found a fitting function that can be used to calculate the non-linear matter power spectrum in the WDM scenario from the CDM P nl(k) analogously to Equation (7):

Figure 4. Percentage differences between WDM and CDM non-linear matter power spectra from hydro-dynamical simulations at high-resolution. The solid lines show the large-scale power, while the dashed lines describe the small-scale power obtained with the folding method in order to reach smaller scales (see Jenkins et al. Reference Jenkins1998; Colombi et al. Reference Colombi, Jaffe, Novikov and Pichon2008, for details). The dotted line is the suppression to the linear matter power spectrum and is the same both in the z = 3 and z = 0 panels. The different panels show z = 0, 0.5, 1.2, 3. Note that the steep rise on scales, k > 50 hMpc− 1, is affected by the poor resolution of the WDM simulations and it is not fully physical (although an increase of power could be expected and it might be due to the different DM density profile at small scales).
Assuming WDM to be thermal relic fermions, their relic velocities have a Fermi-Dirac distribution, which can be added to the proper velocities calculated from the gravitational potentials from linear theory. The velocities for some of the WDM models they use can be found to be: v th ∈ {27.9, 11.5, 4.4, 1.7, 0.7}kms− 1 for m wdm ∈ {0.25, 0.5, 1, 2, 4}keV, respectively. For comparison, the typical root mean square (r.m.s.) value for the velocity in a ΛCDM run is v g ~ 30kms− 1, so it is significantly larger than any thermal velocities of WDM particles in the models that are still allowed by for example the Lyα forest (m wdm ≳ 2keV).
It has been shown by many authors (e.g. Schaye et al. Reference Schaye2010; van Daalen et al. Reference van Daalen, Schaye, Booth and Vecchia2011; Casarini et al. Reference Casarini, La Vacca, Amendola, Bonometto and Maccio2011; Semboloni et al. Reference Semboloni, Hoekstra, Schaye, van Daalen and McCarthy2011) that baryons, making up 17% of the total matter density, affect the distribution of DM on small scales significantly. Simple hydro-dynamical simulations in WDM and ΛCDM were run by Viel et al. (Reference Viel, Markovič, Baldi and Weller2012). They include a prescription for radiative cooling and heating, where all the cooling comes from Hydrogen and Helium (Katz et al. Reference Katz, Weinberg and Hernquist1996, as in) and no metal cooling is considered. The prescription for modelling the cooling and the star formation criterion are described in more detail in Viel, Haehnelt, & Springel (Reference Viel, Haehnelt and Springel2004) and is called ‘quick Lyα’, since it can be used in order to speed up the hydro-dynamics with practically no impact on the Lyα forest flux statistics (this simulation is labelled as ‘BARYONS+QLYA’). A further simulation has also been run that uses a more refined star formation criterion and strong galactic winds powered by the thermal feedback of supernovae (this simulation is labelled as ‘BARYONS+SF+WINDS’).
We plot in Figure 5 the resulting percentage difference between a 1keV WDM and CDM non-linear matter power spectrum, where both come from simulations that include cooling and heating processes from the ultraviolet background and a simple star formation criterion. Out of these simulations, one included galactic winds had to be stopped at z = 1.2 due to limited computational resources and is therefore plotted above this redshift. It can be seen in Figure 5 that the inclusion of baryonic processes can have a very significant scale and redshift-dependent effect on the suppression signal of WDM. It seems likely that some baryonic processes become more efficient in a collapsing over-density field that has been smoothed. Because the baryonic processes affect the power on small scales, this can erase the suppression from WDM, which is relevant on similar scales (see also Gao & Theuns Reference Gao and Theuns2007).

Figure 5. WDM suppression for three different simulations with and without baryons. These three different simulations are compared with the corresponding ΛCDM run with the same initial conditions. DMONLY is the resulting percentage difference between the WDM and CDM non-linear matter power spectrum (green), BARYONS+QLYA includes cooling due to H and He (blue), and BARYONS+SF+WINDS, which includes star formation and strong galactic winds (black). The prescription used for the star formation processes is labelled as ‘quick Lyα’ from Viel et al. (Reference Viel, Haehnelt and Springel2004). We show two different redshifts: z = 1.4 and z = 0.
It has also recently been reported by the authors of the OWLS simulations (van Daalen et al. Reference van Daalen, Schaye, Booth and Vecchia2011; Semboloni et al. Reference Semboloni, Hoekstra, Schaye, van Daalen and McCarthy2011, etc.) that the effects of baryonic processes, in particular the feedback from active galactic nuclei (AGN), can become dominant on scales that are significant to cosmology. This is certainly an important issue to consider in the future in order to realistically model the non-linear matter power.
2.3.2 The WDM halo model
It is interesting to note that even in the standard CDM scenario with WIMPy DM particles there exists a minimum free-streaming halo mass, which is very low. Green, Hofmann & Schwarz (Reference Green, Hofmann and Schwarz2005); Hofmann, Schwarz & Stöcker (Reference Hofmann, Schwarz and Stöcker2001); Schneider et al. (Reference Schneider, Smith and Reed2013b) find such CDM minimum haloes have masses of M ~ 10−6 M ⊙. In WDM models, this minimum mass is significantly larger. We explore this and other side effects of the primordial free-streaming of WDM on the properties and distribution of DM haloes in this section with reference to mostly the work of Markovič et al. (Reference Markovič, Bridle, Slosar and Weller2011); Smith & Markovič (Reference Smith and Markovič2011); Schneider et al. (Reference Schneider, Smith, Maccio and Moore2012) and less so that of Cooray, Hu & Miralda-Escude (Reference Cooray, Hu and Miralda-Escude2000); Cooray & Sheth (Reference Cooray and Sheth2002); Abazajian et al. (Reference Abazajian, Switzer, Dodelson, Heitmann and Habib2005); Zavala et al. (Reference Zavala, Jing, Faltenbacher, Yepes, Hoffman, Gottlöber and Catinella2009); Dunstan et al. (Reference Dunstan, Abazajian, Polisensky and Ricotti2011); Lovell et al. (Reference Lovell, Eke, Frenk, Gao and Jenkins2012); Pacucci et al. (Reference Pacucci, Mesinger and Haiman2013). We do not discuss the work of Angulo et al. (Reference Angulo, Hahn and Abel2013); Schneider et al. (Reference Schneider, Smith and Reed2013b) here in detail, but it is worth noting that they also modified the halo mass function such that it works well in fitting the results of numerical methods.
The halo model of large-scale structure offers a tool to quantify the non-linear structure growth. It is based on the spherical collapse model, where the over-densities of the matter density field collapse as spherically symmetric objects. In the most rudimentary form, the halo model assumes that all matter can be found within DM haloes, which merge into larger and larger haloes with time (i.e. ‘bottom-up’), stopping only around the present time, when further non-linear collapse is halted by the emergence of the ‘dark energy’ componentFootnote 7 .
The halo model assumes that halo positions are sampled from the linear theory matter distribution. As a result, there are two main contributions to the non-linear matter power spectrum. Firstly, the two-halo term, P
C(k), which dominates on large scales, encodes the correlation between different haloes and is equal to the linear matter power spectrum on large scales, P
lin. Secondly, the one-halo term, P
P(k), refers to the correlations within a halo and therefore depends mostly on the Fourier transform of the density profile of the halo,
![]() $\tilde{\rho }(k,M,z)$
. Both terms depend on the number of haloes as a function of halo mass, dn/dM, which can be found to a reasonable approximation using analytic arguments or more usually measured from numerical simulations. The total non-linear matter power spectrum from the halo model is a sum of the two terms:
$\tilde{\rho }(k,M,z)$
. Both terms depend on the number of haloes as a function of halo mass, dn/dM, which can be found to a reasonable approximation using analytic arguments or more usually measured from numerical simulations. The total non-linear matter power spectrum from the halo model is a sum of the two terms:
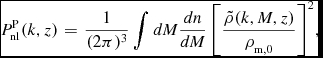 \begin{eqnarray}
P^{{\rm P}}_{{\rm nl}}(k,z)&=&\frac{1}{(2\pi )^3}\int dM\frac{dn}{dM}\left[\frac{\tilde{\rho }(k,M,z)}{\rho _{{\rm m},0}}\right]^2\!,
\end{eqnarray}
\begin{eqnarray}
P^{{\rm P}}_{{\rm nl}}(k,z)&=&\frac{1}{(2\pi )^3}\int dM\frac{dn}{dM}\left[\frac{\tilde{\rho }(k,M,z)}{\rho _{{\rm m},0}}\right]^2\!,
\end{eqnarray}
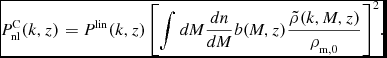 \begin{eqnarray}
P^{{\rm C}}_{{\rm nl}}(k,z)&=&P^{{\rm lin}}(k,z)\left[\int dM\frac{dn}{dM}b(M,z)\frac{\tilde{\rho }(k,M,z)}{\rho _{{\rm m},0}} \right]^2\!.\quad
\end{eqnarray}
\begin{eqnarray}
P^{{\rm C}}_{{\rm nl}}(k,z)&=&P^{{\rm lin}}(k,z)\left[\int dM\frac{dn}{dM}b(M,z)\frac{\tilde{\rho }(k,M,z)}{\rho _{{\rm m},0}} \right]^2\!.\quad
\end{eqnarray}
Attempts have been made by Smith & Markovič (Reference Smith and Markovič2011); Schneider et al. (Reference Schneider, Smith, Maccio and Moore2012); Dunstan et al. (Reference Dunstan, Abazajian, Polisensky and Ricotti2011) to extend the halo model to WDM scenarios by modifying its ingredients. They use the WDM linear power spectrum to calculate a new mass function using the Sheth & Tormen (Reference Sheth and Tormen1999) prescription. They make the conservative assumption that the halo profiles are unchanged relative to CDM. It is in the one-halo term of the power spectrum that the effects of free-streaming of WDM are seen most strongly. This is because of the difference in the r.m.s. fluctuation, σ(R), which becomes suppressed at small R in a WDM universe. This effect is shown in Figure 6 for two rather extreme WDM models, with very low particle masses. We plot this to show that for very low-mass DM particles (this is effectively HDM), the over-density field variance never reaches the necessary value for spherical collapse. This results in an extreme suppression of the formation of structure, ruling out the domination of the DM density by HDM.

Figure 6. The root-mean-square density fluctuation for CDM (top, solid line), 0.1keV WDM (bottom), and 0.25keV (middle). The σ(M) flattens off for the smallest halo masses in the WDM model, as one would expect for any smoothed field. The dotted black line indicates the critical over-density for spherical collapse.
We explore the effect of WDM on the mass functions in Figure 7. As expected, the number density for the smallest haloes is reduced in the case of WDM. This is shown most visibly in the left panel of Figure 7. This is useful for comparison to the general assumption of the absence of haloes below the free-streaming halo mass, defined in Equation (11) (Avila-Reese et al. Reference Avila-Reese, Colin, Valenzuela, D'Onghia and Firmani2001). The definition of the free-streaming mass is somewhat arbitrary, because it does not really correspond to a physical halo, since it does not include the density contrast parameter, Δ (as it does in Sommer-Larsen & Dolgov Reference Sommer-Larsen and Dolgov2001). For this reason Schneider et al. (Reference Schneider, Smith, Maccio and Moore2012) proposed to define instead the half-mode halo mass, which denotes the halo mass at which the mass functions become suppressed by a factor of 1/2:
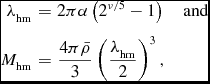 \begin{eqnarray}
\lambda _{\rm hm} &=& 2\pi \alpha \left(2^{\nu /5} - 1\right)\quad {\rm and}\nonumber \\
M_{\rm hm} &=& \frac{4\pi \bar{\rho }}{3}\left(\frac{\lambda _{\rm hm}}{2}\right)^3,
\end{eqnarray}
\begin{eqnarray}
\lambda _{\rm hm} &=& 2\pi \alpha \left(2^{\nu /5} - 1\right)\quad {\rm and}\nonumber \\
M_{\rm hm} &=& \frac{4\pi \bar{\rho }}{3}\left(\frac{\lambda _{\rm hm}}{2}\right)^3,
\end{eqnarray}

Figure 7. On the left we plot the mass functions from Sheth & Tormen (Reference Sheth and Tormen1999) (dotted) vs. Schneider et al. (Reference Schneider, Smith, Maccio and Moore2012) fit to simulations (solid). On the right we show the re-scaled ratios of these mass functions by the half-mode halo mass, M hm. The half-mode and the free-streaming halo masses are plotted with crosses and asterisks, respectively.
Schneider et al. (Reference Schneider, Smith, Maccio and Moore2012) examined the halo model in comparison to N-body simulations. They re-scaled the halo masses with respect to the half-mode mass, M hm ≈ 2.7 × 103 M fs, rather than the free-streaming mass as above. They find the simple fitting formula:

Figure 8. This figure compares the halo mass that corresponds to the ratio between WDM and CDM mass functions falling to a half, called the half-mode mass, M hm, and the free-streaming halo mass for WDM particles with masses m wdm, M fs.
This modification was motivated by the simulated mass function declining much more steeply than the Sheth & Tormen (Reference Sheth and Tormen1999) already seen by Zavala et al. (Reference Zavala, Jing, Faltenbacher, Yepes, Hoffman, Gottlöber and Catinella2009). This suggests that Sheth & Tormen (Reference Sheth and Tormen1999) prescription underestimates the effect of WDM on the mass functions. On the other hand, there could be unforeseen resolution effects coming from the simulations. However, this is unlikely since there are usually spurious haloes created in WDM simulations, which for the Zavala et al. (Reference Zavala, Jing, Faltenbacher, Yepes, Hoffman, Gottlöber and Catinella2009) simulations increases the mass function M ≲ 109 M ⊙.
Interestingly, Schneider et al. (Reference Schneider, Smith, Maccio and Moore2012) also suggest a re-scaling of the concentration parameter to suit the simulation results better. We also plot the NFW (Navarro et al. Reference Navarro, Frenk and White1997) halo density profiles calculated using the new WDM concentration parameter (Seljak Reference Seljak2000) re-scaling in Figure 9.

Figure 9. NFW (Navarro et al. Reference Navarro, Frenk and White1997) halo density profiles for two different halo masses (1010 and 1012 M ⊙) calculated with the re-scaled concentration parameter from Schneider et al. (Reference Schneider, Smith, Maccio and Moore2012) for WDM models with m wdm ∈ {0.25, 0.5, 1.0, 2.0, 10.0}keV. The dashed vertical lines correspond to the free-streaming lengths in the different WDM models, re-scaled by the virial radius of the halo.
Unfortunately, the modifications to the halo model do not seem to adequately describe the evolution of the WDM suppression with redshift. For this reason it is still the Viel et al. (Reference Viel, Markovič, Baldi and Weller2012) fitting function for the P nl wdm(k) that best fits the results from the above-mentioned simulations. We plot the ratios of the WDM vs. CDM non-linear matter power spectra in Figure 10.

Figure 10. Ratios of non-linear matter power spectra in the different models, P nl wdm(k)/P nl cdm(k) for 500eV and 1keV WDM particles at z = 0 on top and z = 0.5 at the bottom. The dotted red lines show the P C(k) and P P(k) dominating at small and large k, respectively. The red solid lines show the halo model modified like in Schneider et al. (Reference Schneider, Smith, Maccio and Moore2012). The cyan dash-dotted line shows the older modification of the halo model by Smith & Markovič (Reference Smith and Markovič2011). The green dash-dotted line is the simplest version of the halo model with standard Sheth & Tormen (Reference Sheth and Tormen1999) mass functions.
Very recently however, Benson et al. (Reference Benson, Farahi, Cole, Moustakas, Jenkins, Lovell, Kennedy, Helly and Frenk2012); Schneider et al. (Reference Schneider, Smith and Reed2013b) proposed that the mass functions should be calculated with the standard Sheth & Tormen (Reference Sheth and Tormen1999) prescription, but using a sharp-k filter to find the σ(R) instead of the real-space top-hat. This seems to describe the redshift evolution of the WDM suppression better. On the other hand, Pacucci et al. (Reference Pacucci, Mesinger and Haiman2013) propose to raise the collapse threshold to emulate the difficulty of collapse in the WDM scenario and calculate the mass functions at high redshift.
3 PRESENT AND FUTURE CONSTRAINTS
Using the methods described above, one can model the structure in the universe and compare the resulting power spectra to observations. In this section we will review the constraints that are obtained and could be obtained from the two most powerful small-scale observables: the Lyα forest and weak lensing.
3.1 The Lyman-α forest
The Lyα forest, the absorption induced by intervening neutral hydrogen along the line-of-sight to a distant quasar, is a powerful cosmological tool ideally suited to probe the clustering of matter over a range of scales from below the Mpc to hundreds of Mpc and from z = 2 up to z = 6 (for a review see Meiksin Reference Meiksin2009). The idea behind the cosmological applications of the Lyα forest is to relate flux fluctuations,
The use of Lyα forest data to probe matter clustering has been pioneered by Croft and co-workers at the end of the 90s: a measurement of the linear matter power spectrum at small scales and high redshift has been presented in Croft et al. (Reference Croft, Weinberg, Bolte, Burles, Hernquist, Katz, Kirkman and Tytler2002), by using high and medium resolution quasar spectra together with the so-called ‘effective bias’ method, P F(k) = b 2 eff(k, z) × P lin(k), that allowed an inversion of the one-dimensional (1D) flux power to infer the underlying matter power spectrum. After that, Viel et al. (Reference Viel, Haehnelt and Springel2004) used a set of about 30 high-resolution high signal-to-noise quasar spectra taken with the UVES/VLT spectrograph and a suite of full hydrodynamic simulation, that explored several thermal histories, to derive the matter clustering at z ~ 2.1 and z ~ 2.7. These data have been combined in a series of paper with WMAP data in order to probe the long-lever arm of the matter power spectrum and get constraints on the running of the spectral index and inflationary parameters (Viel, Haehnelt & Lewis Reference Viel, Haehnelt and Lewis2006). A new era in the Lyα forest field has entered with the advent of the SDSS survey that has allowed to obtain the 1D flux power spectrum from a set of 3 000 low-resolution quasars in the range z = 2.2 − 4.2 over two decades of wavenumbers (McDonald et al. Reference McDonald2005) and to infer the linear matter power spectrum amplitude, slope, and curvature at z = 3 and at a comoving scale of about ~8 Mpc h−1 with unprecedented precision (McDonald et al. Reference McDonald2005), by means of approximate hydro simulations. Again the SDSS data have been combined with other large-scale structure probes to get very tight constraints in terms of neutrino mass fractions and cosmological parameters like running of the spectral index and inflation (Seljak et al. Reference Seljak, Slosar and McDonald2006b). More recently, BOSS/SDSS-III has measured the three-dimensional (3D) clustering of the flux by exploiting the signal in the transverse direction from a set of 50000 quasar spectra: this new data set has allowed to measure at high significance the presence of baryonic acoustic oscillations (BAO) at z ~ 2.2 (Busca et al. Reference Busca2013; Slosar et al. Reference Slosar2013) and a new measurement of the 1D flux power has also been recently provided (Palanque-Delabrouille et al. Reference Palanque-Delabrouille2013).
Lyα forest data are currently providing the tightest constraints in terms of WDM properties and there are two main reasons for this. First of all, the 1D power spectrum is a projection of the 3D one and contains information down to very small scales,
In Table 1 we present a summary of the constraints, in terms of the mass of a thermal relic, that have been obtained by using Lyα forest data.
Table 1. Summary of the constraints obtained on the mass of a WDM relic by using Lyα forest data. Apart from Narayanan et al. (Reference Narayanan, Spergel, Davé and Ma2000) all the other quoted values are 2σ confidence level obtained in a Bayesian analysis.

The first constraint was obtained by Narayanan et al. (Reference Narayanan, Spergel, Davé and Ma2000): by using N-body simulations only and a set of eight high-resolution spectra, the authors looked also at the flux probability distribution function and not just at the flux power and obtained a lower limit of 0.75keV. The main limitations of this work were due to the fact that no hydro simulations were used and a proper marginalisation over nuisance parameters was not done. Viel et al. (Reference Viel, Lesgourgues, Haehnelt, Matarrese and Riotto2005) used instead the effective bias method of Croft et al. (Reference Croft, Weinberg, Bolte, Burles, Hernquist, Katz, Kirkman and Tytler2002) and a set of full hydro simulations to explore the bias in WDM scenarios using high-resolution UVES spectra at z = 2.1, 2.7. In this case, the authors found a 2σ lower limit of 0.55keV for a thermal relic and the nuisance parameters were accounted for (and marginalised over) by allowing an extra normalisation error on the data. In this paper, the authors also quote a 2σ lower limit of 2keV for a sterile neutrino in the so-called Dodelson-Widrow scenario (Dodelson & Widrow Reference Dodelson and Widrow1994) and an upper limit for a gravitino of 16 eV 2σ C.L. in a model for which this particle is not the total amount of DM. Subsequently, Seljak et al. (Reference Seljak, Makarov, McDonald and Trac2006a) exploited the unique capabilities of the SDSS flux power spectrum of McDonald et al. (Reference McDonald2005) (about 3 000 low-resolution low signal-to-noise QSO spectra spanning the redshift range z = 2.2 − 4.2) and showed that the constraints derived from this data set were much tighter due to the wide redshift range probed that allowed to break the degeneracies between cosmological and thermal/nuisance parameters. They obtained a limit of m wdm > 2.5(14)keV for a thermal relic (sterile neutrino) at the 2σ C.L. The analysis made was based on a set of approximate hydro simulations that however explored fully the multi-dimensional likelihood space. The numbers derived above found confirmation in an independent analysis of the SDSS data made by Viel et al. (Reference Viel, Lesgourgues, Haehnelt, Matarrese and Riotto2006) in which a suite of full hydro-dynamical simulations were used at the expenses of a relative poor scanning of the multi-dimensional likelihood space obtained with a Taylor expansion of the flux power. In this work, the limits found were: m wdm > 2(10)keV for a thermal relic (sterile neutrino) at the 2σ C.L., in good agreement with the analysis of Seljak et al. (Reference Seljak, Makarov, McDonald and Trac2006a).
After this Viel et al. (Reference Viel, Becker, Bolton, Haehnelt, Rauch and Sargent2008), explored the very high redshift regime by using 55 high-resolution Keck spectra at z = 2 − 6.4 and obtained the limits m wdm > 1.2(5.6)keV for a thermal relic (sterile neutrino) at the 2σ C.L. However, these limits greatly improved by adding the SDSS data that allowed to break the degeneracies between thermal and WDM cut-offs. A colder (hotter) IGM will result in an increase (suppression) of the flux power due to the thermal broadening of the lines, which is different: this ‘thermal’ effect could either erase or boost the WDM-induced suppression. The advantage of having a wide redshift range allows to appreciate the different redshift evolution of the WDM and thermal cut-offs and to lift or break their mutual degeneracies. Thanks to their constraining power, these data allowed to obtain m wdm > 4.5(28)keV for a thermal relic (sterile neutrino) at the 2σ C.L. In this analysis a second-order Taylor expansion of the flux was used, but again the parameter space was not explored fully and large numerical corrections were made to the flux power in the highest redshift bins.
In Viel et al. (Reference Viel, Becker, Bolton and Haehnelt2013a) these numbers have been revised by using a very comprehensive grid of hydro simulations that embrace a conservative range of different thermal history. At these high redshift it is also likely that galactic feedback and astrophysical effects have a much weaker impact in terms of flux power (Viel, Schaye & Booth Reference Viel, Schaye and Booth2013b). In this case the marginalisation over nuisance parameters has been made fully in the most relevant parameter space and hydro simulations at higher resolutions have been employed. The data used were the highest redshift Keck spectra complemented by an equal number of MIKE (Magellan spectrograph) at poorer resolution. The flux power spectrum has been measured at z = 4.2, 4.6, 5, 5.4 down to the scales of k ~ 0.1 s km−1, roughly corresponding to (very non-linear) scales λ = 50 h − 1Mpc . The final results, that also allow for a conservative extra error on the data side of about 30% and is not sensitive to continuum fitting uncertainties, give m wdm > 3.3keV for a thermal relic at the 2σ C.L., after having marginalised over nuisance, ultra-violet fluctuations, instrumental resolution, and noise of the spectrograph. From this data set and analysis the authors concluded that thermal relics of masses 1keV, 2keV, and 2.5keV are disfavoured by the data at about the 9σ, 4σ, and 3σ C.L., respectively (see Figure 11). WDM models where there is a suppression in the linear matter power spectrum at (non-linear) scales corresponding to k = 10 hMpc− 1, which deviates more than 10% from a ΛCDM model, are disfavoured by the data. Given this limit, the corresponding ‘free-streaming mass’ below which the mass function may be suppressed is ~2 × 108 h −1 M⊙. There appears thus to be very little room for a contribution of the free-streaming of WDM to the solution of what has been termed the small-scale crisis of CDM.

Figure 11. One-dimensional flux power spectrum in dimensionless units (Δ2(k) = P F(k) × k/(2π)) for the SDSS (McDonald et al. Reference McDonald2005) and MIKE+HIRES (Viel et al. Reference Viel, Becker, Bolton and Haehnelt2013a) data sets. These data points span z = 2.2 − 5.4, a period of about 2Gyrs and about two decades in wavenumber space. The best fit ΛCDM model is shown as the blue line, while the orange dashed curves are for a WDM model with a m wdm = 2.5keV, which is excluded by the data at very high significance (note that in this case the other parameters have been kept to their best fit values and only m wdm is changed).
These models have been refined further by accounting for the case of a mixed C+WDM model in Boyarsky et al. (Reference Boyarsky, Lesgourgues, Ruchayskiy and Viel2009a), where an analysis of the SDSS and UVES data was presented. In this work the main results were expressed in terms of a non-resonantly produced sterile neutrino and give m NRP > 8keV (frequentist 99.7% confidence limit) or m NRP > 12.1keV (Bayesian 95% credible interval) in a pure WDM model. For the mixed model, they obtained limits on the mass as a function of the WDM fraction (percentage) to be smaller than 60% for any value of the WDM particle mass (frequentist 99.7% confidence limit), while the Bayesian joint probability allows any value of the mass (for m NRP > 5keV) at the 95% confidence level, provided that the fraction of WDM is below 35%, for any value of the WDM particle mass. This limit can be roughly translated into a thermal relic mass and implies that fractions of WDM below 35% can be accommodated only for masses above m wdm > 1.1keV.
In Boyarsky et al. (Reference Boyarsky, Lesgourgues, Ruchayskiy and Viel2009b) a mechanism of resonantly produced sterile neutrino, that occurs in the framework of the νMSM (the extension of the Standard Model with three right-handed neutrinos), is analysed. Here it was shown that their cosmological signature can be approximated by that of mixed C+WDM and for each mass greater than or equal to 2keV, there exists at least one model of sterile neutrino accounting for the totality of DM, and consistent with Lyα and other cosmological data. However, the transfer function for such candidates is quite different from the one of the thermal relic and no direct comparison with thermal masses can be made.
These lower limits seem to be conflicting with the upper limits obtained on the masses of such particles coming from the observations of the cosmic X-ray background and are: m sν < 1.8keV at 95% confidence (Boyarsky et al. Reference Boyarsky, Neronov, Ruchayskiy and Shaposhnikov2006). In fact, in addition to the dominant decay mode into three active neutrinos, the light sterile neutrino can decay into an active one and a photon with the energy E s = m s/2. Thus, there exists a possibility of direct detection of neutrino decay emission line from the sources with big concentration of DM, e.g. from the galaxy clusters (Abazajian, Fuller & Tucker Reference Abazajian, Fuller and Tucker2001). Similarly, the signal from radiative sterile neutrino decays accumulated over the history of the universe could be seen as a feature in the diffuse extragalactic background light spectrum. However, the constraints above assume a very simple model for sterile neutrino production and can be circumvented by considering other models (Boyarsky et al. Reference Boyarsky, Lesgourgues, Ruchayskiy and Viel2009a).
Overall, Lyα offers a unique probe of the matter power spectrum down to very small scales and the tightest constraints in terms of CDM coldness. The most recent constraint m wdm > 3.3 keV is suggesting that the cosmic web as probed by the Lyα forest data is quite cold and the values of WDM masses (0.5 − 1.5keV) that are typically used in order to solve the missing satellite, the cusp-core, and the ‘too-big-to-fail’ problems for the dynamical properties of the most massive dwarf galaxies at low redshift are in strong tension with the limits above.
3.2 Cosmic weak lensing
In order to complement the Lyα constraints on the thermalised DM particle mass, we could look at the cosmological data of sources seen at different redshifts (tomography). An example of such a probe is gravitational lensing, being also the only probe that does not rely on making assumptions about the coupling between dark and luminous objects in that it probes directly the total gravitational potential.
In particular, the weak gravitational lensing induced in the background distribution of distant galaxy images is known as cosmic shear and is only detectable statistically. Cosmic shear is the weak lensing signal that is induced by the 3D distribution of mass in the universe. We wish to describe in this section how to theoretically calculate the weak lensing angular power spectrum, given a 3D DM power spectrum found in the previous sections (see also Bartelmann & Schneider Reference Bartelmann and Schneider2001). We would like to consider theoretical weak lensing power spectra similar to those that could be obtained by future surveys like Euclid (Amendola et al. Reference Amendola2012; Refregier et al. Reference Refregier, Amara, Kitching, Rassat and Scaramella2010) and present the effect of small-scale WDM-induced suppression. This will be useful for making predictions for constraints and measurements as done in Markovič et al. (Reference Markovič, Bridle, Slosar and Weller2011); Smith & Markovič (Reference Smith and Markovič2011); Viel et al. (Reference Viel, Markovič, Baldi and Weller2012).
An approximate shear power spectrum can be calculated from the halo model (Cooray et al. Reference Cooray, Hu and Miralda-Escude2000) and is made up of two terms, analogously to Equation (15), the one-halo (or Poisson) term and the two-halo (or correlation) term where in order to project the matter power spectrum to two-dimension, the small angle (Limber Reference Limber1953; LoVerde & Afshordi Reference LoVerde and Afshordi2008) approximation must be made.
Markovič et al. (Reference Markovič, Bridle, Slosar and Weller2011); Smith & Markovič (Reference Smith and Markovič2011); Viel et al. (Reference Viel, Markovič, Baldi and Weller2012) considered how to measure the WDM particle mass using observations of cosmic shear power spectra. From an observer's point of view, the image of each galaxy is distorted by gravitational lensing effects of all intervening matter. Therefore, the cosmic shear power spectra are closely related to the matter power spectrum integrated over redshift. Future surveys are expected to use broadband photometry to estimate the redshifts of the observed galaxies. This should allow shear power spectra to be calculated at different redshifts, and also allow cross power spectra between redshifts (see Csabai et al. Reference Csabai2003, for a review).
The above-mentioned halo model approach assumes all sources at the same redshift for simplicity; however, we can expand the calculations to have a source redshift distribution and divide the source galaxies into redshift-determined tomographic bins. We may consider a cosmic shear survey that has a number of galaxies per unit redshift (Smail, Ellis & Fitchett Reference Smail, Ellis and Fitchett1994):
The lensing power spectra are related to the 3D non-linear matter power spectra via
In order to assess detectability of WDM by future weak lensing surveys, the works above calculate predicted error bars on the weak lensing power spectrum using the covariance matrix formalism (Takada & Jain Reference Takada and Jain2004) and assuming errors for a future realistic weak lensing survey with eight redshift bins in the range z = 0.5 − 2.0 (see Figure 12). They additionally consider models of non-linear WDM structure to calculate the weak lensing power spectra. They find that for a survey like Euclid it seems to be sufficient to model the non-linearities using the Halofit prescription of Smith et al. (Reference Smith2003). The limits they predict for the WDM particle mass are at the same order of magnitude as those obtained from Lyα data Section 3.1 and therefore, they hold the potential to confirm the exclusion of m wdm ≲ 2keV. In Table 2, we quote the actual predictions made. We note that a combination of Lyα and weak lensing can also be very promising in constraining the small-scale clustering of matter as done in Lesgourgues et al. (Reference Lesgourgues, Viel, Haehnelt and Massey2007) for a standard CDM scenario.
Table 2. Summary of the forecasts for the Euclid survey for constraining m wdm. The lower limits are quoted to 68% confidence; the fiducial model has been chosen as CDM (i.e. m wdm → ∞).


Figure 12. We plot the ratios between the weak lensing power spectra obtained from a Euclid-type survey. We plot the ratios of the cross-spectra of two tomographic bins, where we have used the Viel et al. (Reference Viel, Markovič, Baldi and Weller2012) fit for the WDM power spectrum from simulations for two different WDM models. The solid lines are the cross- and auto-correlation lensing power spectra. The dotted lines correspond approximately the l fs, i.e. the multipole value corresponding to the free-streaming scale, k fs, at the redshift or the bin (or the closer bin in the case of cross-spectra).
4 CONCLUSIONS
This review has focussed on different approaches for modelling the non-linear structures in our universe in the ΛWDM model and on the possibilities of constraining such a scenario with two particular sets of data: Lyα forest and cosmic shear. We have made a simple choice for the WDM particle: a thermal relic with a ~keV mass, a mass that had been proposed in the past to solve the so-called small-scale crisis of the standard ΛCDM cosmology.
We have decided to rely on a number of assumptions. Firstly, in the modelling of non-linear structure, we have neglected the contributions of baryonic processes (although they have been discussed) to the shape of the potential wells of haloes. We have also focussed more on the clustering of DM and less so on the profiles and substructures of individual DM objects.
Secondly, in types of observations we concentrated on Lyα forest and gravitational lensing and have not discussed for example other promising observables like the 21 cm line (see Sitwell et al. Reference Sitwell, Mesinger, Ma and Sigurdson2013) or the small-scale clustering of galaxies.
Thirdly, we drastically narrowed down the range of possible particle models of DM, allowing only for the particle mass (and therefore temperature) to vary, neglecting non-neutrino-like interactions and particle properties. We have made these choices in order to simplify the analysis. Any possibilities that were neglected here were omitted for reasons of practicality rather than plausibility or usefulness.
In summary, in order to describe a WDM regime, it is crucial to model the non-linearities in the matter power spectrum: thus, we have quoted the results of N-body numerical simulations and described the modifications to the existing halo model. In particular, we have reported on simulations that resulted in a new WDM transfer function for the non-linear power. This fitting function is useful for calculating theoretical WDM power spectra and comparing them to large-scale structure data. We have also touched upon the subject of baryonic physics, modelled by hydro-dynamical simulations. Even though such numerical prescriptions are yet uncertain, it is clear that before a measurement or constraint on the WDM mass is made, one must correctly model baryonic effects.
A possibility to disentangle cosmological and astrophysical effects and to break this degeneracy, could be to look at their potentially different redshift evolution. Whereas the WDM suppression increases with increasing redshift, the effect of baryons may have an entirely different signature. This would be important to model using numerical methods, but it would be a large undertaking as it would require extensive computational resources.
Another powerful tool for understanding and interpreting the large-scale structure is offered by the halo model. The halo model has now been modified and calibrated against N-body simulations such that it is appropriate to use in the ΛWDM cosmology to predict the statistics of the large-scale structure. The new ‘warm’ halo model can be useful for a comparison with future galaxy surveys, where in order to compare the galaxy distribution measured from observations, one must populate the theoretical DM density field with galaxies. This WDM halo model has been developed with a rather physical motivation by Lesgourgues & Tram (Reference Lesgourgues and Tram2011) constructing the density field from DM haloes that host galaxies. We have not discussed the clustering of galaxies explicitly, because competitive constraints should come only from small scales where the interpretation is not trivial and should rely on halo occupation distribution models. Therefore we have found it sufficient and more promising in terms of future detectability to focus on weak lensing.
We have also shown the Schneider et al. (Reference Schneider, Smith, Maccio and Moore2012) rescaling of the mass functions with respect to the ‘half-mode mass’ and found that this resulted in power spectra that matched the N-body simulations well. However, the lack of a prescription for how this rescaling varies with redshift makes it more difficult to use in comparing models to data. It is likely that other prescription for the mass function (e.g. Angulo et al. Reference Angulo, Hahn and Abel2013; Pacucci et al. Reference Pacucci, Mesinger and Haiman2013; Schneider et al. Reference Schneider, Smith and Reed2013b) will be more appropriate. Also for this reason, the fitting function to the final power spectra found by Viel et al. (Reference Viel, Markovič, Baldi and Weller2012) describes the redshift evolution of the WDM suppression better.
We have summarised the recent results coming from the Lyα forest data, which still provide the strongest constraints to date, of 3.3keV at 2σ confidence (Viel et al. Reference Viel, Becker, Bolton and Haehnelt2013a). We have summarised forecasts for future large-scale structure surveys, in particular for the Euclid weak lensing survey. This was done in order to show how the free-streaming of WDM, which smoothes out the sub-0.1Mpc scales in the linear density field impacts the present day measurements of cosmic shear. These forecasts have indicated that the constraints that could be placed on the m wdm parameter, i.e. the ‘warmth’ of DM, from cosmic shear will be comparable, but not stronger, than those coming from Lyα. In other words, because the Lyα forest probes cosmic times in the past that are much closer to the linear regime than today and is a projected measurement of the 3D density field, it has the most constraining power in measuring the small-scale suppression coming from the WDM free-streaming, although the redshift range probed is very different from other observables.
The forecasts for Euclid show that WDM particles with masses of the order of m wdm ~keV have a large enough impact on the non-linear density field to be detectable. It should be noted that interesting constraints on the coldness of CDM can also be placed by using the properties of individual objects (galaxies, DM haloes, GRBs, etc.) and have been presented by many authors. Future and present surveys like Planck, SDSS and Euclid, SKA, and E-ELT will also help in measuring the small-scale properties of the large-scale structure and place stronger constraints in terms of the mass of the DM particle.
As mentioned above, WDM is not the only model able to alter the ΛCDM cosmology on small scales. It has become clear in the past decade, through the works described in this review, among others, that the present non-excluded models of ‘standard’ WDM are on the limit of detectability and are, because of the increasingly tighter constraints on them, less able to alleviate the small-scale issues of ΛCDM than initially hoped for. As this review was being written, other authors have started to come to the same conclusions (e.g. Schneider et al. Reference Schneider, Anderhalden, Maccio and Diemand2013a; Kennedy et al. Reference Kennedy, Frenk, Cole and Benson2013). Luckily, there remain other types of DM models, alternative to the standard WIMP scenario, for example decaying or self-interacting DM that are also promising and worth to investigate.
5 ACKNOWLEDGEMENTS
KM and MV thank their colleagues involved in WDM topics that helped collecting the material for this review and in particular Sarah Bridle, Anže Slosar, Marco Baldi, Jochen Weller, Martin Hahnelt, George Becker, and James Bolton. KM acknowledges support from project TRR 33 ‘The Dark Universe’. MV is supported by the FP7 ERC Grant ‘cosmoIGM’ GA-257670 and the INFN/PD51 grant.

















