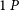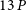Investigation of mode changing of PSR J1921+1419 with FAST

Abstract

The single pulses of PSR J1921+1419 were examined in detail using high-sensitivity observations from the Five-hundred-meter Aperture Spherical radio Telescope (FAST) at a central frequency of 1250 MHz. The high-sensitivity observations indicate that the pulsar exhibits two distinct emission modes, which are classified as strong and weak modes based on the intensity of the single pulses. In our observations, the times spent in both modes are nearly equal, and each is about half of the total observation time. The minimum duration of both modes is $1\,P$ and the maximum duration is $13\,P$, where P is the pulsar spin period. Additionally, the mean intensity of the weak mode is less than half of that of the strong mode. Notably, the switching between these modes demonstrates a clear quasi-periodicity with a modulation period of approximately $10 \pm 2\,P$. An analysis of the polarisation properties of both modes indicates that they originate from the same region within the magnetosphere of the pulsar. Finally, the viewing geometry was analysed based on the kinematical effects.

1. Introduction

Pulsars are rapidly rotating and highly magnetised neutron stars. To date, over three thousand pulsars have been discovered. ^a As pulsars rotate, they continuously emit single pulses with high periodicity. These pulses exhibit interesting phenomena, such as subpulse drifting (Drake & Craft 1968; Cordes 1975), nulling (Backer 1970a) and mode changing (Backer 1970b). These phenomena reflect the underlying properties of pulsar emission. Although numerous theoretical models have been proposed to explain these observations (e.g. Ruderman & Sutherland 1975; Herfindal & Rankin 2007), the specific mechanisms remain elusive.

Mode changing is the phenomenon where pulse emission switches between two or more emission modes (e.g. Bartel et al. 1982; Basu, Mitra, & Melikidze 2023). Since mode changing was first discovered in PSR B1237+25 (Backer 1970b), its origin has remained a mystery. Increasing evidence suggests that mode changing may be related to changes in the magnetospheric particle current flow (Lyne, Smith, & Graham 1971), but the physical mechanism behind these changes is not yet understood. Numerous observations indicate that mode changing is not always a stochastic process (Basu et al. 2016), as evidenced by the recently reported periodic non-drift amplitude modulation (e.g. Yan et al. 2019, 2020; Zhao et al. 2023).

Nulling refers to the phenomenon where pulse emission suddenly disappears for a series of pulse periods and then suddenly recovers (e.g. Backer 1970a; Burke-Spolaor et al. 2012; Gajjar, Joshi, & Kramer 2012. This usually occurs in relatively old pulsars. Some pulsars are reported to show quasi-periodicity in their nulling behaviour (e.g. Rankin & Wright 2007; Rankin 2008; Herfindal & Rankin 2007, 2009; Rankin, Wright, & Brown 2013; Basu, Mitra, & Melikidze 2017), which is very similar to the periodic non-drift amplitude modulation. Therefore, Basu et al. (2017) suggested that they may have a common physical origin. This supports the viewpoint of Wang, Manchester, & Johnston (2007) that nulling and mode changing are different manifestations of the same phenomenon.

PSR J1921+1419 is a pulsar with mode changing. It was discovered at the Arecibo Observatory in 1974 (Hulse & Taylor 1974), with a spin period of 0.618 s, dispersion measure of 91.64 pc cm $^{-3}$ , characteristic age of 1.75+10 $^6$ yr, and magnetic field of 1.88 + 10 $^{12}$ G (Hobbs et al. 2004a; Manchester et al. 2005). Lyne & Manchester (1988) analysed the profile and polarisation of PSR J1921+1419 and suggested that its emission beam was cone-dominated. Rankin (1993a) showed that the profile of PSR J1921+1419 presents the core component, but the core component is not clearly discernible at any frequency. Song et al. (2023) used MeerKAT to analyse the modulation behaviour of intensity for PSR J1921+1419 and found that the period of intensity modulation is about 10 P, where P is the pulsar spin period.

Some satisfactory results were obtained in the previous studies about PSR J1921+1419, but detailed studies of single pulses are lacking. High-sensitivity observations have the potential to uncover more detailed information. Previously, the Five-hundred-metre Aperture Spherical radio Telescope (FAST) with high sensitivity has observed peculiar phenomena that many other telescopes could not detect (e.g. Zhi et al. 2023; Xu et al. 2024a, b). In this paper, we will study the single-pulse behaviour of PSR J1921+1419 based on the high-sensitivity telescope FAST, aiming to discover more details. This paper is structured as follows: Section 2 details the observations of this pulsar with FAST and the associated data reduction methods. Section 3 presents the analysis and results for this pulsar. Section 4 provides discussions and conclusions.

2. Observations and data processing

On November 7, 2023, we conducted an about 40-min observation of PSR J1921+1419 utilising FAST with high sensitivity. This observation was carried out using the central beam of the 19-beam receiver, covering a frequency range from 1 000 to 1 500 MHz. Due to the effect of frequency band edges, we restricted our analysis to data within the frequency range of 1 050–1 450 MHz (Jiang et al. 2020). The data was recorded in search mode PSRFITS format (Hotan, van Straten, & Manchester 2004) using full-Stokes information, 8-bit samples, a 49.152 ${\mu}$ s time resolution, and 4 096 frequency channels. With the timing ephemeris provided by Australia Telescope National Facility (ATNF) pulsar catalogue (PSRCAT V-1.67) (Manchester et al. 2005), we used the software package DSPSR (Hotan et al. 2004; van Straten & Bailes 2011) to fold data at 1 024 phase bins per pulse period and obtained single pulse profiles. We obtained a total of 4 147 individual pulses. The narrow-band radio frequency interference (RFI) in observation was flagged and removed by using the PAZ command of the PSRCHIVE software package (Hotan et al. 2004; van Straten, Demorest, & Oslowski 2012. Thanks to FAST’s excellent observing environment, our observations were minimally affected by RFI. The polarisation calibration was realised with the noise signal using the PAC command of the PSRCHIVE software package. We used the RMFIT command of the PSRCHIVE software package to fit the Faraday rotation measure (RM) and obtained RM = 166.72 $\pm$ 1.54 rad m $^{-2}$ , which is consistent with the results from Han et al. (2018) within the error range.

3. Results

Our high-sensitivity observations of PSR J1921+1419 revealed intricate details of its single pulse features, with prominent mode changing being the primary distinctive phenomenon of this pulsar. The results are depicted in Fig. 1, showing a stacked diagram of 200 consecutive single pulses. In this section, we will provide a detailed account of these single pulse characteristics.

Figure 1. The single-pulses stack diagram of 200 successive single pulses from PSR J1921+1419 is obtained by using FAST observed at 1 250 MHz central frequency. The single-pulse intensity is reflected by the extent of both brightness and darkness. The time extends from left to right through pulses and successive pulses are plotted from bottom to top. The intensity of the single pulse regularly varies with time.

3.1. Identification of mode changing

To distinguish between the two emission modes, we employed the method proposed by Miles et al. (2022) for identifying them. Firstly, we measured the signal-to-noise ratio (S/N) of every single pulse from PSR J1921+1419 based on the expression,

(1) \begin{align} S/N = \frac{S - N \cdot \mu}{{\sigma}_n \cdot \sqrt{N}}, \end{align}

where S is the integrated intensity within the on-pulse window, N is the number of longitude phase bins, and $\mu$ as well as ${\sigma}_n$ are the mean and standard deviation for the off-pulse region. This expression seems to be more suitable for the study of shape variations between pulses and can get a more accurate S/N for weak emission pulses. Then, the probability distribution function (PDF) of S/N is defined as Equation (5) of Miles et al. (2022).

With Bayesian parameter estimation, we modded S/N probability distribution for PSR J1921+1419, and the results are plotted in Fig. 2. The left panel shows the posterior distributions of the parameter estimate. It can be seen that all the parameters except ${\alpha}_1$ converge very well. The right panel displays the histogram of S/N density overlaid with the PDF and the two modes deconvolved from a Gaussian distribution characterised by parameters $\mu_n$ = 0 and $\sigma_n$ = 3.1, where $\mu_n$ and $\sigma_n$ were obtained by fitting noise S/N distribution. As expected, the PDF (green) deconvolved from the observed noise shows a bimodal distribution.

Figure 2. Left panel: The posterior distributions of the parameter estimate of the S/N distribution for PSR 1921+1419. Right panel: the probability density histogram of S/N for PSR J1921+1419 all single-pulses, including the curve line fitted using convolution model (red), the same fit deconvolved from the observed noise (green), and the strong (blue) and the weak (orange) modes.

Figure 3. The S/N sequence of the same pulses (upper panel) as in Fig. 1 with the corresponding identified strong/weak mode (lower panel). In the upper panel, a red dot is the on-pulse S/N of a given pulse and the green line represents the threshold level of the single-pulse S/N. Pulses for which pulse S/N below the green line were tagged as the weak-mode pulses and pulses above the green line were tagged as the strong-mode pulses.

3.2. Emission properties

According to the PDF of the two modes, the S/N threshold of the two modes is determined to be 19.57, corresponding to a value that the probability of a weak-mode pulse appearing in the strong-mode distribution is marginal ( $ \lt $ 0.01%). Therefore, the pulses with S/N $\leq$ 19.57 are classified into the weak mode and pulses with S/N $ \gt $ 19.57 into the strong mode. In Fig. 3, we presented the results of the mode separation of 200 successive single pulses. Our results indicate that PSR J1921+1419 spends nearly equal amounts of time in both emission modes, with each mode accounting for approximately half of the total observation time.

For most pulsars with mode changing, the emission switches between modes with varying timescales, which is important to study the pulsar emission mechanism. In Fig. 4, we displayed the duration distributions of both strong and weak modes. It can be seen that, whether it is strong or weak modes, the frequency of the occurrence is the highest when the duration is 1 P. The maximum duration of both modes is 13 P.

Figure 4. The duration distribution of the strong and the weak modes for PSR J1921+1419.

It is evident from Fig. 1 that switches between the modes show a quasi-periodicity. To analyse this periodicity further, we used the method proposed by Basu et al. (2017). Firstly, the weak-mode pulses and the strong-mode pulses were identified as time series data of ‘0’ and ‘1’, respectively. This step is for all subpulse information to be washed, ensuring that the obtained modulation period comes from switching between the modes. Then, we carried out a one-dimensional discrete Fourier transform (DFT) for the consecutive time series having a total length of 256. The starting position was continuously shifted by 10 pulse periods, and the process was repeated until the time series data ended. Finally, all individual DFTs were averaged to obtain the period in switches between the modes. Fig. 5 shows the time-varying Fourier transform of the strong/weak (1/0) time series data for PSR J1921+1419. A clear periodic feature with a peak frequency at 0.10 $\pm$ 0.05 cycles period $^{-1}$ was shown in Fig. 5. Here, the uncertainty is calculated by FWHM/2 $\sqrt{2 {\ln(2)}}$ (Basu et al. 2016), where FWHM was the full width at 50% intensity for the peak feature. The corresponding modulation period is roughly 10 $\pm$ 2 P, which is consistent with the intensity modulation period obtained by Song et al. (2023).

Figure 5. Left panel: The time series data of the weak-mode and the strong-mode pulses identified as ‘0’ and ‘1’, respectively. Main panel: The time-varying Fourier transform corresponding to the time series data. Lower panel: The average Fourier transform over the time series data.

3.3. Polarisation

In order to compare the emission nature of the strong and weak modes further, we analysed the polarisation properties of the strong and weak modes. We showed the polarisation profiles of the average of all pulses, strong-mode pulses, and weak-mode pulses in Fig. 6, and gave a summary of those profiles in Table 1. Columns (2) and (3) listed the linear polarisation fraction ${\langle}L{\rangle}/I$ and the net circular polarisation fraction ${\langle}V{\rangle} /I$ , respectively. Here, I is the mean of total intensity within the on-pulse window, ${\langle}{\rangle}$ means an average across the on-pulse window. The last two columns give the pulse widths, at 10% of the peak flux density, $W_{10}$ , and 50% of the peak, $W_{50}$ , respectively. The uncertainties of $W_{10}$ and $W_{50}$ are calculated by equation ${\sigma}\,=\,res\,\sqrt{1\,+\,(rms/I)^2}$ (Olszanski, Mitra, & Rankin 2019), where res is the time resolution, rms is the standard deviation of the off-pulse region, and I is the measured average signal intensity across the on-pulse window. These results obtained via us are consistent with the results of previous studies within the limits of error (Hobbs et al. 2004b; Wang et al. 2023).

Table 1. The parameters of strong and weak modes for PSR J1921+1419.

Figure 6. The polarisation profiles of the average over all pulses (left-hand panel), the strong-mode pulses (central panel), and the weak-mode pulses (right-hand panel) from PSR J1921+1419 at 1 250 MHz. The total intensity (Stokes I, black solid liner), total linear polarisation (Stokes $L = \sqrt{Q^2+U^2}$ , red dashed line), and circular polarisation (Stokes V, blue dashed line) are given in the lower panel. The horizontal bar in the left-lower panel shows the preferred position and range of the fiducial plane considered. In the upper panel, the black dots with error bar are PA ( $\psi\,=\,\frac{1}{2}\,\tan^{-1}\,(U/Q)$ ) of the corresponding polarisation profile, the red curve is the best result using RVM to fit PA, and the green dots with error bars are PA of average profile.

As shown in Fig. 6, the polarisation profile of the average pulse profile is consistent with the result in Wang et al. (2023). The average pulse profile is formed by overlapping multiple emission components (Rankin 1993a). For the polarisation profile of the strong mode, both the leading and the trailing edges are depolarised, and the peak positions of the linear polarisation profile approach the shoulder components. However, for the polarisation profile of the weak mode, only the leading edges are depolarised, and the peak position of the linear polarisation is in the peak component of the profile. Compared to the strong mode, the swing of the circular polarisation curve for the weak mode is moderate. It is also noted that the mean intensity of the weak mode is less than half of that of the strong mode.

In Fig. 6, we also showed the linear polarised position angle (PA) corresponding to the average profile, strong mode profile, and weak mode profile within the on-pulse window. It can be seen that their PA curves almost overlap, and are all swing of S-shaped. This S-shaped swings can be well explained with the rotating vector model (RVM) proposed by Radhakrishnan & Cooke (1969). According to the RVM model, the PA ( $\psi$ ) is defined as a function of the pulse longitude ( $\phi$ ):

(2) \begin{align} \tan \big ( \psi - \psi_0 \big ) = \frac{\sin \alpha \sin \big (\phi - \phi_0 \big )}{\sin \zeta \cos \alpha - \cos \zeta \sin \alpha \cos (\phi -\phi_0)},\end{align}

where $\alpha$ is the inclination angle between the magnetic axis and the rotation axis; $\zeta = \alpha + \beta$ is the angle between the line-of-sight and the rotation axis, $\beta$ is the impact parameter, namely, the angle between the line-of-sight and the magnetic axis at the position of closest approach; $\psi_0$ and $\phi_0$ are the PA and pulse longitude, respectively, of the steepest dot of this PA curve. The red curve in Fig. 6 upper panel is the best result using the RVM model to fit the PA. The corresponding $\psi_0$ and $\phi_0$ are listed in Columns (3) and (4) of Table 1, respectively. The $\psi_0$ obtained by us is consistent with the results published by Wang et al. (2023) within the limit of error. It can be known that the positions of the steepest dot obtained by these fits are the same within the error range and have been all well constrained. However, the $\alpha$ and $\beta$ values obtained by this method have great uncertainty because $\alpha$ and $\beta$ are covariant and the proportion of the emission window in the pulse period is limited (Mitra & Li 2004). We will analyse the values of $\alpha$ and $\beta$ further below.

3.4. Possible viewing geometry

It is difficult to accurately measure viewing geometry ( $\alpha$ and $\beta$ ) for pulsars. Usually, we can only constrain the viewing geometry of pulsars. For this pulsar, the PA curves of both strong and weak modes almost overlap with that of the average profile, which means that the emission of the two modes comes from the same magnetospheric region. Therefore, next, we will consider the viewing geometry for PSR J1921+1419 based on its average pulse profile and corresponding shape of the PA swing.

To derive the viewing geometry from the shape of the PA swing, the reduced chi-square ( $\chi^2$ ) of fitting an RVM curve for each ( $\alpha,\beta$ ) combination for the average profile was calculated and is shown in Fig. 7.

Figure 7. The results of fitting an RVM curve for each ( $\alpha, \beta$ ) combination for the average profile. The reduced $\chi^2$ of the fit is shown as the blue scale. The red contours correspond to the 1 $\sigma$ , 2 $\sigma$ , 3 $\sigma$ confidence boundaries. The grey region shows constrained viewing geometries allowed by the observed pulse width.

The RVM predicts that the inflection point (the steepest dot of the PA curve) coincides with the passage of the line-of-sight through the fiducial plane, the plane containing both the rotation and the magnetic axes (Rookyard, Weltevrede, & Johnston 2015). In the actual observation of pulsars, the inflection point predicted by using RVM to be delayed relative to the position of the fiducial plane as inferred from the intensity profile ( $\phi_{fid}$ ), and the delay is calculated by $\Delta \phi = \phi_0 - \phi_{fid}$ . This delay is caused by the relativistic effects known as aberration (A) and retardation (R) as a result of pulsar rotation. The range and most likely value of $\phi_0$ can be estimated by fitting the PA (see Table 1). The $\phi_{fid}$ is obtained based on profile morphology. The horizontal bar above the total intensity curve in the left-lower panel of Fig. 6 displays the preferred value and range of the $\phi_{fid}$ for PSR J1921+1419 ( $\phi_{fid} = 169.81 \pm 4.02^{\circ}$ ). According to Blaskiewicz, Cordes, & Wasserman (1991), using the delay ( $\Delta \phi$ ), the absolute radiation height ( $h_{em}$ ) at the frequency of observation can be calculated by

(3) \begin{align} h_{em} = \frac{Pc \Delta \phi}{8 \pi},\end{align}

where P is the rotation period of the pulsar, c is the speed of light. The derived emission height for PSR J1921+1419 is $h_{em}\,=\,378.49^{+517.10}_{-378.49}$ km. In addition, we also used Eq. (3) of Kijak & Gil (2003) to calculate the emission height of this pulsar ( $h_{em} = 368.58 \pm 77.01$ km). These two results are consistent within the margin of error.

Under the assumptions of both that the radio emission beam is defined as the cone bounded by tangents to the last open field lines at the emission height and that the magnetic field at the pulsar surface is dipolar, the half-opening angle ( $\rho$ ) of the radio emission beam for a pulsar can be calculated by

(4) \begin{align} \rho = \theta_{PC} + \arctan \!\left(\frac{1}{2} \tan \theta_{PC} \right),\end{align}

where $\theta_{PC}$ is the angular radius of the open field-line region, defined as

(5) \begin{align} \theta_{PC} = \arcsin \bigg(\sqrt{\frac{2 \pi h_{em}}{Pc}}\bigg)\end{align}

(Lyne & Graham-Smith 2012). For this pulsar, we obtained $\theta_{PC} = 6.5 \pm 4.46^\circ$ and $\rho = 9.77 \pm 6.72^\circ$ .

Because the half-opening angle of a conical emission beam centred on the magnetic axis is related to $W_{open}$ , the $\alpha$ and $\beta$ can be constrained via the equation

(6) \begin{align} \cos{\rho} = \cos \alpha \cos (\alpha + \beta) + \sin \alpha \sin (\alpha + \beta) \cos{\frac{W_{open}}{2}} \end{align}

(Gil, Gronkowski, & Rudnicki 1984), where $W_{open}$ is the range in the pulse phase for which the line-of-sight samples the open-field-line region. $W_{open}$ is taken to be twice the distance from the $\phi_{fid}$ to the furthest profile edge, where profile edge was taken to be the point at 10% of the peak intensity of the profile (Rookyard et al. 2015). For PSR J1921+1419, we obtained $W_{open}$ = $25.02 \pm 8.03^\circ$ . The possible viewing geometries consistent with the profile width and the delay of the PA curve with respect to the fiducial plane are shown as the grey regions of Fig. 7. Obviously, for this pulsar, its magnetic inclination angle and impact parameter are constrained in the range of $\alpha \gt 118^\circ$ and $-11^\circ \lt \beta \lt 0^\circ$ , respectively.

4. Discussion and conclusions

We analysed the single pulse behaviour of PSR J1921+1419 using FAST. Our results showed that the single pulses of PSR J1921+1419 exhibit two different emission modes, which are strong and weak. In our observations, the times spent in both modes are nearly equal, and each is about half of the total observation time. Both modes show the highest frequency of occurrence when the duration is 1 P. It is also noted that the duration of both modes is not more than 13 P. Additionally, the mean intensity of the weak mode is less than that of the strong mode. It is worth noting that the switch between the modes displays a clear quasi-periodicity with a modulation period of approximately $10 \pm 2$ P. An analysis of the polarisation properties of both modes indicates that they originate from the same region within the magnetosphere of the pulsar. Finally, we constrain the viewing geometry of PSR J1921+1419 based on the kinematical effects.

The radio emission from pulsars is produced by non-linear plasma processes that charged bunches excite coherent curvature radiation along the curved magnetic field. The observed radio intensity is the result of the incoherent summation of emissions from a large number of such charged bunches (Asseo & Melikidze 1998; Melikidze, Gil, & Pataraya 2000; Gil, Lyubarsky, & Melikidze 2004). In this case, the characteristic frequency and power of pulsar emission can be expressed by $\nu_c\,\sim\, \gamma^3c/\rho_c$ and $P\,\propto\,F(Q)\gamma^4/\rho^2_c$ , respectively, where $\gamma$ is the Lorentz factor of the radiating plasma, c is the speed of light, $\rho_c$ is the radius of curvature of the magnetic field and F(Q) has the dimension of charge squared and is a complex function of the plasma parameters. In our work, the PAs of PSR J1921+1419 remain consistent between the two emission modes, which implies that emission geometries of the two modes may be the same, which means $\rho_c$ is unchanged in the different modes. Hence the observed differences in the intensities of the two modes at the same frequency can only occur due to variations in F(Q), which is complicatedly related to the changes in the plasma parameter. The plasma changes are likely driven by variations in the inner acceleration region where they are generated (Basu & Mitra 2018). Therefore, we believe that the difference in intensity between the two modes is caused by the complex plasma processes that take place during plasma generation in the inner acceleration region rather than the different emission regions. Similar conclusions have also been drawn in PSR J1822−2256 (Basu & Mitra 2018). The weak mode has a slightly higher linear polarisation fraction than the strong mode, but the difference in circular polarisation fraction between the two modes is not discernible. Such slight variation in linear polarisation fraction may be associated with changes in plasma inhomogeneity (Melikidze, Mitra, & Gil 2014).

We have used two methods to calculate this pulsar’s emission height. The first method is based on the delay effect due to pulsar rotation. The second method is from Eq. (3) of Kijak & Gil (2003). Two results calculated by these two methods are consistent within the margin of error. Compared to the result calculated by the first method, the result calculated by the second one is with a smaller error. However, the first method is an independent procedure, while the second method is established on three straightforward assumptions. This means the first method is probably more convincing than the second one. We prefer to use the result calculated using the first method. Wang et al. (2023) have also calculated this pulsar’s emission height by the first method. Within the margin of error, our results are consistent with theirs.

Magnetic inclination angle is one of the important parameters of pulsars, and it is not easy to obtain the accurate value of the magnetic inclination angle for most pulsars. Ken’ko & Malov (2023) have carried out a large sample analysis of the evolution of the magnetic inclination angle. In their study, the magnetic inclination angle of PSR J1921+1419 was obtained, with $\alpha = 9.2^\circ$ . There is a big difference between our results and this one. Ken’ko & Malov (2023)’s result was obtained based on the statistical dependence of $W_{10}$ on the period and the assumption that the line of sight passes through the centre of the pulsar’s emission cone (the impact parameter $\beta = 0^\circ$ ). The value calculated by this method is less than the real magnetic inclination angle for most pulsars, only represents the lower limit of the magnetic inclination angle. Our result is calculated based on the kinematical effects of pulsar rotation and the 3 $\sigma$ confidence boundary of $\chi^2$ of the RVM fitting, without limiting the impact parameter. This method is general for most pulsars and is used in many studies (e.g. Xu et al. 2024a; Dang et al. 2024). Hence, our result is more general and reliable, and the difference between magnetic inclination angles obtained by us and by Ken’ko & Malov (2023), may be caused by the fact that they have used the statistical dependence of $W_{10}$ on the period and an assumption, $\beta\,=\,0^\circ$ . Additionally, the impact parameter $\beta$ we obtained is negative, while that obtained by Wang et al. (2023) and that obtained by Johnston et al. (2023) are positive. This is caused by the fact that we use the definition of the normal RVM, where PAs increase clockwise on the sky, whereas they use the so-called ‘observer’s convention’, which defines PAs as increasing counter-clockwise on the sky.

With the increase in pulsar observation data, the periodic phenomena are observed in the radio emission of more and more pulsars, such as subpulse drifting (Weltevrede, Edwards, & Stappers 2006; Zhi et al. 2023; Xu et al. 2024b), the periodic non-drift amplitude modulation (Mitra & Rankin 2017; Yan et al. 2019), and periodic nulling (Basu et al. 2017). Basu, Mitra, & Melikidze (2020a) analysed these phenomena in detail. They found that there is a dependent relationship between the subpulse drifting phenomenon and the spin-down luminosity $\dot E$ . The subpulse drifting is only detected in pulsars with $\dot E \lt 2 \times 10^{32}$ erg s $^{-1}$ , and drifting periodicity is anticorrelated with $\dot E$ . However, both periodic nulling and non-drift amplitude modulation can be detected in pulsars with larger $\dot E$ , and their modulation periodicity is not correlated with $\dot E$ . The spin-down luminosity for PSR J1921+1419 is $\dot E = 9.36 \times 10^{32}$ erg s $^{-1}$ (Song et al. 2023), and thus PSR J1921+1419 is classified in the non-drift amplitude modulation group.

According to the studies of Rankin (1983, 1990, 1993b), the radio emission beam for pulsars is comprised of a central core emission surrounded by conal emission arranged in nested rings. The number of the pulse profile components is related to the line-of-sight across the emission beam. Based on this model, Basu et al. (2020a) found that, the subpulse drifting phenomenon is detected only in the cone component with pulsars of absent core component, while both periodic nulling and periodic non-drift amplitude modulation can be detected across the entire pulse window in the cone and core components simultaneously. PSR J1921+1419 is the cone-dominated pulsar (Lyne & Manchester 1988), but in its pulse profile, the core component exists (Rankin 1993a). It can be seen from Fig. 1 that non-drift amplitude modulation is detected in all components of PSR J1921+1419. This result follows the conclusion of Basu et al. (2020a).

Considering the similarities between periodic non-drift amplitude modulation and periodic nulling, some researchers suggested that they have a common physical origin (e.g. Basu et al. 2017; Basu, Mitra, & Melikidze 2020b). Some researchers claim that the periodic nulling can be explained using the rotating subbeam carousel model (Herfindal & Rankin 2007), in which the evenly spaced conal subbeams rotate around a central core component. They consider that when the area where the line-of-sight passes is an extinguished subbeam or the empty region between two conal subbeams, nulling occurs, and it can repeatedly occur after certain pulse periods, that is, the missing line-of-sight model. However, in subbeam carousel model, the central core component does not take part in the carousel ${\prime}$ s rotation. So, the periodic nulling observed in pulsars with core components was not adequately explained by the missing line-of-sight model (Basu et al. 2017). In this work, we reported periodic non-drift amplitude modulation of PSR J1921+1419. Both core and cone components switch between strong and weak modes periodically, and the weak mode represents relatively weak emission within the pulse window, rather than the nulling. This result does not fit very well with the missing line-of-sight model.

It is reported in an increasing number of pulsars that the periodic non-drift amplitude modulation is seen in the core component of the pulse profile, such as PSRs B1946+35 (Mitra & Rankin 2017), J0826+2637 (Basu & Mitra 2019), and J1048-5832 (Yan et al. 2020). This phenomenon can not be explained based on the carousel model that can explain subpulse drifting. For PSR J1921+1419 by this work, the periodic non-drift amplitude modulation can also be seen in the core component of its pulse profile. It is believed that periodic non-drift amplitude modulation in PSR J1921+1419 results from similarly periodic fluctuations in the magnetospheric field currents that are not directly related to subpulse drifting. Yan et al. (2020) have also obtained similar conclusions in the study of PSR J1048-5832.