1 INTRODUCTION
To date, more than 3 400 exoplanets in about 2 570 planetary systems have been discovered using different observational techniques. About 10% of these planets are found in stellar systems with two or more stars (Adams et al. Reference Adams2012; Roell et al. Reference Roell, Neuhäuser, Seifahrt and Mugrauer2012; Lodieu et al. Reference Lodieu2014). The stellar multiplicity can alter the dynamical evolution and the orbit of the planets due to the Kozai-Lidov mechanism [hereafter KL; see Kozai (Reference Kozai1962) and Lidov (Reference Lidov1962)] and other phenomena. The KL is a dynamical perturbation in the orbit of a satellite (planet or star) by the gravitational influence of another body on a wider and misaligned orbit. Astronomers are now able to study the differences in the planetary orbital parameters and masses between single and multiple stellar systems. The dynamical study of these stellar systems can shed some light on the possible values for their orbital parameters, increasing the knowledge about exoplanet formation and evolution. For example, the orbital inclination allows us to conclude if the KL is the cause of the high orbital eccentricity observed in planets around stars in multiple systems and the periodic change of the planetary orbital parameters. The eccentricity and semimajor axis allow us to calculate the boundaries of stability within a three body system, which are important parameters to define the orbital planetary stability and stable zones around a stellar component. Hauser & Marcy (Reference Hauser and Marcy1999) studied dynamically the stellar system 16 Cygni analysing the relative astrometry and the orbital parameters for a bound condition. They concluded that the wide stellar component is the cause of the high planetary eccentricity.
GAIA (Global Astrometric Interferometer for Astrophysics) is a European Space Agency (ESA) space astrometry mission launched on 2013 December 19. It is the successor of Hipparcos satellite and will monitor about 1 billion objects down to magnitude 20, during its 5-yr mission. It will provide distances, positions and proper motions with an unprecedented accuracy of 0.02 and 0.20 mas for bright and faint stars (mag ⩽ 19), respectively, as well as radial velocities. GAIA will determine the distances to the nearest objects with accuracy of 0.001%. This extremely accurate astrometric and kinematical data will be a great help in determining orbital parameters of wide binaries using a suitable orbital calculation method and different from those used for close visual binaries. While waiting for GAIA data, it is important to perform dynamical studies and to determine orbital solutions distribution for binary stars hosting exoplanets improving techniques that make use of data obtained from the Earth.
GAIA data can be exploited using the Apparent Motion Parameter (Kiselev & Kiyaeva Reference Kiselev and Kiyaeva1980; Kiselev Reference Kiselev1989), hereafter AMP, or Hauser & Marcy (Reference Hauser and Marcy1999) method for orbital estimations. These techniques only need very accurate instantaneous position (x, y, z) and velocity vectors (
![]() $\mathit {V_x}$
,
$\mathit {V_x}$
,
![]() $\mathit {V_y}$
,
$\mathit {V_y}$
,
![]() $\mathit {V_z}$
) in addition to the masses of the stellar components and a trigonometric parallax.
$\mathit {V_z}$
) in addition to the masses of the stellar components and a trigonometric parallax.
HD 106515 AB (WDS 12151–0715 AB = STF1619 AB = HIP 59743) is a wide binary system that is astrometrically well-sampled and has a high common proper motion (hereafter CPM) which was first observed by de Lalande (Reference de Lalande1831) in 1795. The system is composed of two stars G5/6V and G8/9V with V = 7.96 and V = 8.22 mag, respectively. Since 1795, it has been observed 135 times. During this time, the angular separation and position angle has changed from 8.0 to 6.9 arcsec and from 295° to 266°, respectively. Gould & Chanamé (Reference Gould and Chanamé2004) and Marmier et al. (Reference Marmier2013) based only on the CMP concluded that HD 106515 is composed of stars gravitationally bound. The common radial velocity (RV hereafter) was used by Desidera et al. (Reference Desidera2012) to reinforce the bound status. These are necessary, but in same cases not sufficient conditions. In this work, we add new important evidence (small curvature, common distance, dynamic stability, etc.) to assure the gravitationally bound status.
A planet of nearly 9.6 Jupiter masses was discovered around HD 106515 A by measuring radial velocities (Mayor et al. Reference Mayor2011), with an estimated orbital period of 3 630 d (about 10 yrs), which is one of the largest orbital periods for planets discovered using RV techniques. Desidera et al. (Reference Desidera2012) studied the binary system determining orbital parameters, which allowed them to define the critical semimajor axis as a function of z (and therefore the stable zones around the stars). They suggested that the high eccentricity of the planet could be caused by KL.
In this work, we developed a dynamical and orbital study more complete and detailed than in the literature, tabulating complete positional and dynamical parameters in addition to same orbital solutions with the corresponding orbital plot. We also study the dynamical evolution of the HD 106515 b orbit using, for the first time in this system, an N-body numerical code to simulate and reproduce the longer term octupole perturbations, the so-called Eccentric Kozai-Lidov mechanism (hereafter EKLM).
The Washington Double Star Catalog (Mason et al. Reference Mason, Wycoff, Hartkopf, Douglass and Worley2001), hereafter WDS, centralises all the astrometric measurements for visual double stars, includes a third stellar component (listed as C) with 10.5 V magnitude and low proper motion at an angular separation of 98 arsec to the HD 106515 A. Marmier et al. (Reference Marmier2013) concluded no probable physical relation to the HD 106515 AC system based on the very different proper motions of C and AB. We add a new astrometric measure.
In this work, our main aim is to improve the orbital solution of HD 106515 AB with respect to that determined in Desidera et al. (Reference Desidera2012) by using a method similar to that proposed by Hauser & Marcy (Reference Hauser and Marcy1999). The astrophysical properties estimates performed in this work follow the guidelines detailed in Benavides et al. (Reference Benavides2010) and Rica (Reference Rica2012).
The organisation of this paper is as follows. In Section 2, we present the dynamics of A and C components and the nature of C is confirmed. In Section 3, we detail astrometric dataset used to compute the relative motion of B with respect to A component. In Section 4, we provide new arguments which support that A and B stars are gravitationally bound. The method of orbital calculation is described in Section 5, and the new orbital solutions are exposed in Section 6. Finally, we discuss the results in Section 7 and expose the conclusions in Section 8.
2 ASTROPHYSICAL PROPERTIES OF HD 106515 A AND THE WIDE COMPONENT C
HD 106515 A is a solar metallicity star of V = 7.96 mag classified as a G5V type star (Adams et al. Reference Adams, Joy, Humason and Brayton1935) with a high proper motion. The distance was determined by Hipparcos satellite (reviewed values from van Leeuwen (Reference van Leeuwen2007): π = 28.42 ± 0.96 mas; 35.2 ± 1.2 pc). An E(B − V) = 0.01 was obtained in this work following the procedure described in Benavides et al. (Reference Benavides2010) and Rica (Reference Rica2012). Table 1 lists astrophysical data for the A and B components.
Table 1. Astrophysical data for components of HD 106515 AB.

aValues obtained in this work, converting the Hipparcos magnitudes to V band. The conversion was performed in an iterative process. We compute the spectral type from the initial Hp magnitudes and the parallax, which gives the correction Hp − V for the magnitude. Using these new magnitudes, the process is repeated until the iteration converges into a fix value.
In 1910, Burnham (Reference Burnham1913), using the refractor telescope of 1.0 m in the Yerkes Observatory, observed a star of 9.5 mag (listed in UCAC4 catalogue with V = 10.49 mag) at 99 arcsec and with direction 177° to HD 106515 A. It is listed in the WDS catalogue as the C component, with a small proper motion and therefore it is a background unbound star. Marmier et al. (Reference Marmier2013) already noted the great difference in proper motion and concluded that C component is ‘probably not physical’.
In this work, we confirm the great relative motion between the A and C components. Today, there are 10 astrometric measures in the literature, the last one in 2014, performed by Nuget & Iverson (Reference Nuget and Iverson2015) using the video drift method. By using the historical relative astrometries with a base line of 121 yrs, we show the change of the relative motion of C component with respect to the primary component. These astrometries are listed in the WDS catalogue. We add a new astrometric point for 2010.5589 from WISE catalogue (162.93° and 99.08 arcsec). We obtain a relative motion in RA = +240.3 ± 4.8
![]() $\mathrm{mas \thinspace yr^{-1}}$
and DEC = +43.3 ± 1.1
$\mathrm{mas \thinspace yr^{-1}}$
and DEC = +43.3 ± 1.1
![]() $\mathrm{mas \thinspace yr^{-1}}$
, yielding a proper motion for C (μ(α) = −9.8 ± 4.9
$\mathrm{mas \thinspace yr^{-1}}$
, yielding a proper motion for C (μ(α) = −9.8 ± 4.9
![]() $\mathrm{mas \thinspace yr^{-1}}$
and μ(δ) = −9.6 ± 1.6
$\mathrm{mas \thinspace yr^{-1}}$
and μ(δ) = −9.6 ± 1.6
![]() $\mathrm{mas \thinspace yr^{-1}})$
, which is in agreement with the values present in Tycho-2 catalogue. This clearly confirm that the C component is a background star.
$\mathrm{mas \thinspace yr^{-1}})$
, which is in agreement with the values present in Tycho-2 catalogue. This clearly confirm that the C component is a background star.
By using the reduced proper motion diagram of Jones (Reference Jones1972), photometric data (APASS, 2MASS) and the proper motion (Tycho-2), we suggest an evolved nature for the C component.
We use a CMD (Colour Magnitude Diagram) 2.5 evolutionary isochronesFootnote 1 (we assumed solar metallicity) to determine a spectral type of K0III-IV, which is in excellent agreement with Pickles & Depagne (Reference Pickles and Depagne2010) who also determined a distance of 246 pc by using only photometric data. In addition to the spectral type, we also determine Mv = 2.5+0.5 −0.9 mag and distance of 370+205 −65 pc. The centroid values correspond with solar metallicity and age (metalliticy and age for C component are not listed in the literature). The errors correspond to ages of 2 and 8 Gyr. Therefore, the photometric distance for C is much larger than that corresponding to the AB pair. This is new evidence that reinforces the unbound nature of C with respect to the AB system.
3 ASTROMETRIC DATA AND DYNAMICAL STUDY OF HD 106515 AB
In 1795, de Lalande found a bright star at 8.01 arcsec from HD 106515 with position angle 294.5°. Twenty-eight years later, in 1823, South & Herschel (Reference South and Herschel1824) measured this pair again (288° and 9.23 arcsec). Three years later, Struve (Reference Struve1837) performed a third measure and estimated visual magnitudes of 7.5 and 7.8 for the stellar components. The Struve designation was finally assigned to this double star.
Since its discovery, this pair of stars has been measured 135 times, the last one in 2014 by non-professional astronomers, see Nuget & Iverson (Reference Nuget and Iverson2015), using video drift method. There are many micrometrical measurements but also many other accurate photographic captures. The position angle has decreased from 288° to 266° and the angular separation has changed from 7.9 to 6.9 arcsec. Brian Mason (US Naval Observatory) kindly supplied astrometric information for HD 106515 AB.
The WDS catalogue lists several micrometric measures taken with 0.7-m telescopes (with a Rayleigh resolution limit of 0.19 arcsec)Footnote 2 . Only one high-resolution observation was performed with a telescope of aperture greater than 0.7 m. In 1910, Burnham used the 1.0-m telescope of Yerkes Observatory (with a Rayleigh resolution limit of 0.14 arcsec) in very good sky conditions. HD 106515 A and B have never been observed using digital high-resolution technique (lucky imaging, speckle, or adaptive optics) with a telescope using an aperture greater than 1.0 m.
3.1. Digital high-resolution imaging from TCS/Fastcam
On 2015 March 15 between 01:21 and 02:41 UT, we took about 50 000 short-exposure (30 ms) images of HD 106515 A and B using the FastCam ‘lucky imaging’ camera, that provides a low resolution limit of about 0.14 arcsec. This instrument is mounted in the 1.5-m Carlos Sánchez Telescope in the Observatorio del Teide. More information about the Fastcam camera can be found in Oscoz et al. (Reference Oscoz2008). Our main goal was to detect new close companions to the A and B components. However, no new companion was detected. The FWHM of the final combined images was of about 0.25 arcsec. So, a star as bright as the primary component could be detected at a distance of 0.20 arcsec or wider.
3.2. Dynamical study
We study the relative and projected motions of the secondary component respect to the primary. We perform a weighted fit to analyse the variation of position angle (θ, is the position of the secondary component with respect to the primary measured in degrees from north through east) and angular distance (ρ, the apparent distance between the stellar components measured in arcsecs) over the time (see Figures 1 and 2). The θ values were corrected for precession of the coordinate system. Three measures were rejected due to their large residuals Herschel (Reference Herschel1829, Reference Herschel1870) and the measure from Heidelberg Zodiacal 50 - WFD9999. Therefore, the dynamical study presented here includes 133 positions covering a time baseline of 189 yrs. We applied a weighting procedure to estimate the orbit following prescriptions detailed in Rica et al. (Reference Rica2012). For θ values, the parabolic fit shows smaller RMS (root mean square) residuals than linear fit. However, ρ values show no difference between parabolic and linear fits. The values obtained for
![]() $\text{d}\theta /\text{d}t$
(for mean epoch 2003.22) and
$\text{d}\theta /\text{d}t$
(for mean epoch 2003.22) and
![]() $\text{d}\rho /\text{d}t$
are − 0.133 ± 0.002 deg yr−1 (1.5% of error) and − 5.52 ± 0.14
$\text{d}\rho /\text{d}t$
are − 0.133 ± 0.002 deg yr−1 (1.5% of error) and − 5.52 ± 0.14
![]() $\mathrm{mas \thinspace yr^{-1}}$
(2.5% of error), respectively.
$\mathrm{mas \thinspace yr^{-1}}$
(2.5% of error), respectively.

Figure 1. The weighted linear fit of the position angle (θ) determines a
![]() $\text{d}\theta /\text{d}t = -0.133 \pm 0.002$
deg yr−1. The solid curve is the orbit calculated in this work.
$\text{d}\theta /\text{d}t = -0.133 \pm 0.002$
deg yr−1. The solid curve is the orbit calculated in this work.

Figure 2. The same as Figure 1 but for the distance (ρ). We compute a
![]() $\text{d}\rho /\text{d}t = -5.52 \pm 0.14$
$\text{d}\rho /\text{d}t = -5.52 \pm 0.14$
![]() $\mathrm{mas \thinspace yr^{-1}}$
.
$\mathrm{mas \thinspace yr^{-1}}$
.
Alternately, we compute the projected relative motion following the expression:
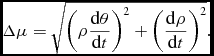 $$\begin{equation}
\Delta \mu = \sqrt{\left(\rho \frac{\text{d}\theta }{\text{d}t}\right)^2 + \left(\frac{\text{d}\rho }{\text{d}t}\right)^2}.
\end{equation}$$
$$\begin{equation}
\Delta \mu = \sqrt{\left(\rho \frac{\text{d}\theta }{\text{d}t}\right)^2 + \left(\frac{\text{d}\rho }{\text{d}t}\right)^2}.
\end{equation}$$
Desidera et al. (Reference Desidera2012) also published similar plots to our Figures 1 and 2 but the weighting procedure and the dynamical parameters they obtained were not detailed. Nevertheless, a comparison of our plots to those presented in Desidera et al. (Reference Desidera2012) shows no significant difference.
We find a Δμ = 16.92 ± 0.27
![]() $\mathrm{mas \thinspace yr^{-1}}$
(for mean epoch 2003.22), which can also be computed by analysing
$\mathrm{mas \thinspace yr^{-1}}$
(for mean epoch 2003.22), which can also be computed by analysing
![]() $\text{d}x/\text{d}t$
and
$\text{d}x/\text{d}t$
and
![]() $\text{d}y/\text{d}t$
. A good way to transform the weights from polar coordinates into weights for Cartesian coordinates was described by van den Bos (Reference van den Bos1932). It was used in this work and follows the expressions:
$\text{d}y/\text{d}t$
. A good way to transform the weights from polar coordinates into weights for Cartesian coordinates was described by van den Bos (Reference van den Bos1932). It was used in this work and follows the expressions:
A parabolic fit for
![]() $\text{d}x/\text{d}t$
shows smaller RMS residuals than that for a linear fit, suggesting the stellar pair follows a curved trajectory. While for
$\text{d}x/\text{d}t$
shows smaller RMS residuals than that for a linear fit, suggesting the stellar pair follows a curved trajectory. While for
![]() $\text{d}y/\text{d}t$
a linear and parabolic fits show the same residuals. The relative motion (for 2003.22) was 17.27 ± 0.18
$\text{d}y/\text{d}t$
a linear and parabolic fits show the same residuals. The relative motion (for 2003.22) was 17.27 ± 0.18
![]() $\mathrm{mas \thinspace yr^{-1}}$
, in agreement with the former value within errors. These results are in good agreement with that presented by Hartkopf & Mason (Reference Hartkopf and Mason2011b), who determined a relative motion of 16.0 ± 1.3
$\mathrm{mas \thinspace yr^{-1}}$
, in agreement with the former value within errors. These results are in good agreement with that presented by Hartkopf & Mason (Reference Hartkopf and Mason2011b), who determined a relative motion of 16.0 ± 1.3
![]() $\mathrm{mas \thinspace yr^{-1}}$
for HD 106515 AB.
$\mathrm{mas \thinspace yr^{-1}}$
for HD 106515 AB.
We also use the individual proper motion from Tycho-2 data to compute the relative motion of B with respect to A. We obtained Δμ = 19.0 ± 1.6
![]() $\mathrm{mas \thinspace yr^{-1}}$
. However, we have to take into account that this method is often less accurate than others using a series of θ and ρ values. Throughout this work, we will use the value of 17.27 ± 0.18
$\mathrm{mas \thinspace yr^{-1}}$
. However, we have to take into account that this method is often less accurate than others using a series of θ and ρ values. Throughout this work, we will use the value of 17.27 ± 0.18
![]() $\mathrm{mas \thinspace yr^{-1}}$
, due to its smaller error.
$\mathrm{mas \thinspace yr^{-1}}$
, due to its smaller error.
We convert the relative projected motion (Δμ in arcsec yr−1) into the relative velocity (
![]() $\mathit {V}_{\mathrm{rel}}$
, in
$\mathit {V}_{\mathrm{rel}}$
, in
![]() $\mathrm{km \thinspace s^{-1}}$
) at the distance (d, in pc) for the system, using the expression:
$\mathrm{km \thinspace s^{-1}}$
) at the distance (d, in pc) for the system, using the expression:
We obtain a relative projected velocity of 2.89 ± 0.10
![]() $\mathrm{km \thinspace s^{-1}}$
. By using the RV, for the stellar components, obtained by Desidera et al. (Reference Desidera, Gratton, Lucatello, Claudi and Dall2006), we calculate a relative RV of − 0.72 ± 0.16
$\mathrm{km \thinspace s^{-1}}$
. By using the RV, for the stellar components, obtained by Desidera et al. (Reference Desidera, Gratton, Lucatello, Claudi and Dall2006), we calculate a relative RV of − 0.72 ± 0.16
![]() $\mathrm{km \thinspace s^{-1}}$
. Thus, the total relative velocity, V
tot, is + 2.97 ± 0.12
$\mathrm{km \thinspace s^{-1}}$
. Thus, the total relative velocity, V
tot, is + 2.97 ± 0.12
![]() $\mathrm{km \thinspace s^{-1}}$
.
$\mathrm{km \thinspace s^{-1}}$
.
4 PROVING THAT HD 106515 AB IS A GRAVITATIONALLY BOUND SYSTEM
We compile solid evidence that HD 106515 AB is a gravitationally bound system. Gould & Chanamé (Reference Gould and Chanamé2004) and Marmier et al. (Reference Marmier2013) concluded that the system is bound based only on the CMP of the components and Gould & Chanamé (Reference Gould and Chanamé2004), assigned the trigonometric parallax of the primary to the secondary component. CMP is necessary but not sufficient evidence to conclude the bound status of a pair of stars. It is possible that two unrelated stars show CMP by chance. Desidera et al. (Reference Desidera2012) performed RV monitoring obtaining very accurate measurements which, added to the CMP, the common RV evidence increases the possibility to be gravitationally bound. From these two pieces of evidence, we can affirm that HD 106515 AB travels with the same space velocity only if A and B components are at the same distance. Therefore, we need to determine if both stars are at the same distance. But even if both stars could be at common distance (within the error margins), it is not possible assure the bound status because the physical separation in line of sight is unknown (and it is possible that the relative velocity is greater than escape velocity).
In the following paragraphs, we show several proofs to demonstrate the bound status of HD 106515 AB. The proofs one and four to six are presented for the first time in this paper.
-
1. Curved motion. The
 $\text{d}x/\text{d}t$
and x − y plots (see Figures 3 and 4) seem to show a small curvature suggesting curved orbital motion. William Hartkopf (United State Naval Observatory) concluded in private communication that, due to the small curvature shown, their linear elements Hartkopf & Mason (Reference Hartkopf and Mason2011b) must be superseded by the dynamical study provided in our paper. The linear fit for
$\text{d}x/\text{d}t$
and x − y plots (see Figures 3 and 4) seem to show a small curvature suggesting curved orbital motion. William Hartkopf (United State Naval Observatory) concluded in private communication that, due to the small curvature shown, their linear elements Hartkopf & Mason (Reference Hartkopf and Mason2011b) must be superseded by the dynamical study provided in our paper. The linear fit for
 $\text{d}x/\text{d}t$
gives an RMS of 0.40 arcsec about 11% higher than the RMS for a non-linear fit. So, relative to this concern, a note has been added to the WDS catalogue:
$\text{d}x/\text{d}t$
gives an RMS of 0.40 arcsec about 11% higher than the RMS for a non-linear fit. So, relative to this concern, a note has been added to the WDS catalogue:
-
A rectilinear solution to AB gives a poor fit, due to slight apparent curvature suggesting very long-period orbital motion.
Our result improves that of previous work Desidera et al. (Reference Desidera2012).
-
-
2. The Tycho-2 catalogue lists a proper motion of μ(α) = −250.1 ± 1.2
 $\mathrm{mas \thinspace yr^{-1}}$
and μ(δ) = −52.9 ± 1.2
$\mathrm{mas \thinspace yr^{-1}}$
and μ(δ) = −52.9 ± 1.2
 $\mathrm{mas \thinspace yr^{-1}}$
for the primary star and μ(α) = −240.8 ± 1.0
$\mathrm{mas \thinspace yr^{-1}}$
for the primary star and μ(α) = −240.8 ± 1.0
 $\mathrm{mas \thinspace yr^{-1}}$
and μ(δ) = −69.4 ± 1.0
$\mathrm{mas \thinspace yr^{-1}}$
and μ(δ) = −69.4 ± 1.0
 $\mathrm{mas \thinspace yr^{-1}}$
for the secondary star. Both components have a high CPM as pointed out Gould & Chanamé (Reference Gould and Chanamé2004) and Marmier et al. (Reference Marmier2013).
$\mathrm{mas \thinspace yr^{-1}}$
for the secondary star. Both components have a high CPM as pointed out Gould & Chanamé (Reference Gould and Chanamé2004) and Marmier et al. (Reference Marmier2013). -
3. Duflot, Figon, & Meyssonnier (Reference Duflot, Figon and Meyssonnier1995) obtained radial velocities of +21.6 and +18.1
 $\mathrm{km \thinspace s^{-1}}$
for the primary and secondary components, respectively, which are based on 27 individual measurements with a standard deviation of 1.78
$\mathrm{km \thinspace s^{-1}}$
for the primary and secondary components, respectively, which are based on 27 individual measurements with a standard deviation of 1.78
 $\mathrm{km \thinspace s^{-1}}$
. More accurate RV determinations were performed by Desidera et al. (Reference Desidera, Gratton, Lucatello, Claudi and Dall2006) who obtained values of radial velocities for the A and B components of + 20.66 ± 0.11 and + 19.94 ± 0.11
$\mathrm{km \thinspace s^{-1}}$
. More accurate RV determinations were performed by Desidera et al. (Reference Desidera, Gratton, Lucatello, Claudi and Dall2006) who obtained values of radial velocities for the A and B components of + 20.66 ± 0.11 and + 19.94 ± 0.11
 $\mathrm{km \thinspace s^{-1}}$
, respectively, on 2003 March 21. So, both components have a very similar RV.
$\mathrm{km \thinspace s^{-1}}$
, respectively, on 2003 March 21. So, both components have a very similar RV. -
4. The secondary component is classified as a G8V (Adams et al. Reference Adams, Joy, Humason and Brayton1935) type star with V = 8.2. Houk & Swift (Reference Houk and Swift1999) classified it as a subgiant K0/1 IV. We use an evolutionary isochrone (solar age and metallicity is assumed), accessing to a CMD 2.5 interface. Main sequence is assumed for the secondary and in the isochrone, we use Hipparcos/Tycho-2 data. If the secondary component is on the main sequence then both stars are on the same isochrone and therefore both stars present common distances. However, we can consider that there is still a remote possibility that HD 106515 B is a distant giant star with CPM and RV. However, Desidera et al. (Reference Desidera, Gratton, Lucatello, Claudi and Dall2006) determined log(g) of 4.31 and 4.32 for the primary and secondary components, respectively, which are typical values of stars on the main sequence and with colours as those listed in the Tycho-2 catalogue. Therefore, the secondary member is, as assumed, a main sequence star, and so at the same distance that the primary star.
-
5. Celestial mechanics is commonly used to estimate the escape velocity of stellar system (Close, Richer, & Crabtree Reference Close, Richer and Crabtree1990; Mamajek Reference Mamajek2013) and compare it to the observed total relative velocity of star B with respect to the A. A detailed description on the escape velocity computation can be found in Rica (Reference Rica2011). Given the separation between A and B components, the r parameter is unknown, so we use its projection over the plane of the sky,
 $242.5 \pm 9.2 \thinspace \mathrm{AU}$
. It is not possible to calculate the true value of V
esc, but only its upper limit, V
esc-max. Thus, we obtain V
esc-max = 3.62 ± 0.08
$242.5 \pm 9.2 \thinspace \mathrm{AU}$
. It is not possible to calculate the true value of V
esc, but only its upper limit, V
esc-max. Thus, we obtain V
esc-max = 3.62 ± 0.08
 $\mathrm{km \thinspace s^{-1}}$
. A Monte Carlo approach gives 100% simulations where
$\mathrm{km \thinspace s^{-1}}$
. A Monte Carlo approach gives 100% simulations where
 $V_{\text{tot}} < V_{\mathrm{esc-max}}$
so, from this point of view, V
tot (calculated in Section 3) is smaller than V
esc-max and HD 106515 AB could be a gravitationally bound binary.
$V_{\text{tot}} < V_{\mathrm{esc-max}}$
so, from this point of view, V
tot (calculated in Section 3) is smaller than V
esc-max and HD 106515 AB could be a gravitationally bound binary.Could HD 106515 AB be involved in a dissolution process? During the lifetime of a wide binary, the numerous encounters with passing stars and giant molecular clouds are the most important sources of disruption (Weinberg, Shapiro, & Wasserman Reference Weinberg, Shapiro and Wasserman1987; Jiang & Tremaine Reference Jiang and Tremaine2010). The Galactic tidal forces only affect very wide binaries with separations of several tens of thousands of AU. HD 106515 AB has a projected separation of 0.0012 pc. According to Figure 6 of Weinberg et al. (Reference Weinberg, Shapiro and Wasserman1987), wide binaries with an initial semimajor axis a0 = 2000 AU (0.010 pc), with a total mass of 1 M⊙ and an age of
 $6-8 \thinspace$
Gyr (comparable to the age of HD 106515 A) have a survival probability of 90–95%. In fact, HD 106515 AB has a physical projected separation about eight times smaller and a total mass nearly two times larger. This yields a binding gravitational energy about 26 times larger and a survival probability of nearly 100%, which means HD 106515 AB is insensitive to external perturbers. Therefore, in this frame, three possible scenarios can be described:
$6-8 \thinspace$
Gyr (comparable to the age of HD 106515 A) have a survival probability of 90–95%. In fact, HD 106515 AB has a physical projected separation about eight times smaller and a total mass nearly two times larger. This yields a binding gravitational energy about 26 times larger and a survival probability of nearly 100%, which means HD 106515 AB is insensitive to external perturbers. Therefore, in this frame, three possible scenarios can be described:
-
– If the stellar components were born gravitationally bound, the system will remain bound today because it is insensitive to external perturbers.
-
– In case the stellar components were born unbound and became bound later, the same conclusion as in the first scenario can be assumed.
-
– A third scenario would imply that the stellar components are unbound during all their lifetime. This situation was ruled out in this work because the secondary star would not spend much time close to HD 106515 A. In fact, considering a V tot = +2.97 ± 0.12
 $\mathrm{km \thinspace s^{-1}}$
, the B component would spend only 0.6 Myr within the tidal radius (1.6 pc) of the primary star. We calculate the tidal radius of the primary star using formula (2) in Mamajek et al. (Reference Mamajek2013).
$\mathrm{km \thinspace s^{-1}}$
, the B component would spend only 0.6 Myr within the tidal radius (1.6 pc) of the primary star. We calculate the tidal radius of the primary star using formula (2) in Mamajek et al. (Reference Mamajek2013).
-
-
6. The statistical criterion. Grocheva & Kiselev (Reference Grocheva and Kiselev1998) proposed using the real distribution of proper motions to determine the possible physical relation of a pair of stars. The probability (Prob) that a pair of stars with proper motions between that of the primary and secondary is defined as S/N, where S is the number of stars with similar proper motions in a determined sky area, and N is the total number of stars in the same area. Physical pairs were defined for
 $\text{Prob} < 0.01$
. We use the PPMXL catalogue in order to obtain
$\text{Prob} < 0.01$
. We use the PPMXL catalogue in order to obtain
 $\text{Prob}$
using a circular area with a radius of 2°. The total number of stars (N) is 80 580. Only three stars with similar proper motion was found (and two are the stellar component of HD 106515) yielding
$\text{Prob}$
using a circular area with a radius of 2°. The total number of stars (N) is 80 580. Only three stars with similar proper motion was found (and two are the stellar component of HD 106515) yielding
 $\text{Prob} = 3.7$
×
$\text{Prob} = 3.7$
×
 $\thinspace 10^{-5}$
, suggesting again physical relation.
$\thinspace 10^{-5}$
, suggesting again physical relation.

Figure 3. Orbit of HD 106515 AB presented in this work. The line of sight separations, z, of A and B is of − 5.3 AU at the epoch 2003.22. The astrometric measures are plotted as crosses, circles, and squares. The filled circle in the (0,0) coordinate corresponds with the position of the primary stellar component.
5 ANALYSIS OF THE ORBITAL MOTION
Since HD 106515 AB is composed of a pair of gravitationally bound stars, it is also important to obtain for this system the orbital parameters and the distribution of possible orbital solutions.
5.1 Constraining the semimajor axis
We can constrain the value of the semimajor axis (a arcsec) by using a relationship between ρ and a arcsec. Burningham et al. (Reference Burningham2009) used the method proposed by Torres (Reference Torres1999) to obtain a relation between the physical projected separation (s) and semimajor axis (a), both in AU. They assumed randomly distributed viewing angles (inclinations) and a uniform distribution of eccentricities ranging 0 < e < 1 in order to derive a relationship of
For HD 106515 AB, the value for a (AU) is 267+221 −87 AU. The error interval is defined as a 68% confidence level. The work of Torres (Reference Torres1999) studies the distribution of a arcsec/ρ Footnote 3 and proposes a lower limit of 0.5ρ in the semimajor axes estimation. This lower limit occurs when the binary is at apastron configuration and the orbit presents an eccentricity very close to 1. A confidence level of 90–95% (0.5ρ, 3.0ρ) for the semimajor axis is also found in Torres (Reference Torres1999).
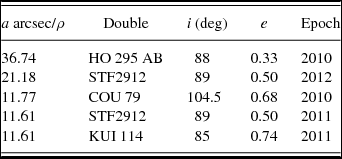
In this work, we present an independent empirical study of the relation between ρ and a arcsec, analysing about 300 high-quality orbits (grade 1 and 2) extracted from the Sixth Catalog of Orbits of Visual Binary Stars Hartkopf & Mason (Reference Hartkopf and Mason2011a). For each binary, the separations corresponding to the epochs 2008–2012 were compared with the semimajor axes of the orbit. Although the most extreme a arcsec/ρ value was 36.74 (for HO 295 AB) only 1–2% of the binaries show a arcsec/ρ > 10. The highest a arcsec/ρ values occur in very inclined orbits, where close encounters are favoured in or near the apparent periastron (see Table 2). Other possibilities for upper limits in a arcsec/ρ could be very eccentric orbits with the secondary star in the apparent periastron point. Only a 1.6% of the all orbital binaries compiled shows eccentricities higher than 0.95 (0.2% presents e > 0.99). For HD 106515 AB system, we obtain s = 242.5 ± 9.2 AU (in 2003.22). The values of semimajor axis a can then be constrained to (121–2425) AU with a 98–99% confidence level (0.5–10s).
Table 2. Highest values of a arcsec/ρ.
5.2 Method of orbital calculation
An orbit of a binary star is defined with seven parameters: period (P), time of periastron passage (T), eccentricity (e), semimajor axis (a (arcsec)), inclination (i), argument of periastron (ω), and node (Ω). To obtain the orbital solutions, we have used a method based on that presented by Hauser & Marcy (Reference Hauser and Marcy1999). Desidera et al. (Reference Desidera2012) used the same method to determine the distribution of the orbital solutions for HD 106515 AB. Therefore, given the simultaneity of position and velocity vectors, we can apply Newtonian mechanics to determine the distribution of the orbital parameters.
The velocity vector is composed of Vx and Vy perpendicular components in the plane of the sky that are computed from the astrometric data. The velocity in the line of sight, Vz , arises from the differential RV of the stellar members for the system. On the other hand, the position vector is made up by the x and y coordinates (on the plane of the sky) which are calculated from the astrometric data as well, and z, the component in the line of sight.
The z parameter can be constrained following the procedure proposed by Hauser & Marcy (Reference Hauser and Marcy1999) for bound systems. Further constraint on z is possible if the observed orbital arc shows a curvature. In such cases, the radius of the curvature (ρc), can be obtained following the procedure used in the AMP method. HD 106515 AB shows a very small orbital curvature that allows an estimated value for ρc. Our result yields an r value very close to s and therefore the orbit of HD 106515 AB is compatible with low inclination.
The Keplerian orbital family, defined by the range of z values, was further constrained using the limits of semimajor axis values, as described in Section 5.1. The initial weights for the astrometric measures were consistently assigned following the same procedure used in the linear fit.
6 THE ORBIT OF HD 106515 AB
The orbital parameters of HD 106515 B relative to the A component were determined taking into account their masses (see Table 1), the relative position (x, y, z) and velocity vectors (Vx , Vy , Vz ) that ensure a bound orbit.
Table 3 shows a summary of the astrometric, dynamical, and velocity data considered in the orbital calculation for 2003.22 epochFootnote 4 .
Table 3. Astrometric, dynamical, and velocity data for HD 106515 AB.

The range of z-values that fulfill a bound condition is − 285 ⩽ z ⩽ +285 AU. However, if we consider the limits to the semimajor axis (see Section 5.1), the new range of z is − 249 ⩽ z ⩽ +249 AU. So, according to this interval, in Table 4, we list the orbital parameters for five values of z ( − 231, − 117, 0, +117, +231 AU) which correspond to radius vector of r = s, 1.11s (the median ratio of r and s) and 1.38s (75% percentile)Footnote 5 , respectively. Table 4 also lists the periastron distance (q).
Table 4. Computed orbital parameters of HD 106515 AB, assuming r = s (z = 0), r = 1.11s (z = ±117), and r = 1.38s (z = ±231).
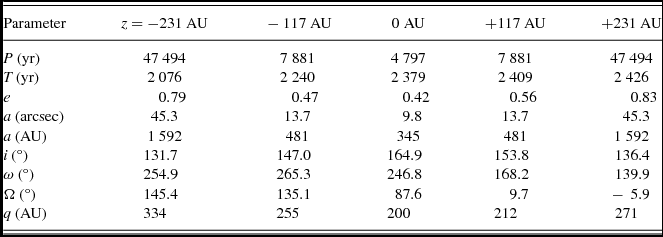
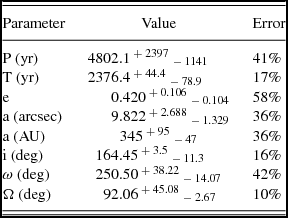
We obtain a family of orbits for 1 000 of different values for z distributed in the range of possible values. From these orbits, we choose those showing the smallest χ2 residuals. Table 5 compiles the orbital solution obtained. The errors were determined following the procedure of Kiselev et al. (Reference Kiselev, Kiyaeva, Romanenko and Gorynya2012), page 532. In short, the uncertainties are computed as function only of the errors in the initial data. The last column in Table 5 shows the error due to the parallax uncertainty. Figures 3 and 4 show the final orbital solution obtained for HD 106515 AB, which yields a value of z = −5.3 AU at 2003.22 epoch, in agreement with ρ c value.
Table 5. Orbital parameters for HD 106515 AB binary.
Because the binary shows a small arc, the orbital solution present here is preliminary, and so we estimate the distribution of each orbital parameter as function of z (see Figure 5). A visual comparison of these distributions with the corresponding plots presented in Desidera et al. (Reference Desidera2012) shows no significant difference. However, our distribution of the eccentricities gives slightly higher values in respect to that work. A different weighting process in Desidera et al. (Reference Desidera2012) could show slighly different values for
![]() $\text{d}\theta /\text{d}t$
and
$\text{d}\theta /\text{d}t$
and
![]() $\text{d}\rho /\text{d}t$
. Unfortunately, no information about this was detailed in Desidera et al. (Reference Desidera2012). For example, graphically from his Figure 4, we obtained a value for
$\text{d}\rho /\text{d}t$
. Unfortunately, no information about this was detailed in Desidera et al. (Reference Desidera2012). For example, graphically from his Figure 4, we obtained a value for
![]() $\text{d}\theta /\text{d}t$
of − 0.118
$\text{d}\theta /\text{d}t$
of − 0.118
![]() $\mathrm{deg \thinspace yr^{-1}}$
, slighly smaller than our value. If we use this smaller value in our calculations, then the eccentricity vs. z is in very good agreement with the work of Desidera et al. (Reference Desidera2012).
$\mathrm{deg \thinspace yr^{-1}}$
, slighly smaller than our value. If we use this smaller value in our calculations, then the eccentricity vs. z is in very good agreement with the work of Desidera et al. (Reference Desidera2012).

Figure 5. Distribution of orbital parameters vs. z.
7 THE CIRCUMPRIMARY PLANETARY ORBIT
We have showed that HD 106515 AB is a gravitationally bound system. The dynamical study here presented uses several tests (some of them used for the first time for this system), which point out the gravitationally bound status. In this section, we will discuss how this scenario influences the planetary orbit around HD 106515A. The planet was spectroscopically monitored by Mayor et al. (Reference Mayor2011) since 1998 using the CORALIE spectrograph, located at the 1.2-m EULER Swiss telescope at La Silla Observatory and over about 11 yrs using the spectrograph SARG at TNG Desidera et al. (Reference Desidera2012).
Desidera et al. (Reference Desidera2012) also computed the critical semimajor axis [calculated following Holman & Wiegert (Reference Holman and Wiegert1999) prescriptions] and concluded that the planetary orbit is stable in a long term, possibly affected by periodic modulation due to KL (
![]() $P_{\text{KL}}$
). The formula for the critical semimajor axis in Holman & Wiegert (Reference Holman and Wiegert1999) only uses the outer binary eccentricity but not the planetary eccentricity, which is high for HD 106515 b, and does not include any effect due to the mutual inclination.
$P_{\text{KL}}$
). The formula for the critical semimajor axis in Holman & Wiegert (Reference Holman and Wiegert1999) only uses the outer binary eccentricity but not the planetary eccentricity, which is high for HD 106515 b, and does not include any effect due to the mutual inclination.
Marmier et al. (Reference Marmier2013) concluded that the KL, with a timescale of 3.3 Myr, is not suppressed by the much longer general relativistic timescale of 1.1 Gyr. To confirm this result, in this work, we have plotted the possible values of
![]() $P_{\text{KL}}$
as a function of the outer semimajor axis and eccentricity obtained from a sample of about 27 500 orbits. This was performed using all the input parameters used in the orbital calculation procedure within 95% (2σ) interval confidence. Figure 6 was built for a planetary orbit inclination of 90° (edge-on orbit), that is, for a planetary mass of 9.6 Jupiter masses.
$P_{\text{KL}}$
as a function of the outer semimajor axis and eccentricity obtained from a sample of about 27 500 orbits. This was performed using all the input parameters used in the orbital calculation procedure within 95% (2σ) interval confidence. Figure 6 was built for a planetary orbit inclination of 90° (edge-on orbit), that is, for a planetary mass of 9.6 Jupiter masses.
![]() $P_{\text{KL}}$
ranges from several millions years for small semimajor axis (a < 400 AU) to about 0.2–0.3 Gyr for orbits with very high semimajor axis and eccentricities. The only scenario where
$P_{\text{KL}}$
ranges from several millions years for small semimajor axis (a < 400 AU) to about 0.2–0.3 Gyr for orbits with very high semimajor axis and eccentricities. The only scenario where
![]() $P_{\text{KL}}$
could be suppressed by general relativistic precession period happens when the planet is in a nearly face-on orbit. Figure 7 plots
$P_{\text{KL}}$
could be suppressed by general relativistic precession period happens when the planet is in a nearly face-on orbit. Figure 7 plots
![]() $P_{\text{KL}}$
for a planetary inclination of 0.2° (when the mass of the ‘planet’ is of 2.6
$P_{\text{KL}}$
for a planetary inclination of 0.2° (when the mass of the ‘planet’ is of 2.6
![]() $\text{M}_{\odot }$
) with values for
$\text{M}_{\odot }$
) with values for
![]() $P_{\text{KL}} = 1.2$
Gyr and very high semimajor axis and eccentricities. But this scenario is highly unlikely.
$P_{\text{KL}} = 1.2$
Gyr and very high semimajor axis and eccentricities. But this scenario is highly unlikely.

Figure 6. Kozai–Lidov periodic modulation for an edge-on planetary orbit (inclination = 90° and a planetary mass of 9.6 Jupiter mass). Colour figure included in the electronic paper.

Figure 7. Kozai–Lidov periodic modulation for a nearly face-on planetary orbit (inclination = 0.2° and a ‘planetary’ mass of 2.6
![]() $\text{M}_{\odot }$
). Colour figure included in the electronic paper.
$\text{M}_{\odot }$
). Colour figure included in the electronic paper.
To activate the KL, the relative inclinations of planetary and binary orbital planes (ΔI) must be of 39.2° Kozai (Reference Kozai1962). But the angle needed to produce the eccentricity of HD 106515 b, which is 0.57, could be calculated approximately from the formula that relates the maximum eccentricity and the mutual inclination (Kozai (Reference Kozai1962) and Lidov (Reference Lidov1962)), from which we derive
The standard Kozai–Lidov mechanism (hereafter SKLM) has two major assumptions: (1) one of the component of the inner binary (in this case the planet) has negligible mass and therefore zero angular momentum; and (2) the outer orbit (that is HD 106515 AB) is circular. HD 106515b is a very massive planet, nearly 10 Jupiter mass, so its angular momentum is 0.60
![]() $\text{M}_{\odot } ^{1/2} \thinspace UA^{7/2} \thinspace \text{yr}^{-2}$
. However, this is only about 0.01% of the total angular momentumFootnote
6
and hence the first assumption may be considered valid.
$\text{M}_{\odot } ^{1/2} \thinspace UA^{7/2} \thinspace \text{yr}^{-2}$
. However, this is only about 0.01% of the total angular momentumFootnote
6
and hence the first assumption may be considered valid.
The orbit of HD 106515 AB is eccentric (e ⩾ 0.42) and therefore the second assumption is not fulfilled. Naoz et al. (Reference Naoz, Farr, Lithwick, Rasio and Teyssandier2011) and Naoz, Farr, & Rasio (Reference Naoz, Farr and Rasio2012) showed that this situation leads to longer term octupole perturbations on the inner orbit (the so-called Eccentric Kozai–Lidov Mechanism, EKLM). The EKLM can lead to a dynamical behaviour significantly different from the SKLM. So, the inner orbit can flip between prograde and retrograde and in addition can reach extremely high values in eccentricity.
We use the REBOUND N-body numerical code (Rein & Liu Reference Rein and Liu2012) to perform numerical simulations. This code employs the high-order IAS15 integrator (Integrator and Adaptive Step-size control) based on a 15th-order Gauβ-Radau quadrature (Rein & Spiegel Reference Rein and Spiegel2015). We performed several simulations varying the initial mutual inclination (ΔI) with the time. Since the angular momentum of the planet is negligible with respect to the total angular momentum, the variation of the planetary inclination causes most of the variation of ΔI.
The input orbital parameters for the simulations were
-
• for the outer orbit, that is, for the binary star, we consider those listed in the Table 5 in addition to the stellar masses of the Desidera et al. (Reference Desidera2012) listed in Table 1.
-
• for the planetary orbit, we use the orbital parameters listed in The Extrasolar Planets Encyclopaedia webFootnote 7 except for i and Ω, values that change in each simulations (see Table 6 describe in the next parragraph).
Table 6. The periodical modulation of the planetary eccentricity and inclination.

Figure 8 shows the evolution of the planetary orbit’s eccentricity and inclination for different inclinations of the planet of 130°, 100°, and 74°. These different inclinations yields to different initial mutual inclinatons of ΔI of 51.2°, 68.7° and 84.6°. The results of these simulations (in addition to other simulation for ΔI = 43.0 or planetary inclination of 140°) are detailed in Table 6 which lists ΔI, the planetary orbit’s inclination (io
), the longitude of the ascending node (Ω
o
), the periodic modulation of the eccentricity (
![]() $P_{\text{ecc}}$
) and its lower-upper limits, and the periodic modulation of the inclination (
$P_{\text{ecc}}$
) and its lower-upper limits, and the periodic modulation of the inclination (
![]() $P_{\text{inc}}$
) and its lower–upper limits. The periodic modulation is expressed in millions of years and the periodic oscillations for the inclination is exactly twice greater than for the eccentricity. For ΔI = 84.6°, the inclination flips from prograde to retrograde ranges from 80° to 144°. We also ran a simulation for ΔI = 89.6°. At 0.78 million yrs, the planetary eccentricity increased to 0.9997 that yields a periastron distance of 0.00135772 AU or 203 658 km. That is, HD 106515 b collided with HD 106515 A.
$P_{\text{inc}}$
) and its lower–upper limits. The periodic modulation is expressed in millions of years and the periodic oscillations for the inclination is exactly twice greater than for the eccentricity. For ΔI = 84.6°, the inclination flips from prograde to retrograde ranges from 80° to 144°. We also ran a simulation for ΔI = 89.6°. At 0.78 million yrs, the planetary eccentricity increased to 0.9997 that yields a periastron distance of 0.00135772 AU or 203 658 km. That is, HD 106515 b collided with HD 106515 A.

Figure 8. Evolution of the planetary orbit’s eccentricity and inclination using REBOUND N-body numerical code. Simulations are showed for mutual inclination (ΔI) of 51.2°, 68.7°, and 84.6° with maximum eccentricity of 0.79, 0.90, and 0.995 and periodic oscillation of 1.3, 1.05, 1.13 million yrs (oscillation are two times larger than the inclination). For ΔI = 84.6°, the inclination flips from prograde to retrograde.
Summarising the planetary orbit is stable in the long term but modulated by periodic pertubations of about 2–3 millions yrs due to EKLM.
8 CONCLUSIONS
We conducted a multi-purpose study on the stellar system HD 106515 AB. Using publicly available astrometric data, velocity and Hipparcos trigonometric parallax, we developed a dynamical study of this binary system.
We considered 133 measures reported in the WDS catalogue describing an orbital arc of about 21° in a time base of 189 yrs. From this observational arc and using several tests (same of them used for the first time), we demonstrated that HD 106515 AB is a bound system. We computed the orbital parameters of this binary for the first time. Considering the instantaneous relative position and velocity, we estimated the most probable orbital solution with an orbital period of about 4 800 yrs, a semimajor axis of ~ 350 AU, an inclination of ~ 165° and an eccentricity about 0.42.
We also found evidence of the influence of the binary orbit on the planetary one present in the HD 106515 A star. The critical semimajor axis ensures the stability of the planetary orbit. The ratio between Kozai and general relativistic precession periods ( ≪ 1) suggests that the Kozai mechanism could be perturbing the planetary orbit.
Our study of the dynamical evolution of the planetary orbit using REBOUND N-body numerical code shows periodic oscillation for the eccentricity larger than those calculated using the classical formula. This effect is greater for low ΔI. The reason being neither the octopole and higher moments, nor the eccentricity of the HD 106515 AB are taken into account for this formula. For example, considering the ΔI values listed in Table 6, the maximum eccentricities calculated are 0.33, 0.59, 0.88, and 0.993. For the last two values of ΔI, our maximum eccentricities are very close.
We determined that ΔI must be greater than 50.5°, which yields a planetary eccentricity of 0.57. On the other hand, the REBOUND simulations show that higher ΔI leads to more eccentric orbits.
Marmier et al. (Reference Marmier2013) estimated a P KL of 3.3 Myr assuming an outer eccentricity with a median value of a distribution f(e) = 2e. Our eccentricity periodical modulation is smaller than that value.
In addition to all above exposed, the work here presented try to be an example of how using publicly available data and high precission measurements, dynamical studies of long-period binary system with exoplanets can be performed in the pre-GAIA era.
ACKNOWLEDGEMENTS
Rafael Barrena acknowledges financial support from the Spanish Ministry of Economy and Competitiveness (MINECO) under the 2011 Severo Ochoa Program MINECO SEV-2011-0187.
This research work makes use of data from the Two Micron All Sky Survey (2MASS), which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. The study here presented also uses the Washington Double Star Catalog, maintained at the U.S. Naval Observatory and the SIMBAD astronomical database and VizieR astronomical catalogues service, both maintained and operated by the Center de Données Astronomiques de Strasbourg (http://cdsweb.u-strasbg.fr/).
The authors thank Josefina Ling, Henry Zirm, and Frank Smith for their respective reviews of this work.


















