The inverse relationship between food price and energy density: is it spurious?

Abstract

Objective

An important debate in the literature is whether or not higher energy-dense foods are cheaper than less energy-dense foods. The present communication develops and applies an easy statistical test to determine if the relationship between food price and energy density is an artifact of how the data units are constructed (i.e. is it ‘spurious’ or ‘real’?).

Design

After matching data on 4430 different foods from the National Health and Nutrition Examination Survey with corresponding prices from the Center for Nutrition Policy and Promotion’s Food Prices Database, we use a simple regression model to test if the relationship between food price and energy density is ‘real’ or ‘spurious’.

Setting

USA.

Subjects

Total sample size is 4430 observations of consumed foods from 4578 participants from the non-institutionalized US adult population (aged 19 years and over).

Results

Over all 4430 foods, the null hypothesis of a spurious inverse relationship between food price per energy density and energy density is not rejected. When the analysis is broken down by twenty-five food groups, there are only two cases where the inverse relationship is not spurious. In fact, the majority of non-spurious relationships between food price and energy density are positive, not negative.

Conclusions

One of the main arguments put forth regarding the poor diet quality of low-income households is that high energy-dense food is cheaper than lower energy-dense food. We find almost no statistical support for higher energy-dense food being cheaper than low energy-dense food. While economics certainly plays a role in explaining low nutritional quality, more sophisticated economic arguments are required and discussed.

The diets of most Americans do not meet dietary recommendations^{( 1 )}. The cost of food has become a simple explanation because there is a common (mis?)perception that healthy foods cost more than less healthy foods^{( 2 )}. This perception is based on research that is under debate in the literature.

The debate began with researchers collecting data on the prices p of many different foods, expressed in price per gram, and the kilocalories k (1 kcal=4·184 kJ) per gram associated with those foods. The price was then expressed as price per kilocalorie which, because energy density d is defined as kilocalories ÷ grams, is equivalent to price per gram per energy density or r ( $=p/d$ ). Through summary statistics, plots and regression analyses these researchers then claimed there was a ‘real’ inverse relationship between the price of food and energy density^{( 3 – 9 )}.

Not long after this initial research emerged, others began to question these results^{( 2 , 10 – 13 )}. These other researchers argued that the inverse relationship between the price of food and energy density was a mathematical artifact created by the way the food price was constructed and therefore was a ‘spurious’ relationship. The ‘spurious’ argument is based on the fact that if the price of food is defined as price per energy density, then energy density appears in both variables but on opposite sides of the divisor (i.e. p/d and d), so one would expect the variables to be inversely related. The ‘spurious’ proponents have taken several approaches to demonstrate their argument. For example, Burns et al.^{( 11 )} collected energy content data on 212 foods in Melbourne, Australia and generated random numbers for the price of each food. Then, using the data transformation employed by the ‘real’ proponents, they plotted the data showing a negative relationship very comparable to that shown by the ‘real’ proponents. Conclusion: even if the underlying relationship between food price and energy content is completely random, the data transformation will create a figure implying a negative relationship. Similarly, Lipsky^{( 12 )} generated three variables randomly, representing ‘kilocalories’, ‘grams’ and ‘total price’, applied the data transformation used by the ‘real’ proponents, and generated figures like those shown by Burns et al.^{( 11 )} and the ‘real’ proponents. Again, the conclusion is that the relationship between food price and energy density, as measured by the ‘real’ proponents, is spurious. Carlson and Frazao^{( 2 )} were not so much interested in generating a negative relationship from random data but simply demonstrated that how one ranks foods as expensive or cheap will depend on how price is measured. For example, they find that ‘healthy’ foods are more expensive than ‘less healthy’ foods only if one uses a price per kilocalorie measure, as used by the ‘real’ proponents, but if either a price per edible grams or a price per average portion is used then healthy foods are cheaper than less healthy foods. Conclusion: units matter. While these empirical examples are certainly suggestive and compelling, technically they do not constitute a formal proof, in the mathematical sense (i.e. a relationship that holds for all values of the variables). Lipsky et al.^{( 13 )} show that if one is willing to make some distributional assumptions about the variables involved in the analysis, then the conditional expectation of the price per energy density will always be inversely related to energy density.

Obviously settling this debate is very important because the implications for policy are dramatic. If the inverse relationship between food price and energy density is ‘real’ then the higher obesity rates in low-income groups has a simple economic story: low-income groups eat more high energy-dense foods because these foods are cheaper, so addressing income inequality should significantly ease the problem^{( 3 – 9 )}. Alternatively, if the inverse relationship is ‘spurious’, the economic story relating lower income to higher obesity rates must be more sophisticated and requires more work.

Although the analyses of the ‘spurious’ proponents are conceptually, visually, empirically and in a limited mathematical sense compelling, their analyses fall short of being a formal measure and test of spurious correlation. Indeed, in his response to the comment by Lipsky et al.^{( 13 )}, Drewnowski^{( 14 )} states (p. 868), ‘These are not scientific comments regarding data analysis, interpretations, or conclusions…these are value judgments.’ One would hope a formal statistical test would help settle this debate because statistical tests are perhaps the main instrument utilized in science for analysing data and drawing conclusions. The lack of a formal test in this debate is very surprising, as there is a long history in the statistics literature on this issue under the more common heading of ‘ratio analysis and spurious correlation’^{( 15 – 21 )} and none of this literature has been utilized in the debate. As shown below, it turns out that the relationship between price and energy density is not simply either ‘real’ or ‘spurious’ for all data but will depend on the data and hence, as consistent with all statistical-type analyses, requires a test. The goal of the present communication is to develop and demonstrate a simple test that does not require simulated data and can be applied to any data set. This goal is achieved by using some basic mathematics that leads to a one-sided t test of spurious correlation in a simple regression. Whereas previous studies have considered rather small sample sizes (e.g. 300 foods or less), here the test is applied to 4430 different foods.

Methods

As indicated, there currently has been no formal test, so the test procedure must first be explained before turning to the application. The testing method will be applicable to any price/energy density data set.

Analytical representation

Pearson^{( 15 )}, a key figure in the development of statistics, wrote of the spurious correlation problem of ratios in 1897. He described the general situation where there are three component variables used to construct other (ratio) variables. In the present setting, let p be price of food per gram and d be energy density. The ratio variable, $r=p/d$ , is then price of food per gram divided by energy density. Pearson^{( 15 )} showed that even if there is no correlation between component variables, such as p and d, there still may be correlation between the constructed variables r and d and he defined this to be ‘spurious’ correlation. Following the literature^{( 15 – 21 )}, this is the definition used here as well. Although straightforward, Pearson’s approach relies on a first-order approximation that may give misleading results^{( 21 )}. While inspired by Pearson and others^{( 15 – 21 )}, our approach is novel and does not require any approximation.

Assume that the possible relationship between the component variables p and d is represented in function notation as: $p={\mathop{\rm f}\nolimits} (d)$ . The ‘real’ proponents focus on the relationship between the price per gram divided by energy density $r=p/d$ and energy density d ^{( 3 – 9 )}. Substituting for p then gives: $r={\mathop{\rm f}\nolimits} (d)/d$ . The question is: what is the relationship between r and d? Note that even if there is no relationship between p and d (i.e. p remains constant as d changes), r will still decrease as d increases because the denominator of r will increase. However, more generally, using the quotient rule of calculus, it can be shown that r could be negatively, positively or not related to d. We utilize some basic mathematics to formalize this idea and develop the test.

As the analysis is working with ratios, log functions and operators are convenient; indeed the graphs in this literature are often reported on a log scale. Let the relationship $p={\mathop{\rm f}\nolimits} (d)$ be represented by the double logarithm regression model: $\ln p=\alpha {\plus}\beta \ln d{\plus}{\varepsilon}$ , where ‘ln’ is the natural logarithm operator, α is the unknown intercept, β is the unknown slope and ε is the disturbance term. If there is no relationship between $\ln p$ and $\ln d$ , then $\beta =0$ .

Now by definition, the price per gram divided by energy density is $r=p/d$ , so by the rules of logarithms: $\ln r=\ln (p/d)=\ln p{\minus}\ln d$ . Note the subtraction of $\ln d$ in the logarithmic form is due to the fact that energy density d is in the denominator of the price definition. Direct substitution for $\ln p$ yields:

$$\eqalignno{ \ln r=\alpha {\plus}(\beta {\minus}1)\ln d{\plus}{\varepsilon} \cr =\alpha {\plus}\lambda \ln d{\plus}{\varepsilon}, $$

where the second line just recognizes in a regression framework that only the slope $(\beta {\minus}1)$ can be estimated, so this slope coefficient is defined as $\lambda =(\beta {\minus}1)$ . So when a regression model like equation (1) is estimated, an estimate of the intercept α and an estimate of the slope λ will be obtained. The estimate of the slope λ, along with its t statistic or P value, will be used to draw inferences about whether the relationship between price and energy density is negative and significant. However, note that the value of λ (negative, zero or positive) is actually determined by the value of β relative to ${\minus}1$ .

A spurious test can be deduced from evaluating all the possible ways $\lambda =(\beta {\minus}1)$ in equation (1) can be negative and is summarized in Table 1. The only way λ can be negative and not spurious is for $\beta \,\lt \,0$ and in this case λ must be less than ${\minus}1$ (first row). If the value of β is such that $0\leq \,\beta \,\lt \,1$ , then the value of λ will be negative and in the range ${\minus}1\,\leq \,\lambda \,\lt 0$ (second row). However, this only occurs because the ${\minus}1$ in λ dominates the positive value of β and so the negative relationship is solely due to the fact that energy density is in the denominator of the definition of price and thus the relationship is spurious. In the final case, if $1\leq \beta $ , then $0\leq \lambda $ (third row) and there is no negative relationship anyway. Because the value of λ is really determined by the value β, whether or not there is a non-spurious (for simplicity, ‘real’) inverse relationship between price and energy density is ultimately determined by the regression of (log) price per gram v. (log) energy density.

Table 1 Spurious negative relationship summary†

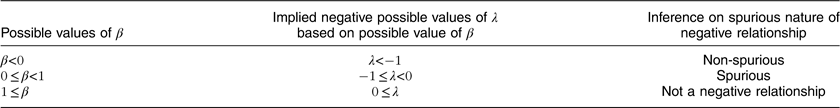
† β is the slope coefficient in the regression model: $\ln p=\alpha {\plus}\beta \ln d{\plus}{\varepsilon}$ , where p is the price of food per gram and d is energy density. λ is the slope coefficient in the regression model: $\ln r=\alpha {\plus}\lambda \ln d{\plus}{\varepsilon}$ , where r is price per energy density and, as discussed in the text, we know $\lambda =(\beta {\minus}1)$ .

Statistical testing framework for spurious correlation

The above logic indicates there are two equivalent ways to test for a spurious inverse relationship between the price per energy density and energy density using a one-sided t test: (i) use the regression equation $\ln r=\alpha {\plus}\lambda \ln d{\plus}{\varepsilon}$ and test

$$H_{0}^{\lambda } :\lambda \geq {\minus}1\,\,\,\,\,\,\,\,\,H_{a}^{\lambda } :\lambda \lt {\minus}1$$

or (ii) use the regression equation $\ln p=\alpha {\plus}\beta \ln d{\plus}{\varepsilon}$ and test

$$H_{0}^{\beta } :\beta \geq 0\,\,\,\,\,\,\,\,\,H_{a}^{\beta } :\beta \,\lt\, 0,$$

where the only difference in the estimating equations is the dependent variable (i.e. $\ln r$ v. $\ln p$ ). Equation (3) is obtained simply by using $\lambda =(\beta {\minus}1)$ in equation (2). It can be shown that the test statistics, and therefore P values, from both tests will be mathematically equivalent. In either case, the null hypothesis is that the relationship between price and energy density is a spurious negative relationship. This should make sense because, as shown in Table 1, the only way for the relationship to not be spurious (be ‘real’) is for $\lambda \lt {\minus}1$ , which is equivalent to $\beta \, \lt \, 0$ , and following standard statistical reasoning, the null hypothesis is the negation of the theoretical hypothesis of interest. If the null hypothesis is rejected in either form, the inverse relationship is deemed statistically non-spurious or simply real. However, if the null hypothesis is not rejected then there cannot be a real inverse relationship, rather the relationship is either a spurious inverse relationship or there is not an inverse relationship. Operationally, the most straightforward approach to determining if a significant inverse relationship is spurious or not is to simply estimate equation (1), note if the estimate of λ is negative, and then ask the software package to conduct the one-sided t test indicated by the null hypothesis in equation (2) and check the P value on this test. Following standard statistical testing procedures, if this P value is greater than a reasonable significance level (e.g. 0·05), the null hypothesis is not rejected and the inverse relationship is spurious; otherwise it is real. Alternatively, if the estimate of λ is non-negative (significant or not) then there is no inverse significant relationship anyway.

Data description

Data from the National Health and Nutrition Examination Survey (NHANES) 2003–04^{( 22 )}, the MyPyramid Equivalent Database 2·0 (MPED)^{( 23 )} and the Center for Nutrition Policy and Promotion’s (CNPP) Food Prices Database 2003–04 (FPD)^{( 24 , 25 )} are utilized in the analysis. The years 2003–04 have the most recent data available for both food prices and cup- and ounce-equivalents.

The NHANES^{( 22 )} is a well-known multistage probability sample of non-institutionalized individuals living in the USA. The 24 h dietary recall data are used to generate a list of foods and calculate the average amount consumed by adults aged 19 years and older who report consuming that food. The 2003–04 sample includes 4578 adult participants with at least one complete dietary recall and for the data used in the present analysis there are 4430 individual foods.

The MPED^{( 23 )} gives the number of cup- and ounce-equivalents in 100 edible grams of each food item. Vegetables, fruits and dairy products are measured in cup-equivalents, and grains and protein foods in ounce-equivalents^{( 26 )}. The MPED does not assign food items into food groups, since many food items have quantities of more than one food group.

US Department of Agriculture’s (USDA) CNPP developed the FPD for all foods reported consumed in the NHANES 2003–04. The database contains estimates of the price per edible 100 g, i.e. the price of the food after it is prepared. The retail price data for the FPD comes from Nielsen’s 2004 Homescan Panel data, a national panel of consumers who record their retail food purchases. Prices are national average prices in $US and include all package sizes and brands that were recorded by panel participants.

Foods were placed in groups following the method outlined by Carlson and Frazao^{( 2 )}. Appendix Tables 11–15 of the Dietary Guidelines for Americans 2010 ^{( 1 )} suggest a standard portion size for vegetables, fruits, dairy, protein foods and grains. If the average amount of the food consumed was at least half of this standard amount, the food was classified into a food group (vegetables, fruit, grain, dairy and protein). The foods were further divided into the same subgroups used in the USDA Food Patterns (see Appendix 7, 8 and 9 of the Dietary Guidelines for Americans 2010 ^{( 1 )}). Of course some foods are a mixture of several food groups. For example, vegetable lasagne purchased at a retail establishment or prepared at home would contain a significant amount of vegetables, dairy and grains. Foods that met the standards for more than one group (say vegetables, dairy and grain) were classified as ‘mixtures’ and where possible were assigned to subgroups, such as vegetable-based mixtures, based on the more predominant group. Two other categories were also created, ‘mixed dishes’ and ‘moderation foods’. The distinction between ‘mixed dishes’ and ‘moderation foods’ is based on the level of saturated fat, added sugars and sodium. ‘Mixed dishes’ foods were allowed at least 4g of saturated fat, 600 mg of Na and 1·25 teaspoons of added sugars. Examples of mixed dishes are items like burritos, casseroles, pizza and soup. ‘Moderation foods’ were defined as any food with at least 480 mg Na, 1 teaspoon of added sugars and/or 3 g of saturated fat. Examples of ‘moderation foods’ are items like a baked potato with bacon and cheese, granola and fruit-flavoured low-fat yoghurt. Foods that did not contain sufficient amounts of any group were classified as ‘non-food group-based foods’. Please see Carlson and Frazao^{( 2 )} for more details on the creation of these groups. In sum, there are twenty-five food groups. All of the following statistical analysis was done using the statistical software package STATA version 11·1.

For each of the twenty-five groups Table 2 shows summary statistics for both the price ($US/100 g) and energy density (4·184 kJ/100 g or equivalent kcal/100 g). All except two groups (Lean Red Meat and Fish) have a price less than $US 1 but, perhaps not surprisingly, there is a greater range of energy densities. The standard deviations within each group indicate a large degree of variability within each group for both price and energy density.

Table 2 Means and standard deviations per 100 g for price and energy density by food group

Results and discussion

Table 3 gives the food groups (column (1)), the estimate of β from the performing regression of the price per gram v. energy density and its P value (columns (2) and (3)), the estimate of λ from the performing the regression of price per energy density v. energy density and its P value (columns (4) and (5)), the P value for the one-sided t test of the null hypothesis that the relationship is spurious (column (6)) and the result of the test (column (7)).

Table 3 Slope estimates and tests results by food group

Highlighted numbers indicate negative relationships that require the test for spurious correlation.

*P<0·05, **P<0·01, ***P<0·001.

† Slope parameter estimate β and P value for H ₀: β=0.

‡ Slope parameter estimate λ and P value for H ₀: λ=0.

§ P value for null hypothesis of spurious correlation (H ₀: λ≥−1) and summary of result.

|| U=unnecessary to conduct spurious test because relationship is not negative and significant.

The relationship $\lambda =(\beta {\minus}1)$ as described above is verified in Table 3. For example, consider the Red Orange Vegetables group (second row). In column (3) β=0·05, but this relationship is not significant (P≥0·05; column (4)). Yet column (4) indicates an inverse relationship as $\lambda ={\minus}0 \!\cdot \!95=(0 \!\cdot\! 05{\minus}1)$ , or for a one unit increase in energy density the log price of Red Orange Vegetable products per energy density will decrease by 0·05 and this relationship is highly significant (P≤0·01; column (5)). However, the P value of 0·75 in column (6) indicates this is a spurious relationship (column (7)). Why? Because this result is achieved solely because the positive $\beta =0 \!\cdot\! 05$ value is dominated by the ${\minus}1$ in the relationship $\lambda =(\beta {\minus}1)$ , and the ${\minus}1$ in this relationship occurs only because energy density is in the denominator of the price definition: units matter.

Of the twenty-five food categories, sixteen show a significant inverse (negative) relationship between price per energy density and energy density (the shaded entries in column (4)), so these need to be checked. Of these sixteen cases, fourteen are spurious based on the spurious test P value (i.e. P≥0·05 in column (5), column (6)). Consequently, there are only two cases where the relationship is non-spurious or real (Poultry, Fish). These two cases could have been alternatively identified by looking for the significant negative estimates of β in column (2). In fact, as mentioned, the value of β is what actually determines the ‘real’ relationship and of the seventeen significant relationships in column (2), fifteen show a positive relationship between energy density, which is just the opposite of that claimed by the ‘real’ proponents, but is consistent with the finding of Lipsky^{( 12 )}. Finally, when all foods are grouped together (last row), there is a significant positive price and energy density relationship in column (2) (0·43) and the negative relationship between the price per energy density and energy density (−0·57; column (4)), while significant, is spurious based on the test (P≥0·05; column (6)).

Conclusions

The purpose of the present communication was to move the literature forward in settling the debate on whether or not higher energy-dense food is cheaper than low energy-dense food. This was accomplished by developing and conducting a statistical test for the null hypothesis that the relationship between price per energy density and energy density is spurious. As with all statistical analysis, the main limitation is the results are particular not universal. Certainly other time periods, locations and foods could yield different results, but the method is universal and can be applied in any data set. The results here suggest that for the majority of cases, the relationship between price and energy density is just the opposite (positive) of that claimed by the ‘real’ proponents (negative). Consequently, the premise in the argument that higher energy-dense foods are purchased because they are cheaper is not substantiated.

Although the results presented here support the position of the ‘spurious’ proponents one should not dismiss the larger contribution made by the ‘real’ proponents: economic factors and nutrition quality are related. However, the relationships are likely more subtle than being portrayed by the ‘real’ proponents and require more sophisticated analysis such as found elsewhere in the literature^{( 27 , 28 )}. The flaw in the economic argument is a flaw in application, not a flaw in economics. The ‘real’ proponents are attempting to couch the explanation of the relationship between income and nutrition quality, and obesity, within the context of a simplistic two-dimensional theory of demand, which is the inappropriate economic framework. There are much more realistic and sophisticated economic models and arguments that need to be utilized and explored.

Economists have long recognized that consumers – and producers – make choices and trade-offs within a multidimensional environment where consumers and producers interact. If there is interest in the relationship between the price of foods and their attributes, as is the case for the ‘real’ proponents, then the more appropriate economic framework is the hedonic model^{( 29 )}. The hedonic model consists of a demand side and a supply side. On the demand side consumers evaluate and choose products based not only on price but also on other attributes of the products and their income and time constraints. Great insights could be gained on the demand side in isolation by conducting choice attribute experiments, such as in Gracia et al.^{( 30 )}. On the supply side, producers (retailers) evaluate and offer products also based on price and attributes as those affect profitability. Consequently the interaction of consumers and producers in the market equilibrium process determines the actual price and product attributes observed in the market. Some of these attributes may be easily observed and measured (e.g. calories, fat content) but others may be more latent, contextual and difficult to measure, such as those considered in the behavioural economics literature (e.g. lighting, background noise or even shape of the food; see Just et al.^{( 31 )} for an overview of such factors). The key point is that the demand (and supply!) for a product will be determined by the collection of attributes, not a single attribute such as energy density.

The work by Brooks et al.^{( 32 )} is the only analysis we are aware of that is more consistent with a hedonic price approach, although they do not mention or reference the hedonic price literature in their article. These authors analyse 106 foods from America and Australia and run a multiple regression analysis of the price per gram v. macronutrient contents. They find that as protein content increased the price of food increased, but as carbohydrate content increased the price of food decreased. While Brooks et al.’s^{( 32 )} analysis is clearly a step in the right direction, there is no real discussion of the supply side of the market, and consequently the policies they recommend should be cautiously evaluated. For example, assuming their biological argument of the protein leveraging hypothesis is correct, incorporating the supply side in the analysis suggests that a tax on energy density, as advocated by the ‘real’ proponents, could actually lead to more overeating. Why? As Barzel^{( 33 )} explains, producers will reallocate inputs so as to minimize the impact of the tax. If carbohydrates are cheaper, as indicated by the hedonic price analysis of Brooks et al.^{( 32 )}, then producers may substitute more carbohydrates in food production while reducing protein content (as carbohydrates and protein have the same caloric value per gram) and thus consumers would have to eat even more food to achieve the protein target. Stated alternatively, the point of Brooks et al.^{( 32 )} is that all calories are not equal. It is the composition of calories that may matter when addressing overeating and satiation, and how producers respond to policies is just as important as to how consumers respond. Clearly, this will require more sophisticated analysis than just looking at the relationship between price and energy density.