Disability-adjusted life years for severe acute malnutrition: implications of alternative model specifications

Abstract

Objective:

Reducing the burden of childhood severe acute malnutrition (SAM) is key to improving global child health outcomes. Assessing cost-effectiveness of nutrition interventions remains an important evidence gap. Disability-adjusted life years (DALYs) are a common indicator used in cost-effectiveness analyses. DALYs were established by the Global Burden of Disease (GBD) study. Recent iterations of the GBD have changed the methods used to calculate DALYs by dropping age-weighting and discounting (AD) and updating disability weights (DW). Cost-effectiveness analyses may use either local or international standard life expectancies (LE). Changes in model specifications for calculating DALYs may have implications for cost-effectiveness analyses using DALYs, interpreting historical DALY estimates, and related resource allocation decisions. The present study aimed to quantify the magnitude of change in estimates of DALYs attributable to SAM given recent methodological changes.

Design:

From secondary data analysis, using parameter values from routine programme monitoring data for two SAM treatment programmes and published literature, eight calculation models were created to estimate DALYs with and without AD, using different sets of DW, and local v. standard LE.

Results:

Different DW had a marginal effect on DALY estimates. Different LE had a small effect when AD was used, but a large effect when AD was not used.

Conclusions:

DALY estimates are sensitive to the model used. This complicates comparisons between studies using different models and needs to be accounted for in decision making. It seems sensible for analyses to report results using models with and without AD and using local and standard LE.

There is growing consensus that reducing the burden of severe acute malnutrition (SAM), or severe wasting, in children is a key component in improving global child nutrition outcomes and child survival⁽¹⁾. Assessing the cost-effectiveness of interventions addressing SAM treatment and prevention remains an important evidence gap⁽²⁾. As part of assessing the effectiveness and cost-effectiveness of interventions addressing SAM, outcomes can be measured using either disease-specific measurements, such as the number of SAM cases that are discharged as cured, or measures that can be applied across all diseases such as disability-adjusted life years (DALYs).

The DALY is a standard metric for disease outcomes that was developed to aid global comparisons in the Global Burden of Disease (GBD) study, an effort initiated by the WHO in 1992 to provide policy makers with a quantitative basis with which to measure disability related to disease and injury^(3–6). The DALY is also an important indicator in comparing the effectiveness and cost-effectiveness of different interventions and the resource investment required in preventing and treating different diseases.

DALY calculations comprise two different estimates: (i) the number of years lived with disability (YLD); and (ii) the number of years of life lost (YLL) associated with the condition of interest. DALYs are estimated as the sum of the YLD and YLL components.

YLD for different diseases are calculated using disease-specific disability weights that range between 0 (perfect health) and 1 (death) and the duration of disability. The disability weight for SAM used in the 2004 GBD study was 0·053⁽⁷⁾. In the 2010 GBD study update, this weight was increased to 0·127 and a separate disability weight was specified for kwashiorkor (0·055)⁽⁸⁾. These disability weights were changed slightly in the 2013 GBD update to 0·128 and 0·051, respectively⁽⁹⁾.

YLL is calculated using estimates of mortality associated with the condition of interest when untreated, life expectancy and age at death. Prior research estimating DALYs attributable to SAM has shown that the largest contribution comes from the YLL component. This is due to the high risk of mortality associated with SAM among young children and the short duration of both treated and untreated SAM disease episodes^(10–13).

Methods differ for DALY calculations used for estimating burden and for estimating cost-effectiveness. When calculating DALYs for cost-effectiveness analysis in a specific context, local life expectancies from local life tables have been used in preference to ‘standard expected years of life lost’ (SEYLL)^(14–16). In contrast, when using DALYs to estimate disease burden, SEYLL is used to avoid inequalities in the weighting of mortality across countries. The 2010 GBD study, for example, used a version of SEYLL with a life expectancy at birth of 86·02 years for males and females and recent estimates from the UN Population Division specify a life expectancy at birth of 91·94 years^(17,18) . Use of SEYLL may have important implications when comparing DALY estimates between studies calculating disease burden and those assessing cost-effectiveness of an intervention in a specific context. This may be a particular problem with SAM and other conditions that are prevalent in societies with much shorter expected life spans than SEYLL.

For the 2010 GBD study, DALY methods were changed to drop the elements of age-weighting and discounting⁽⁸⁾. Age-weighting places more weight on the years of life in early adulthood, with earlier and later years of life given less weight. Discounting places less weight on outcomes that are well into the future than it does to near-term outcomes. The use of age-weighting and discounting has been a long-standing source of controversy^(17,19–21) . Abandoning age-weighting and discounting means that all years of life are given equal weight. This ‘no frills’ approach may present challenges in interpreting historical DALY estimates because older DALY estimates made using age-weighting and discounting may differ substantially from DALY estimates made using the ‘no frills’ approach. This has implications for analysis of cost-effectiveness using DALYs and related decision making for allocation of resources.

Previous studies have assessed effects on DALY estimates of changes in model specifications when estimating disease burden^(22,23) . One cost-effectiveness analysis assessed cost per DALY averted attributable to wasting and stunting by different cash-based preventive interventions using models with local life expectancy, and presented results calculated with and without age-weighting and discounting⁽¹²⁾. To date there has been no published work quantifying the magnitude of the difference in DALY estimates that may be caused by both the use of SEYLL and the abandoning of age-weighting and discounting for conditions such as SAM affecting young children that are associated with high mortality and little or no lasting disability. The objective of the work presented here was to demonstrate the magnitude of change in estimates of DALYs attributable to SAM using different disability weights, local and SEYLL life expectancies, and age-weighting and discounting.

Methods

DALY calculation models were constructed using three binary parameters: (i) with age-weighting and discounting (AD) v. without AD, or ‘no frills’ (NF); (ii) local life expectancies and SEYLL; and (iii) disability weights from GBD 2004 and GBD 2010. These parameters were exhaustively combined giving eight different models:

1. 1. AD; local life expectancy; GBD 2004 disability weights

2. 2. AD; local life expectancy; GBD 2010 disability weights

3. 3. AD; SEYLL; GBD 2004 disability weights

4. 4. AD; SEYLL; GBD 2010 disability weights

5. 5. NF; local life expectancy; GBD 2004 disability weights

6. 6. NF; local life expectancy; GBD 2010 disability weights

7. 7. NF; SEYLL; GBD 2004 disability weights

8. 8. NF; SEYLL; GBD 2010 disability weights

Each of these models was tested by using them to estimate the number of DALYs averted by two programmes: (i) a small (i.e. 724 admissions between June 2009 and June 2010) community-based management of acute malnutrition (CMAM) programme delivered by Save the Children operating in a single health district in Southern Bangladesh⁽²⁴⁾; and (ii) a large (i.e. 919 876 admissions between September 2009 and October 2014) CMAM programme delivered by the Nigerian Ministry of Health supported by UNICEF and operating in eleven states in Northern Nigeria (Adamawa, Bauchi, Borno, Gombe, Jigawa, Kano, Katsina, Kebbi, Sokoto, Yobe and Zamfara states)^(25,26) . The DALY calculation for all models followed the process outlined in the influence diagram/flowchart shown in Fig. 1. DALYs are outcomes which an intervention aims to ‘avert’ or prevent, so we quantify the DALYs associated with any deaths or disability that are expected to have been ‘averted’ or prevented by the intervention.

Fig. 1 Influence diagram/flowchart showing the process for calculating DALYs for all models. *A weighted average (i.e. by case numbers in each category of SAM) disability weight was used. †A weighted (i.e. by numbers of males and females) average of male and female life expectancies was used in YLL calculations for models using local life expectancies; other models used SEYLL (DALY, disability-adjusted life year; SAM, severe acute malnutrition; YLL, years of life lost; SEYLL, standard expected years of life lost; YLD, years lived with disability; MUAC, mid-upper arm circumference; U5MR, under 5 years mortality rate)

The number of cases admitted, the average age at admission, the proportion of cases discharged as cured, the proportion of cases that were female and the average mid-upper arm circumference (MUAC) at admission were taken from routine programme monitoring statistics summarising programme admission and exits^(27,28) . The average length of the untreated SAM disease episode was set to 6 months for all models. This is the average episode length found using three monthly and six monthly follow-up periods reported from Senegal and the Democratic Republic of Congo⁽²⁹⁾. Local male and female life expectancies were taken from local life tables for the period of programme operation⁽³⁰⁾. Standard life expectancies were taken from the ‘Frontier 2050’ SEYLL⁽¹⁸⁾. Expected mortality for untreated SAM cases was estimated using published data on mortality associated with low MUAC in SAM cases in the absence of treatment programmes^(31–35). Using these historical data with cohorts of children of similar age to the children enrolled in the two SAM treatment programmes under analysis and from countries with limited access to health services, we calculated an expected mortality rate for the median admission MUAC in both programmes using linear interpolation^(11,25) . This expected mortality rate was corrected for background mortality estimated from published data on under 5 years mortality rates (U5MR) for the times and places of the historical cohort studies⁽³⁶⁾. To estimate the number of deaths averted, the corrected expected mortality rate was multiplied by the number of cases of SAM successfully recovered by the programmes. Children who died during treatment were assumed to both (i) have not responded to treatment and (ii) for treatment to have contributed no benefit in terms of reduced disability, reduced duration of disability or increased duration of life in the analyses reported here. This method for calculating expected mortality has been described in detail previously^(11,25) . The specific values used for these parameters are shown in Table 1.

Table 1 Parameters values used in each model

MUAC, mid-upper arm circumference; SAM, severe acute malnutrition; SEYLL, standard expected years of life lost.

* From routine programme monitoring and evaluation data.

† Assumed value. Taken from published data⁽²⁹⁾.

‡ From published data (described in text). Local life expectancies are given here. Life expectancy for models using standard life expectancy used the ‘Frontier 2050’ SEYLL, which has a life expectancy at birth of 91·94 years⁽¹⁸⁾.

A sampling-based estimation approach was used, with each parameter modelled by a probability distribution centred upon the best estimate of the parameter with a range reflecting uncertainty^(11,25) . Proportions were modelled using the binomial distribution. The expected number of deaths was modelled using the Poisson distribution. Age at admission and duration of an untreated SAM episode were modelled using the standard gamma distribution. The standard gamma distribution is convenient as ages and durations below 0 are not generated. Disability weights from the GBD 2010 are presented with 95 % uncertainty limits. These were modelled using the continuous uniform distribution with a range defined by the lower and upper 95 % uncertainty limits. Standard YLL and YLD calculations were performed (see Fig. 1). The 50th, 2·5th and 97·5th percentiles of the results provided point estimates and approximate lower and upper 95 % confidence limits, respectively. All models were evaluated using one million replicates. Data were analysed using purpose-written R language (version 3.4.3) scripts managed by the R-Analytic Flow (version 3.1.4) scientific workflow system.

Results

YLL, YLD and DALY estimates for the different models are shown in Table 2. The results show which parameters most strongly influenced DALY estimates. Choice of disability weight was not an important factor in DALY estimates. For acute conditions, like SAM, that are associated with high mortality early in life, DALYs are dominated by the YLL component which comprised more than 99 % of the DALY estimates in all models. Using SEYLL with AD had little effect because YLL far in the future count for little when AD is used. NF had a major effect because YLL far in the future count as much as YLL close in time. SEYLL had a major effect with NF because the extra years (i.e. compared with local life expectancy) contributed a large number of YLL. The combined effect of NF and SEYLL was larger for the Nigeria programme because local life expectancy in Nigeria is lower than in Bangladesh and both are considerably lower than in the SEYLL.

Table 2 YLL, YLD and DALY estimates* for SAM according to the different models using data from Bangladesh and Nigeria

YLL, years of life lost; YLD, years lived with disability; DALY, disability-adjusted life year; SAM, severe acute malnutrition; AD, age-weighting and discounting; NF, age-weighting and discounting not used (‘no frills’); SEYLL, standard expected years of life lost; GBD 2004, disability weights from 2004 GBD; GBD 2010, disability weights from 2010 GBD; GBD, Global Burden of Disease study.

* Intervals (ranges) are expressed in ISO 31-11 form. The form [a, b] expresses the interval a ≤ x ≤ b. For example, [3942, 5528] is used to represent an approximate 95 % CI that ranges between 3942 and 5528.

Using the older model specifications for DALY estimation, with local life expectancy as recommended for cost-effectiveness analysis, along with AD and GBD 2004 disability weights, the models yielded 4717 DALYs averted by the Bangladesh programme and 4 928 765 DALYs averted by the Nigeria programme as shown in Table 2 and in Figs 2 and 3. Changing to an NF approach and updating to GBD 2010 disability weights, while keeping local life expectancy, produced 9064 DALYs averted by the Bangladesh programme and 8 247 507 DALYs averted by the Nigeria programme. The change from old to new model specifications using local life expectancy resulted in an almost 2-fold increase in DALYs (1·9-fold for the Bangladesh programme and 1·7-fold for the Nigeria programme). Changing to an NF model with SEYLL resulted in 12 589 DALYs averted by the Bangladesh programme and 14 088 170 DALYs averted by the Nigeria programme. These results show that changing from the old to the new model specifications used in the 2010 GBD resulted in an almost 3-fold increase in DALY estimates for both countries (2·7-fold for the Bangladesh programme and 2·9-fold for the Nigeria programme). These findings are similar for both programmes despite differences in geographic context, programme scale and local life expectancies.

Fig. 2 DALYs averted by the Bangladesh CMAM programme⁽²⁴⁾ according to the eight calculation models (AD, age-weighting and discounting used; NF, age-weighting and discounting not used (‘no frills’); LOCAL, local life expectancy used for YLL estimates; SEYLL, ‘Frontier 2050’ SEYLL used for YLL estimates⁽¹⁸⁾; 2004, disability weights from 2004 GBD; 2010, disability weights from 2010 GBD); plot shows point estimates with the approximate 95 % CI represented by horizontal bars (DALY, disability-adjusted life year; CMAM, community-based management of acute malnutrition; YLL, years of life lost; SEYLL, standard expected years of life lost; GBD, Global Burden of Disease study)

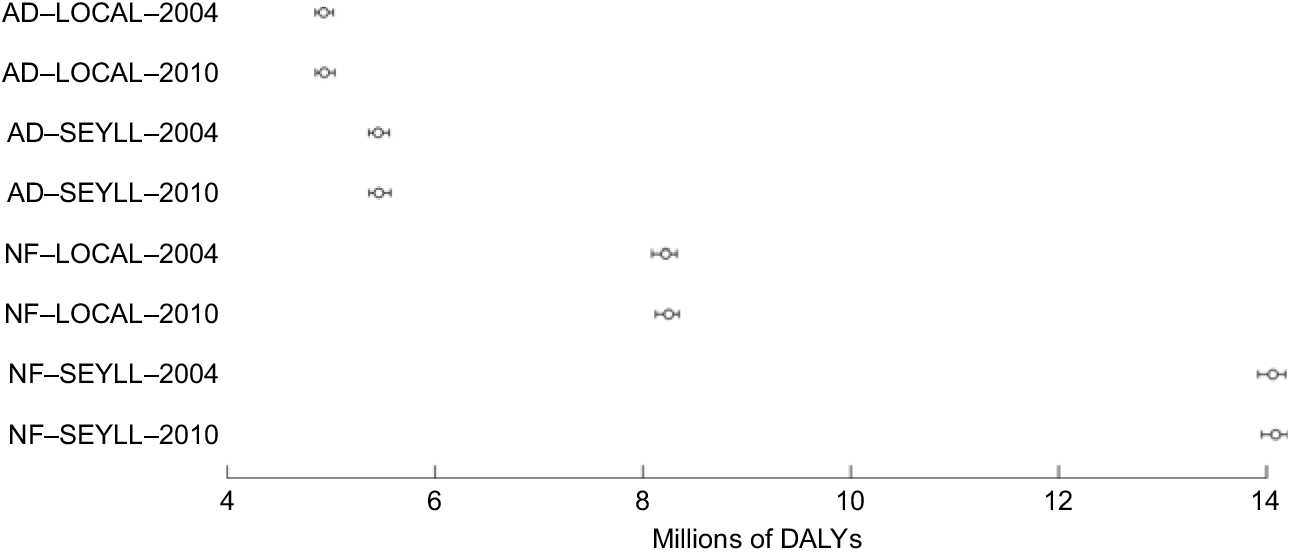
Fig. 3 DALYs averted by the Nigeria CMAM programme^(25,26) according to the eight calculation models (AD, age-weighting and discounting used; NF, age-weighting and discounting not used (‘no frills’); LOCAL, local life expectancy used for YLL estimates; SEYLL, ‘Frontier 2050’ SEYLL used for YLL estimates⁽¹⁸⁾; 2004, disability weights from 2004 GBD; 2010, disability weights from 2010 GBD); plot shows point estimates with the approximate 95 % CI represented by horizontal bars (DALY, disability-adjusted life year; CMAM, community-based management of acute malnutrition; YLL, years of life lost; SEYLL, standard expected years of life lost; GBD, Global Burden of Disease study)

Discussion

The different DALY calculation models can give very different results. Models using AD produce similar results regardless of which expectation of life expectancy or disability weight is used. These models consistently produced lower estimates of DALYs averted than those without AD. Age-weighting places more weight on the years of life in early adulthood. Earlier and later years of life are given less weight. Discounting places less weight on outcomes that are well into the future than it does to near-term outcomes. The combination of age-weighting with discounting means that the extra years of life in later years associated with using SEYLL will make only a small contribution to the YLL component of DALY estimates. For example, a child dying at 2 years of age yields YLL = 35·2 when SEYLL is used, and YLL = 33·7 using the local sex-combined life expectancy for Bangladesh (66·60 years) and YLL = 31·8 using the local sex-combined life expectancy for Nigeria (54·50 years) when AD is used. Inclusion of YLD makes little contribution to the DALY estimate because the duration of the untreated SAM disease episode is short. It is unsurprising that removing AD increased the DALY estimate as many more life years are given higher values. Similar results were found by Devleesschauwer and colleagues⁽²²⁾ who reported a more than twofold increase in DALY estimates when assessing the disease burden attributable to alcohol use disorder when switching from using AD to an NF model when SEYLL was used.

The models using the NF approach and the SEYLL all produce similar results regardless of the disability weight used and produce the highest DALY estimates of all the models. As expected, SEYLL produced higher estimates than local life expectancy because it raises life expectancy far above the local life expectancies in our study settings. Given that SAM disproportionately affects poorer regions, cost-effectiveness analyses for this condition may be particularly affected by these changes to the DALY model.

The models using the NF approach and the local life expectancies produced similar results, with mid-range DALY estimates.

The choice of disability weights had a marginal effect across all models. This would be the same for any acute condition associated with high mortality and no lasting disability but would differ for conditions with high disability weights and/or long durations of illness/disability. For example, in a study in South Africa assessing the disease burden due to epilepsy, a condition associated with one of the highest disability weights in the 2010 GBD study, Wagner and colleagues⁽²³⁾ found that varying the epilepsy-related disability weights from the lowest, due to seizure-free treated epilepsy, to the highest for severe epilepsy resulted in a nearly ninefold increase in estimates of YLD and a 23 % increase in overall DALY estimates.

Alternative model specifications for DALYs attributable to acute malnutrition have been explored in one other study, using data from Pakistan⁽¹²⁾. The results of that study show a similar trend to the present study, despite not being directly comparable with the present analysis due to including DALYs attributable to both moderate and severe acute malnutrition, including a mixture of acute and chronic conditions (i.e. stunting), assessing DALYs averted by a preventive non-clinical intervention and using only local life expectancies. In the analysis from Pakistan, DALY estimates for both wasting and stunting almost doubled when an NF approach with local life expectancies was used, thereby reducing the cost per DALY by one-half compared with DALYs calculated using AD and local life expectancies. Results from the present analysis build on that previous work, showing that adding the use of SEYLL to an NF approach leads to a near tripling of DALY estimates compared with models using local life expectancies with AD.

A change to using the NF model with the SEYLL has the effect of substantially increasing estimates of DALYs averted, therefore decreasing cost per DALY averted, compared with previous work, by nearly threefold for SAM in the contexts analysed here. This may lead to discontinuities in decision making with more interventions being classified as ‘cost-effective’ unless corresponding changes are made to decision rules. This means that models using AD with local life expectancies will probably still need to be used to maintain comparability with previous work and to understand whether changes in DALY estimates and cost per DALY averted are due to changes in disease burden or intervention effectiveness, or to changes in the methods used to calculate DALYs. The next step in calculating the cost per DALY averted by an intervention introduces additional cost variables and related assumptions. Therefore, being clear on variables and assumptions used in calculating DALYs is an important starting point in ensuring transparency of cost-effectiveness estimates.

The present analysis has several limitations. Excess mortality associated with SAM was estimated using a combination of mortality associated with low MUAC found in cohort studies from the 1980s and 1990s corrected using relevant background mortality (see Fig. 1). A common objection against using historical cohorts of untreated SAM cases to estimate excess mortality is the evidence of substantial decreases in childhood mortality since these studies were conducted. This objection is mistaken because the decreases in childhood mortality are due primarily to a combination of reductions in the incidence of the causes of childhood mortality, improvements in treatment coverage and improvements in treatment effectiveness. In our counterfactuals we used the SAM cases admitted to two CMAM programmes and modelled what would happen to these cases if these programmes had not existed. These children already had the disease, so reductions in incidence were not relevant. Cases in the counterfactual were untreated, so improvements in treatment coverage and treatment efficacy were also not relevant. The SAM cases in the counterfactual had the same disease and the same absence of treatment as the SAM cases in the historical cohorts. In the absence of additional and contradictory evidence on the case fatality rates for untreated SAM at different levels of severity (which would now be unethical to collect), there is no good reason to believe that the SAM cases in the counterfactual would not have experienced similar case fatality rates to the SAM cases in the historical cohorts. Background mortality was estimated using the average U5MR reported by the World Bank for the times and places of the cohort studies used to estimate mortality associated with low MUAC. U5MR is not constant over the first 5 years of a child’s life, with most deaths occurring in the first month and first year. Therefore, using U5MR may overestimate background mortality, leading to underestimation of the YLL component of the DALY estimates. It should be noted, however, that U5MR is estimated for whole populations and will likely underestimate mortality in poor and very poor households from which the bulk of SAM cases originate.

The duration of an untreated SAM episode is used to estimate the YLD component of the DALY estimate and has been the subject of recent interest^(37–40). This may be considerably shorter than the average (i.e. 6 months) used in the analysis presented here. Since SAM is an acute condition associated with high mortality and no known lasting disability, the effect of error in specifying the duration of an untreated SAM episode on DALY estimates will be small.

Based on the above-mentioned factors, the DALY estimates presented here are subject to several biases. These were, however, the same for all models. The absolute values of the DALY estimates may lack accuracy but the relative positions of the DALY estimates, which comprise the main results of the analysis, would be unaltered if these biases were reduced or eliminated.

Finally, the analysis presented here is for programmes that used MUAC and bilateral pitting oedema as the sole admission criteria. Some CMAM programmes also admit using weight-for-height. DALY estimates for such programmes may be very different from those reported here because the association between weight-for-height Z-score, severity of wasting and mortality is strongly affected by body shape, which is known to vary between populations^(41,42) . The relative positions of DALY estimates are, however, unlikely to be much different from those presented here.

Conclusions

DALY estimates are sensitive to the model used. SAM is a condition affecting young children, associated with a high mortality and little or no lasting disability. Estimates of DALYs attributable to SAM increased almost threefold when removing AD and using SEYLL. Choice of disability weights had little effect on DALYs attributable to SAM, although this would be different for diseases with higher disability weights and with longer durations of illness and disability. This sensitivity to model specifications complicates comparisons between studies made using different DALY models. This needs to be accounted for when making health policy and planning decisions. It seems sensible for analyses to report results using models with and without AD and using local and SEYLL life expectancies to aid comparisons.