Published online by Cambridge University Press: 01 January 2025
One of the main problems in cluster analysis is that of determining the number of groups in the data. In general, the approach taken depends on the cluster method used. For K-means, some of the most widely employed criteria are formulated in terms of the decomposition of the total point scatter, regarding a two-mode data set of N points in p dimensions, which are optimally arranged into K classes. This paper addresses the formulation of criteria to determine the number of clusters, in the general situation in which the available information for clustering is a one-mode N×N\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$N\times N$$\end{document}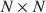 dissimilarity matrix describing the objects. In this framework, p and the coordinates of points are usually unknown, and the application of criteria originally formulated for two-mode data sets is dependent on their possible reformulation in the one-mode situation. The decomposition of the variability of the clustered objects is proposed in terms of the corresponding block-shaped partition of the dissimilarity matrix. Within-block and between-block dispersion values for the partitioned dissimilarity matrix are derived, and variance-based criteria are subsequently formulated in order to determine the number of groups in the data. A Monte Carlo experiment was carried out to study the performance of the proposed criteria. For simulated clustered points in p dimensions, greater efficiency in recovering the number of clusters is obtained when the criteria are calculated from the related Euclidean distances instead of the known two-mode data set, in general, for unequal-sized clusters and for low dimensionality situations. For simulated dissimilarity data sets, the proposed criteria always outperform the results obtained when these criteria are calculated from their original formulation, using dissimilarities instead of distances.
dissimilarity matrix describing the objects. In this framework, p and the coordinates of points are usually unknown, and the application of criteria originally formulated for two-mode data sets is dependent on their possible reformulation in the one-mode situation. The decomposition of the variability of the clustered objects is proposed in terms of the corresponding block-shaped partition of the dissimilarity matrix. Within-block and between-block dispersion values for the partitioned dissimilarity matrix are derived, and variance-based criteria are subsequently formulated in order to determine the number of groups in the data. A Monte Carlo experiment was carried out to study the performance of the proposed criteria. For simulated clustered points in p dimensions, greater efficiency in recovering the number of clusters is obtained when the criteria are calculated from the related Euclidean distances instead of the known two-mode data set, in general, for unequal-sized clusters and for low dimensionality situations. For simulated dissimilarity data sets, the proposed criteria always outperform the results obtained when these criteria are calculated from their original formulation, using dissimilarities instead of distances.