Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Garali, Imene
Adanyeguh, Isaac M
Ichou, Farid
Perlbarg, Vincent
Seyer, Alexandre
Colsch, Benoit
Moszer, Ivan
Guillemot, Vincent
Durr, Alexandra
Mochel, Fanny
and
Tenenhaus, Arthur
2018.
A strategy for multimodal data integration: application to biomarkers identification in spinocerebellar ataxia.
Briefings in Bioinformatics,
Vol. 19,
Issue. 6,
p.
1356.
Vilor-Tejedor, Natàlia
Alemany, Silvia
Cáceres, Alejandro
Bustamante, Mariona
Pujol, Jesús
Sunyer, Jordi
and
González, Juan R.
2018.
Strategies for integrated analysis in imaging genetics studies.
Neuroscience & Biobehavioral Reviews,
Vol. 93,
Issue. ,
p.
57.
Bougeard, Stéphanie
Niang, Ndèye
Verron, Thomas
and
Bry, Xavier
2018.
Current multiblock methods: Competition or complementarity? A comparative study in a unified framework.
Chemometrics and Intelligent Laboratory Systems,
Vol. 182,
Issue. ,
p.
131.
Jun, Inyoung
Choi, Wooree
and
Park, Mira
2018.
Multi-block Analysis of Genomic Data Using Generalized Canonical Correlation Analysis.
Genomics & Informatics,
Vol. 16,
Issue. 4,
p.
e33.
Karkar, S.
Gloaguen, A.
Le Guen, Y.
Pierre-Jean, M.
Dandine-Roulland, C.
Le Floch, E.
Philippe, C.
Tenenhaus, A.
and
Frouin, V.
2019.
Multivariate Haplotype Analysis Of 96 Sulci Opening For 15,612 UK-Biobank Sujects.
p.
392.
Min, Eun Jeong
Safo, Sandra E
Long, Qi
and
Stegle, Oliver
2019.
Penalized co-inertia analysis with applications to -omics data.
Bioinformatics,
Vol. 35,
Issue. 6,
p.
1018.
Guigui, N.
Philippe, C.
Gloaguen, A.
Karkar, S.
Guillemot, V.
Lofstedt, T.
and
Frouin, V.
2019.
Network Regularization in Imaging Genetics Improves Prediction Performances and Model Interpretability on Alzheimer’s Disease.
p.
1403.
Smolinska, Agnieszka
Engel, Jasper
Szymanska, Ewa
Buydens, Lutgarde
and
Blanchet, Lionel
2019.
Data Fusion Methodology and Applications.
Vol. 31,
Issue. ,
p.
51.
Wozniak, Jacob M.
Mills, Robert H.
Olson, Joshua
Caldera, J.R.
Sepich-Poore, Gregory D.
Carrillo-Terrazas, Marvic
Tsai, Chih-Ming
Vargas, Fernando
Knight, Rob
Dorrestein, Pieter C.
Liu, George Y.
Nizet, Victor
Sakoulas, George
Rose, Warren
and
Gonzalez, David J.
2020.
Mortality Risk Profiling of Staphylococcus aureus Bacteremia by Multi-omic Serum Analysis Reveals Early Predictive and Pathogenic Signatures.
Cell,
Vol. 182,
Issue. 5,
p.
1311.
Xia, Yinglin
2020.
The Microbiome in Health and Disease.
Vol. 171,
Issue. ,
p.
309.
Górecki, Tomasz
Krzyśko, Mirosław
and
Wołyński, Waldemar
2020.
Generalized canonical correlation analysis for functional data.
Biometrical Letters,
Vol. 57,
Issue. 1,
p.
1.
Fan, Ziling
Zhou, Yuan
and
Ressom, Habtom W.
2020.
MOTA: Network-Based Multi-Omic Data Integration for Biomarker Discovery.
Metabolites,
Vol. 10,
Issue. 4,
p.
144.
Leung, Marcus H. Y.
Tong, Xinzhao
Bastien, Philippe
Guinot, Florent
Tenenhaus, Arthur
Appenzeller, Brice M. R.
Betts, Richard J.
Mezzache, Sakina
Li, Jing
Bourokba, Nasrine
Breton, Lionel
Clavaud, Cécile
and
Lee, Patrick K. H.
2020.
Changes of the human skin microbiota upon chronic exposure to polycyclic aromatic hydrocarbon pollutants.
Microbiome,
Vol. 8,
Issue. 1,
Hwang, Heungsun
and
Cho, Gyeongcheol
2020.
Global Least Squares Path Modeling: A Full-Information Alternative to Partial Least Squares Path Modeling.
Psychometrika,
Vol. 85,
Issue. 4,
p.
947.
Min, Eun Jeong
and
Long, Qi
2020.
Sparse multiple co-Inertia analysis with application to integrative analysis of multi -Omics data.
BMC Bioinformatics,
Vol. 21,
Issue. 1,
Varghese, Rency S.
Zhou, Yuan
Barefoot, Megan
Chen, Yifan
Di Poto, Cristina
Balla, Abdalla Kara
Oliver, Everett
Sherif, Zaki A.
Kumar, Deepak
Kroemer, Alexander H.
Tadesse, Mahlet G.
and
Ressom, Habtom W.
2020.
Identification of miRNA-mRNA associations in hepatocellular carcinoma using hierarchical integrative model.
BMC Medical Genomics,
Vol. 13,
Issue. 1,
Tanabe, Kazuhiro
Hayashi, Chihiro
Katahira, Tomoko
Sasaki, Katsuhiko
and
Igami, Ko
2021.
Multiblock metabolomics: An approach to elucidate whole-body metabolism with multiblock principal component analysis.
Computational and Structural Biotechnology Journal,
Vol. 19,
Issue. ,
p.
1956.
Cantini, Laura
Zakeri, Pooya
Hernandez, Celine
Naldi, Aurelien
Thieffry, Denis
Remy, Elisabeth
and
Baudot, Anaïs
2021.
Benchmarking joint multi-omics dimensionality reduction approaches for the study of cancer.
Nature Communications,
Vol. 12,
Issue. 1,
Rebei, Amine
Alentorn, Agusti
Chegraoui, Hamza
Frouin, Vincent
and
Philippe, Cathy
2021.
Contribution Of Imaging-Genetics To Overall Survival Prediction Compared To Clinical Status For Pcnsl Patients.
p.
832.
Revilla, Lluís
Mayorgas, Aida
Corraliza, Ana M.
Masamunt, Maria C.
Metwaly, Amira
Haller, Dirk
Tristán, Eva
Carrasco, Anna
Esteve, Maria
Panés, Julian
Ricart, Elena
Lozano, Juan J.
Salas, Azucena
and
Carbonero, Franck
2021.
Multi-omic modelling of inflammatory bowel disease with regularized canonical correlation analysis.
PLOS ONE,
Vol. 16,
Issue. 2,
p.
e0246367.
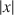 , x2\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$x^{2}$$\end{document}
, x2\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$x^{2}$$\end{document}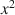 or x4\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$x^{4}$$\end{document}
or x4\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$x^{4}$$\end{document}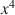 and shrinkage constants 0 or 1, many multiblock component methods are recovered.
and shrinkage constants 0 or 1, many multiblock component methods are recovered.

