Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-07T16:23:43.435Z Has data issue: false hasContentIssue false
  • English
  • Français

Power Divergence Family of Statistics for Person Parameters in IRT Models

Published online by Cambridge University Press:  01 January 2025

Xiang Liu Open the ORCID record for Xiang Liu [Opens in a new window] ,
James Yang ,
Hui Soo Chae  and
Gary Natriello
Xiang Liu*
Affiliation:
Columbia University Educational Testing Service
James Yang
Affiliation:
Columbia University
Hui Soo Chae
Affiliation:
Columbia University
Gary Natriello
Affiliation:
Columbia University
*
Correspondence should be made to Xiang Liu, Educational Testing Service, 03-T, 660 Rosedale Road, Princeton, NJ08541, USA. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We generalize the power divergence (PD) family of statistics to the two-parameter logistic IRT model for the purpose of constructing hypothesis tests and confidence intervals of the person parameter. The well-known score test statistic is a special case of the proposed PD family. We also prove the proposed PD statistics are asymptotically equivalent and converge in distribution to χ12\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\chi _{1}^2$$\end{document}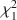. In addition, a moment matching method is introduced to compare statistics and choose the optimal one within the PD family. Simulation results suggest that the coverage rate of the associated confidence interval is well controlled even under small sample sizes for some PD statistics. Compared to some other approaches, the associated confidence intervals exhibit smaller lengths while maintaining adequate coverage rates. The utilities of the proposed method are demonstrated by analyzing a real data set.

Keywords

power divergence familyIRTsufficient statisticsasymptotic distributioninterval estimation
Type
Theory and Methods
Information
Psychometrika , Volume 85 , Issue 2 , June 2020 , pp. 502 - 525
Copyright
Copyright © 2020 The Psychometric Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Xiang Liu and James Yang have contributed equally.

References

Agresti, A. (2003). Dealing with discreteness: Making ‘exact’ confidence intervals for proportions, differences of proportions, and odds ratios more exact. Statistical Methods in Medical Research, 12 (1), 3– 21. CrossRefGoogle ScholarPubMed
Agresti, A. (2011). Score and pseudo-score confidence intervals for categorical data analysis. London: Taylor & Francis. CrossRefGoogle Scholar
Baker, FB Kim, SH (2004). Item response theory: Parameter estimation techniques 2, Boca Raton, FL: CRC Press. CrossRefGoogle Scholar
Basu, A., Shioya, H., & Park, C. (2011). Statistical inference: The minimum distance approach. London: Taylor & Francis. CrossRefGoogle Scholar
Biehler, M., Holling, H., & Doebler, P. (2014). Saddlepoint approximations of the distribution of the person parameter in the two parameter logistic model. Psychometrika, 80 (3), 665– 688. CrossRefGoogle ScholarPubMed
Casella, G., & Berger, R. (2001). Statistical inference. New York: Duxbury Resource Center. Textbook Binding. Google Scholar
Cressie, N. (1984). Multinomial goodness-of-fit tests. Journal of the Royal Statistical Society. Series B (Methodological), 46 (3), 440– 464. CrossRefGoogle Scholar
Doebler, A., Doebler, P., & Holling, H. (2012). Optimal and most exact confidence intervals for person parameters in item response theory models. Psychometrika, 78 (1), 98– 115. CrossRefGoogle ScholarPubMed
Drasgow, F., Levine, M. V., & Williams, E. A. (1985). Appropriateness measurement with polychotomous item response models and standardized indices. British Journal of Mathematical and Statistical Psychology, CrossRefGoogle Scholar
Felipe, A., Miranda, P., & Pardo, L. Minimum Φ \documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$\Phi $$\end{document} -divergence estimation in constrained latent class models for binary data (2015). Psychometrika, Google Scholar
Hambleton, R. K., & Swaminathan, H. (1985). Item response theory: Principles and applications. Boston: Kluwer-Nijhoff Publishing. 10.1007/978-94-017-1988-9 CrossRefGoogle Scholar
Harel, D. (2014). The effect of model misspecification for polytomous logistic adjacent category item response theory models. Unpublished doctoral dissertation. Montreal, QC: McGill University.Google Scholar
Jin, S., Thulin, M., & Larsson, R. (2017). Approximate bayesianity of frequentist confidence intervals for a binomial proportion. American Statistician, 71 (2), 106– 111. CrossRefGoogle Scholar
Klauer, K. C. (1991). Exact and best confidence intervals for the ability parameter of the Rasch model. Psychometrika, 56 (3), 535– 547. CrossRefGoogle Scholar
Liu, X., Han, Z., & Johnson, M. S. (2018). The UMP exact test and the confidence interval for person parameters in IRT models. Psychometrika, 83 (1), 182– 202. CrossRefGoogle ScholarPubMed
Liu, Y., Hannig, J., Pal Majumder, A. (2019). Second-order probability matching priors for the person parameter in unidimensional IRT models. Psychometrika, 84 (3), 701– 718. CrossRefGoogle ScholarPubMed
Liu, Y., Yang, J. S. (2018). Bootstrap-calibrated interval estimates for latent variable scores in item response theory. Psychometrika, 83 (2), 333– 354. CrossRefGoogle ScholarPubMed
Lord, F. M. (1983). Unbiased estimators of ability parameters, of their variance, and of their parallel-forms reliability. Psychometrika, 48 (2), 233– 245. CrossRefGoogle Scholar
Lugannani, R., & Rice, S. (1980). Saddle point approximation for the distribution of the sum of independent random variables. Advances in Applied Probability. https://doi.org/10.1017/s0001867800050278.CrossRefGoogle Scholar
Meijer, R. R., & Sijtsma, K. (2001). Methodology review: Evaluating person fit. Applied Psychological Measurement. https://doi.org/10.1177/01466210122031957.CrossRefGoogle Scholar
Morimoto, T. (1963). Markov processes and the H-theorem. Journal of the Physical Society of Japan, 10.1143/JPSJ.18.328 CrossRefGoogle Scholar
Ogasawara, H. (2012). Asymptotic expansions for the ability estimator in item response theory. Computational Statistics, 27 (4), 661– 683. CrossRefGoogle Scholar
Ogasawara, H. (2013). Asymptotic properties of the Bayes and pseudo Bayes estimators of ability in item response theory. Journal of Multivariate Analysis, 114, 359– 377. CrossRefGoogle Scholar
Ogasawara, H. (2019). 2019 Asymptotic cumulants of the minimum phi-divergence estimator for categorical data under possible model misspecification. Communications in Statistics—Theory and Methods. https://doi.org/10.1080/03610926.2019.1576888.CrossRefGoogle Scholar
Rizopoulos, D. (2015). ltm: An R package for latent variable modeling and item response theory analyses. Journal of Statistical Software, 17 (5), 1– 25. Google Scholar
Sinharay, S. (2016). Asymptotically correct standardization of person-fit statistics beyond dichotomous items. Psychometrika, 81 (4), 992– 1013. CrossRefGoogle ScholarPubMed
Snijders, T. A. B. (2001). Asymptotic null distribution of person fit statistics with estimated person parameter. Psychometrika, 66 (3), 331– 342. CrossRefGoogle Scholar
Warm, T. A. (1989). Weighted likelihood estimation of ability in item response theory. Psychometrika, 54 (3), 427– 450. CrossRefGoogle Scholar