Article contents
A Note on the Asymptotic Distribution of the Greatest Lower Bound to Reliability
Published online by Cambridge University Press: 01 January 2025
Extract
In a recent article Bentler and Woodward (1983) discussed computational and statistical issues related to the greatest lower bound ρ+ to reliability. Although my work (Shapiro, 1982) was cited frequently some results presented were misunderstood. A sample estimate 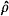 + of ρ + was considered and it was claimed (Bentler & Woodward) that: “Since
+ of ρ + was considered and it was claimed (Bentler & Woodward) that: “Since 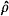 + is not a closed form expression ... an exact analytic expression for h has not been found” (p. 247). (h is a vector of partial derivatives of ρ+ as a function of the covariance matrix.) Therefore Bentler and Woodward proposed to use numerical derivatives in order to evaluate the asymptotic variance avar (
+ is not a closed form expression ... an exact analytic expression for h has not been found” (p. 247). (h is a vector of partial derivatives of ρ+ as a function of the covariance matrix.) Therefore Bentler and Woodward proposed to use numerical derivatives in order to evaluate the asymptotic variance avar ( 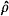 +) of
+) of 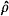 +.
+.
- Type
- Notes And Comments
- Information
- Copyright
- Copyright © 1985 The Psychometric Society
References
- 1
- Cited by


