Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-08T12:02:56.617Z Has data issue: false hasContentIssue false
  • English
  • Français

Inferring the Number of Attributes for the Exploratory DINA Model

Published online by Cambridge University Press:  01 January 2025

Yinghan Chen ,
Ying Liu ,
Steven Andrew Culpepper Open the ORCID record for Steven Andrew Culpepper [Opens in a new window]  and
Yuguo Chen Open the ORCID record for Yuguo Chen [Opens in a new window]
Yinghan Chen
Affiliation:
University of Nevada, Reno
Ying Liu
Affiliation:
University of Illinois at Urbana-Champaign
Steven Andrew Culpepper*
Affiliation:
University of Illinois at Urbana-Champaign
Yuguo Chen
Affiliation:
University of Illinois at Urbana-Champaign
*
Correspondence should be made to Steven Andrew Culpepper, Department of Statistics, University of Illinois at Urbana-Champaign, 725 South Wright Street, Champaign, IL 61820, USA. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Diagnostic classification models (DCMs) are widely used for providing fine-grained classification of a multidimensional collection of discrete attributes. The application of DCMs requires the specification of the latent structure in what is known as the Q\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$${\varvec{Q}}$$\end{document}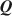 matrix. Expert-specified Q\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$${\varvec{Q}}$$\end{document} 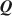matrices might be biased and result in incorrect diagnostic classifications, so a critical issue is developing methods to estimate Q\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$${\varvec{Q}}$$\end{document} 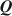in order to infer the relationship between latent attributes and items. Existing exploratory methods for estimating Q\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$${\varvec{Q}}$$\end{document} 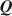must pre-specify the number of attributes, K. We present a Bayesian framework to jointly infer the number of attributes K and the elements of Q\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$${\varvec{Q}}$$\end{document}. We propose the crimp sampling algorithm to transit between different dimensions of K and estimate the underlying Q\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$${\varvec{Q}}$$\end{document}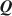 and model parameters while enforcing model identifiability constraints. We also adapt the Indian buffet process and reversible-jump Markov chain Monte Carlo methods to estimate Q\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$${\varvec{Q}}$$\end{document}. We report evidence that the crimp sampler performs the best among the three methods. We apply the developed methodology to two data sets and discuss the implications of the findings for future research.

Keywords

diagnostic modelsdimensionalityDirichlet processesIndian buffet processreversible jump MCMCBayesian
Type
Theory and Methods
Information
Psychometrika , Volume 86 , Issue 1 , March 2021 , pp. 30 - 64
Copyright
Copyright © 2021 The Psychometric Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Brooks, S. P., Gelman, A. (1998). General methods for monitoring convergence of iterative simulations. Journal of Computational and Graphical Statistics, 7(4), 434–455.CrossRefGoogle Scholar
Chen, Y., Culpepper, S., & Liang, F. (2020).A sparse latent class model for cognitive diagnosis. Psychometrika, 85 121–153.CrossRefGoogle ScholarPubMed
Chen, Y., Culpepper, S., & Liang, F. (2020b). A sparse latent class model for cognitive diagnosis. Psychometrika, 1–33.CrossRefGoogle Scholar
Chen, Y., Culpepper, S. A., Chen, Y., & Douglas, J. (2018). Bayesian estimation of the DINA Q. Psychometrika, 83(1), 89–108.CrossRefGoogle ScholarPubMed
Chen, Y., Culpepper, S. A., Wang, S., & Douglas, J. A. (2018). A hidden Markov model for learning trajectories in cognitive diagnosis with application to spatial rotation skills. Applied Psychological Measurement,42, 5–23.CrossRefGoogle ScholarPubMed
Chen, Y., Liu, J., Xu, G., & Ying, Z. (2015). Statistical analysis of Q-matrix based diagnostic classification models. Journal of the American Statistical Association, 110 (510), 850–866.CrossRefGoogle Scholar
Culpepper, S. A. (2015). Bayesian estimation of the DINA model with Gibbs sampling. Journal of Educational and Behavioral Statistics, 40 (5), 454–476.CrossRefGoogle Scholar
Culpepper, S. A. (2019a). Estimating the cognitive diagnosis Q matrix with expert knowledge: Application to the fraction-subtraction dataset. Psychometrika, 84 (2), 333–357.CrossRefGoogle Scholar
Culpepper, S. A. (2019b). An exploratory diagnostic model for ordinal responses with binary attributes: Identifiability and estimation. Psychometrika, 84 (4), 921–940.CrossRefGoogle ScholarPubMed
Culpepper, S. A., & Chen, Y. (2018). Development and application of an exploratory reduced reparameterized unified model. Journal of Educational and Behavioral Statistics, 44 3–24.CrossRefGoogle Scholar
de la Torre, J. (2011). The generalized DINA model framework. Psychometrika, 76 (2), 179–199.CrossRefGoogle Scholar
de la Torre, J., & Douglas, J. A. (2004). Higher-order latent trait models for cognitive diagnosis. Psychometrika, 69 (3), 333–353.CrossRefGoogle Scholar
de la Torre, J., & Douglas, J. A. (2008). Model evaluation and multiple strategies in cognitive diagnosis: An analysis of fraction subtraction data. Psychometrika, 73 (4), 595–624.CrossRefGoogle Scholar
Doshi-Velez, F., & Williamson, S. A. (2017). Restricted Indian buffet processes. Statistics and Computing, 27 (5), 1205–1223.CrossRefGoogle Scholar
Fang, G., Liu, J., & Ying, Z. (2019). On the identifiability of diagnostic classification models. Psychometrika, 84 (1), 19–40.CrossRefGoogle ScholarPubMed
Gershman, S. J., & Blei, D. M. (2012). A tutorial on Bayesian nonparametric models. Journal of Mathematical Psychology, 56 (1), 1–12.CrossRefGoogle Scholar
Green, P. J. (1995). Reversible jump Markov chain Monte Carlo computation and Bayesian model determination. Biometrika, 82 (4), 711–732.CrossRefGoogle Scholar
Griffiths, T. L., & Ghahramani, Z. (2005). Infinite latent feature models and the Indian buffet process (Technical Report 2005-001). London: Gatsby Computational Neuroscience Unit.Google Scholar
Griffiths, T. L., & Ghahramani, Z. (2011). The Indian buffet process: An introduction and review. Journal of Machine Learning Research, 12Apr,1185–1224.Google Scholar
Gu, Y., & Xu, G. (2019). The sufficient and necessary condition for the identifiability and estimability of the dina model. Psychometrika, 84 (2), 468–483.CrossRefGoogle ScholarPubMed
Gu, Y., & Xu, G. (in press). Sufficient and necessary conditions for the identifiability of the Q-matrix. Statistica Sinica. https://doi.org/10.5705/ss.202018.0410CrossRefGoogle Scholar
Heller, J., & Wickelmaier, F. (2013). Minimum discrepancy estimation in probabilistic knowledge structures. Electronic Notes in Discrete Mathematics, 42, 49–56.CrossRefGoogle Scholar
Henson, R. A., Templin, J. L., & Willse, J. T. (2009). Defining a family of cognitive diagnosis models using log-linear models with latent variables. Psychometrika, 74 (2), 191–210.CrossRefGoogle Scholar
Kaya, Y., & Leite, W. L. (2017). Assessing change in latent skills across time with longitudinal cognitive diagnosis modeling: An evaluation of model performance. Educational and Psychological Measurement, 77 (3), 369–388.CrossRefGoogle ScholarPubMed
Li, F., Cohen, A., Bottge, B., & Templin, J. (2016). A latent transition analysis model for assessing change in cognitive skills. Educational and Psychological Measurement, 76 (2), 181–204.CrossRefGoogle ScholarPubMed
Liu, C. -W., Andersson, B., & Skrondal, A. (2020). A constrained metropolis-hastings robbins-monro algorithm for q matrix estimation in dina models. Psychometrika, 85 (2), 322–357.CrossRefGoogle ScholarPubMed
Liu, J., Xu, G., & Ying, Z. (2013). Theory of the self-learning Q-matrix. Bernoulli, 19(5A), 1790–1817.CrossRefGoogle ScholarPubMed
Liu, J. S. (1994). The collapsed Gibbs sampler in Bayesian computations with applications to a gene regulation problem. Journal of the American Statistical Association, 89 (427), 958–966.CrossRefGoogle Scholar
Madison, M. J., & Bradshaw, L. P. (2018). Assessing growth in a diagnostic classification model framework. Psychometrika, 83, 963–990.CrossRefGoogle Scholar
Sen, S., & Bradshaw, L. (2017). Comparison of relative fit indices for diagnostic model selection. Applied Psychological Measurement, 41 (6), 422–438.CrossRefGoogle ScholarPubMed
Sethuraman, J. (1994). A constructive definition of Dirichlet priors. Statistica Sinica, 4, 639–650.Google Scholar
Sorrel, M. A., Olea, J., Abad, F. J., de la Torre, J., Aguado, D., & Lievens, F. (2016). Validity and reliability of situational judgement test scores: A new approach based on cognitive diagnosis models. Organizational Research Methods, 19 (3), 506–532.CrossRefGoogle Scholar
Tatsuoka, C. (2002). Data analytic methods for latent partially ordered classification models. Journal of the Royal Statistical Society: Series C (Applied Statistics), 51 (3), 337–350.Google Scholar
Tatsuoka, K. K. (1984). Analysis of errors in fraction addition and subtraction problems. Computer-Based Education Research Laboratory: University of Illinois at Urbana-Champaign.Google Scholar
Teh, Y. W., Grür, D., & Ghahramani, Z. (2007). Stick-breaking construction for the Indian buffet process. In Artificial intelligence and statistics (pp. 556–563). San Juan, Puerto Rico.Google Scholar
Thibaux, R., & Jordan, M. I. (2007). Hierarchical beta processes and the Indian buffet process. In Artificial intelligence and statistics (pp. 564–571). San Juan, Puerto Rico.Google Scholar
von Davier, M. (2008). A general diagnostic model applied to language testing data. British Journal of Mathematical and Statistical Psychology, 61 (2), 287–307.CrossRefGoogle ScholarPubMed
Wang, S., Yang, Y., Culpepper, S. A., & Douglas, J. (2017). Tracking skill acquisition with cognitive diagnosis models: A higher-order hidden Markov model with covariates. Journal of Educational and Behavioral Statistics, 43 (1), 57–87.CrossRefGoogle Scholar
Wang, S., Zhang, S., Douglas, J., & Culpepper, S. A. (2018). Using response times to assess learning progress: A joint model for responses and response times. Measurement: Interdisciplinary Research and Perspectives, 16 (1), 45–58.Google Scholar
Xu, G. (2017). Identifiability of restricted latent class models with binary responses. Annals of Statistics, 45 (2), 675–707.CrossRefGoogle Scholar
Xu, G., & Shang, Z. (2018). Identifying latent structures in restricted latent class models. Journal of the American Statistical Association, 113 (523), 1284–1295.CrossRefGoogle Scholar
Xu, G., & Zhang, S. (2016). Identifiability of diagnostic classification models. Psychometrika, 81 (3), 625–649.CrossRefGoogle ScholarPubMed
Ye, S., Fellouris, G., Culpepper, S. A., & Douglas, J. (2016). Sequential detection of learning in cognitive diagnosis. British Journal of Mathematical and Statistical Psychology, 69 (2), 139–158.CrossRefGoogle ScholarPubMed
Zhang, S., Douglas, J., Wang, S., & Culpepper, S. A. (in press). Reduced reparameterized unified model applied to learning spatial reasoning skills. In M. von Davier & Y. Lee (Eds.), Handbook of diagnostic classification models. New York: Springer.Google Scholar